\(\)
Problem 9-2
Explain why the charge density corresponding to a single charge \(e\) located at the point \(\mathbf{x}(t)=(x(t),y(t),z(t))\) at time \(t\) is
\begin{equation}
\def\mb#1{\mathbf{#1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\rho(\mb{r},t)=e\,\delta\{ r_x-x(t)\} \,\delta\{r_y-y(t)\}\,\delta\{r_z-z(t)\}=e\,\delta^{3}\{\mb{r}-\mb{x}(t)\}
\tag{1}
\end{equation}
\def\mb#1{\mathbf{#1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\rho(\mb{r},t)=e\,\delta\{ r_x-x(t)\} \,\delta\{r_y-y(t)\}\,\delta\{r_z-z(t)\}=e\,\delta^{3}\{\mb{r}-\mb{x}(t)\}
\tag{1}
\end{equation}
Show that
\begin{equation}
\rho_{\mb{k}}(t)=e\,e^{-i\mb{k}\cdot\mb{x}(t)}
\tag{9-15}
\end{equation}
\rho_{\mb{k}}(t)=e\,e^{-i\mb{k}\cdot\mb{x}(t)}
\tag{9-15}
\end{equation}
Explain why the currrent density is
\begin{equation}
\mb{j}(\mb{r},t)=e\,\dot{\mb{x}}(t)\,\delta^{3}\{\mb{r}-\mb{x}(t)\}
\tag{2}
\end{equation}
\mb{j}(\mb{r},t)=e\,\dot{\mb{x}}(t)\,\delta^{3}\{\mb{r}-\mb{x}(t)\}
\tag{2}
\end{equation}
If we have a number of charges \(e_i\) located at \(\mb{x}_i(t)\), the values of \(\rho_{\mb{k}}\) and \(\mb{j}_{\mb{k}}\) are
\begin{equation}
\rho_{\mb{k}}=\sum_i e_i\,e^{-i\mb{k}\cdot\mb{x}_i(t)},\qquad \mb{j}_{\mb{k}}=\sum_i e_i\,\dot{\mb{x}}_i(t)\,e^{-i\mb{k}\cdot\mb{x}_i(t)}
\tag{9-16}
\end{equation}
\rho_{\mb{k}}=\sum_i e_i\,e^{-i\mb{k}\cdot\mb{x}_i(t)},\qquad \mb{j}_{\mb{k}}=\sum_i e_i\,\dot{\mb{x}}_i(t)\,e^{-i\mb{k}\cdot\mb{x}_i(t)}
\tag{9-16}
\end{equation}
If the expansions of \(\mb{E}\) and \(\mb{B}\) are
\begin{equation}
\mb{E}(\mb{r},t)=\int \mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\frac{d^{3}\mb{k}}{(2\pi)^{3}},\qquad
\mb{B}(\mb{r},t)=\int \mb{B}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\frac{d^{3}\mb{k}}{(2\pi)^{3}}
\tag{3}
\end{equation}
\mb{E}(\mb{r},t)=\int \mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\frac{d^{3}\mb{k}}{(2\pi)^{3}},\qquad
\mb{B}(\mb{r},t)=\int \mb{B}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\frac{d^{3}\mb{k}}{(2\pi)^{3}}
\tag{3}
\end{equation}
then, using Eqs. (9-9) and (9-7), the expansion coefficients satisfy
\begin{equation}
\mb{E}_{\mb{k}}=-i\,\mb{k}\,\phi_{\mb{k}}-\sqrt{4\pi}\,\dot{\mb{a}}_{\mb{k}},\quad\mathrm{and}\quad
\mb{B}_{\mb{k}}=\sqrt{4\pi}\,c\, i\,(\mb{k}\times\mb{a}_{\mb{k}})
\tag{4}
\end{equation}
\mb{E}_{\mb{k}}=-i\,\mb{k}\,\phi_{\mb{k}}-\sqrt{4\pi}\,\dot{\mb{a}}_{\mb{k}},\quad\mathrm{and}\quad
\mb{B}_{\mb{k}}=\sqrt{4\pi}\,c\, i\,(\mb{k}\times\mb{a}_{\mb{k}})
\tag{4}
\end{equation}
From Eqs. (9-8) and (9-10), the coefficient of expansion of \(\nabla\times\mb{E}\) is
\begin{equation}
i\mb{k}\cdot\mb{E}_{\mb{k}}=k^{2}\phi_{\mb{k}}
\tag{5}
\end{equation}
i\mb{k}\cdot\mb{E}_{\mb{k}}=k^{2}\phi_{\mb{k}}
\tag{5}
\end{equation}
so we have
\begin{equation}
k^{2}\phi_{\mb{k}} = 4\pi \rho_{\mb{k}}
\tag{9-17}
\end{equation}
k^{2}\phi_{\mb{k}} = 4\pi \rho_{\mb{k}}
\tag{9-17}
\end{equation}
or,
\begin{equation}
\phi_{\mb{k}}=4\pi\rho_{\mb{k}}/k^{2}.
\tag{6}
\end{equation}
\phi_{\mb{k}}=4\pi\rho_{\mb{k}}/k^{2}.
\tag{6}
\end{equation}
The function \(\phi_{\mb{k}}\) is completely determined in terms of the charge density \(\rho_{\mb{k}}\); there are no dynamic differential equations to solve, involving, for example, \(\ddot{\phi}_{\mb{k}}\).
( 解答 ) 問題文で与えられている電荷密度の式 (1) を全空間で体積積分すると, ディラックの３次元の「デルタ関数」の性質
\[\int_{-\infty}^{\infty} \delta^{3}\{\mb{r}-\mb{q}(t)\}\,d^{3}\mb{r}=1\tag{7}\]
を利用して,「時刻 \(t\) に於いて, 電荷 \(e\) は位置 \(\mb{q}(t)\) に存在している」という結果を正しく与えるからである：
\begin{align*}
\int_{-\infty}^{\infty} \rho(\mb{r},t)\,d^{3}\mb{r}&=\mathrm{e}\int_{-\infty}^{\infty}\delta\{x-q_x(t)\}\,dx
\int_{-\infty}^{\infty}\delta\{y-q_y(t)\}\,dy\int_{-\infty}^{\infty}\delta\{z-q_z(t)\}\,dz\\
&=\mathrm{e}\int_{-\infty}^{\infty} \delta^{3}\{\mb{r}-\mb{q}(t)\}\,d^{3}\mb{r}=\mathrm{e} \quad\text{at}\ \,\mb{r}=\mb{q}(t)
\tag{8}
\end{align*}
次に, 式 (9-14) 中の \(\rho_k(t)\) は, 式 (9-15) とすれば良いことを示す．式 (9-15) を式 (9-14) に代入してみると,
\begin{align}
\rho(\mb{r},t)=&\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}} \tag{9-14}\\
\overset{\overset{(9-15)}{\downarrow}}{=}&\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\mathrm{e}\,e^{-i\mb{k}\cdot\mb{q}(t)}\,e^{i\mb{k}\cdot\mb{r}}
=\frac{\mathrm{e}}{(2\pi)^{3}}\int_{-\infty}^{\infty} e^{i\mb{k}\{\mb{r}-\mb{q}(t)\}}\,d^{3}\mb{k}
\tag{9}
\end{align}
\rho(\mb{r},t)=&\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}} \tag{9-14}\\
\overset{\overset{(9-15)}{\downarrow}}{=}&\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\mathrm{e}\,e^{-i\mb{k}\cdot\mb{q}(t)}\,e^{i\mb{k}\cdot\mb{r}}
=\frac{\mathrm{e}}{(2\pi)^{3}}\int_{-\infty}^{\infty} e^{i\mb{k}\{\mb{r}-\mb{q}(t)\}}\,d^{3}\mb{k}
\tag{9}
\end{align}
ここでディラックの「デルタ関数」の３次元に於ける表現式は, \(\mb{r}=(\xi,\eta,\zeta)\), \(\mb{x}=(x,y,z)\) として,
\[\delta^{3}(\mb{x}-\mb{r})=\delta(x-\xi)\,\delta(y-\eta)\,\delta(z-\zeta)=\frac{1}{(2\pi)^{3}}\int_{-\infty}^{\infty} e^{i\mb{k}\cdot(\mb{x}-\mb{r})}\,d^{3}\mb{k}\tag{10}\]
である．これを利用すると,
\begin{align}
\rho(\mb{r},t)&=\frac{\mathrm{e}}{(2\pi)^{3}}\int e^{i\mb{k}\cdot\{\mb{r}-\mb{q}(t)\}}\,d^{3}\mb{k}
=\frac{\mathrm{e}}{(2\pi)^{3}}(2\pi)^{3}\,\delta^{3}\{\mb{r}-\mb{q}(t)\}\notag\\
&=\mathrm{e}\,\delta^{3}\{\mb{r}-\mb{q}(t)\}
\tag{11}
\end{align}
\rho(\mb{r},t)&=\frac{\mathrm{e}}{(2\pi)^{3}}\int e^{i\mb{k}\cdot\{\mb{r}-\mb{q}(t)\}}\,d^{3}\mb{k}
=\frac{\mathrm{e}}{(2\pi)^{3}}(2\pi)^{3}\,\delta^{3}\{\mb{r}-\mb{q}(t)\}\notag\\
&=\mathrm{e}\,\delta^{3}\{\mb{r}-\mb{q}(t)\}
\tag{11}
\end{align}
となり, 問題文の電荷密度の式に一致した結果が得られるからである．
次に電流密度について考える．電流密度は次で定義できる：
\begin{equation}
I=\int_S \mb{j}(\mb{r})\cdot\hat{\mb{n}}dS,\quad\mathrm{where}\quad
\mb{j}(\mb{r})=\rho\,\mb{v}=\rho\,\dot{\mb{r}}
\tag{12}
\end{equation}
I=\int_S \mb{j}(\mb{r})\cdot\hat{\mb{n}}dS,\quad\mathrm{where}\quad
\mb{j}(\mb{r})=\rho\,\mb{v}=\rho\,\dot{\mb{r}}
\tag{12}
\end{equation}
図 1. 電流密度の定義
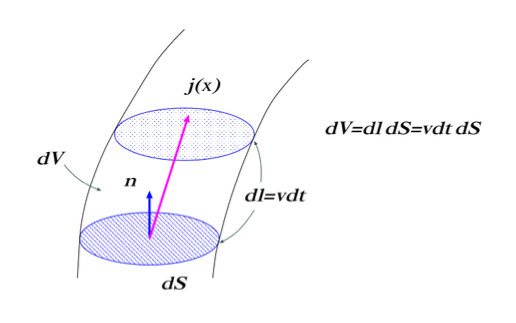
何故なら, 微小体積 \(dV=dSdl\) 中の電荷密度 \(dQ\) は, 電荷密度を \(\rho\) とすれば (上図 1. を参照),
\begin{equation}
dQ=\rho\,dV=\rho\,d\mb{l}\cdot\hat{\mb{n}}dS=\rho\,\mb{v}dt\cdot\hat{\mb{n}}dS
=\rho\,\mb{v}\cdot\hat{\mb{n}}dSdt
\tag{13}
\end{equation}
dQ=\rho\,dV=\rho\,d\mb{l}\cdot\hat{\mb{n}}dS=\rho\,\mb{v}dt\cdot\hat{\mb{n}}dS
=\rho\,\mb{v}\cdot\hat{\mb{n}}dSdt
\tag{13}
\end{equation}
従って, 微小面積 \(dS\) を通過する電流 \(dI\) は,
\begin{align}
&dI=\frac{dQ}{dt}=\rho\,\mb{v}\cdot\hat{\mb{n}}dS,\quad \mathrm{or,}\quad dI=\mb{j}\cdot\hat{\mb{n}}dS\notag\\
&\therefore\quad \rho\,\mb{v}\cdot\hat{\mb{n}}dS=\mb{j}\cdot\hat{\mb{n}}dS,\quad
\rightarrow\quad \mb{j}=\rho\,\mb{v}
\tag{14}
\end{align}
&dI=\frac{dQ}{dt}=\rho\,\mb{v}\cdot\hat{\mb{n}}dS,\quad \mathrm{or,}\quad dI=\mb{j}\cdot\hat{\mb{n}}dS\notag\\
&\therefore\quad \rho\,\mb{v}\cdot\hat{\mb{n}}dS=\mb{j}\cdot\hat{\mb{n}}dS,\quad
\rightarrow\quad \mb{j}=\rho\,\mb{v}
\tag{14}
\end{align}
従って, この電流密度の表現 \(\mb{j}=\rho\mb{v}\) に問題文の電荷密度の式と \(\mb{v}=\dot{\mb{q}}(t)\) を代入すると, 次式が得られる：
\begin{equation}
\mb{j}(\mb{r},t)=\rho\,\mb{v}=\rho(\mb{r},t)\,\dot{\mb{q}}(t)=\mathrm{e}\,\delta^{3}[\mb{r}-\mb{q}(t)]
\,\dot{\mb{q}}(t)=\mathrm{e}\,\dot{\mb{q}}(t)\,\delta^{3}[\mb{r}-\mb{q}(t)]
\tag{15}
\end{equation}
\mb{j}(\mb{r},t)=\rho\,\mb{v}=\rho(\mb{r},t)\,\dot{\mb{q}}(t)=\mathrm{e}\,\delta^{3}[\mb{r}-\mb{q}(t)]
\,\dot{\mb{q}}(t)=\mathrm{e}\,\dot{\mb{q}}(t)\,\delta^{3}[\mb{r}-\mb{q}(t)]
\tag{15}
\end{equation}
多くの電荷が存在する場合には, 式(9-14) 中に, 今度は式 (9-16) を代入して見れば良い．
まず, 電荷密度 \(\rho_{\mb{k}}\) については,
\begin{align}
\rho(\mb{r},t)&=\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\overset{\overset{(9-16)}{\downarrow}}{=}\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}} \sum_i \mathrm{e}_i\,e^{-i\mb{k}\cdot\mb{q}_i(t)}\,e^{i\mb{k}\cdot\mb{r}}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}\int_{-\infty}^{\infty} e^{i\mb{k}\cdot\{\mb{r}-\mb{q}_i(t)\}}\,d^{3}\mb{k}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}(2\pi)^{3}\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\notag\\
&=\sum_i\mathrm{e}_i\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\},\tag{16}\\
\therefore\quad \int_{-\infty}^{\infty} \rho(\mb{r},t)\,d^{3}\mb{r}&\overset{\overset{(10)}{\downarrow}}{=}
\int_{-\infty}^{\infty} \sum_i\mathrm{e}_i\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i e_i\int_{-\infty}^{\infty} \delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i e_i=Q
\tag{17}
\end{align}
\rho(\mb{r},t)&=\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\overset{\overset{(9-16)}{\downarrow}}{=}\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}} \sum_i \mathrm{e}_i\,e^{-i\mb{k}\cdot\mb{q}_i(t)}\,e^{i\mb{k}\cdot\mb{r}}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}\int_{-\infty}^{\infty} e^{i\mb{k}\cdot\{\mb{r}-\mb{q}_i(t)\}}\,d^{3}\mb{k}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}(2\pi)^{3}\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\notag\\
&=\sum_i\mathrm{e}_i\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\},\tag{16}\\
\therefore\quad \int_{-\infty}^{\infty} \rho(\mb{r},t)\,d^{3}\mb{r}&\overset{\overset{(10)}{\downarrow}}{=}
\int_{-\infty}^{\infty} \sum_i\mathrm{e}_i\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i e_i\int_{-\infty}^{\infty} \delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i e_i=Q
\tag{17}
\end{align}
電流密度 \(\mb{j}_{\mb{k}}\) についても, 同様な手順によって次となる：
\begin{align}
\mb{j}(\mb{r},t)&=\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\mb{j}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\overset{\overset{(9-16)}{\downarrow}}{=}\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_i \mathrm{e}_i\,\dot{\mb{q}}_i(t)\,e^{-i\mb{k}\cdot\mb{q}_i(t)}\,e^{i\mb{k}\cdot\mb{r}}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}\dot{\mb{q}}_i(t)\int e^{i\mb{k}\cdot(\mb{r}-\mb{q}_i(t))}\,d^{3}\mb{k}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}\dot{\mb{q}}_i(t)\,(2\pi)^{3}\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\notag\\
&=\sum_i \mathrm{e}_i\,\dot{\mb{q}}_i(t)\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\},
\tag{18}\\
\therefore\quad \int_{-\infty}^{\infty} \mb{j}(\mb{r},t)\,d^{3}\mb{r}
&\overset{\overset{(10)}{\downarrow}}{=}\int_{-\infty}^{\infty} \sum_i\mathrm{e}_i\,\dot{\mb{q}}_i(t)\,
\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i\mathrm{e}_i\,\dot{\mb{q}}_i(t)\int \delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i\mathrm{e}_i\,\dot{\mb{q}}_i(t)=\sum_i\mathrm{e}_i\,\mb{v}_i=\sum_i \mb{j}_i=I
\tag{19}
\end{align}
\mb{j}(\mb{r},t)&=\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\mb{j}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\overset{\overset{(9-16)}{\downarrow}}{=}\int_{-\infty}^{\infty} \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_i \mathrm{e}_i\,\dot{\mb{q}}_i(t)\,e^{-i\mb{k}\cdot\mb{q}_i(t)}\,e^{i\mb{k}\cdot\mb{r}}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}\dot{\mb{q}}_i(t)\int e^{i\mb{k}\cdot(\mb{r}-\mb{q}_i(t))}\,d^{3}\mb{k}\notag\\
&=\sum_i\frac{\mathrm{e}_i}{(2\pi)^{3}}\dot{\mb{q}}_i(t)\,(2\pi)^{3}\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\notag\\
&=\sum_i \mathrm{e}_i\,\dot{\mb{q}}_i(t)\,\delta^{3}\{\mb{r}-\mb{q}_i(t)\},
\tag{18}\\
\therefore\quad \int_{-\infty}^{\infty} \mb{j}(\mb{r},t)\,d^{3}\mb{r}
&\overset{\overset{(10)}{\downarrow}}{=}\int_{-\infty}^{\infty} \sum_i\mathrm{e}_i\,\dot{\mb{q}}_i(t)\,
\delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i\mathrm{e}_i\,\dot{\mb{q}}_i(t)\int \delta^{3}\{\mb{r}-\mb{q}_i(t)\}\,d^{3}\mb{r}\notag\\
&=\sum_i\mathrm{e}_i\,\dot{\mb{q}}_i(t)=\sum_i\mathrm{e}_i\,\mb{v}_i=\sum_i \mb{j}_i=I
\tag{19}
\end{align}
【 参考 】 式 (3) 以降は問題文には含まれない式とは思われるが, それらも導出しておこう．
まず, 式 (3) 及び式 (4) が言えることを示す．そのために, 次のベクトル解析の公式を利用する：
\begin{equation}
\mathrm{rot}\,(\phi\,\mb{A})=\nabla\times(\phi\,\mb{A})=\nabla\phi\times\mb{A}+\phi\,\nabla\times\mb{A}
\tag{20}
\end{equation}
\mathrm{rot}\,(\phi\,\mb{A})=\nabla\times(\phi\,\mb{A})=\nabla\phi\times\mb{A}+\phi\,\nabla\times\mb{A}
\tag{20}
\end{equation}
この公式に於いて \(\phi\to e^{i\mb{k}\cdot\mb{r}}\)， \(\mb{A}\to\mb{a}_{\mb{k}}\) とする． \(\mb{a}_{\mb{k}}\) は \(\mb{r}\) に依存しないことから \(\nabla\times\mb{a}_{\mb{k}}=0\) とすることが出来る．従って上式は次となる：
\begin{align}
\nabla\times(\mb{a}_{\mb{k}} e^{i\mb{k}\cdot\mb{r}})&=(\nabla e^{i\mb{k}\cdot\mb{r}})\times\mb{a}_{\mb{k}} +e^{i\mb{k}\cdot\mb{r}}(\nabla\times\mb{a}_{\mb{k}}) =(\nabla e^{i\mb{k}\cdot\mb{r}})\times\mb{a}_{\mb{k}}\notag\\
&=(i\mb{k}\,e^{i\mb{k}\cdot\mb{r}})\times\mb{a}_{\mb{k}}=i(\mb{k}\times\mb{a}_{\mb{k}})\,e^{i\mb{k}\cdot\mb{r}},
\tag{21}
\end{align}
\nabla\times(\mb{a}_{\mb{k}} e^{i\mb{k}\cdot\mb{r}})&=(\nabla e^{i\mb{k}\cdot\mb{r}})\times\mb{a}_{\mb{k}} +e^{i\mb{k}\cdot\mb{r}}(\nabla\times\mb{a}_{\mb{k}}) =(\nabla e^{i\mb{k}\cdot\mb{r}})\times\mb{a}_{\mb{k}}\notag\\
&=(i\mb{k}\,e^{i\mb{k}\cdot\mb{r}})\times\mb{a}_{\mb{k}}=i(\mb{k}\times\mb{a}_{\mb{k}})\,e^{i\mb{k}\cdot\mb{r}},
\tag{21}
\end{align}
式 (9-7)：\(\mb{B}=\nabla\times\mb{A}\) に式 (9-12) の \(\mb{A}\) を代入し, 上式 (21) の結果を用いると,
\begin{align}
\mb{B}&=\nabla\times\mb{A}=\nabla\times\left\{\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\mb{a}_{\mb{k}}(t)\,
e^{i\mb{k}\cdot\mb{r}} \right\}=\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\nabla\times\left\{
\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\right\}\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sqrt{4\pi}ci(\mb{k}\times\mb{a}_{\mb{k}})\,e^{i\mb{k}\cdot\mb{r}}\tag{22}
\end{align}
\mb{B}&=\nabla\times\mb{A}=\nabla\times\left\{\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\mb{a}_{\mb{k}}(t)\,
e^{i\mb{k}\cdot\mb{r}} \right\}=\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\nabla\times\left\{
\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\right\}\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sqrt{4\pi}ci(\mb{k}\times\mb{a}_{\mb{k}})\,e^{i\mb{k}\cdot\mb{r}}\tag{22}
\end{align}
この結果と, 式 (3)：\(\displaystyle{\mb{B}= \int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\mb{B}_{\mb{k}}\,e^{i\mb{k}\cdot\mb{r}}}\) を比較するならば, 式 (4) の \(\mb{B}\) の表現式が言える：
\begin{equation}
\mb{B}_{\mb{k}}=\sqrt{4\pi}ci\,(\mb{k}\times\mb{a}_{\mb{k}})
\tag{23}
\end{equation}
\mb{B}_{\mb{k}}=\sqrt{4\pi}ci\,(\mb{k}\times\mb{a}_{\mb{k}})
\tag{23}
\end{equation}
式 (9-9) から \(\displaystyle{\mb{E}=-\nabla\phi-\reverse{c}\ppdiff{\mb{A}}{t}}\) である．式 (9-14) の \(\phi,\,\mb{A}\) を用いると,
\begin{align}
\nabla\phi&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_{\mb{k}}(t)\nabla\,e^{i\mb{k}\cdot\mb{r}}
=i\mb{k}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\phi_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}},\notag\\
\pdiff{t}\mb{A}&=\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\ppdiff{\,\mb{a}_k(t)}{t}\,e^{i\mb{k}\cdot\mb{r}},
\tag{24}
\end{align}
\nabla\phi&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_{\mb{k}}(t)\nabla\,e^{i\mb{k}\cdot\mb{r}}
=i\mb{k}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\phi_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}},\notag\\
\pdiff{t}\mb{A}&=\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\ppdiff{\,\mb{a}_k(t)}{t}\,e^{i\mb{k}\cdot\mb{r}},
\tag{24}
\end{align}
従って \(\mb{E}\) は,
\begin{align}
\mb{E}&=-\nabla\phi-\reverse{c}\ppdiff{\mb{A}}{t}\notag\\
&=-i\mb{k}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\phi_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
-\reverse{c}\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\ppdiff{\,\mb{a}_{\mb{k}}(t)}{t}\,e^{i\mb{k}\cdot\mb{r}}\notag\\
\therefore\quad \mb{E}&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}\left\{-i\mb{k}\phi_{\mb{k}}(t)
-\sqrt{4\pi}\ppdiff{\,\mb{a}_{\mb{k}}(t)}{t}\right\}
\tag{25}
\end{align}
\mb{E}&=-\nabla\phi-\reverse{c}\ppdiff{\mb{A}}{t}\notag\\
&=-i\mb{k}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\phi_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
-\reverse{c}\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\ppdiff{\,\mb{a}_{\mb{k}}(t)}{t}\,e^{i\mb{k}\cdot\mb{r}}\notag\\
\therefore\quad \mb{E}&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}\left\{-i\mb{k}\phi_{\mb{k}}(t)
-\sqrt{4\pi}\ppdiff{\,\mb{a}_{\mb{k}}(t)}{t}\right\}
\tag{25}
\end{align}
この結果と式 (3)：\(\displaystyle{\mb{E}= \int\frac{d^{3}\mb{k}}{(2\pi)^{3}} \mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}}\) を比較するならば, 式 (4) の \(\mb{E}\) の表現式が言える：
\begin{equation}
\mb{E}_{\mb{k}}(t)=-i\mb{k}\,\phi_{\mb{k}}(t)-\sqrt{4\pi}\ppdiff{\,\mb{a}_{\mb{k}}(t)}{t}
=-i\mb{k}\,\phi_{\mb{k}}(t)-\sqrt{4\pi}\,\dot{\mb{a}}_{\mb{k}}(t)
\tag{26}
\end{equation}
\mb{E}_{\mb{k}}(t)=-i\mb{k}\,\phi_{\mb{k}}(t)-\sqrt{4\pi}\ppdiff{\,\mb{a}_{\mb{k}}(t)}{t}
=-i\mb{k}\,\phi_{\mb{k}}(t)-\sqrt{4\pi}\,\dot{\mb{a}}_{\mb{k}}(t)
\tag{26}
\end{equation}
また, 式 (3)：\(\displaystyle{\mb{E}= \int\frac{d^{3}\mb{k}}{(2\pi)^{3}} \mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}}\) の発散は, \(\mb{E}_{\mb{k}}\) が展開係数に過ぎないこと, 及び, 式 (26) の結果を用いて次である：
\begin{align}
\nabla\cdot\mb{E}&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\nabla\cdot\big(\mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\big)
=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\mb{E}_{\mb{k}}(t)\cdot\big(\nabla e^{i\mb{k}\cdot\mb{r}}\big)\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}i\mb{k}\cdot\mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}\,i\mb{k}\cdot
\left\{-i\mb{k}\phi_{\mb{k}}(t)-\sqrt{4\pi}\dot{\mb{a}}_{\mb{k}}(t)\right\}\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}\,\left\{-i^{2}\mb{k}^{2}\phi_{\mb{k}}(t)
-i\sqrt{4\pi}\,\mb{k}\cdot\dot{\mb{a}}_{\mb{k}}(t)\right\}
\tag{27}
\end{align}
\nabla\cdot\mb{E}&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\nabla\cdot\big(\mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\big)
=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\mb{E}_{\mb{k}}(t)\cdot\big(\nabla e^{i\mb{k}\cdot\mb{r}}\big)\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}i\mb{k}\cdot\mb{E}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}\,i\mb{k}\cdot
\left\{-i\mb{k}\phi_{\mb{k}}(t)-\sqrt{4\pi}\dot{\mb{a}}_{\mb{k}}(t)\right\}\notag\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}\,\left\{-i^{2}\mb{k}^{2}\phi_{\mb{k}}(t)
-i\sqrt{4\pi}\,\mb{k}\cdot\dot{\mb{a}}_{\mb{k}}(t)\right\}
\tag{27}
\end{align}
そして, 式 (9-14) の \(\rho\) の展開は次である：
\begin{equation}
\rho(\mb{r},t)=\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\tag{28}
\end{equation}
\rho(\mb{r},t)=\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\tag{28}
\end{equation}
以上の結果式(27) と式 (28) を, 次の式 (9-10)：
\begin{equation}
\nabla\cdot\mb{E}=4\pi\rho
\tag{9-10}
\end{equation}
\nabla\cdot\mb{E}=4\pi\rho
\tag{9-10}
\end{equation}
に代入すると,
\begin{align}
\nabla\cdot\mb{E}&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}i\mb{k}\cdot\mb{E}_{\mb{k}}(t)
\,e^{i\mb{k}\cdot\mb{r}}=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\left\{\mb{k}^{2}\phi_{\mb{k}}(t)-i\sqrt{4\pi}\,\mb{k}\cdot\dot{\mb{a}}_{\mb{k}}(t)\right\}\,e^{i\mb{k}\cdot\mb{r}}\tag{29}\\
&=4\pi\rho(\mb{r},t)
=\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,4\pi\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\tag{30}
\end{align}
\nabla\cdot\mb{E}&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}i\mb{k}\cdot\mb{E}_{\mb{k}}(t)
\,e^{i\mb{k}\cdot\mb{r}}=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\left\{\mb{k}^{2}\phi_{\mb{k}}(t)-i\sqrt{4\pi}\,\mb{k}\cdot\dot{\mb{a}}_{\mb{k}}(t)\right\}\,e^{i\mb{k}\cdot\mb{r}}\tag{29}\\
&=4\pi\rho(\mb{r},t)
=\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,4\pi\rho_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}
\tag{30}
\end{align}
この結果式 (29) と式 (30) を比較する．また, 式 (9-13) を時間微分すると \(\mb{k}\cdot\dot{\mb{a}}_k(t)=0\) である．以上から, 式 (9-17) が言える：
\begin{align}
i\mb{k}\cdot\mb{E}_{\mb{k}}(t)&=\mb{k}^{2}\phi_{\mb{k}}(t)-i\sqrt{4\pi}\,\mb{k}\cdot\dot{\mb{a}}_{\mb{k}}(t)\notag\\
&=k^{2}\phi_{\mb{k}}(t)=4\pi\rho_{\mb{k}}(t)
\tag{31}
\end{align}
i\mb{k}\cdot\mb{E}_{\mb{k}}(t)&=\mb{k}^{2}\phi_{\mb{k}}(t)-i\sqrt{4\pi}\,\mb{k}\cdot\dot{\mb{a}}_{\mb{k}}(t)\notag\\
&=k^{2}\phi_{\mb{k}}(t)=4\pi\rho_{\mb{k}}(t)
\tag{31}
\end{align}
この式 (31) すなわち式 (9-17) から,
\begin{equation}
\phi_{\mb{k}}(t)=\frac{4\pi\rho_{\mb{k}}}{k^{2}}
\tag{32}
\end{equation}
\phi_{\mb{k}}(t)=\frac{4\pi\rho_{\mb{k}}}{k^{2}}
\tag{32}
\end{equation}
となるので, 例えば \(\ddot{\phi}_{\mb{k}}\) を含むような時間を含む微分方程式を解く必要はなく, 単に電荷密度 \(\rho_{\mb{k}}(t)\) によって完全に決定されることが分かる．
