\(\)
枝松圭一著：「単一光子と量子もつれ光子(量子光学と量子光技術の基礎)」の第３章から, １次元調和振動子の波動関数に対するウィグナー関数についての記述を抜粋要約したものを示す．
１次元調和振動子の個数状態に対する座標表示 ( \(q\) 表示) の波動関数は次であった：
\def\bra#1{\langle #1 |}
\def\ket#1{| #1 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\def\BK#1#2{\langle #1 | #2 \rangle}
\psi_n(q)=\frac{1}{\pi^{1/4}\sqrt{2^{n}n!}}\,\exp\left(-\frac{q^{2}}{2}\right)H_n(q)
\tag{3.79}
\end{equation}
他方, その個数状態に対する運動量表示 ( \(p\) 表示) の波動関数は \(\phi_n(p)=\BK{p}{n}\) で定義され, 次の完全性関係と \(\BK{q}{p}\) の具体的な形,
\int_{-\infty}^{\infty} dq\,\ket{q}\bra{q}=1,\quad
\BK{q}{p}=\psi_p(q)=\frac{1}{\sqrt{2\pi}}e^{ipq}\ \rightarrow\
\BK{p}{q}=\BK{q}{p}^{*}=\frac{1}{\sqrt{2\pi}}e^{-ipq}
\end{equation*}
を用いて次式が言える：
\phi_n(p)&=\BK{p}{n}=\bra{p}\left(\int_{-\infty}^{\infty} dq\,\ket{q}\bra{q}\right)\ket{n}
=\int_{-\infty}^{\infty} dq\,\BK{p}{q}\BK{q}{n}\notag\\
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} dq\,e^{-ipq}\psi_n(q)
\tag{3.81}
\end{align}
また, そのハミルトニアン \(\displaystyle{\hat{\mathcal{H}}=\frac{\hbar\omega}{2}\Bigl(\hat{p}^{2}+\hat{q}^{2}\Bigr)}\) が \(\hat{q}\) と \(\hat{p}\) とで対称的であることから, 位相因子を除いて同じ形になる．位相因子まで含めて具体的に書き下すならば次となる：
\phi_n(p)=\BK{p}{n}=(-1)^{n}\psi_n(p)
=\frac{(-1)^{n}}{\pi^{1/4}\sqrt{2^{n}n!}}\,\exp\left(-\frac{p^{2}}{2}\right)H_n(p)
\tag{3.82}
\end{equation}
次に１次元調和振動子系が座標 \(q\) 及び運動量 \(p\) に見出される確率分布を考える．「古典的な１次元調和振動子系」では, 座標 \(q\) 及び運動量 \(p\) が一意に指定されて, \(q\) と \(p\) の張る２次元空間, すなわち「位相空間」( phase space ) 上の１点によって系の状態は定まる．しかし「その量子系」では \(q\) と \(p\) 共に「ゆらぎ ( fluctuation )」(不確定性) を持つので,「\(q\) と \(p\) は確率的にしか定まらない」．さらに, 演算子としての \(\hat{q}\) と \(\hat{p}\) は非可換であるため, その「ゆらぎ」(標準偏差) である \(\sigma(q)\) と \(\sigma(p)\) 間には「不確定性関係」 \(\sigma(q)\sigma(p)>\frac{1}{2}\) が成立する．
ウィグナー関数
量子状態である個数状態 \(\ket{n}\) にある系を座標 \(q\) に見出す「確率密度」 \(\rho(q)\), 及び運動量 \(p\) に見出す「確率密度」\(\rho(p)\) は,
\rho(q)=|\BK{q}{n}|^{2}=|\psi_{n}(q)|^{2}, \quad \rho(p)=|\BK{p}{n}|^{2}=|\phi_{n}(p)|^{2}
\end{equation*}
であり, これらは次の規格化条件を満たす：
\int_{-\infty}^{\infty} |\psi_{n}(q)|^{2}\,dq =\int_{-\infty}^{\infty} |\phi_{n}(p)|^{2}\,dp =1
\tag{3.83}
\end{equation}
では, １次元調和振動子系を「位相空間」上の点 \((q,p)\) に見出す「結合確率密度」( joint probability density ) はどうであろうか？．結合確率密度を \(w(q,p)\) とおくと, 定義により \(w(q,p)\ge 0\) であり, 次を満たすべきである：
\int_{-\infty}^{\infty}w(q,p)\,dp = |\psi_{n}(q)|^{2},\quad
\int_{-\infty}^{\infty}w(q,p)\,dq = |\phi_{n}(p)|^{2}
\tag{3.85}
\end{equation}
すなわち \(q\) や \(p\) に関する確率密度 \(|\psi_{n}(q)|^{2},|\phi_{n}(p)|^{2}\) は, 結合確率密度 \(w(q,p)\) の「周辺分布」( marginal distribution ) として与えられる．これらと式 (3.83) とから次が成り立つ：
\int_{-\infty}^{\infty}dp\int_{-\infty}^{\infty}dq\,w(q,p)=1
\tag{3.86}
\end{equation}
また, 式 (3.81) を用いると, 式 (3.85) の \(|\phi_n(p)|^{2}\) は,
\begin{align*}
|\phi_n(p)|^{2}&=\phi_n(p)\phi_n^{*}(p)\\
&=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} dq’\,e^{-ipq’}\psi_n(q’)\times \frac{1}{\sqrt{2\pi}}
\int_{-\infty}^{\infty} dq”\,e^{-ipq”}\psi_n(q”)\\
&=\frac{1}{2\pi}\int_{-\infty}^{\infty} dq’\int_{-\infty}^{\infty} dq”\,
e^{-ip(q’-q”)}\psi_n(q’)\psi_n^{*}(q”)
\end{align*}
ここで \(q’=q+\tau/2\), \(q”=q-\tau/2\) と置くと \(q’-q”=\tau\) となり,
|\phi_n(p)|^{2}&=\frac{1}{2\pi}\int_{-\infty}^{\infty} dq\int_{-\infty}^{\infty} d\tau\,
e^{-ip\tau}\psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right)
\tag{3.87}\\
&\equiv \int_{-\infty}^{\infty} dq\,W(q,p)\tag{3.90}
\end{align}
ただし最後の式の \(W(q,p)\) は次式で定義される実関数で「ウィグナー関数」( Wigner function ) と呼ばれる：
\[W(q,p)\equiv \frac{1}{2\pi}\int_{-\infty}^{\infty} d\tau\,e^{-ip\tau}\psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right),\tag{3.88}\]
\[\mathrm{or}\quad W(q,p)=\frac{1}{2\pi}\int_{-\infty}^{\infty} d\tau\,e^{-ip\tau}\Big\langle q+\frac{\tau}{2}\Big|n\Big\rangle \Big\langle n \Big| q-\frac{\tau}{2}\Big\rangle\tag{3.89}\]
式 (3.87) は, 積分の順番を入れ替えて次のように変形することも出来る：
|\phi_n(p)|^{2}&=\frac{1}{2\pi}\int_{-\infty}^{\infty} d\tau\,e^{-ip\tau}\int_{-\infty}^{\infty} dq\,
\psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right)\notag\\
&=\frac{1}{2\pi}\int_{-\infty}^{\infty} d\tau\,e^{-ip\tau}
\left\langle \psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right)\right\rangle
\tag{3.91}
\end{align}
これは, パワースペクトル \(|\phi_n(p)|^{2}\) と自己相関関数 \(\left\langle \psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right)\right\rangle\) との間のフーリエ変換の関係, すなわち「ウィーナー・ヒンチンの定理」( Wiener-Khinchine theorem ) に他ならない．つまりウィグナー関数は, ウィーナー・ヒンチンの定理に於いて自己相関関数を求める (すなわち \(q\) について積分する) 代わりに \(\tau\) についての積分を先に行ったものと見做すことが出来る．
さて, \(W(q,p)=w(q,p)\) と見做せば, 式 (3.85) が満たされることは明らかである．また,
\int_{-\infty}^{\infty}dp\,W(q,p) &=\int_{-\infty}^{\infty}dp\,\frac{1}{2\pi}\int_{-\infty}^{\infty}
d\tau\,e^{-ip\tau}\psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right)\notag\\
&=\int_{-\infty}^{\infty} d\tau\left(\frac{1}{2\pi}\int_{-\infty}^{\infty} dp\,e^{-ip\tau}\right)
\psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right)\notag\\
&=\int_{-\infty}^{\infty} d\tau\,\delta(\tau)\,
\psi_n\left(q+\frac{\tau}{2}\right)\psi_n^{*}\left(q-\frac{\tau}{2}\right)\notag\\
&=\psi_n(q)\psi_n^{*}(q)=\big|\psi_n(q)\big|^{2}
\tag{3.92}
\end{align}
となって, \(W(q,p)\) は「同時確率密度」と見做される要件を満たしている．ただし「\(W(q,p)\) は負となる場合がある」ので, \(w(q,p)\ge 0\) となるべき古典的な結合確率密度とは異なる．逆に, 量子状態では古典的結合確率密度を定義できない場合があるのである．これは, ２つの非可換な物理量の間には「不確定性関係」 \[\sigma(A)\sigma(B)\ge \frac{1}{2}\left|\left\langle [\hat{A},\hat{B}]\right\rangle\right|\] が存在し, 一般に両者を同時に決定することは出来ないことに由来する．このような理由で, \(W(q,p)\) は「擬結合確率密度」とも呼ばれる．
真空状態 \(\psi_0(q)=\pi^{-1/4}e^{-\frac{1}{2}q^{2}}\) のウィグナー関数は, 次となる：
W_0(q,p)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\tau\,e^{-ip\tau}
\psi_0\left(q+\frac{\tau}{2}\right)\psi_0^{*}\left(q-\frac{\tau}{2}\right)\notag\\
&=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\tau\,e^{-ip\tau}\frac{1}{\pi^{1/4}}
e^{-\frac{1}{2}(q+\frac{\tau}{2})^{2}}\frac{1}{\pi^{1/4}}e^{-\frac{1}{2}(q-\frac{\tau}{2})^{2}}\notag\\
&=\frac{1}{\sqrt{2}\pi}e^{-q^{2}}\cdot \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}d\tau\,e^{-ip\tau}
e^{-\frac{\tau^{2}}{4}}=\frac{1}{\sqrt{2}\pi}e^{-q^{2}}\cdot \sqrt{2}\,e^{-p^{2}}\notag\\
&=\frac{1}{\pi}e^{-q^{2}-p^{2}}
\tag{3.93}
\end{align}
従って, 個数状態 \(\ket{0}\) のウィグナー関数は「原点を中心とする等方的で正の値を持つガウス型」となる．他方, 個数状態 \(\ket{1}\) の波動関数は \(\psi_1(q)=\frac{\sqrt{2}}{\pi^{1/4}}qe^{-q^{2}/2}\) であるのでウィグナー関数は次のようになる：
W_1(q,p)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\tau\,e^{-ip\tau}
\psi_1\left(q+\frac{\tau}{2}\right)\psi_1^{*}\left(q-\frac{\tau}{2}\right)\notag\\
&=\frac{\sqrt{2}}{\pi}e^{-q^{2}}\cdot\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}d\tau\,e^{-ip\tau}\
\left(q^{2}-\frac{\tau^{2}}{4}\right)e^{-\frac{\tau^{2}}{4}}\notag\\
&=\frac{1}{\pi}\bigl(2q^{2}+2p^{2}-1\bigr)e^{-q^{2}-p^{2}}
\tag{3.93′}
\end{align}
これは原点付近で負の値となる．擬結合確率密度であるウィグナー関数が負の値を取ること (真空状態は除く) は, 非古典的な量子状態を特徴付ける性質の一つである．その意味で,「個数状態 \(\ket{n}\) とは, 非古典的な状態すなわち「量子論的な状態」なのである」．また,「個数状態に於いては, \(q\) 及び \(p\) の期待値が時間に依らず一定であった」ことからも分かるように, それらの確率密度およびウィグナー関数も時間に依らず定常である．これも古典的な調和振動子とは異なることであり,「整数値 \(n\) で特定される飛び飛びの ‘個数状態’ \(\ket{n}\) というのは, 典型的な量子論的状態である」ことを示している．
次の図は, 真空状態 \(\ket{0}\) 及び個数状態 \(\ket{1}\) に於ける「ウィグナー関数」と「確率密度 \(|\psi_n(q)|^{2}\) の時間変化」を Wolfram Cloud で作図したものである．
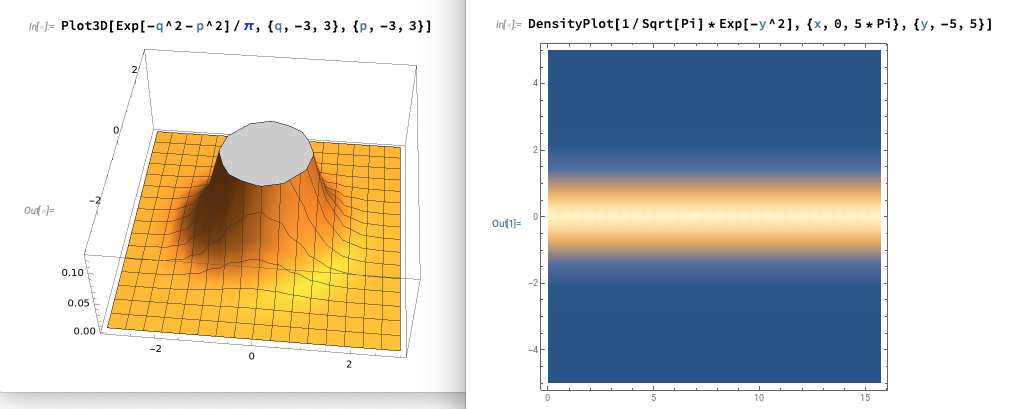
図 1. 真空状態 \(\ket{0}\) のウィグナー関数 \(W_0(q,p)\) と確率密度 \(|\psi_0(q)|^{2}=\frac{1}{\sqrt{\pi}}e^{-q^{2}}\) の時間変化(横軸は\(\omega t\)である)．
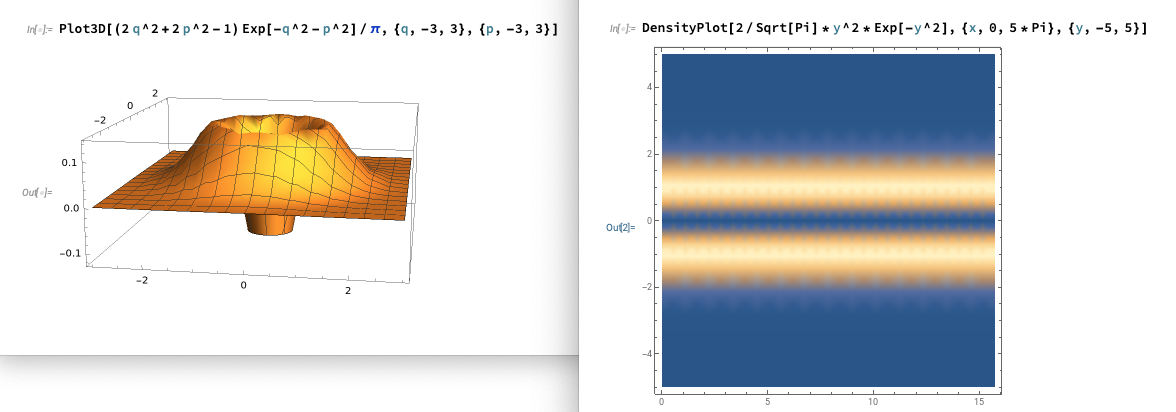
図 2. 個数状態 \(\ket{1}\) のウィグナー関数 \(W_1(q,p)\) と確率密度 \(|\psi_1(q)|^{2}=\frac{2}{\sqrt{\pi}}q^{2}e^{-q^{2}}\) の時間変化(横軸は\(\omega t\)である)．
