 ファインマン
ファインマン Feynman QED Sixteenth Lecture [Problems]
【 問題 】(1) クライン-ゴルドン方程式(スピンのない粒子)に対するラザフォード散乱公式を計算せよ.( 結果:上記の公式で \(1 - v^2 \sin^2(\theta/2)\) を \(1\) で置き換えたものになる.)(2) この...
 ファインマン
ファインマン  ファインマン
ファインマン  ファインマン
ファインマン  ファインマン
ファインマン  ファインマン
ファインマン  ファインマン
ファインマン  ファインマン
ファインマン  ファインマン
ファインマン  ファインマン
ファインマン 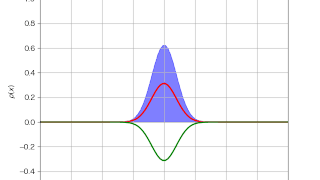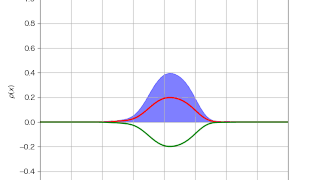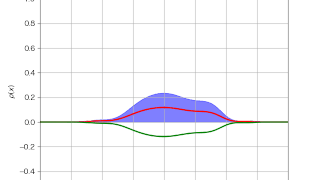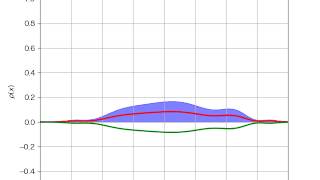 パソコン
パソコン  物理一般
物理一般  ファインマン
ファインマン