古典物理学と場中の電荷の運動方程式について


問題 6-25 の解答を書くには「場の中の電荷の運動方程式」の理解が必要と思う．その目的で「ファインマン物理Ⅱ」を読んでいたら面白い記述を見つけたので紹介しておこう．またその補足のために, 砂川：「理論電磁気学」から必要な要点を抜粋しておこう．

古典物理学のすべて

以下は「ファインマン物理学Ⅱ」の § 18-3 からの抜粋である：

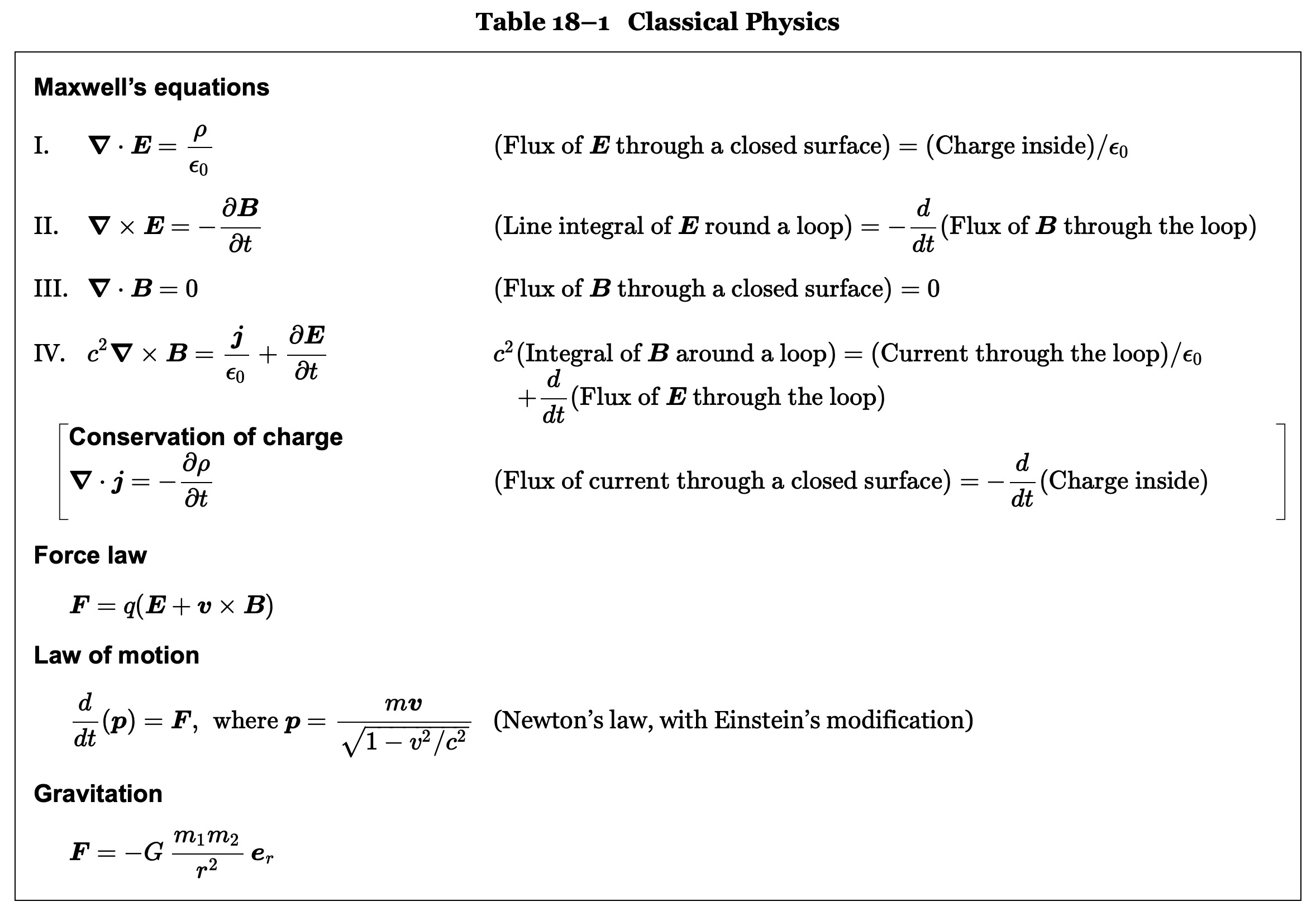
上の表 18-1 にあるのは, 基本的な古典物理学について知られている全て, すなわち, 1905年までに知れらている物理学の全てである．ここには全てが一つの表になっているのだ．これらの方程式を知れば古典物理学の全領域が理解できる．最初にあるのはマクスウェル方程式である．短い数学的形とより詳しく述べた長い形とで書いてある．次にあるのは電荷の保存則だが, それにはカッコが着いている．その理由は, マクスウェル方程式の全部が有れば, 電荷の保存則はそれらから導出できるからである．従って, 表はまだ少し冗長でさえある．次に書かれているのは「力の法則」である．電場磁場を全て知っただけでは何も分からない．何故なら, それらが電荷にどんな作用をするのかが分からなければそれらについて何も言えない．しかし $\def\mb#1{\mathbf{#1}}\mb{E}$ と $\mb{B}$ が分かると, 電荷 $q$ を持ち速度 $v$ で動く物体に及ぼす力が分かるからである．最後に, 力が分かってもそれが働くとき何が起こるかを知らねば仕方がない．つまり運動法則が要るわけで, それは「力は運動量の変化率に等しい」ということである．ここでは, 運動量を $p=m_{0}v/\sqrt{1-v^{2}/c^{2}}$ と書くことで相対論をも考慮した．完全にしたいなら, 法則をもう一つ, すなわちニュートンの重力の法則を加えるべきである．よってそれが最後に挙げてある． ~~以下略~~

ここで注目したいのは, 表中の「力の法則(Force Law)」すなわち「ローレンツ力による電荷の運動方程式」である．電磁気学の全てはマクスウェル方程式で表されていると思われがちだが, 「ローレンツ力」による電荷の運動方程式はどうも別物の公式であって, マクスウェル方程式には含まれていないらしい ^[1]次のブログ記事も参照されたい：
ローレンツ力は相対論から必然的に導出される！．このことは, 砂川もやはり第1章§7で述べている：「Maxwell 方程式を解くことにより電磁場は決定する．ここで Maxwell 方程式と共に, 荷電粒子に作用する力の法則を基本法則として挙げておこう． Maxwell 方程式とローレンツ力の式とによって表現された法則は, 電磁的現象を支配する最も基本的な自然法則であって, 電磁気学に現れてくるその他の雑多な法則は, これらの基本法則から見ると全て第２義的なものに過ぎない」． ( 例えば, オームの法則: $\mb{j}=\sigma\mb{E}$ などは, ローレンツ力による電荷の運動方程式を電媒質に当てはめることで導出される現象論的な式である).

ローレンツ力の導出

ローレンツ力を導出するには, 例えばランダウなどのように解析力学的に行うことも出来るが, ここでは砂川の第1, 2章に書かれている「電場の強さの定義式やAmpèreの力の定義式からの導出」を示しておこう．(ただし, 砂川の第12章には解析力学すなわち変分原理による導出も書かれている)．
静電場 $\mb{E}_{1}(\mb{x})$ の中に置かれた点電荷 $e$ に作用する力は $\mb{F}=e\mb{E}_{1}$ によって与えられる(これが電場の定義である)．ただし, $\mb{E}_{1}$ は外場である．もし電荷が点電荷でなく電荷密度 $\rho_{0}(\mb{x})$ で有限体積 $V$ に分布している場合には, その帯電体に作用する力は, 体積 $V$ 中の個々の電荷に働く力の和すなわち積分によって与えられる：

\begin{equation}
\mb{F}^{(e)}=\int_{V} \rho_{0}(\mb{x})\mb{E}_{1}(\mb{x})\,d^{3}\mb{x}
\tag{1}
\end{equation}

ここで注意することがある．それは外場 $\mb{E}_{1}$ の中に帯電体 $\rho_{0}$ を持ち込むと, それが作る電場 $\mb{E}_{0}$ が外場 $\mb{E}_{1}$ と重なり合って全体の電場は $\mb{E}=\mb{E}_{0}(\mb{x})+\mb{E}_{1}(\mb{x})$ となってしまうことである．よって, 帯電体に作用する力は次となるであろう：

\begin{equation}
\mb{F}^{(e)’}=\int_{V} \rho_{0}(\mb{x})\mb{E}(\mb{x})\,d^{3}\mb{x}=
\int_{V} \rho_{0}(\mb{x})\mb{E}_{0}(\mb{x})\,d^{3}\mb{x}+\int_{V} \rho_{0}(\mb{x})\mb{E}_{1}(\mb{x})\,d^{3}\mb{x}
\equiv \mb{F}_{s}^{(e)}+\mb{F}^{(e)}
\tag{2}
\end{equation}

この第1項 $\mb{F}_{s}^{(e)}$ は, 帯電体が自分自身に作用する力なので「自己力」と言い,また $\mb{E}_{0}$ は「自己場」という．しかしながら, 静電場の場合にはこの自己力はゼロであることが証明される(証明は砂川に書かれているが略す)．よって, 静電場のときは自己力の効果を考える必要はない．
全く同じことが Ampère の力, すなわち磁場 $\mb{B}(\mb{x})$ の中に定常電流 $\mb{j}(\mb{x})$ を持って来るとその $\Delta l$ の長さの部分に作用する力

\begin{equation}
\mb{F}(\mb{x})=\mb{j}(\mb{x})\times\mb{B}(\mb{x})\Delta l
\tag{3}
\end{equation}

についても成立する．つまり, 外場 $\mb{B}_{1}$ が電流密度 $\mb{j}_{0}(\mb{x})$ の定常電流に作用する力は, 定常電流 $\mb{j}_{0}(\mb{x})$ の作る自己場 $\mb{B}_{0}(\mb{x})$ も取り入れた力に一致することが示される：

\begin{equation}
\mb{F}^{(m)}=\int_{V} \mb{j}_{0}\times\mb{B}_{1}(\mb{x})\,d^{3}\mb{x}=\int_{V} \mb{j}_{0}\times\mb{B}(\mb{x})\,d^{3}\mb{x}
\tag{4}
\end{equation}

この積分中では, 長さ部分 $\Delta l$ は $d\mb{x}$ になっている訳である．また, $\mb{B}=\mb{B}_{0}(\mb{x})+\mb{B}_{1}(\mb{x})$ である．
上述のように, 電荷分布が静的であり, また電流が定常的に分布している時には自己力を考慮する必要はないが,「電荷が運動し電流が変動する時には自己力を無視することが出来ない!」ので注意が必要である．何故なら, 点電荷が自己力以外の外力の作用によって加速されるとそれは電磁波を放射し, そのために点電荷の持つ力学的エネルギーは減少してしまう．このエネルギー減少は点電荷の運動に対する減衰力を与え, それは自己力から生じるからである．よって, 自己力を考慮しないとエネルギー保存則が破られてしまうからである．
以上のことを考慮して, 微小な荷電粒子に作用する力の法則を求めよう．電荷密度が $\rho$ で電流密度が $\mb{j}$ の荷電粒子の存在する場所 $\mb{x}$ に於ける電場と磁場が $\mb{E}(\mb{x}),\,\mb{B}(\mb{x})$ であるとすると, 粒子に作用する全体の力は式 (2) と式 (4) を組み合わせた次式で与えられる：

\begin{equation}
\mb{F}=\int_{V}\big[\rho(\mb{x},t)\mb{E}(\mb{x},t)+\mb{j}(\mb{x},t)\times\mb{B}(\mb{x},t)\big]\,d^{3}\mb{x}
\tag{5}
\end{equation}

このとき, 電場も磁場も一般に自己場をも含む全電磁場であることに注意する．この式 (5) の力を「Lorentz の力」という．

電磁場中に於ける点電荷の運動方程式

古典的体系に於いて物質世界を微視的に見ると, 全ての物質は正電荷を持つ原子核と負電荷を持つ電子とに分解されてしまう．そこで電子や原子核を「点電荷」と見做し, それらの間に電磁的な相互作用が働いている体系を以ってこの世界の一つの模型と考えてもよいであろう．このとき重力は電磁的力に比較して極めて小さいので無視する．また電子や原子核は量子力学的な粒子であるから電磁場もまた量子論的に取り扱わねばならないが, ここでは全て古典的に取り扱うことにして, 粒子の運動は Newton 力学の運動法則により規程されるものとする．
最初に点電荷を数学的に表現する．点電荷とは空間のある一点に電荷 $e$ が集中したものである．従って, その電荷密度はその点で無限大になっていて, その他の全ての点でゼロである．この性質を持つ関数として Dirac の $\delta$-関数がある：

\begin{equation}
\delta(x-a)=\begin{cases} \infty & x=a,\\ 0 & x\ne a,\end{cases},
\tag{6}
\end{equation}

このとき $\delta$-関数には次の性質を持つものとする：

\begin{equation}
\delta(x)=\delta(-x),\quad \int_{-\infty}^{\infty} \delta(x-a)\,dx=1,\quad
\int_{-\infty}^{\infty} \delta(x-a)\,f(x)=f(a)
\tag{7}
\end{equation}

このような関数は本当は存在しないが, 数学的に厳密な定義は「超関数(distribution)」の理論で与えられる．
時刻 $t$ に於いて, 全電荷 $e$ を持つ点電荷の位置が $\mb{r}(t)=[x(t),y(t),z(t)]$ であるとき, その電荷密度と電流密度とはそれぞれ次で表現される：

\begin{equation}
\rho(\mb{x},t)=e\,\delta^{3}\big\{\mb{x}-\mb{r}(t)\big\},\quad
\mb{j}(\mb{x},t)=e\,\dot{\mb{r}}(t)\,\delta^{3}\big\{\mb{x}-\mb{r}(t)\big\}
\tag{8}
\end{equation}

ただし, 次のような省略記号を用いている：$$\delta^{3}\big\{\mb{x}-\mb{r}(t)\big\}\equiv\delta(x-x(t))\,\delta(y-y(t))\,\delta(z-z(t))$$
この点電荷に作用する力は, 式 (4) に上式 (8) を代入し式 (6) のデルタ関数の性質を利用することで次となる：

\begin{align}
\mb{F}(t)&=\int_{V}\big[\rho(\mb{x},t)\mb{E}(\mb{x},t)+\mb{j}(\mb{x},t)\times\mb{B}(\mb{x},t)\big]\,d^{3}\mb{x}\notag\\
&=\int \Big[ e\,\delta^{3}\big\{\mb{x}-\mb{r}(t)\big\}\mb{E}(\mb{x},t)+e\,\dot{\mb{r}}(t)\,
\delta^{3}\big\{\mb{x}-\mb{r}(t)\big\}\times\mb{B}(\mb{x},t)\Big]\,d^{3}\mb{x}\notag\\
&=e\int \mb{E}(\mb{x},t)\,\delta^{3}\big\{\mb{x}-\mb{r}(t)\big\}\,d^{3}\mb{x}
+e\int\dot{\mb{r}}(t)\times\mb{B}(\mb{x},t)\,\delta^{3}\big\{\mb{x}-\mb{r}(t)\big\}\,d^{3}\mb{x}\notag\\
&=e\mb{E}(\mb{r}(t),t) + e\,\dot{\mb{r}}(t)\times\mb{B}(\mb{r}(t),t)
\tag{9}
\end{align}

今考えている物理系が, $N$ 個の質量 $m_{i}$, 電荷 $e_{i}$ の点電荷と, それに伴う電磁場とから構成されているとするならば,「各々の点電荷はその位置 $\mb{r}_{i}(t)$ に於ける電磁場の作用の下で次のような運動方程式に従って運動する」ことになる：

\begin{equation}
m_{i}\frac{d^{2}\mb{r}_{i}(t)}{dt^{2}}=e_i\mb{E}_{i}(\mb{r}_{i}(t),t)+e_i\,\mb{v}_{i}(t)\times\mb{B}(\mb{r}_{i}(t),t),
\quad i=1,2,\dotsb N
\tag{10}
\end{equation}

ただし $\mb{v}_{i}(t)=\dot{\mb{r}}_{i}(t)$ は粒子 $i$ の速度である．

【余談】ファインマンはノーベル賞受賞の記念講演などで, 上述した「自己力」すなわち「荷電粒子が自分自身に作用する,つまり電気力はそれを作り出す粒子そのものにも作用する」という考えに言及している．ファインマンにとって「それは全く明らかと思われたこと」のようである．小生のような凡人にはすぐ理解できることではないが．しかもファインマンはMITの学部生時代に,「電子の自己エネルギーが無限大になってしまう困難さ」を説明するのに,「粒子が自分自身に作用すること, すなわち電気力はそれを作り出す粒子そのものにも作用をするという考えは必要でない」とも考えたらしい．以下はファインマン著「ご冗談でしょう, ファインマンさん」からの抜粋である：

プリンストンの大学院時代, 僕はジョン・ホィーラー教授の助手を努めた．そのときホィーラー教授にもらった研究課題が非常に難しく, やっているうちににっちもさっちも行かなくなってしまった．そこで僕はもう一度, 僕がMIT時代に持っていた一つのアイデアに立ち戻って改めて考え直すことにしたのだ．つまり電子というものは, 他の電子には働きかけるが, それ自身に働きかけることはないというのが, そのアイデアである．
これには次のような問題点が有った．電子を振動させるとエネルギーを放出し, その結果エネルギーの損失がある．ということは, そこに力が働いたということだ．さてこの力だが, 電子が電荷を帯びているときと帯びていないときとでは, これに違いがあるはずだ．(何故かと言えば, もし電荷を帯びていてもいなくてもその力が全く同じだったとすると, エネルギーの損失の在るときと無いときが出来てくる．一つの問題に答えが二つ有っては困る．)
一般の説では, 電子が自分自身に働いてこの力(放射の反作用と呼ばれている)を作るということになっているが, 僕はここでは他の電子にしか働きかけない電子を考えようというのだ．もうそのときにはすでにある困難に直面しているのに気が付いていた．(MIT時代にはその難点に気付かずにこのアイデアを思い付いたのだが, プリンストンに来た頃には, すでにこの問題があることが分かっていた．)
そこで僕はまず電子を振動させてみようと考えた．するとこの電子は近くの電子を振動させ, その結果その電子から戻って来る効果が, 放射の反作用のもとになるものと考えた訳だ．僕はこの計算をやってホィーラーに見せに行った．
するとホィーラーはすぐに「しかしちょっとおかしいんじゃないか？その力は他の電子間の距離の2乗に反比例して変化するが, 本当は決してそんな変数に左右されてはいけない訳だからね．しかも他の電子の質量に反比例的に左右されるだろうし, 他の電子の電荷に比例するんだからね」と指摘した．
これを聞いて僕は, ホィーラーがとっくに自分でもこの計算をやってしまったのだと思って意外な気がした．ホィーラーほどの学者ともなれば, 計算なんかいちいちやらなくても, 問題を一目見ればその難点がすぐにピンと来るものだということに, そのときは迂闊にも気が付かなかったのである．つまり僕みたいな駆け出しは実際に計算してみなくては分からない問題点が, 彼には計算なしでちゃんと見通せた訳だ．
彼はそう言ってからまた,「それに少し時間的にも遅れがあるだろう．波は遅れて戻って来るからね．つまり君が今説明してくれたのは結局は反射されて来る光ということになるよ．」
「ああそうか！なるほどそうですね！」
「うん．だがちょっと待った．先行する波—時間を後戻りする反応—で戻って来るとすると, 遅れずにちゃんと時間通りに戻って来ることになる．その効果は距離の2乗に反比例して変化するのは分かったとしても, 空間中に電子が一杯あったと仮定すると, その電子の数は距離の2乗に比例するから, 結局うまく補い合わせることが出来るかも知れない．」
これが可能なことは, 直に分かった．計算の結果はすっきり出たし, 引っ掛かりも無く全てがぴったり合った．この理論はマクスウェルやローレンツの標準的理論と違う処はあったかも知れないが, とにかく古典的理論として成り立ちそうだ．しかも自己作用の無限大の問題と矛盾することも無く, 作用あり遅延あり, 時間の中での前進あり後退ありというなかなか独創的な理論で, 僕たちはこれを「半先進半遅延ポテンシャル」と呼ぶことにしたのだった． ~~以下略す~~.

References[+]