散乱断面積


問題 6-9 との関連で, 小出：「量子力学 ( I )」の § 5.1 及び B. ポップら：「素粒子・原子核物理入門」の§ 4. 2 を抜粋して, 散乱理論の基本的な量である「散乱断面積」についてまとめておくことにする．

まず入射粒子も標的も古典的な弾性球である場合を考える．それらの半径を $r_1$ 及び $r_2$ とする．弾性球の間には衝突しない限り, 力は働かないとする．このとき, 両者の中心間の距離が $r_1+r_2$ より小さくなれば衝突が起こるから, 衝突が起こるかどうかだけに着目するならば, 入射粒子を大きさの無い質点と見做し, 標的粒子を半径が $a=r_1+r_2$ の球であると考えても差し支えない．すると入射粒子から見た場合, その行く先には半径 $a$ の標的が待ち構えていることになる．衝突が 1 回だけしか起こらない場合, それらの標的はまばらで, 重なり合っていることが無いときである．散乱体は, 単位体積中 $n$ 個の標的粒子を含み, 入射粒子線方向の厚さが $dx$ であるとすると, 入射粒子線に垂直な面積 $A$ の内では, 面積が $\pi a^{2}$ の標的 $n A d $ 個分が素通り不能である．従って, この物質を通り抜けるときに, 散乱を受ける粒子の全体に対する割合 $P$ は $n A d x\times \pi a^{2}$ と $A$ との比で与えられる：

\begin{equation}
P=\frac{\pi a^{2}nA\,dx}{A}=n\pi a^{2}dx
\tag{1}
\end{equation}

$\sigma=\pi a^{2}$ とおくと $\sigma$ は入射粒子から見た標的 1 個の大きさであって, 標的粒子 1 個の「断面積」(cross section) または「幾何学的反応断面積」(geometric reaction cross section) と呼ばれる．
　断面積 $\sigma$ は反応率 $\dot{N}$ すなわち「単位時間当たりの反応の合計数」で定義することも出来る．全反応率 $\dot{N}$ は入射粒子 (ビーム粒子) の単位時間当たりの数 $\dot{N}_a$ の散乱体の前と後での差に他ならない．まず, 入射ビーム束の断面積を $A$ とし粒子密度を $n_a$ とする．単位面積当たり, 単位時間当たりに標的に入射するビーム粒子数は「フラックス」(flux) $J_a$ と呼ばれ, 粒子密度 $n_a$ と粒子速度 $v_a$ との積に等しい：

\begin{equation}
J_a = \frac{\dot{N_a}}{A}=n_a \cdot v_a
\tag{2}
\end{equation}

この次元は 1/(面積)$\times$(時間) である：

\begin{equation}
\left[J_a\right]=[n_a]\cdot[v_a]=\frac{1}{L^{3}}\cdot\frac{L}{T}=\frac{1}{L^{2}\cdot T}
\end{equation}

ビームが覆う面積中に在る標的粒子の総数は $N=n\cdot A\cdot dx$ である．反応率 $\dot{N}$ は入射フラックスとビームから見た標的粒子の断面積 $\sigma_g$ の積で与えられる：

\begin{equation}
\dot{N}=J_a\cdot N\cdot \sigma_g
\tag{3}
\end{equation}

このとき, 個々の散乱中心が入射粒子に対して広げている「幾何学的反応断面積」(geometric reaction cross section) $\sigma_g$ は, 式 (3) から次のように表される：

\begin{equation}
\def\mr#1{\mathrm{#1}}
\sigma_g =\frac{\dot{N}}{J_a\cdot N} =\frac{\text{number of reaction per unit time}}{\text{beam particles per unit time per unit area}\times\mr{scattering centres}}
\tag{4}
\end{equation}

この定義は, 均一で一定なビームを仮定している (例えば, 原子炉からの中性子)．粒子加速器を用いた実験では, 次の公式が用いられる：

\begin{equation}
\sigma_g=\frac{\text{number of reaction per unit time}}{\text{beam particles per unit time}\times\text{scattering centres per unit area}}
\tag{5}
\end{equation}

なぜなら, その場合,一般にビームは空間的に均一ではないけれど, 散乱中心の面積密度は均一だからである．

　素朴に「幾何学的反応断面積」 $\sigma_g$ を標的粒子の実効的な断面積と見做すと, 多くの場合に良い近似になっている．しかし 2 粒子の反応確率は一般的に, これらの幾何学的考察による値とは大きく異なっている．更には, エネルギー依存性もまた観測される．従って, 断面積の有効的面積を決定する主なものは, 相互作用ポテンシャルの形と到達距離,及び相互作用の強さであって, 散乱過程に関係する幾何学的な形ではない．もし入射ビームの粒子フラックスと上記にように散乱中心の面積密度が分かっていれば, 反応率からその相互作用を決めることが出来る．よって,「全断面積」(total cross-section) $\sigma_{total}$ は「幾何学的反応断面積」と同様に定義される：

\begin{equation}
\sigma_{total}=\frac{\text{number of reaction per unit time}}{\text{beam particles per unit time}\times\text{scattering centres per unit area}}
\tag{6}
\end{equation}

　全断面積と同様に,「弾性」反応の断面積 $\sigma_{el}$ と「非弾性」反応の断面積 $\sigma_{inel}$ もまた定義できる．非弾性の部分は更に異なる反応チャンネルに分割することが出来る．全断面積はこれらの和である：

\begin{equation}
\sigma_{total}=\sigma_{el}+\sigma_{inel}
\tag{7}
\end{equation}

断面積は「面積」の次元を持つ物理量であり, 特定な実験の仕組みには依らない．その一般的に使用される単位は「barn」であり, それは次で定義される：

\begin{equation}
1 \mathrm{barn} = 1 \mathrm{b} = 10^{-28}\,\mathrm{m}^{2},\quad
1 \mathrm{millibarn}= 1 \mathrm{mb}= 10^{-31}\,\mathrm{m}^{2},\quad \mathrm{etc.}
\end{equation}

　衝突の仕方によって入射粒子の「散乱角」 $\theta$ は違ってくる．次の図 1. で $b$ が違うと衝突前の速度が等しくても散乱される角度が違ってくる．この $b$ を「衝突パラメータ」(impact parameter) と呼ぶ．

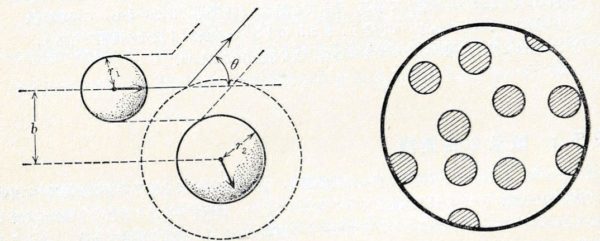
図 1. 左図中の量 $b$ を「衝突パラメータ」と呼ぶ．入射粒子から標的粒子を見た場合, 右図のように入射の方向に垂直な面積 $A$ ( 外側の大きな円 ) の中に $n A d x $ 個の標的 (斜線を引いた小さい円たちで,１つの面積は $\pi a^{2}$ である) が見える．

散乱角 $\theta$ は $b$ の関数であり, その関係は両球の質量や衝突前の速度にも関係する．$r_1+r_2$ よりも小さい $b$ で入射する全ての粒子は $\theta$ よりも大きな角度の振れを受けるであろう．そこで「$\theta$ よりも大きな振れを持つような衝突をさせるのに有効な面積」に等しい断面積を「$\theta$ 以上の角度に対する散乱の断面積」と呼び, それを $S(\theta)$ と書くならば, その $S(\theta)$ は次となる：

\begin{equation}
S(\theta)=\pi b^{2}=\pi \left(a\cos\varphi\right)^{2}=\pi a^{2}\cos^{2}\frac{\theta}{2}
\tag{8}
\end{equation}

ただし $\varphi$ は下図 2. の右図中の角度 $\varphi$ である (下の例題を参照のこと)．大きな振れを生ぜしめるように効いてくるのは散乱体の小部分でしかないことは明らかである．だから $\theta$ の増大と共に $S(\theta)$ は減少する．

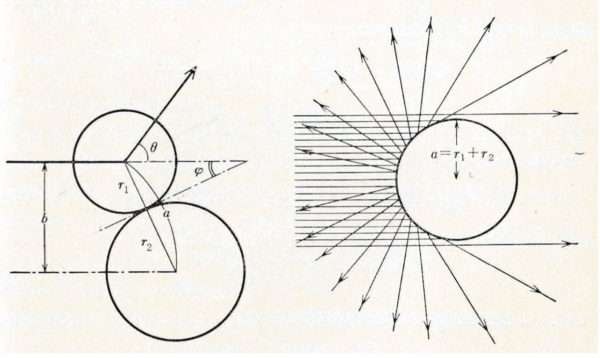
図 2. 右図から「弾性球の衝突では, 散乱されて粒子が出て来る割合は, 全ての方向で一様である」ことが分かる．

もう一つの重要な断面積は,「微分断面積」 $d\sigma(\theta)=q(\theta)d\theta$ である．これは $\theta$ と $\theta+d\theta$ の間の大きさを持った振れを生ぜしめる断面積が $\sigma(\theta)=q(\theta)d\theta$ となるように定義される．そして, これは $S(\theta)$ を $\theta$ で微分することで定義される：

\begin{equation}
q(\theta)\equiv \left|\frac{d S(\theta)}{d\theta}\right|,\quad \mr{or}\quad d\sigma(\theta)=q(\theta)\,d\theta
=\left|\frac{d S(\theta)}{d\theta}\right|\, d\theta
\tag{9}
\end{equation}

ここで絶対値が取られているのは, 上述したように $S(\theta)$ は $\theta$ の増大と共に減少するために $dS/d\theta$ の符号がマイナスになるからである．上式(9) が意味することを, 以下で見て行こう．

　$\theta=\theta(b)$ の関係が分かっていれば, 散乱角 $\theta$ に対する衝突パラメータの値 $b$ が分かることになる．そこで, 入射粒子が一つの標的 (面積 $\sigma=\pi a^{2}$) の半径 $b$ と半径 $b+db$ の円に挟まれた部分 (面積 $dS=2\pi b\,db$) に当たると, 散乱後の粒子は散乱角が $\theta$ と $\theta+d\theta$ の間で出て行く (下図 3. の左図を参照)．従って, 入射粒子が散乱角 $\theta$ と $\theta+d\theta$ の間で出て行く割合 $P’$ は式 (1) の $\sigma=\pi a^{2}$ の代わりに $dA=2\pi b\,db$ を代入した次式で与えられる：

\begin{equation}
P=n\pi a^{2}dx\quad\rightarrow\quad P’=n\,2\pi b\,db\,dx
\tag{10}
\end{equation}

上式 (10) を $b$ について $0$ から $a$ まで積分すれば式 (1) が得られることは容易に分かることである：

\begin{align}
\int_0^{a}db\,n2\pi b\,dx=n2\pi dx\int_0^{a}b\,db=2n\pi dx\left[\frac{b^{2}}{2}\right]_0^{a}=n dx\pi a^{2}
\end{align}

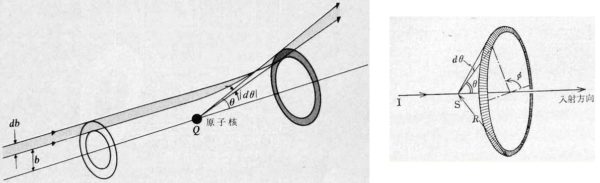
図 3.

$\theta=\theta(b)$ を逆に解いて $b=b(\theta)$ のように $b$ を $\theta$ の関数として表わし, それを $\theta$ で微分することで $db/d\theta$ を $\theta$ の関数として求め, 式 (10) を

\begin{equation}
P’=n\,dx\,2\pi b\,db=n\,dx\cdot 2\pi b\,\frac{db}{d\theta}d\theta
\tag{11}
\end{equation}

のように書いて $b$ と $db/d\theta$ に代入すれば, 入射方向となす角度が $\theta$ と $\theta+d\theta$ の間に在るような方向に散乱されて出て来る粒子の相対比率 $P’$ が $\theta$ の関数として与えられることになる．ここで

\begin{equation}
d\sigma(\theta)\equiv q(\theta)\,d\theta=2\pi b\,\frac{d b}{d\theta}d\theta
\tag{12}
\end{equation}

と書こう．この $q(\theta)$ は, 上式 (8) の $S(\theta)$ を $\theta$ で微分することによって得られる：

\begin{align}
&\frac{dS}{d\theta}=\frac{d}{d\theta}\left(\frac{d S(\theta)}{d b}\right)\frac{d b}{d\theta}
= \frac{d}{d\theta}\left(\frac{d }{d b}\pi b^{2}\right)\frac{d b}{d\theta}=2\pi b \frac{d b}{d\theta},\notag\\
&\quad \mr{therefore}\quad q(\theta) \equiv \left|\frac{dS}{d\theta}\right|=2\pi \left| b(\theta)\frac{d b}{d\theta}\right|
\tag{13}
\end{align}

この $d\sigma(\theta)=q(\theta)d\theta$ を用いると, 式 (11) は次のように書ける：

\begin{equation}
P’=n\,dx\,q(\theta)\,d\theta\equiv n\,dx\,d\sigma(\theta)
\tag{14}
\end{equation}

これは上図 3. の右図に於ける斜線を引いた部分全体を通る散乱粒子の割合であるが, すぐ分かるように $d\theta$ が同じでも $\theta$ によってこの範囲の拡がり具合は異なる．

1点を中心として見た拡がり具合の大小を表わすには, その点を中心とした単位球を切り取る面積を用いると都合が良い．これを「立体角」(solid angle) という．上図 3. の右図で $R=1$ とした場合の斜線で塗られた円輪部分の面積 $dA’$ は $2\pi\sin\theta\,d\theta$ である：

\begin{equation}
dA’=2\pi Rsin\theta\times R\,d\theta\quad\rightarrow\quad dA’=2\pi \sin \theta\,d\theta
\end{equation}

よって, 式 (11) 或いは式 (14) をこの $dA’$ で割ったものは,「入射方向との角度が $\theta$ であるような方向の単位立体角を単位時間に通過する粒子の割合」である：

\begin{equation}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
n\,dx\,d\sigma(\theta)\equiv \frac{ndx\,q(\theta)\,d\theta}{2\pi\sin\theta\,d\theta}
=\frac{\ds{n\,dx\cdot 2\pi \left| b(\theta)\frac{d b}{d\theta}\right| d\theta}}{2\pi\sin\theta\,d\theta}
=n\,dx\left|\frac{b(\theta)}{\sin\theta}\frac{db}{d\theta}\right|
\tag{15}
\end{equation}

或いは「$\theta$ 方向の微小立体角 $d\Omega$ 内に散乱されて出て行く粒子割合は,

\begin{equation}
P’=n\,dx\,d\sigma(\theta)=n\,dx\,\frac{d\sigma(\theta)}{d\Omega}\,d\Omega
\end{equation}

である」と言ってもよい．式中の $d\sigma(\theta)$ を $\theta$ 方向の「微分断面積」(differential cross section) と言う：

\begin{equation}
d\sigma(\theta)=\frac{d\sigma(\theta)}{d\Omega}d\Omega
=\left|\frac{b(\theta)}{\sin\theta}\frac{db}{d\theta}\right|
\tag{16}
\end{equation}

実験のときには, 散乱粒子を受ける検出器の開口部の大きさ (面積 $\Delta S’$ とする) は決まっているから, 散乱体からの距離を $R$ とすると, 検出器開口部の立体角は $d\Omega=\Delta S’/R^{2}$ である．よって, この検出器が受ける粒子数の割合は次で与えられることになる：

\begin{equation}
P’=n\,dx\,d\sigma(\theta)=n\,dx \frac{d\sigma(\theta)}{d\Omega} d\Omega
=n\,dx \frac{d\sigma(\theta)}{d\Omega} \cdot \frac{\Delta S’}{R^{2}}
\end{equation}

以上は標的が球対称的な場合であるが, 方向性の有る分子などがそろって並んでいるようなときには, 散乱の割合は $\theta$ だけでなく角度 $\phi$ にも関係するので $d\sigma=d\sigma(\theta,\phi)$ となる．

[ 例題 ]　標的の質量が無限大 (すなわち不動) で, 衝突が完全に滑らかな弾性衝突である場合について $q(\theta)$ と $d\sigma(\theta)$ を求めよ．

[ 解 ]　下図 4. から, 次の関係があることが分かる：

\begin{equation}
\cos \varphi =\frac{b}{a},\qquad \varphi=\frac{\theta}{2},\qquad \mr{therefore}\quad b=b(\theta)= a \cos \frac{\theta}{2}
\end{equation}

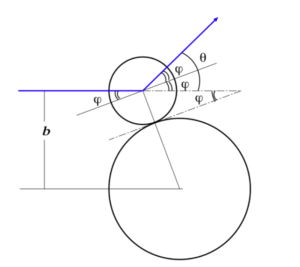
図 4.

この $b$ を $\theta$ で微分すると,

\begin{equation}
\frac{d b}{d\theta} = -\frac{a}{2}\sin \frac{\theta}{2}
\end{equation}

よって $q(\theta)=2\pi b\,db/d\theta$ は次となることが分かる：

\begin{align}
q(\theta)&= 2\pi b \frac{db}{d\theta}=2\pi \cdot a \cos\frac{\theta}{2}\cdot \left(-\frac{a}{2}\sin\frac{\theta}{2}\right)\\
&=-\pi a^{2} \sin \frac{\theta}{2}\cos\frac{\theta}{2}=-\frac{\pi}{2} a^{2}\sin\theta
\end{align}

ここで $q(\theta)$ はマイナス量であることに注意する．[式(9) とその下の記述を参照すべし]．このとき,

\begin{equation}
\sigma_{tot}=\int d\sigma(\theta)= \int_0^{\pi} q(\theta)\,d\theta = -\frac{\pi}{2} a^{2}\int_0^{\pi} \sin \theta\,d\theta =\pi a^{2}
\end{equation}

となる．これは,「全ての $\theta\, (0\sim \pi)$ についての微分断面積の合計」が「全断面積」 $\sigma_{tot}=\pi a^{2}$ に等しいという当然な結果を表している．
$d\sigma(\theta)$ は, 上式(16) から容易に求められる：

\begin{equation}
d\sigma(\theta)=\left|\frac{b(\theta)}{\sin\theta}\frac{db}{d\theta}\right|
=\left|\frac{\ds{a\cos\frac{\theta}{2}}}{\sin\theta}\cdot\left(-\frac{a}{2}\sin\frac{\theta}{2}\right) \right|
=\frac{a^{2}}{4}\frac{\ds{2\sin\frac{\theta}{2}\cos\frac{\theta}{2}}}{\sin\theta}
\end{equation}

従って, この場合の微分断面積 $d\sigma(\theta)$ は, 散乱角度 $\theta$ に依存せず一定であることが分かる：

\begin{equation}
d\sigma(\theta)=\frac{1}{4} a^{2}
\end{equation}

故に, このような弾性球の衝突では, 散乱されて粒子が出て来る割合は, 全ての方向で一様であることが分かる ( 図 2. の右図を参照すべし)．