Dirac理論に於いては, 負エネルギーの自由粒子, 例えば「負エネルギー電子」を考えることが出来るが, その負エネルギー電子の「速度」は,「運動量」の反対を向いていると考えられる．また自由電子の運動は単なる一様な直線運動ではなく,「ZitterBewegung」と呼ばれる非常に高速なジグザグ運動が付随すると考えられる．「１次元空間に於けるDirac方程式を考える」ことで, これら自由粒子の奇妙な事柄を“パソコン上でシミュレーションすることが出来る”ということが書かれた論文があったので紹介しておく．

相対論的波束の運動学の可視化(Visualizing the kinematics of relativistic wave packets)

Bernd Thaller
Institute for Mathematics and Scientific Computation,
University of Graz
Heinrichstrasse 36, A-8010 Graz, Austria
(Dated: November 26, 2024)

本稿では, 時間依存自由ディラック方程式のいくつかの解について考察する．これらの解の可視化により, 正エネルギー波と負エネルギー波の干渉によって引き起こされる奇妙な現象がすぐに明らかになる．ここで議論する効果には,「ZitterBewegung」,「負エネルギー波束に於ける運動量と速度の方向が反対であること」,「波束の局所最大値の超光速伝播(superluminal propagation of the wave packet’s local maxima)」などがある．

導入

シュレーディンガー方程式の数値シミュレーションとその解の可視化は, あらゆるレベルの量子力学教育の重要な一部となっている[1, 2, 3, 4]．しかし, ディラック方程式の数値解を試みると, 奇妙な現象につまずいてしまうことはほぼ避けられない．本稿では, これらの特異性の幾つかの可視化を示し, 非公式ではあるがその説明を試みる．

ディラック方程式は, 相対論的量子力学の基本方程式である．従って, 現代物理学で最も重要な方程式に属する．その大きな成功の中には, 水素原子のエネルギー準位の非常に正確な記述がある．一方, いくつかの未解明のパラドックスの発生は, そのステータスと解釈に疑念を投げかけている．

予想外の挙動は, 罪のないように見える初期条件でも発生する．時間依存のシュレーディンガー方程式またはディラック方程式の初期条件の正準集合は, ガウス波束の集合によって与えられる．それらは, 位置と運動量の不確定性積が最小になる様な, 多かれ少なかれ局在した量子状態を記述する．一方, ガウス型初期条件の集合は, 任意の波束を有限数のガウス型状態の重ね合わせで近似できるため, 実際的な関心のほとんどの場合をカバーする．

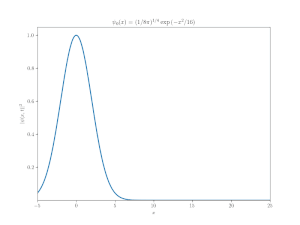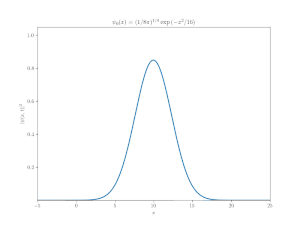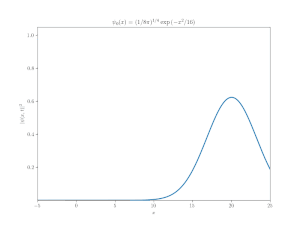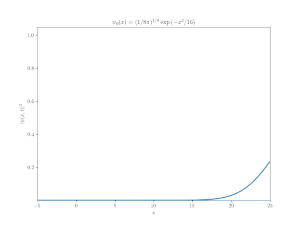
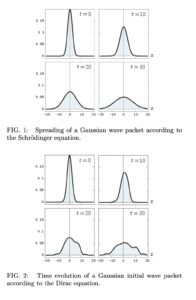
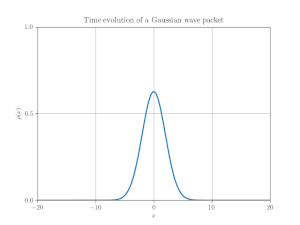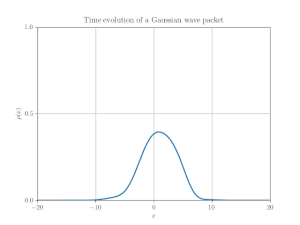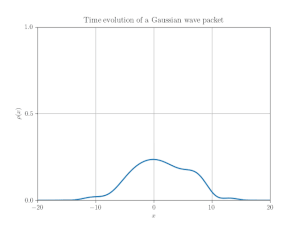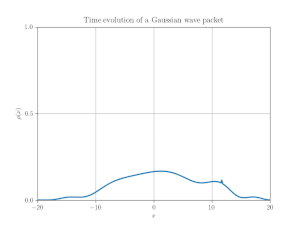
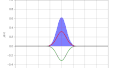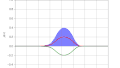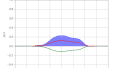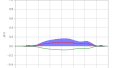
1次元自由粒子の「シュレーディンガー方程式」に従うガウス波束の運動に驚くような振る舞いはほとんどない．図 1 の例は, 平均運動量がゼロの非相対論的ガウス波束を示している．最初, 波束は十分に局在しているが, 時間とともに拡散する．波束が拡散するにつれて, 二乗可積な関数としてのそのノルムは一定でなければならないため, 波束の高さは減少する．波束は常にガウス関数である．

シュレディンガー理論によるガウス波束の時間発展

自由粒子のシュレーディンガー方程式によれば, 波束の平均位置 $⟨ x ⟩$ と平均運動量 $⟨ p ⟩$ は, 古典力学の規則に従う．さらに, 波束の拡散は波束の平均速度とは無関係である．この位置分布の拡散は, 位置空間の密度がガウス関数である古典粒子の雲でも, 粒子運動量がガウス分布している限りは観察される．

図 1. シュレーディンガー方程式によるガウス型波束の拡散．
図 2. ディラック方程式によるガウス型初期波束の時間発展．

図 2 は1次元自由粒子の「ディラック方程式」の数値解を示している．図 1 の非相対論的な波束と同じガウス型初期分布を持っているが, その挙動はまったく異なる．相対論的な波束は前後に揺れ, 時間 $t \neq 0$ では非ガウス型となり, そしてしばらくすると特徴的な「さざ波」(ripple)が起こる．

この結果は非常に奇妙なので, 量子力学に多少の経験ある(しかしディラック方程式にはない)者ならば,「この数値的解法は間違いだ」とたぶん最初は考えるであろう．これは,「方程式の数値解が現象を理解するのに十分であることはめったにない」という議論を裏付ける良い例である．この奇妙な振る舞いの起源を理解するためには, より慎重な理論的解析が必要である．

この論文には, ディラック方程式解の白黒画像がいくつか含まれている．全ての時間発展を示すコンピューター生成アニメーションは, インターネット[5]で見つけることが出来る．それらの動画は, 複素数の位相にはカラーコードを用いることで解の2成分を示している．従って, この論文の単純な白黒の位置の確率密度よりも多くの情報が明らかになる．今後の本[6]には, 同様の動画, アニメーション, シミュレーションの大規模なコレクションを収録したCD-ROMが付属するであろう．学生に「数学の公式を勉強するのでは達成するのが難しい直感的な理解」を提供するのに, それは理論的解説の説明および補足となろう．プロジェクトの背後にある詳細とアイデアについては, ウェブサイト[7]を参照してほしい．

ディラック方程式

本稿では1次元空間における自由粒子の時間依存するディラック方程式について議論する．それを, おなじみの「シュレーディンガー形式」での時間発展方程式として書く．

\begin{matrix} (1) & i ℏ \frac{d}{d t} ψ (x, t) = H_{0} ψ (x, t), ψ (x, 0) = ψ_{0} (x) \end{matrix}

自由粒子のディラックハミルトニアン

H_{0}

は行列型の微分演算子である：

H_{0} = c σ_{1} p + σ_{3} m c^{2} = (\begin{matrix} m c^{2} & - i ℏ c \frac{d}{d x} \\ - i ℏ c \frac{d}{d x} & - m c^{2} \end{matrix}), σ_{1} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}), σ_{3} = (\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix})

ここで

σ_{1}

と

σ_{3}

は有名な「パウリ行列」であり,

p = - i ℏ d / d x

である．

$H_{0}$ の式は, 相対論的なエネルギー運動量関係の線形化として解釈することが出来る：

\begin{matrix} (3) & E = λ (p) = \sqrt{c^{2} p^{2} + m^{2} c^{4}} . \end{matrix}

ディラック演算子の２乗は以下で与えられる：

\begin{matrix} (4) & H_{0}^{2} = c^{2} p^{2} + m^{2} c^{4} . \end{matrix}

数値計算と可視化の場合

ℏ = m = c = 1

の単位を使用すると有利である．これらは, 単純なスケーリング変換によって SI 単位から取得できる．従って, 以下ではディラック方程式を次の形式で使用する：

\begin{matrix} (5) & i \frac{\partial}{\partial t} ψ (x, t) = (- i σ_{1} \frac{\partial}{\partial x} + σ_{3}) ψ (x, t) . \end{matrix}

σ_{1}

と

σ_{3}

の代わりに, パウリ行列の任意のペアを使用できる．それはユニタリー的に等価な定式化になる．この記事のすべての画像は, その変換により変更されることはなくそのままである．

ここで説明する現象はより高い次元でも発生する．しかし1次元の場合は, 視覚化がはるかに簡単になる．3次元空間のディラックハミルトニアンの場合, パウリ行列は十分ではない．代わりに $4 \times 4$ – ディラック行列が必要である．本[8]には, 3次元のディラック方程式に関するより多くの情報が含まれている．

ディラックスピノルとその解釈

ディラック方程式の解に適した状態空間は, ベクトル値の関数で構成されている必要がある：

\begin{matrix} (6) & ψ (x, t) = (\begin{matrix} ψ_{1} (x, t) \\ ψ_{2} (x, t) \end{matrix}), \end{matrix}

なぜなら演算子

H_{0}

は

2 \times 2

行列だからである．これらの2成分波動関数は通常「ディラックスピノル」と呼ばれる．「スピノル」という言葉は不適切に見えるかも知れない．1次元では, スピンに影響を与える可能性のある磁場のすべては純粋なゲージ場である．従って, 式 (6) の２つの成分はスピンを記述しない．むしろ, 負のエネルギーの出現を反映している．(ただし3次元のスピノル成分の二重化はスピンによって引き起こされる.)

「運動量空間の自由ディラックハミルトニアン」は, 次の行列である：

\begin{matrix} (7) & h_{0} = (\begin{matrix} m c^{2} & c p \\ c p & - m c^{2} \end{matrix}) \end{matrix}

各

p \in R

に対して, この固有値は

λ (p)

と

- λ (p)

になる．ハミルトニアンは量子系のエネルギーを表わすので, 自由粒子エネルギーの可能な値は正または負であるという結論に至る．

それに応じて, ディラック方程式には２種類の平面波解がある．それを $u_{pos}$ と $u_{neg}$ と記すことにする．各 $p \in R$ に対して,

\begin{matrix} (8) & u_{\begin{matrix} pos \\ neg \end{matrix}} (p; x, t) = \frac{1}{\sqrt{2 π}} u_{\begin{matrix} pos \\ neg \end{matrix}} (p) e^{i p x \mp i λ (p) t}, \end{matrix}

ここで

u_{pos}

と

u_{neg}

は, 各々固有値

λ (p)

と

- λ (p)

に属する行列

h_{0} (p)

の固有ベクトルである．従って以下となる：

\begin{matrix} (9) & H_{0} u_{\begin{matrix} pos \\ neg \end{matrix}} (p; x, t) = \pm λ (p) u_{\begin{matrix} pos \\ neg \end{matrix}} (p; x, t), \end{matrix}

よって

u_{pos}

(

u_{neg}

) は「正(負)エネルギーを持つ平面波」と呼ばれる．

量子力学の形式に準拠するために, 通常は(各 $t$ に対して) ディラックスピノルの成分が二乗可積分であることを要求する：

\begin{matrix} (10) & \int_{- \infty}^{\infty} | ψ_{j} (x, t) |^{2} d x < \infty (for all t and j = 1, 2) . \end{matrix}

この数学的要件は, 解の解釈と密接に関係していることに注意すべきである．相対論的波動関数の暫定的解釈に同意するならば, 我々の選択は完全に理にかなっている．

$ψ$ が規格化されたディラックスピノルとすると, 次式は区間 $(a, b) \subset R$ 中で粒子を見出す確率である：

\begin{matrix} (11) & \int_{a}^{b} (| ψ_{1} (x, t) |^{2} + | ψ_{2} (x, t) |^{2}) d x \end{matrix}

ここで「規格化」の意味は「上記の積分を $- \infty$ から $\infty$ まで行うと $1$ に等しい」ということである．同様にして, そして非相対論的量子力学との類推で,

\begin{matrix} (12) & \int_{a}^{b} (| {\hat{ψ}}_{1} (p, t) |^{2} + | {\hat{ψ}}_{2} (p, t) |^{2}) d p \end{matrix}

は,「区間

[a, b]

に粒子の運動量が見出される確率」と解釈される．(ハットは

x

に関するフーリエ変換を表している)．この解釈は

p = - i d / d x

(空間移動の生成子) を運動量演算子として選択することと一致している．

ディラック方程式によって生成される時間発展のユニタリー性は, ディラックスピノルの規格化が時間に依存しないことを保証している．従って, 最初に1つの粒子があれば最後にも1つの粒子が存在することになる．これは任意の外場に対しても当てはまる．一般に信じられていることとは逆に, ディラック方程式は量子力学の枠組みで「対生成」は記述出来ない．それには場の量子論の形式論が必要である．そこでは多粒子波動関数が１粒子解(および負のエネルギー解に関連する１反粒子解) から構築される．

２乗可積分の波束は重ね合わせによって平面波から得られる．それはシュレーディンガー方程式と同じ方法である．適切な係数関数を用いれば, ディラック方程式の２乗可積な解は次のように書くことが出来る：

\begin{matrix} (13) & ψ (x, t) = \int_{- \infty}^{\infty} {{\hat{ψ}}_{pos} (p) u_{pos} (p; x, t) + {\hat{ψ}}_{neg} (p) u_{neg} (p; x, t)} d p \end{matrix}

係数関数

{\hat{ψ}}_{pos}

と

{\hat{ψ}}_{neg}

は, 初期状態関数

ψ (x, 0)

のフーリエ変換

\hat{ψ} (p, 0)

を正または負のエネルギー部分空間へ射影することで決定できる：

\begin{matrix} (14) & {\hat{ψ}}_{\begin{matrix} pos \\ neg \end{matrix}} (p) = P_{\begin{matrix} pos \\ neg \end{matrix}} \hat{ψ} (p, 0) = \frac{1}{2} (1 \pm \frac{h_{0} (p)}{λ (p)}) \hat{ψ} (p, 0) \end{matrix}

式 (13) の数値積分は, 任意の初期関数の自由な時間発展を計算する方法を提供し, 有限差分法の有用な代替手段となる．１次元ディラック方程式の数学については[6]を参照されたい．

本稿での考察を含む多くの理由から, 上記の解釈は批判される可能性がある．従って, この解釈は量子力学の確立された数学的形式論を適用するための便利な作業仮説に過ぎないと考えるべきである．

相対論的運動学の例

この節では, 自由ディラック方程式の解が示す3つの奇妙な現象を説明し視覚化する．いくつかの説明は以降の節で行う．

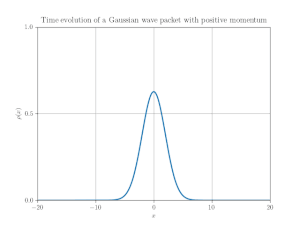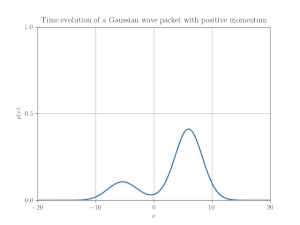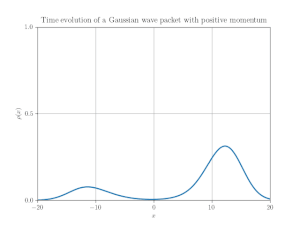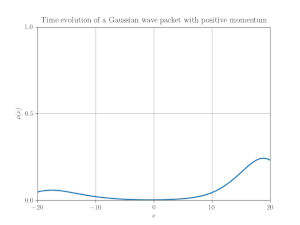
最初の例として, ガウス型ディラックスピノル

\begin{matrix} (15) & ψ (x, 0) = {(\frac{1}{32 π})}^{1 / 4} \exp (- \frac{x^{2}}{16}) (\begin{matrix} 1 \\ 1 \end{matrix}) \end{matrix}

の自由時間発展を計算してみる．図 2 に示されているのは, その計算結果のスナップショットたちである．この画像は, 上記の解釈に従った位置確率密度

| ψ_{1} (t, x) |^{2} + | ψ_{2} (t, x) |^{2}

を示している．非相対論的なガウス関数(図１)の単純な広がりと比べると, この波束は非常に複雑な動きを示している．

ガウス型ディラック-スピノルの自由時間発展

式 (15) の数値定数の選択は, 以下の考察によって動機づけられている．波束 (15) のフーリエ変換は,

\begin{matrix} (16) & \hat{ψ} (p, 0) = {(\frac{2}{π})}^{1 / 4} \exp (- 4 p^{2}) (\begin{matrix} 1 \\ 1 \end{matrix}) \end{matrix}

これは, 区間

[- 3 / 4, + 3 / 4]

によく局在した運動量分布を記述する．これは光速

c = 1

をはるかに下回る

3 / 5

以下の最大速度に相当する．従ってすべての観測は, 光速に近づく速度による相対論的影響とはほとんど関係がないと確信できる．

図 3. (図 2) の波束の平均位置値の時空ダイヤグラムと世界線．

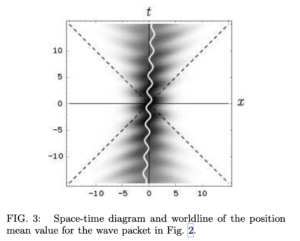
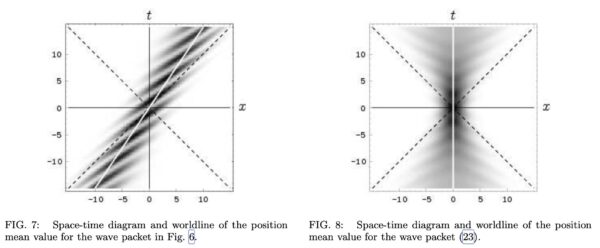
図 3 はこの解の時空ダイヤグラムである．ここで密度プロットは, 空間座標 $x$ と時間座標 $t$ の関数としての位置確率密度を無次元単位で可視化したものである．白い曲線は平均位置の世界線を示しているが, これは明らかに古典的(相対論的)運動学には従わない．その代わりに, 位置演算子の期待値は一般に「ZitterBewegung(ツィッターベべーグング)」[9]として知られる「ジグザグ運動」をしている．この急速な振動を除けば, 波束は平均運動量がゼロであるにもかかわらず, ゆっくりと右にドリフトしている．しかし (波束のフーリエ変換から求められる)運動量分布は依然として平均運動量がゼロの保存量であることが分かる．

図 4. 正の運動量を持つガウス型の初期波束の時間発展．

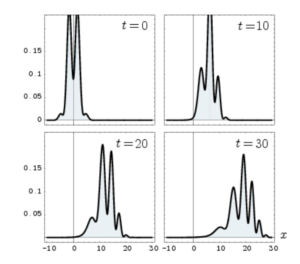
２番目の例である図 4 は, 次式の初期スピノルの自由時間発展を示している：

\begin{matrix} (17) & ψ (x, 0) = {(\frac{1}{32 π})}^{1 / 4} \exp (- \frac{x^{2}}{16} - i \frac{3 x}{4}) (\begin{matrix} 1 \\ 1 \end{matrix}) . \end{matrix}

このスピノルは式 (15) とよく似ている．位置空間では, 位相係数 $\exp (- i 3 x / 4)$ が掛け合わされている．運動量空間では, これは $3 / 4$ だけの平行移動を意味する．従って, 式 (17) に属する運動量分布は, 平均運動量 $3 / 4$ を中心とするガウス分布となる．更に, 運動量分布は非常に狭いので, 波束に大きく寄与する運動量はすべて正である．それにもかかわらず, 解は２つの部分に分裂し, 小さい方の部分は左へ(つまり負の速度で)移動している!．

正の運動量を持つ Diracスピノル波束の時間発展

図 5. (図 4) の波束の平均位置値の時空ダイヤグラムと世界線．

この解の時空図を図 5 に示すが, ここでも位置の平均値の ZitterBewegung が見られる．しかし今度は, この振動はすぐに消えてしまう．波束の左移動部分と右移動部分が位置空間である程度重なっている間だけ, ZitterBewegung が持続することが分かる．

図 6. 正の速度を持った波束の時間発展．

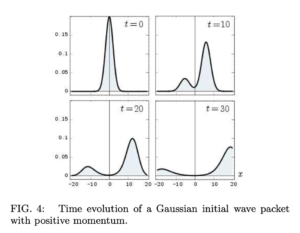
第 3 の例を図 6 に示す．これは「正の速度」を持つ波束を実現している．初期波束は, 正のエネルギー部分と負のエネルギー部分の重ね合わせとして得られる：

\begin{matrix} (18) & ψ (x, 0) = ψ_{pos} (x) + ψ_{neg} (x), \end{matrix}

正エネルギー部分は正の運動量を持つ．運動量空間に於いて, それは次で定義される：

\begin{matrix} (19) & {\hat{ψ}}_{pos} (x) = N P_{pos} \exp {- 4 {(p - \frac{4}{5})}^{2}} (\begin{matrix} 1 \\ 0 \end{matrix}) . \end{matrix}

負エネルギー部分は「負の運動量」を持ち, 次となる：

\begin{matrix} (20) & {\hat{ψ}}_{neg} (x) = N P_{neg} \exp {- 4 {(p + \frac{4}{5})}^{2}} (\begin{matrix} 0 \\ 1 \end{matrix}) . \end{matrix}

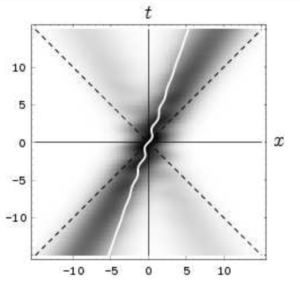
位置空間では, 両方の部分は明らかに同じ方向に運動している(速度の向きが同じ)．それらは互いに干渉し, 従って位置分布にリップルを生じている．図 7 はこの運動の時空ダイヤグラムを示している．そこに ZitterBewegung は全く存在せず, 平均位置の世界線は直線である．面白いことに, 波束のピークは超光速で移動する(干渉縞の傾きが

c

よりも寝ている)．これは奇妙なことだ．なぜなら, 少なくとも原理的には, 位置確率密度の局所的な変化は観測可能であるからだ．次は, 理論的な解析を進めよう．

図 7. (図 6) の波束の平均位置値の時空ダイヤグラムと世界線．
図 8. 波束(23)の平均位置値の時空ダイヤグラムと世界線．

パリティと運動の方向

図 2 の波束 (15) の平均速度は, 右へのゆっくりとしたドリフトを示しており, これは図 3 にはっきりと現れている．初期条件 $ψ (x, 0)$ は対称であるが, 解 $ψ (x, t)$ の方は原点での「空間反転(reflection)」に関して対称でないことは注目に値する．実際, ディラック方程式は次の置換で不変とはならない：

\begin{matrix} (21) & ψ (x, t) \to ψ (- x, t) \end{matrix}

しかし, 波動関数における

x \to - x

の置き換えは, 物理的な空間反転を記述するものではない．他のローレンツ変換と同様に, 空間反転は波動関数の成分に作用する部分を有している．ディラック方程式のヒルベルト空間における空間反転を記述する正しい方法は, 次の「パリティ変換」

\begin{matrix} (22) & P : ψ (x, t) \to σ_{3} ψ (- x, t) \end{matrix}

である．従って, 波束 (15) は「パリティ変換」の下では不変ではなく,

P ψ

は

ψ

のスカラー倍ではない．

「パリティ不変」な解の例は, ガウス型の初期波束

\begin{matrix} (23) & ψ (x, 0) = {(\frac{1}{4 π})}^{1 / 4} \exp (- \frac{x^{2}}{8}) (\begin{matrix} 1 \\ 0 \end{matrix}) \end{matrix}

によって提供される．これは上成分だけを持ち, 全時間に於いて

P ψ (x, t) = ψ (x, t)

を満足する．図 8 はこの解に対する位置確率密度の時空ダイアグラムを示している．平均の速さはゼロであり, 波束の期待値には ZitterBewegung が見られない．しかしながら, 位置の確率密度は最初の解に似たリップルを示す．

波束の平均速度は, 古典力学的な速度演算子

\begin{matrix} (24) & v_{cl} = \frac{c^{2} p}{H_{0}} \end{matrix}

によって描写される．これは, 相対論的古典力学でおなじみの運動量とエネルギーによる速度の定義に相当する．この速度と運動量の関係は, 特にエネルギーの符号に依存することに注意する．「負のエネルギーを持つ波束の場合, 正の運動量

p

は負の平均速度

v_{cl}

に対応している」．これは, 平面波 (8) の位相速度にも反映される．平面波の位相速度

v_{ph}

は次である：

\begin{matrix} (25) & v_{ph} = sign (E) \frac{λ (p)}{p} \end{matrix}

位相速度は常に光速より速く, 運動量が小さい極限では無限大になることさえあることに注意する．位相速度で情報を伝達することは出来ないので, これは問題ではない．実際, 平面波は時空間全体に拡がっており, 平面波によって伝達される全ての情報はすでに何処にでも在る．相対論的波束の群速度は常に光速より遅いか等しい．しかし, 位相速度の符号は群速度の符号に引き継がれる．

図 9. (図 6) の波束の正および負エネルギー部分の運動量分布．
図 10. (図 4) の波束の正および負エネルギー部分の運動量分布．

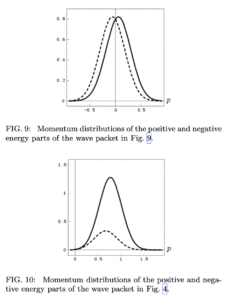
図 9 は, 図 2 の波束 (15) の正エネルギーを持つ部分と負エネルギーを持つ部分, すなわち (14) に従った関数 $| {\hat{ψ}}_{pos} (p) |^{2}$ と $| {\hat{ψ}}_{neg} (p) |^{2}$ の運動量分布を示す．正エネルギーを持つ部分は運動量分布がわずかに正の運動量にシフトしているのに対し, 負エネルギーを持つ部分は平均運動量が負になっていることが分かる．正エネルギー波束の場合, 平均運動量が正であることは, 通常通り平均速度が正であることを意味する．しかし「負エネルギー波束の場合では, 負の平均運動量は正の平均速度に対応する」．従って, 波束全体の平均速度もやはり正となり, これは図 3 を見れば一目瞭然である．「波束の負エネルギー部分に於いて速度と運動量が反対方向である」ことは, 図 4 の波束 (17) の振る舞いを即座に説明する．この波束について, 正エネルギーを持つ部分と負エネルギーを持つ部分の運動量分布を図 10 に示す．「どちらの部分も正の運動量で構成されている」ことが分かる．「負エネルギーの小さい部分は負の速度に相当する」．従って, 位置空間における波束は右へ動く正エネルギーを持ったほぼガウス型の波束と, 左へ動く負エネルギーを持つ小さい部分(平均運動量も正) の重ね合わせとなる．

図 11. (図 6) の波束の正および負エネルギー部分の運動量分布．

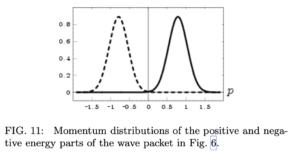
第 3 の例である図 6 の波束 (18) の場合, 図 11 に示すように負エネルギーを持つ部分は「負の運動量」( $p = - 4 / 5$ ) を持つ．ここで２つの部分は同じ大きさで,「反対の運動量を持ち, 同じ平均速度を持つ」．従って, 正エネルギーを持つ部分と負のエネルギーを持つ部分は, 位置空間で一緒に移動している．しかし２つの部分の位相方向は反対であるため, 干渉効果が生じている．平均運動量 $⟨ p ⟩$ に於いて, 初期状態は平面波 $u_{pos} (⟨ p ⟩; x, 0) + u_{neg} (- ⟨ p ⟩; x, 0)$ の重ね合わせを含んでいる．スピノルの両成分に於いて, これは $\exp (i ⟨ p ⟩ x)$ と $\exp (- i ⟨ p ⟩ x)$ の重ね合わせに比例する．正確に言うと, これは図 6 に見えるガウス型の位置確率密度に正弦関数のような歪みを引き起こす．

従って, 干渉波紋は正と負のエネルギーを持つ部分の位相干渉に起源を持つ．位相が超光速の平均速度 $v_{ph} = λ (⟨ p ⟩) / ⟨ p ⟩$ で動くように, 干渉パターンも超光速で動く．これは単なる干渉パターンであるため, 空間のある点から別の点へ情報を運ぶことはない．従って, 位置確率密度の局所的な変動は原理的に観測可能であるにもかかわらず, これらの変動が超光速で動くという事実は特殊相対性理論と矛盾しない．この効果を示す古典的な例は Moiré パターンの見かけ上の運動である．周期の長さがわずかに異なる2つの周期的パターンを互いにゆっくりとずらすと, 重ね合わせのパターン(局所的に観測可能な Moiré パターン) はほとんど任意の速度で動くことが出来る．実際, 最近議論されている超光速トンネル現象も, 平面波の干渉パターンの運動から成っている(それによって伝送される波束はその形状を変えるが, 超光速で情報が伝送されることはない)．干渉パターンの局所的な摂動は光速 $c$ 以下の速度でしか伝播できない．

ZitterBewegung の分析

ZitterBewegung (すなわち時空ダイヤグラム中の白い曲線) は, 次の演算子の (与えられた初期状態での)
期待値によって記述される：

\begin{matrix} (26) & x (t) = e^{i H_{0} t} x e^{- i H_{0} t} = x + v_{cl} (p) t + Z (t) . \end{matrix}

ここで

v_{cl}

は古典力学的な速度演算子 (24) であり, そして

Z (t)

は次の振動を記述する：

\begin{matrix} (27) & Z (t) = \frac{e^{2 i H_{0} t} - 1}{2 i H_{0}} {c σ_{1} - v_{cl} (p)} \end{matrix}

c σ_{1}

はディラック方程式に従う瞬間速度であることに注意する．なぜなら, ハイゼンベルグ描像に於ける位置の微分はちょうど次式になるからである：

\begin{matrix} (28) & \frac{d}{d t} x = i [H_{0}, x] = c σ_{1} . \end{matrix}

始状態の波束 (15) と (17) は, 演算子

σ_{1}

の固有値

+ 1

に属する固有ベクトルである．従って, これらの波束の初速度は

+ c

である．よって図 3 と図 5 に於いて, 白い曲線の

(x, t) = (0, 0)

に於ける傾きは 45° である．

運動量空間では, 関数 $Z (t)$ は $p$ の行列値関数による乗算に過ぎない．演算子 $Z (t)$ は $H_{0}$ と反交換する．これは $Z (t)$ が正エネルギーを持つ状態を負エネルギーを持つ状態に写像することを意味する．例えば $| ψ ⟩$ が正エネルギーを持つ状態であるとする．すると $Z (t) | ψ ⟩$ は負エネルギーを持ち, 従って $| ψ ⟩$ に直交する．従って, スカラー積 $⟨ ψ | Z (t) | ψ ⟩$ はゼロでなければならない．従って期待値 $⟨ ψ | Z (t) | ψ ⟩$ は, 正エネルギー部分と負エネルギー部分の両方を持つ波束に対してのみ非ゼロに成り得る．運動量空間または位置空間の異なる領域にある波束は直交する．演算子 $Z (t)$ は運動量空間に於ける乗算演算子であり, 運動量空間に於ける波束の局在特性を変えないことを意味する．従って ZitterBewegung は, 関数 ${\hat{ψ}}_{pos} (p, 0)$ が運動量空間に於ける関数 ${\hat{ψ}}_{neg} (p, 0)$ と有意な重なりを持つ場合にのみ重要となり得る．

位置空間では, 演算子 $Z (t)$ は非局所的であるが, 波束の近似的な局在をあまり変えないことが判明した．従って, 波束 $ψ (x)$ が位置空間のある領域 $R$ に(近似的に) 位置する場合, 関数 $Z (t) ψ (x)$ は近似的にその領域の近傍に位置する．その結果 ZitterBewegung が意味を持つのは, 正と負のエネルギーを持つ部分が位置空間に於いて互いに近接している場合に限られる．

では, 例題を考えてみよう．図 9 は初期波束 (15) の正エネルギー部分と負エネルギー部分の運動量分布が運動量空間で大きく重なっていることを示している．運動量(従って初期波束の運動量分布)は自由ディラック方程式に従う保存量であるため, この事実は時間が経っても変わらない．

初期波束の両部分はゼロに近い平均運動量を持ち, ゼロに近い (古典力学的)平均速度に対応する．それ故, 対応する部分は位置空間でも接近したままである．従って, この波束にとって ZitterBewegung は持続的な現象である．(実際には, ZitterBewegung の振幅は $| t | \to \infty$ のとき, 非常にゆっくりと消失する．ZitterBewegung の漸近的減衰に関する数学的議論は[8]に示されている)．

図 4 の波束の場合, 正エネルギー部分と負エネルギー部分の運動量分布は完全に重なっている(図 10 参照)．従って ZitterBewegung を観測できるが, それは２つの部分が位置空間においてほぼ同じ領域を占める場合に限られる．２つの部分は速度が正反対なのですぐに分離し, ZitterBewegung の振幅は急速に減少する．

図 6 の波束の場合, 正と負のエネルギーを持つ部分は位置空間で一緒に動くが, これらの部分は運動量空間の異なる領域に位置しているため, ZitterBewegung は起こらない．

結論

干渉効果は, 正エネルギーを持つ部分と負エネルギーを持つ部分から成るディラック方程式解に対してのみ生じる．位置分布の波紋の起源は, 正エネルギーを持つ部分と負エネルギーを持つ部分の位相方向が逆であることに在る．２乗可積分のスピノル値関数(特にガウス型スピノル) は, 一般的に正と負のエネルギーの重ね合わせであるため, ディラック方程式の数値解を計算するとこのような現象に遭遇する可能性がある．「正負のエネルギー状態の重ね合わせは物理的に観測できない」という反論もあるだろう．エネルギーの符号が一方だけの波束は ZitterBewegung を示さず, 理に適った振る舞いをする．実際, 場の量子論では１粒子ディラック方程式の正エネルギー解から多粒子電子状態のヒルベルト空間を構築し, 電荷共役負エネルギー解からは陽電子状態を構築する．この方法の問題点は,「外場の存在下では電子状態と陽電子状態を常に分離することが出来ない」ということである．

参考文献
[1] S. Brandt, H. D. Dahmen. The Picture Book of Quantum Mechanics. 2nd edition (Springer-Verlag, New York, 1995).
[2] J. M. Feagin. Quantum Methods with Mathematica, 2nd edition (Springer-Verlag, New York, 1998).
[3] M. Horbatsch. Quantum Mechanics Using Maple (Springer-Verlag, New York, 1995).
[4] B. Thaller, Visual Quantum Mechanics (Springer-Verlag, New York, 2000).
[5] https://vqm.uni-graz.at/movies.html には,この記事のスピノル波束をアニメーション化した位相カラープロットを含む QuickTime ムービーが掲載されている．
[6] B. Thaller, Advanced Visual Quantum Mechanics (Springer-Verlag, New York, 2004).
[7] https://vqm.uni-graz.at/index.html
[8] B. Thaller, The Dirac Equation, Text and Monographs in Physics (Springer-Verlag, Heidelberg, 1992).
[9] E. Schrödinger. 相対論的な量子力学における力の自由な運動について, Sitzungsber, Preuss, Akad, Wiss． Berlin,Phys.-math. Kl. $24$ (1930), 418-428.

References[+]

References
↑1	[訳註] Dirac方程式を1次元空間に於いて書くと次となる： $\begin{matrix} (2) & H = c α \cdot p + β m c^{2} \to H = c α_{1} p_{1} + β_{1} m c^{2} \end{matrix}$ このとき正方行列 $α$ と $β$ はエルミートでなければならない．それをPauli行列に採ることが出来て, 例えば $α_{1} = σ_{1}$ , $β_{1} = σ_{3}$ とすることが出来る．このとき, 式 (2) は「標準表現」と呼ぶ．

2025年4月
月	火	水	木	金	土	日
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30