 物理一般
物理一般 Feynman QED Eleventh Lecture
Eleventh Lecture\(\beta\) と \(\mathbf{\alpha}\) がエルミートであるのは, 特定の表現(in certain representations)に於いてのみであることに注意するべきである.特に, ...
 ファインマン
ファインマン 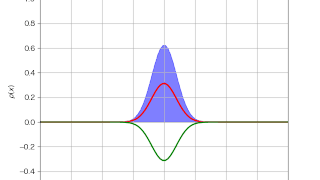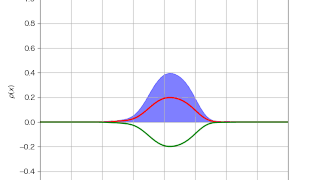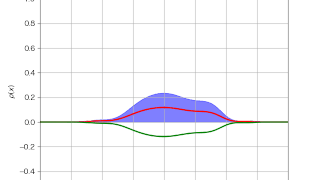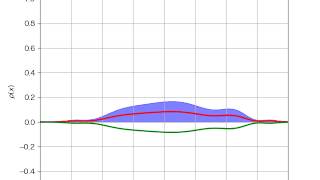 パソコン
パソコン  物理一般
物理一般  ファインマン
ファインマン  パソコン
パソコン  ファインマン
ファインマン  物理一般
物理一般  物理一般
物理一般  物理一般
物理一般  物理一般
物理一般