Feynman QED Fifteenth Lecture

量子電磁力学に於けるポテンシャル問題

量子電磁力学に於けるポテンシャル問題

Fifteenth Lecture

対生成と対消滅(PAIR CREATION AND ANNIHILATION)

状態 $ψ_{1}$ と $ψ_{2}$ 間で散乱される電子の可能な２つの経路は前講で議論した．それらは,

Case I．状態 $ψ_{1}$ と状態 $ψ_{2}$ の両方が正エネルギー状態の場合．状態 $ψ_{1}$ は「過去」の電子, 状態 $ψ_{2}$ は「未来」の電子と解釈される．これは電子の散乱である．

Case II．状態 $ψ_{1}$ と状態 $ψ_{2}$ の両方が負エネルギー状態の場合．状態 $ψ_{1}$ は「未来」の陽電子, 状態 $ψ_{2}$ は「過去」の陽電子と解釈される．これは陽電子の散乱である．

負エネルギー状態の存在は, 更に２つの型の経路を可能とする．それらは,

Case III．状態 $ψ_{1}$ は正エネルギー状態で, 状態 $ψ_{2}$ は負エネルギー状態の場合．状態 $ψ_{1}$ は「過去」の電子, 状態 $ψ_{2}$ は「過去」の陽電子と解釈される．両状態は過去にあり, 未来には何もない．これは『対消滅』(pair annihilation)を表している．

Case IV．状態 $ψ_{1}$ は負エネルギー状態で, 状態 $ψ_{2}$ は正エネルギー状態の場合．状態 $ψ_{1}$ は「未来」の陽電子, 状態 $ψ_{2}$ は「未来」の電子と解釈される．これは『対生成』(pair creation)である．

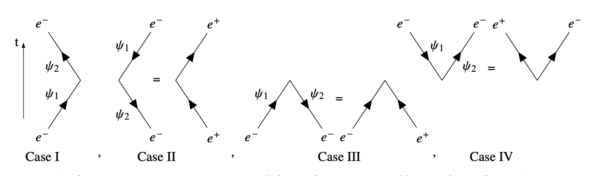
図 15-1.

４つの場合は, 上図 15-1 のように図示できる．各々のグラフに於いて, 時間は全ての場合で上向きに増加するけれども, 矢印は $ψ_{1}$ から $ψ_{2}$ へ向いていることに注意する．現時点の負エネルギー状態の解釈に於いては, 矢印は電子の運動方向を与えている．共通の言語表現では, 矢印は $p /$ が正か負かに従って, すなわち表現されている状態が「電子状態」かまたは「陽電子状態」かに従って,「正の時間方向」または「負の時間方向」を向くことになる．

エネルギーの保存(CONSERVATION OF ENERGY)

Case I の散乱に関するエネルギー関係は, 以前の講義で確立されている．Case II の時にも, 同じ結果が成り立つことは理解できる．これを示すには, Case I の時に, もし電子がエネルギー $E_{1}$ から $E_{2}$ に移行し, 摂動ポテンシャルが $\exp (- i ω t)$ に比例するように採られると, この摂動は正エネルギー $ℏ ω = ω$ をもたらすことを思い出そう．これを理解するには, 散乱振幅が次式に比例することに注意すればよい：

\begin{matrix} (15-1) & \int \exp^{*} (- i E_{2} t / ℏ) \exp (- i ω t) \exp (- i E_{1} t / ℏ) d t = \int \exp [i (E_{2} - E_{1} - ℏ ω) t / ℏ] d t \end{matrix}

すでに示されているように $E_{2}$ と $E_{1} + ω$ の間には共鳴が存在する．そのため寄与するエネルギーは $E_{2} \approx E_{1} + ω$ のものだけである．Case II の時には同じ積分が成り立つ．しかし $E_{2}$ と $E_{1}$ は負である．陽電子は(過去の)エネルギー $E_{past} = - E_{2}$ から(未来の)エネルギー $E_{fut} = - E_{1}$ へ移行する．摂動エネルギーが同じ場合, 振幅は $E_{2} = E_{1} + ω$ 即ち $- E_{past} = - E_{fut} + ω$ , 従って $E_{fut} = ω + E_{past}$ の時だけでやはり大きくなる, すなわち摂動は正のエネルギー $ω$ を持ち込む．それは電子の場合と全く同じである．

伝搬核(THE PROPAGATION KERNEL)

非相対論(シュレディンガー方程式) の場合, 波動方程式は摂動ポテンシャルを含めると次に書ける：

\begin{matrix} (15-2) & i ℏ \frac{\partial ψ}{\partial t} = H_{0} ψ + V ψ \end{matrix}

ここで

V

は摂動ポテンシャル, そして

H_{0}

は無摂動のハミルトニアンである．自由粒子の場合, 時空中の点

1

から点

2

へ粒子が移動するときの振幅を与える核(kernel) は次であることが示されている：

\begin{matrix} (15-3) & K_{0} (2, 1) = {\begin{cases} N \exp [\frac{i m (x_{2} - x_{1})^{2}}{2 ℏ (t_{2} - t_{1})}] & t_{2} > t_{1} \\ 0 & t_{2} < t_{1} \end{cases} \end{matrix}

ただし

N

は規格化因子であり, 時間間隔

t_{2} - t_{1}

と粒子の質量に依存する：

N = \sqrt{\frac{m}{2 π i ℏ (t_{2} - t_{1})}}

核は

t_{2} < t_{1}

のときはゼロと定義されるべきであることに注意する．

K_{0}

は次式を満たすことを示すことが出来る：

\begin{matrix} (15-4) & [i ℏ \frac{\partial}{\partial t_{2}} - H_{0} (2)] K_{0} (2, 1) = i ℏ δ (2, 1) \end{matrix}

摂動ポテンシャル

V

が存在する伝搬核

K_{V} (2, 1)

, それは類似した振幅を与える, は次の方程式を満たさなければならない：

\begin{matrix} (15-5) & [i ℏ \frac{\partial}{\partial t_{2}} - H_{0} (2) - V (2)] K_{V} (2, 1) = i ℏ δ (2, 1) \end{matrix}

K_{V}

は次の級数から計算することが出来ることを示すことが出来る：

\begin{aligned} K_{V} (2, 1) & = K_{0} (2, 1) - \frac{i}{ℏ} \int K_{0} (2, 3) V (3) K_{0} (3, 1) d^{3} x_{3} d t_{3} \\ (15-6) & + {(- \frac{i}{ℏ})}^{2} \int K_{0} (2, 4) V (4) K_{0} (4, 3) V (3) K_{0} (3, 1) d^{3} x_{4} d t_{4} d^{3} x_{3} d t_{3} + \dots \end{aligned}

完備な(complete) ハミルトニアン $H = H_{0} + V$ が時間に依存せず, 系の静的な状態 $ϕ_{n}$ は全て分かっている場合, 核 $K_{V} (2, 1)$ は次の和から得ることが出来る：

\begin{matrix} (15-7) & K_{V} (2, 1) = \sum_{n} \exp [- i E_{n} (t_{2} - t_{1}) / ℏ] ϕ_{n} (x_{2}) ϕ_{n}^{*} (x_{1}) \end{matrix}

これらの考えを相対論的な場合(Dirac方程式) へ拡張することは容易である．特別な形をしたハミルトニアンを選らぶと, ディラック方程式は

i ℏ \frac{\partial ψ}{\partial t} = H ψ = c α \cdot (p - \frac{e}{c} A) ψ + e ϕ ψ + m c^{2} β ψ

のように書くことが出来る．伝搬核を

K^{A} (2, 1)

と定義すると, 核は次式の解となる：

\begin{matrix} (15-8) & [i ℏ \frac{\partial}{\partial t_{2}} - e ϕ_{2} - c α \cdot (- i ℏ \nabla - \frac{e}{c} A_{2}) - m c^{2} β] K^{A} (2, 1) = i ℏ β δ (2, 1) \end{matrix}

行列

β

が最終項に挿入されているのは, ハミルトニアンから導出される核が相対論的に不変となるためである．[非相対論的な場合の式 (15-4) と類似していることに注意すべし]．この方程式に

β

を掛け合わせると, より簡潔な形となる：

\begin{matrix} (15-9) & (i ℏ \nabla /_{2} - \frac{e}{c} A /_{2} - m c) K^{A} (2, 1) = \frac{i ℏ}{c} δ (2, 1) \end{matrix}

自由粒子に対する方程式を得るには, ただ

A /_{2} = 0

とするだけである．そして, 自由粒子核を

K_{+}

と呼称するならば,

\begin{matrix} (15-10) & (i ℏ \nabla /_{2} - m c) K_{+} (2, 1) = \frac{i ℏ}{c} δ (2, 1) \end{matrix}

従って, 非相対論的な場合の自由粒子核

K_{0}

の表記を

K_{+}

で置き換え, 定義式としての式 (15-4) を式 (15-10) で置き換えたことになる．

$K_{V}$ が式 (15-6) の級数に展開できたように, やはり $K^{A}$ も次のように展開できる：

\begin{aligned} K^{A} (2, 1) & = K_{+} (2, 1) - \frac{i}{ℏ} \int K_{+} (2, 3) \frac{e}{c} A / (3) K_{+} (3, 1) d τ_{3} \\ (15-11) & + {(- \frac{i}{ℏ})}^{2} \int K_{+} (2, 3) \frac{e}{c} A / (3) K_{+} (3, 4) \frac{e}{c} A / (4) K_{+} (4, 1) d τ_{3} d τ_{4} + \dots \end{aligned}

今や「核は $4 \times 4$ 行列」であり, 従って $ψ$ の全成分は決定出来ることに注意する．この展開は真であるので, 式 (15-11) 中の項の順番は重要である．積分の要素は, 実際は４次元空間の体積要素である [cf. 式 (15-6) では $d^{3} x d t$ だったので注意する]：

d τ = d x_{0} d x_{1} d x_{2} d x_{3} = d (c t) d x

ポテンシャル

- \frac{i}{ℏ} \frac{e}{c} A / (1)

は「粒子が点

1

で一回散乱される場合の単位時間当たり単位体積当たりの振幅である」と解釈することが出来る．従って, 式 (15-11) の解釈と式 (15-6) のそれは完全に類似したものである．

【問題】式 (15-11) で定義された $K^{A}$ は, 式 (15-8) 及び式 (15-9) と両立している(consistent) ことを示せ．

〈解答例〉R.Feynman & A.Hibbs § 6-2 の式 (6-19) の導出と同様な議論から, 式 (15-11) は次式のように書き直すことが出来る：

\begin{matrix} (1) & K^{A} (2, 1) = K_{+} (2, 1) - \frac{i}{ℏ} \int d τ_{3} K_{+} (2, 3) V (3) K^{A} (3, 1), where V (3) \equiv \frac{e}{c} A / (3) \end{matrix}

すると, やはり R.Feynman & A.Hibbs § 6-2 の問題 6-3 と同様なやり方で式 (15-11) は式 (15-9) 即ち式 (15-8) を満足することを示すことが出来る．まず, 式 (1) の両辺に演算子

i ℏ \nabla /_{2}

を作用させると,

\begin{matrix} (2) & i ℏ \nabla /_{2} K^{A} (2, 1) = i ℏ \nabla /_{2} K_{+} (2, 1) - \frac{i}{ℏ} \int d τ_{3} {i ℏ \nabla /_{2} K_{+} (2, 3)} V (3) K^{A} (3, 1) \end{matrix}

このとき式 (15-10) から次式が言える：

\begin{matrix} (3) & i ℏ \nabla /_{2} K_{+} (2, 1) - m c K_{+} (2, 1) = \frac{i ℏ}{c} δ (2, 1), \to i ℏ \nabla /_{2} K_{+} (2, 3) = m c K_{+} (2, 3) + \frac{i ℏ}{c} δ (2, 3) \end{matrix}

従って,

\begin{aligned} i ℏ \nabla /_{2} & K^{A} (2, 1) = i ℏ \nabla /_{2} K_{+} (2, 1) - \frac{i}{ℏ} \int d τ_{3} {m c K_{+} (2, 3) + \frac{i ℏ}{c} δ (2, 3)} V (3) K^{A} (3, 1) \\ = i ℏ \nabla /_{2} K_{+} (2, 1) - m c \frac{i}{ℏ} \int d τ_{3} K_{+} (2, 3) V (3) K^{A} (3, 1) + \frac{1}{c} \int d τ_{3} δ (2, 3) V (3) K^{A} (3, 1) \\ (4) & = i ℏ \nabla /_{2} K_{+} (2, 1) - m c \frac{i}{ℏ} \int d τ_{3} K_{+} (2, 3) V (3) K^{A} (3, 1) + V (2) K^{A} (2, 1) \end{aligned}

ここで, 式 (1) の右辺第2項から,

\begin{matrix} (5) & - m c \frac{i}{ℏ} \int d τ_{3} K_{+} (2, 3) V (3) K^{A} (3, 1) = - m c K_{+} (2, 1) + m c K^{A} (2, 1) \end{matrix}

これを式 (4) の第2項に用い, さらに式 (15-10) を用いると,

\begin{aligned} i ℏ \nabla /_{2} K^{A} (2, 1) & = i ℏ \nabla /_{2} K_{+} (2, 1) - m c K_{+} (2, 1) + m c K^{A} (2, 1) + V (2) K^{A} (2, 1) \\ = \frac{i ℏ}{c} δ (2, 1) + m c K^{A} (2, 1) + V (2) K^{A} (2, 1) \\ ∴ i ℏ \nabla /_{2} & K^{A} (2, 1) - V (2) K^{A} (2, 1) - m c K^{A} (2, 1) = \frac{i ℏ}{c} δ (2, 1) \end{aligned}

V (2) = \frac{e}{c} A / (2)

であるから, これはまさに式 (15-9) であり, 従って式 (15-8) でもある：

\begin{matrix} (15-9) & (i ℏ \nabla /_{2} - \frac{e}{c} A / (2) - m c) K^{A} (2, 1) = \frac{i ℏ}{c} δ (2, 1) \end{matrix}

非相対論的な場合, 粒子が時間を逆に運動するような経路は排除される．しかし今回の場合, それはもはや当てはまらない．Dirac 方程式の負エネルギー固有値の存在と解釈は, そのような経路の解釈を許容し, 従ってそのような経路を含めることは許される．

$t_{4} > t_{3}$ とすることは,「仮想対」(virtual pairs) が存在することを意味する． $t_{4}$ から $t_{3}$ の区画(section) は「陽電子」(positron) の運動を表現している(図 15-2 を参照)．

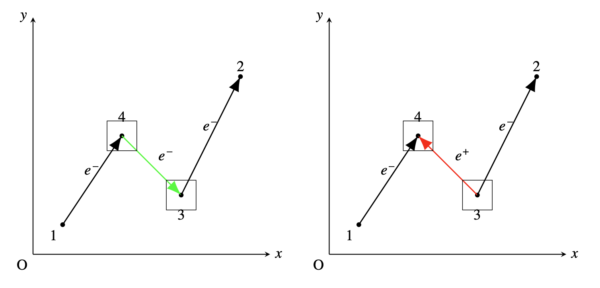
図 15-2.

時間的に定常な場の中で, もし波動関数 $ϕ_{n}$ が系の全状態について既知であるならば, その場合 $K_{+}^{A}$ は次式で定義することが出来る：

\begin{aligned} K_{+}^{A} (2, 1) & = \sum_{\begin{array}{c} pos . energies \\ t_{2} > t_{1} \end{array}} \exp [- i E_{n} (t_{2} - t_{1}) / ℏ] ϕ_{n} (x_{2}) {\tilde{ϕ}}_{n} (x_{1}) : (Case I) \\ (15-12) & = - \sum_{\begin{array}{c} neg . energies \\ t_{2} < t_{1} \end{array}} \exp [- i E_{n} (t_{2} - t_{1}) / ℏ] ϕ_{n} (x_{2}) {\tilde{ϕ}}_{n} (x_{1}) : (Case II) \end{aligned}

式 (15-9) のもう一つの解は次である：

\begin{aligned} K_{0}^{A} (2, 1) & = \sum_{pos . energies} \exp [- i E_{n} (t_{2} - t_{1}) / ℏ] ϕ_{n} (x_{2}) {\tilde{ϕ}}_{n} (x_{1}) \\ + \sum_{neg . energies} \exp [- i E_{n} (t_{2} - t_{1}) / ℏ] ϕ_{n} (x_{2}) {\tilde{ϕ}}_{n} (x_{1}), (t_{2} > t_{1}) \\ (15-13) & = 0, (t_{2} < t_{1}) \end{aligned}

式 (15-12) は「負エネルギー状態の陽電子解釈」と両立する(一致する:consistent) 解釈である．従って, 計時が「普通」 $(t_{2} > t_{1})$ ならば(the timing is “ordinary”), 存在するのは電子であり, その正エネルギー状態だけが寄与する．計時が「逆」 $(t_{2} < t_{1})$ ならば(the timing is “reversed”), 陽電子が存在し, 負エネルギー状態だけが寄与する．他方, 式 (15-13) にはそれほど納得の行く解釈を与えられない．式 (15-13) で定義される核 $K_{0}^{A}$ は式 (15-9) の数学的な解を満たすものでもあるが(それは以下で示す), 式 (15-13) は「負エネルギー状態の電子」という考えが必要となってしまう．

両方の核が共に同じ「非斉次方程式(inhomogeneous equation)」の解であることを示すために, それらの違いが全ての $t_{2}$ に対して次であることに注意する：

\sum_{neg . energies} \exp (i E_{n} t_{1} / ℏ) \exp (- i E_{n} t_{2} / ℏ) ϕ_{n} (x_{2}) {\tilde{ϕ}}_{n} (x_{1})

これは, 各々の項(term by term) が「斉次方程式(homogeneous equation)」(すなわち式(15-9)の右辺がゼロの式) の解になっている．このような２つの解が存在する可能性は「境界条件が確定していない」ことに起因する．我々は常に

K_{+}^{A}

を用いることにする．

核 $K_{+}^{A}$ は式 (15-12) で定義されるが, それはこの講義の最初で示したように Case III (対消滅) と Case IV (対生成)の取扱いを可能とする．いずれの場合も, ポテンシャル $- \frac{i}{ℏ} \frac{e}{c} A / (3)$ は陽電子の経路と電子の経路の交点で作用する．

References[+]

References
↑1	[訳註] R.Feynman & A.Hibbs § 4-1 の式 (4-29) を参照のこと．
↑2	[訳註] 演算子 $\nabla /$ の定義は次である： $\nabla / \equiv γ^{μ} \frac{\partial}{\partial x^{μ}} = γ^{0} \frac{\partial}{\partial c t} + γ \cdot \nabla = \frac{γ^{0}}{c} \frac{\partial}{\partial t} + γ \cdot \nabla, where γ^{0} = β, γ^{i} = β α_{i}$

月	火	水	木	金	土	日
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30