\(\textit{Sixth Lecture}\)
放射の平衡(Equilibrium of Radiation)
系が平衡状態にある場合, ２つの状態, 例えば \(l\) 状態と \(k\) 状態に於ける 1 立方センチメートル当りの相対原子数は, 統計力学によれば, エネルギーが \(\hbar\omega\) だけ違うとき次で与えられる：
\begin{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\mb#1{\mathbf{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\frac{N_l}{N_k}=e^{-(E_l-E_k)/kT}=e^{-\hbar\omega/kT}
\tag{1.6.1}
\end{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\mb#1{\mathbf{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\frac{N_l}{N_k}=e^{-(E_l-E_k)/kT}=e^{-\hbar\omega/kT}
\tag{1.6.1}
\end{equation}
系は平衡にあるので, 光子 \(\hbar\omega\) の吸収によって単位時間当たり状態 \(k\) から状態 \(l\) に向かう原子の数は, 放射によって \(l\) から \(k\) に向かう数と等しくなければならない．周波数 \(\omega\) の光子が １ 立方センチメートルあたり \(n_\omega\) 個存在する場合, 吸収の確率は \(n_\omega\) に比例し, 放射の確率は \(n_\omega+1\) に比例する．従って,
\begin{equation}
N_k n_\omega =N_l (n_\omega +1)
\tag{1.6.2}
\end{equation}
N_k n_\omega =N_l (n_\omega +1)
\tag{1.6.2}
\end{equation}
または,
\begin{equation}
\frac{n_\omega + 1}{n_\omega}=\frac{N_k}{N_l}=e^{\hbar\omega/kT},\quad
n_\omega = \frac{1}{e^{\hbar\omega/kT}-1}
\tag{1.6.3}
\end{equation}
\frac{n_\omega + 1}{n_\omega}=\frac{N_k}{N_l}=e^{\hbar\omega/kT},\quad
n_\omega = \frac{1}{e^{\hbar\omega/kT}-1}
\tag{1.6.3}
\end{equation}
これはプランクの黒体放射分布則である．
光の散乱(The Scattering of Light)
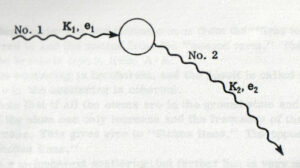
ここでは, 入射した光子が原子によって新しい方向に(そしてたぶん新しいエネルギーで) 散乱される事象について述べる(図1.6 参照)．これは原子による入射光子の吸収と新しい光子の放射と考えることが出来る．この事象に関与する 2 つの光子はベクトルポテンシャルで表わされる．第3講で \(\mb{A}=a\mb{e}\exp\{-i(\omega t -\mb{K}\cdot\mb{x})\}\) そして \(a=\sqrt{2\pi \hbar c^{2}/\omega}\) であった．そこで入射光子を\(\mb{A}_1\)とし, 放射光子を\(\mb{A}_2\)として次とする：
\begin{equation}
\mb{A}_1 =\mb{A}_1^{\mathrm{(abs)}} = c\sqrt{\frac{2\pi\hbar}{\omega_1}}\,\mb{e}_1\,e^{-i(\omega_1 t-\mb{K}\cdot\mb{x})},\qquad
\mb{A}_2 =\mb{A}_2^{\mathrm{(emis)}} = c\sqrt{\frac{2\pi\hbar}{\omega_2}}\,\mb{e}_2\,e^{+i(\omega_2 t-\mb{K}\cdot\mb{x})}
\tag{1.6.4}
\end{equation}
\mb{A}_1 =\mb{A}_1^{\mathrm{(abs)}} = c\sqrt{\frac{2\pi\hbar}{\omega_1}}\,\mb{e}_1\,e^{-i(\omega_1 t-\mb{K}\cdot\mb{x})},\qquad
\mb{A}_2 =\mb{A}_2^{\mathrm{(emis)}} = c\sqrt{\frac{2\pi\hbar}{\omega_2}}\,\mb{e}_2\,e^{+i(\omega_2 t-\mb{K}\cdot\mb{x})}
\tag{1.6.4}
\end{equation}
決定すべき数値は, 最初に状態 \(k\) にある原子が時間 \(T\) の間に摂動 \(\mb{A} = \mb{A}_1 + \mb{A}_2\) の作用によって状態 \(l\) のままとなる確率である．この確率は, 他の遷移確率と同様に \(A_{lk}\) を用いて計算することが出来る [1]ファインマン経路積分の § 6-5 より, 遷移振幅 \(\lambda_{mn}\) は次の式 (6-69), 式 (6-72), 式 (6-74) … Continue reading．
図 6-1
ただし遷移振幅 \(A_{lk}\) は,
\begin{align}
A_{lk}&=\delta_{lk}\,\exp\Bigl\{-i\frac{E_l }{\hbar}T\Bigr\}-\frac{i}{\hbar}\int_{0}^{T}dt_3\,
\exp\Bigl\{-i\frac{E_l}{\hbar}(T-t_3)\Bigr\} U_{lk}(t_3)\exp\Bigl\{-i\frac{E_k}{\hbar}t_3\Bigr\}\notag\\
&+\left(-\frac{i}{\hbar}\right)^{2}\sum_n \int_{0}^{T}dt_4\int_{0}^{t_4}dt_3\,
\exp\Bigl\{-i\frac{E_l}{\hbar}(T-t_4)\Bigr\} U_{ln}(t_4)\exp\Bigl\{-i\frac{E_n}{\hbar}(t_4-t_3)\Bigr\}
U_{nk}(t_3)\exp\Bigl\{-i\frac{E_k}{\hbar}t_3\Bigr\}
\tag{1.6.5}
\end{align}
A_{lk}&=\delta_{lk}\,\exp\Bigl\{-i\frac{E_l }{\hbar}T\Bigr\}-\frac{i}{\hbar}\int_{0}^{T}dt_3\,
\exp\Bigl\{-i\frac{E_l}{\hbar}(T-t_3)\Bigr\} U_{lk}(t_3)\exp\Bigl\{-i\frac{E_k}{\hbar}t_3\Bigr\}\notag\\
&+\left(-\frac{i}{\hbar}\right)^{2}\sum_n \int_{0}^{T}dt_4\int_{0}^{t_4}dt_3\,
\exp\Bigl\{-i\frac{E_l}{\hbar}(T-t_4)\Bigr\} U_{ln}(t_4)\exp\Bigl\{-i\frac{E_n}{\hbar}(t_4-t_3)\Bigr\}
U_{nk}(t_3)\exp\Bigl\{-i\frac{E_k}{\hbar}t_3\Bigr\}
\tag{1.6.5}
\end{align}
または,
\begin{align*}
A_{lk}&=e^{-iE_l T/\hbar}\{c_k(0)+c_l^{(1)}(T)+c_l^{(2)}(T)\},\tag{1.6.5′}\\
&c_k(0)=\delta_{lk},\\
&c_l^{(1)}(T)=-\frac{i}{\hbar}\int_{0}^{T}dt_3\,U_{lk}(t_3)\,e^{i(E_l-E_k)t_3/\hbar},\\
&c_l^{(2)}(T)=\left(-\frac{i}{\hbar}\right)^{2}\sum_n \int_{0}^{T}dt_4\int_{0}^{t_4}\,U_{ln}(t_4)\,
e^{i(E_l-E_n)t_4/\hbar}\,U_{nk}(t_3)\,e^{i(E_n-E_k)t_3/\hbar}
\end{align*}
双極子近似が採用され, そして
\begin{equation}
\Delta H =e^{i\omega t}U = -\frac{e}{mc}\mb{A}\cdot\mb{p}+\frac{e^{2}}{2mc^{2}}\mb{A}\cdot\mb{A}
\tag{1.6.6}
\end{equation}
\Delta H =e^{i\omega t}U = -\frac{e}{mc}\mb{A}\cdot\mb{p}+\frac{e^{2}}{2mc^{2}}\mb{A}\cdot\mb{A}
\tag{1.6.6}
\end{equation}
ただしスピンは無視している [2]スピンを無視するので, 第3講の式 (3.11) の第 3 項は含めない．そのときの摂動 \(U\)は 次となる： \begin{equation*} \Delta H … Continue reading．
\(A_{lk}\) を定義する各積分に於いて, ２つのベクトルポテンシャルの各々が出現するのは一度だけでなければならない．従って, 最初の積分では \(U\) の項 \(\mb{p}\cdot\mb{A}\) は \(U_{lk}\) には現れない．そして積 \(\mb{A}\cdot\mb{A}=(\mb{A}_1+\mb{A}_2)\cdot(\mb{A}_1+\mb{A}_2)\) はその交差項 \(2\mb{A}_1\cdot\mb{A}_2\) のみが寄与する[3]入射光子の吸収と光子の放射が起こらねばならないので, 遷移振幅を表す項には入射光子を表わす \(\mb{A}_1\) と放射光子を表わす \(\mb{A}_2\) が 1 … Continue reading．
2番目の積分は \(\mb{A}\cdot\mb{A}\) からの寄与は無く, そして 2 項の和となる．第 1 項は \(\mb{A}_2\cdot\mb{p}\) に基づく \(U_{ln}\) と \(\mb{A}_1\cdot\mb{p}\) に基づく \(U_{nk}\) を含んでいる．第 2 項は \(\mb{A}_1\cdot\mb{p}\) に基づく \(U_{ln}\) と \(\mb{A}_2\cdot\mb{p}\) に基づく \(U_{nk}\) を持つ．時間系列はこれらの 2 項に帰着するが, それは模式的に図 6-2 のように表すことが出来る．
図 6-2
さて次は, 第 1 項から得られる積分について詳しく説明しよう．
\begin{equation}
(\mb{A}_1\cdot\mb{p})_{nk}=c\sqrt{\frac{2\pi\hbar}{\omega_1}}\,(\mb{p}\cdot\mb{e}_1)_{nk}\,e^{-i\omega_1 t},\qquad
(\mb{A}_2\cdot\mb{p})_{ln}=c\sqrt{\frac{2\pi\hbar}{\omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}\,e^{i\omega_2 t}
\tag{1.6.7}
\end{equation}
(\mb{A}_1\cdot\mb{p})_{nk}=c\sqrt{\frac{2\pi\hbar}{\omega_1}}\,(\mb{p}\cdot\mb{e}_1)_{nk}\,e^{-i\omega_1 t},\qquad
(\mb{A}_2\cdot\mb{p})_{ln}=c\sqrt{\frac{2\pi\hbar}{\omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}\,e^{i\omega_2 t}
\tag{1.6.7}
\end{equation}
その結果, 積分は
\begin{align*}
&\left(-\frac{i}{\hbar}\right)^{2}\sum_n \int_{0}^{T}dt_4\int_{0}^{t_4}dt_3\,
\exp\Bigl\{-i\frac{E_l}{\hbar}(T-t_4)\Bigr\} U_{ln}(t_4)\exp\Bigl\{-i\frac{E_n}{\hbar}(t_4-t_3)\Bigr\}
U_{nk}(t_3)\exp\Bigl\{-i\frac{E_k}{\hbar}t_3\Bigr\}\\
&\quad =\left(-\frac{i}{\hbar}\right)^{2}\sum_n \int_{0}^{T}dt_4\int_{0}^{t_4}dt_3\,
\exp\Bigl\{-i\frac{E_l}{\hbar}(T-t_4)\Bigr\}
\left(-\frac{e}{mc}c\sqrt{\frac{2\pi\hbar}{\omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}\,e^{i\omega_2 t_4}\right)\\
&\qquad \times \exp\left\{-\frac{i}{\hbar}E_n(t_4-t_3)\right\}
\left(-\frac{e}{mc}c\sqrt{\frac{2\pi\hbar}{\omega_1}}\,(\mb{p}\cdot\mb{e}_1)_{nk}\,e^{-i\omega_1 t_3}\right)
\exp\left(-\frac{i}{\hbar}E_k t_3\right)
\end{align*}
従って,
\begin{align}
&\left(-\frac{i}{\hbar}\right)^{2}\left(-\frac{e}{mc}\right)^{2}\sum_n \frac{2\pi\hbar c^{2}}{\sqrt{\omega_1 \omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\notag\\
&\quad \times \int_{0}^{T}dt_4\int_{0}^{t_4}dt_3\,\exp\left[-i\frac{E_l}{\hbar}(T-t_4)+i\omega_2 t_4\right]
\exp\left[-i\frac{E_n}{\hbar}(t_4-t_3)-i\omega_1 t_3\right]\exp\left[-i\frac{E_k}{\hbar}t_3\right]
\tag{1.6.8}
\end{align}
&\left(-\frac{i}{\hbar}\right)^{2}\left(-\frac{e}{mc}\right)^{2}\sum_n \frac{2\pi\hbar c^{2}}{\sqrt{\omega_1 \omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\notag\\
&\quad \times \int_{0}^{T}dt_4\int_{0}^{t_4}dt_3\,\exp\left[-i\frac{E_l}{\hbar}(T-t_4)+i\omega_2 t_4\right]
\exp\left[-i\frac{E_n}{\hbar}(t_4-t_3)-i\omega_1 t_3\right]\exp\left[-i\frac{E_k}{\hbar}t_3\right]
\tag{1.6.8}
\end{align}
すなわち,
\begin{equation}
-\frac{e^{2}}{m^{2}\hbar} \sum_n \frac{2\pi}{\sqrt{\omega_1 \omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\,e^{-iE_l T/\hbar}\int_{0}^{T}dt_4\,e^{i(E_l-E_n+\hbar\omega_2)t_4/\hbar}
\int_{0}^{t_4}dt_3\,e^{i(E_n-E_k-\hbar\omega_1)t_3/\hbar}
\tag{1.6.8′}
\end{equation}
-\frac{e^{2}}{m^{2}\hbar} \sum_n \frac{2\pi}{\sqrt{\omega_1 \omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\,e^{-iE_l T/\hbar}\int_{0}^{T}dt_4\,e^{i(E_l-E_n+\hbar\omega_2)t_4/\hbar}
\int_{0}^{t_4}dt_3\,e^{i(E_n-E_k-\hbar\omega_1)t_3/\hbar}
\tag{1.6.8′}
\end{equation}
この積分は, 以前に検討した遷移確率での積分と同様であるから,
\begin{align*}
&-\frac{e^{2}}{m^{2}\hbar}\sum_n \frac{2\pi}{\sqrt{\omega_1\omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\,\,e^{-iE_l T/\hbar}\int_{0}^{T}dt_4\,e^{i(E_l-E_n+\hbar\omega_2)t_4/\hbar}\,
\frac{1-e^{i(E_n-E_k-\hbar\omega_1)t_4/\hbar}}{E_n-E_k-\hbar\omega_1}\\
&\quad \simeq \frac{e^{2}}{m^{2}\hbar}\sum_n \frac{2\pi}{\sqrt{\omega_1\omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\,\,e^{-iE_l T/\hbar}\frac{1}{E_n-E_k-\hbar\omega_1}
\int_0^{T}dt_4\,e^{i(E_l+\hbar\omega_2-E_k-\hbar\omega_1)t_4/\hbar}
\end{align*}
従って, 和は次のようになる：
\begin{equation}
\frac{e^{2}}{m^{2}}\sum_n \frac{2\pi}{\sqrt{\omega_1 \omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\,e^{i\phi}\,\frac{1}{E_n-E_k-\hbar\omega_1}\frac{1-e^{i\Delta T/\hbar}}{\Delta}
\tag{1.6.9}
\end{equation}
\frac{e^{2}}{m^{2}}\sum_n \frac{2\pi}{\sqrt{\omega_1 \omega_2}}\,(\mb{p}\cdot\mb{e}_2)_{ln}
(\mb{p}\cdot\mb{e}_1)_{nk}\,e^{i\phi}\,\frac{1}{E_n-E_k-\hbar\omega_1}\frac{1-e^{i\Delta T/\hbar}}{\Delta}
\tag{1.6.9}
\end{equation}
ただし \(\Delta=(E_l+\hbar\omega_2-E_k-\hbar\omega_1)\) であり, また位相角 \(\phi\) は \(n\) に依存しない．\((E_n-\hbar\omega_1-E_k)(E_l+\hbar\omega_2-E_n)\) で与えられる分母を持つ項は無視される．なぜなら前の第 4 講の式 (4.6) の結果から, 重要なのは \(E_l+\hbar\omega_2\approx E_k+\hbar\omega_1\) となるエネルギーだけだからである．最終結果は次のように書くことが出来る：
\begin{equation}
\mathrm{Trans.prob./sec}=\frac{2\pi}{\hbar}|M|^{2}\,\frac{\omega_2^{2}\,d\Omega_2}{(2\pi c)^{3}\hbar}
=d\sigma c
\tag{1.6.10}
\end{equation}
\mathrm{Trans.prob./sec}=\frac{2\pi}{\hbar}|M|^{2}\,\frac{\omega_2^{2}\,d\Omega_2}{(2\pi c)^{3}\hbar}
=d\sigma c
\tag{1.6.10}
\end{equation}
ただし \(|M|\) は \(\omega_2\) で積分し \(\mb{e}_2\) について平均化することにより \(A_{lk}\) から決定される．すると断面積 \(d\sigma\) の完全な表現式は次となる： [4]この式 (1.6.11) は「Kramers-Heisenberg 公式」と呼ばれ, J.J.Sakurai:「Advanced Quantum Mechanics」§ 2.5 の式 (2.162) に等価である．従って, 式の係数は Gauss … Continue reading
\begin{equation}
d\sigma = \frac{e^{4}}{m^{2}c^{4}}\,\frac{\omega_2}{\omega_1}\,d\Omega_2\,
\left|\frac{1}{m}\sum_n \left\{\frac{(\mb{p}\cdot\mb{e}_2)_{ln}(\mb{p}\cdot\mb{e}_1)_{nk}}{E_k+\hbar\omega_1-E_n}
+\frac{(\mb{p}\cdot\mb{e}_1)_{ln}(\mb{p}\cdot\mb{e}_2)_{nk}}{E_k-E_n-\hbar\omega_2}\right\}+
(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\right|^{2}
\tag{1.6.11}
\end{equation}
d\sigma = \frac{e^{4}}{m^{2}c^{4}}\,\frac{\omega_2}{\omega_1}\,d\Omega_2\,
\left|\frac{1}{m}\sum_n \left\{\frac{(\mb{p}\cdot\mb{e}_2)_{ln}(\mb{p}\cdot\mb{e}_1)_{nk}}{E_k+\hbar\omega_1-E_n}
+\frac{(\mb{p}\cdot\mb{e}_1)_{ln}(\mb{p}\cdot\mb{e}_2)_{nk}}{E_k-E_n-\hbar\omega_2}\right\}+
(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\right|^{2}
\tag{1.6.11}
\end{equation}
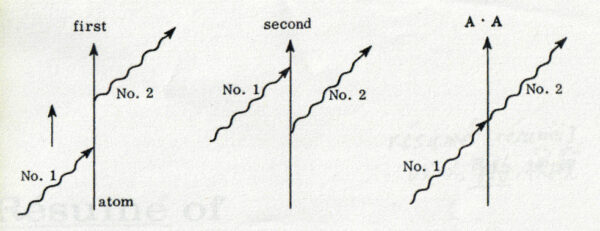
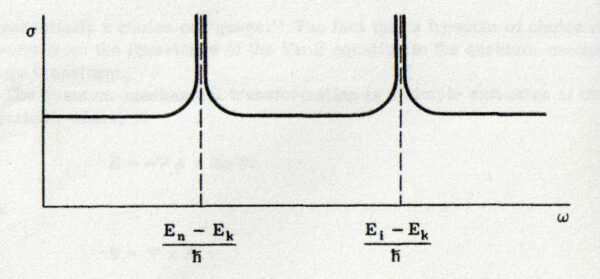
和中の第 1 項は先に述べた「第 1 項」に由来し, 第 2 項は「第 2 項」に由来する．絶対値の中の最後の項は, 最初の積分項に於ける \(\mb{A}\cdot\mb{A}\) すなわち \(c_l^{(1)}(T)\) に於いて \(U_{lk}(t_3)\) が, \[U_{lk}(t_3)=\frac{e^{2}}{2mc^{2}}(2\mb{A}_1\cdot\mb{A}_2)_{lk}\] である場合に由来している [5]【 補足 】 … Continue reading．
もし \(l\neq k\) ならば, 散乱は「非干渉性(incoherent)」であり, その結果は「Raman効果」と呼ばれる．もし \(l=k\) ならば, 散乱はコヒーレント(干渉性)である．
更に, 全ての原子が基底状態にあり \(l\ne k\) である場合, 原子のエネルギーは増加する一方であり, 光の周波数 \(\omega\) は減少する一方であることに注意すべし．これにより「Stokes線」が生じる．逆の効果は「反ストークス線」を生じる．
\(\omega_1=\omega_2\) (コヒーレント散乱) だが \(\hbar\omega_1\) は \(E_k-E_n\) にほぼ等しいと仮定しよう．このとき \(n\) についての和の中で 1 つの項が非常に大きくなり, 残りの項に対して支配的となる．この結果は「共鳴散乱」と呼ばれる．断面積 \(\sigma\) を \(\omega\) に対してプロットすると, このような \(\omega\) の値で \(\sigma\) は鋭い極大値を持つ (図6-3参照)．
図 6-3
気体の「屈折率」(index of refraction) は散乱公式によって求めることが出来る．他のタイプの散乱と同様に, それは前方方向に散乱された光を考慮することで求めることが出来る．
自己エネルギー(Self-Energy)
量子電気力学で考慮しなければならないもう一つの現象は, 原子が光子を放出し同じ光子を再吸収する可能性である．これは対角要素 \(A_{kk}\) に影響を与える．その効果はエネルギー準位のシフトに相当し,次式が成り立つ：
\begin{equation}
\Delta E = \sum_n \int \frac{(\mb{p}\cdot\mb{e})_{kn}(\mb{p}\cdot\mb{e})_{nk}}{E_k-E_n-\hbar\omega}
\frac{d^{3}\mb{K}}{(2\pi\hbar)^{3}}\frac{2\pi}{\omega}
\tag{1.6.12}
\end{equation}
\Delta E = \sum_n \int \frac{(\mb{p}\cdot\mb{e})_{kn}(\mb{p}\cdot\mb{e})_{nk}}{E_k-E_n-\hbar\omega}
\frac{d^{3}\mb{K}}{(2\pi\hbar)^{3}}\frac{2\pi}{\omega}
\tag{1.6.12}
\end{equation}
ただし \(\mb{e}\) は偏極方向である．この積分は発散する．より厳密な相対論的計算でも, 得られる積分は発散する．それは電磁気効果に関する我々の定式化が, 実際には完全に満足できる理論ではないことを意味している．自己エネルギーが無限大であるというこの難点を回避するために必要な修正については後述する．正味の結果はエネルギー準位の位置の非常に小さなシフト \(\Delta E\) である．このシフトは Lamb と Retherford によって観測された．
References
| ↑1 | ファインマン経路積分の § 6-5 より, 遷移振幅 \(\lambda_{mn}\) は次の式 (6-69), 式 (6-72), 式 (6-74) などで表すことが出来た： \begin{align*} \lambda_{mn}&=\delta_{mn}e^{-iE_n(t_2-t_1)/\hbar}+\lambda_{mn}^{\ (1)}+\lambda_{mn}^{\ (2)}+\dotsb,\tag{6-69}\\ \lambda_{mn}^{\ (1)}&=-\frac{i}{\hbar}e^{-iE_mt_2/\hbar}e^{+iE_nt_1/\hbar}\int_{t_1}^{t_2}dt_3\,V_{mn}(t_3) \,e^{i(E_m-E_n)t_3/\hbar},\tag{6-72}\\ \lambda_{mn}^{\ (2)}&=-\reverse{\hbar^{2}}\int_{t_1}^{t_2}dt_4\int_{t_1}^{t_4}dt_3\,\sum_{k} e^{-iE_m(t_2-t_4)/\hbar}\,V_{mk}(t_4)\,e^{-iE_k(t_4-t_3)/\hbar}\,V_{kn}(t_3)\,e^{-iE_n(t_3-t_1)/\hbar}, \tag{6-74} \end{align*} 以上の式で \(n\to k,m\to l,k\to n,V=U\)とし, 時間を \(t_1=0,t_2=T\) としたものが式 (1.6.5)である． |
|---|---|
| ↑2 | スピンを無視するので, 第3講の式 (3.11) の第 3 項は含めない．そのときの摂動 \(U\)は 次となる： \begin{equation*} \Delta H =-\frac{e}{2mc}(\mb{p}\cdot\mb{A}+\mb{A}\cdot\mb{p})+\frac{e^{2}}{2mc^{2}}\mb{A}\cdot\mb{A} \end{equation*} ただし \(\mb{p}\cdot\mb{A}\) のような形で現れる演算子 \(\mb{p}\) はその右側の全てに作用する微分演算子であるが,「横波条件」 \(\nabla\cdot\mb{A}=0\) を想定するので \(\mb{p}\cdot\mb{A}\) を \(\mb{A}\cdot\mb{p}\) に置き換えることが許される．従って, \begin{equation*} \Delta H = e^{i\omega t}\,U=-\frac{e}{2mc}(\mb{A}\cdot\mb{p}+\mb{A}\cdot\mb{p})+\frac{e^{2}}{2mc^{2}}\mb{A}\cdot\mb{A} =-\frac{e}{mc}\mb{A}\cdot\mb{p}+\frac{e^{2}}{2mc^{2}}\mb{A}\cdot\mb{A} \end{equation*} |
| ↑3 | 入射光子の吸収と光子の放射が起こらねばならないので, 遷移振幅を表す項には入射光子を表わす \(\mb{A}_1\) と放射光子を表わす \(\mb{A}_2\) が 1 個ずつ因子となっているべきである．式 (1.6.6) の第 1 項では \begin{equation*} -\frac{e}{mc}\mb{A}\cdot\mb{p}=-\frac{e}{mc}(\mb{A}_1+\mb{A}_2)\cdot\mb{p} =-\frac{e}{mc}\mb{A}_1\cdot\mb{p}+-\frac{e}{mc}\mb{A}_2\cdot\mb{p} \end{equation*} となるので, 各項に \(\mb{A}_1\) と \(\mb{A}_2\) ともに現れることはない．しかし第 2 項では, \begin{equation*} +\frac{e^{2}}{2mc}\mb{A}\cdot\mb{A}=\frac{e^{2}}{2mc}(\mb{A}_1+\mb{A}_2)\cdot(\mb{A}_1+\mb{A}_2) =\frac{e^{2}}{2mc}(\mb{A}_1\cdot\mb{A}_1+\mb{A}_2\cdot\mb{A}_2+2\mb{A}_1\cdot\mb{A}_2) \end{equation*} となるので, この第 3 項目の交差項 \(2\mb{A}_1\cdot\mb{A}_2\) では \(\mb{A}_1\) と \(\mb{A}_2\) が 1 個ずつ因子として含まれる． |
| ↑4 | この式 (1.6.11) は「Kramers-Heisenberg 公式」と呼ばれ, J.J.Sakurai:「Advanced Quantum Mechanics」§ 2.5 の式 (2.162) に等価である．従って, 式の係数は Gauss 有理化単位系に於ける「古典電子半径」 \(r_0\) の 2 乗である： \begin{equation*} r_0^{2}=\frac{e^{4}}{m^{2}c^{4}},\quad r_0=\frac{e^{2}}{m c^{2}}=\frac{e^{2}}{\hbar c}\frac{\hbar}{mc}=\alpha\frac{\hbar}{mc}\simeq \frac{1}{137}\frac{\hbar}{mc}\simeq 2.82\times 10^{-13}\ \mathrm{cm} \end{equation*} |
| ↑5 | 【 補足 】 \(c_l^{(1)}(T)\)を具体的に計算してみる： \begin{equation*} c_{l}^{(1)}(T)=-\frac{i}{\hbar}\int_0^{T}dt_3\,U_{lk}(t_3)\,e^{i(E_l-E_k)t_3/\hbar},\quad U_{lk}(t_3)=\frac{e^{2}}{2mc^{2}}\int \phi_l^{*}(\mb{x})\,2\mb{A}_1\cdot\mb{A}_2^{*}\,\phi_k(\mb{x})\,d\mb{x} \end{equation*} まず行列要素 \(U_{lk}(t_3)\) を計算する．式 (1.6.4) から, \begin{align*} U_{lk}(t_3)&=\frac{e^{2}}{mc^{2}}\int \phi_l^{*}(\mb{x})\,\sqrt{\frac{2\pi\hbar c^{2}}{\omega_1}}\,\mb{e}_1\, e^{-i(\omega_1 t_3-\mb{K}\cdot\mb{x})}\cdot \sqrt{\frac{2\pi\hbar c^{2}}{\omega_2}}\,\mb{e}_2\, e^{i(\omega_2 t_3-\mb{K}\cdot\mb{x})}\,\phi_k(\mb{x})\,d^{3}\mb{x}\\ &=\frac{e^{2}}{m}\frac{2\pi\hbar}{\sqrt{\omega_1\omega_2}}(\mb{e}_1\cdot\mb{e}_2)\,e^{i(\omega_2-\omega_1)t_3} \int \phi_l^{*}(\mb{x})\phi_k(\mb{x})\,d^{3}\mb{x}\\ &=\frac{e^{2}}{m}\frac{2\pi\hbar}{\sqrt{\omega_1\omega_2}}(\mb{e}_1\cdot\mb{e}_2)\,e^{i(\omega_2-\omega_1)t_3}\, \delta_{lk} \end{align*} 従って \(c_l^{(1)}(T)\) は, \begin{align*} c_{l}^{(1)}(T)&=-\frac{i}{\hbar}\int_0^{T}dt_3\,\frac{e^{2}}{m}\frac{2\pi\hbar}{\sqrt{\omega_1\omega_2}} (\mb{e}_1\cdot\mb{e}_2)\,e^{i(\omega_2-\omega_1)t_3}\,\delta_{lk}\,e^{i(E_l-E_k)t_3/\hbar}\\ &=\frac{e^{2}}{m}\frac{2\pi\hbar}{\sqrt{\omega_1\omega_2}}(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk} \left(-\frac{i}{\hbar}\int_0^{T}dt_3\,e^{i(\omega_2-\omega_1)t_3}\right)\\ &=\frac{e^{2}}{m}\frac{2\pi}{\sqrt{\omega_1\omega_2}}(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk} \frac{1-e^{i(\omega_2-\omega_1)T}}{\omega_2-\omega_1} \end{align*} すると \(|c_l^{(1)}|^{2}\) は, \begin{align*} \bigl|c_l^{(1)}(T)\bigr|^{2}&=\frac{e^{4}}{m^{2}}\frac{(2\pi)^{2}}{\omega_1\omega_2}\bigl|(\mb{e}_1\cdot\mb{e}_2)\, \delta_{lk}\bigr|^{2}\frac{\sin^{2}(\omega_2-\omega_1)T/2}{(\omega_2-\omega_1)^{2}}\\ &=\frac{e^{4}}{m^{2}}\frac{(2\pi)^{2}}{\omega_1\omega_2}\bigl|(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\bigr|^{2} \pi T \delta\left\{\frac{1}{2}(\omega_2-\omega_1)\right\}\\ &=T\frac{e^{4}}{m^{2}}\frac{(2\pi)^{3}}{\omega_1\omega_2}\bigl|(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\bigr|^{2} \delta(\omega_2-\omega_1) \end{align*} よって, 単位時間当りの遷移確率は \(T=1\) とし, 式 (1.2.7) から, \begin{align*} P_{lk}\,d\Omega_2&=\bigl|c_l^{(1)}(T)\bigr|^{2}\,\frac{\omega_2^{2}d\Omega}{(2\pi)^{3}c^{3}\hbar} =\frac{e^{4}}{m^{2}}\frac{(2\pi)^{3}}{\omega_1\omega_2}\bigl|(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\bigr|^{2} \delta(\omega_2-\omega_1)\,\frac{\omega_2^{2}d\Omega}{(2\pi)^{3}c^{3}\hbar}\\ &=\frac{e^{4}}{m^{2}c^{3}\hbar}\frac{\omega_2}{\omega_1}\bigl|(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\bigr|^{2} \delta(\omega_2-\omega_1)\,d\Omega_2=\sigma c\,d\Omega_2 \end{align*} よって散乱角 \(\sigma\) で表すならば, \begin{equation*} \sigma\,d\Omega_2=\frac{e^{4}}{m^{2}c^{4}\hbar}\frac{\omega_2}{\omega_1} \bigl|(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\bigr|^{2}\delta(\omega_2-\omega_1)\,d\Omega_2 =\frac{e^{4}}{m^{2}c^{4}\hbar}\bigl|(\mb{e}_1\cdot\mb{e}_2)\bigr|^{2}\,d\Omega_2 \end{equation*} ただし公式ではデルタ関数をエネルギー領域で考えているから, デルタ関数 \(\delta(\omega_2-\omega_1)\) をエネルギーで表現すると, \begin{equation*} \delta(\omega_2-\omega_1)=\delta\left\{\frac{1}{\hbar}(\hbar\omega_2-\hbar\omega_1)\right\} =\hbar\,\delta(E_2-E_1) \end{equation*} よって, \begin{equation*} d\sigma=\frac{e^{4}}{m^{2}c^{4}}\frac{\omega_2}{\omega_1}\,d\Omega_2\, \bigl|(\mb{e}_1\cdot\mb{e}_2)\,\delta_{lk}\bigr|^{2}\,\delta(E_2-E_1) =\frac{e^{4}}{m^{2}c^{4}}\bigl|(\mb{e}_1\cdot\mb{e}_2)\bigr|^{2}\,d\Omega_2 \end{equation*} これが式 (1.6.11) の絶対値中の最後の項に相当するものである．この断面積の式は, 自由電子(非束縛電子) による光の散乱と同じものになり, \(\omega\) に依存しないことに注意する．この式は, 最初は古典的な手続きに基づいて J.J.Thomson が与えたので,「Thomson散乱」(光子-電子散乱) と呼ばれる散乱の断面積の式となっている． |
