特殊相対論では動く物体は縮むのでなく回転して見える！

今年度のノーベル物理学賞受賞者の一人にロジャー・ペンローズ卿がいる．彼に興味を持ったので, 竹内薫著「ペンローズのねじれた４次元」を読んでいる．その第１章「あるけど見えないローレンツ収縮」の中に次のような記述があった：

相対性理論では, 動いている物体は縮んで見える？否！
ローレンツ変換で概念的に物体が縮むのは視線方向なので, 物体の実際の見え方には影響しない．確かに, 目の前を右から左に飛んで行く物体は縮むのだが, 物体の頭とお尻から私の目に届く光は, 同時に発せられたものではないため, 視覚的には, 物体は＜縮む＞のではなく, ＜回転＞して見える．つまり, 本来は見えないはずの物体の後ろ姿がちらっと見える．この驚くべき現象を世界で初めて証明したのが, われらがペンローズ卿であった．

興味を持ったので, ネットで関係する論文を読んで見ようとしたが, ベンローズ卿の原文は入手出来なかった．そこで代わりに, 下記のリンク先にある Dr. Daniel Weiskopf の学位論文の第２章と第４章を翻訳してみたので下記に提示しておく．

https://publikationen.uni-tuebingen.de/xmlui/bitstream/handle/10900/48159/pdf/01dissertation.pdf

また, 「python」と「Asymptote」を用いたプログラミングによって, 物体の実際の見え方を視覚的に提供しているサイトがあった：

visual appearance of a moving object in special relativity

ここには、見え方をアニメーション化したプログラムも含まれているので実際に実行してみると楽しい．
このサイトの元になった論文は次である：

visual appearance in special relativity

参考のために、この論文も翻訳してみた：

translation of visual appearance

\(\)

Visualization of Four-Dimentional Spacetimes
1. ２特殊相対性理論の可視化序論
  1. 2.1 歴史的な備考
2. 4 特殊相対論的視覚化の物理的基礎

Visualization of Four-Dimentional Spacetimes

Daniel Weiskopf

２特殊相対性理論の可視化序論

2.1 歴史的な備考

驚くべきことに, 特殊相対性理論における視覚の問題は長い間無視されていたか, 間違った解釈が与えられていた．アインシュタインは, 特殊相対性理論についての原論文の中で次のように書いている：

静止状態では球体の形で測定される剛体は, 運動状態では静止系から見ると軸を中心とした回転楕円体の形をしているように見える．よって球体 (そして任意形状の剛体) の Y 次元と Z 次元は, 運動によって変更されていないように見えるのに対し, X 次元は \(1:\sqrt{1-(v/V)^{2}}\) の比率で短縮されているように, すなわち, 値 \(v\) が大きいほど短縮化の度合いは大きくなるように見える．

「見ること」と「測定すること」の違いは非常に重大である．「測定」は, 観察者の基準座標に対し同時に全ての適切なサンプル地点に於いて行われる．しかし,「見ること」は, 観察者のカメラに同時に到達する光子に基づいている．これらの光子は, 通常では光速度の有限性のために (観察者の基準座標に対して) 同時には放出されていない．アインシュタインは論文の中で「betrachtet」(見る,見なす,考える) と「erscheinen」(見える) という言葉を使っており, それゆえ,「見ること」と「測定すること」の違いを明確に表現してはいない．しかしながら, 相対性理論に於ける視覚の知覚について間違った説明をしている出版物もある．例えば、 Gamow は彼の著書『不思議の国のトムキンス』の中で,「ローレンツ収縮」と「運動物体の視覚」を同一視している．
Lampaは, 1924年に「ローレンツ収縮は見えない」ことについて論文を書いたが無視された．それを除くと, 特殊相対論に於ける視覚的な知覚の問題について最初の正しい解決を与えたのは, やっと1959年に Penrose と Terrell によって提示されたに過ぎない．その後, 高速で運動する物体の幾何学的な見え方のより詳しい記述が Weisskopf, Boas, Scott, そして Viner によって与えられた．これらの論文は, 以下で述べる「高速で運動する物体の見え方」の基礎的な性質を導出し説明した．「通常, これらの物体は収縮しているようには見えず, むしろ回転し, そして歪んでいるように見える．直線では, それが進行方向に垂直な場合は双曲線のように見えるが, 進行方向に平行な場合は直線のままであるように見える」．

4 特殊相対論的視覚化の物理的基礎

4.1 ローレンツ変換

ローレンツ変換は二つの基準座標を関係付ける．それは特殊相対論の基礎的な要素である．時間座標 \(t\) と３つの空間座標 \((x,y,z)\) は結びついて位置の 4-ベクトルを形成し「時空」中の点を記述する：

\begin{equation}
x^{\mu}=\big(t,x,y,z\big)=\big(x^{0},x^{1},x^{2},x^{3}\big),\quad \mu=0,1,2,3.
\tag{4.1}
\end{equation}

ただし, これ以降では光速度 \(c\) を \(1\) とする単位系を用いる．線分要素は次となる：

\begin{equation}
ds^{2}=dt^{2}-dx^{2}-dy^{2}-dz^{2}=\eta_{\mu\nu}dx^{\mu}dx^{\nu}
\tag{4.2}
\end{equation}

ギリシャ文字の添字は集合 \(\{0,1,2,3\}\) からとなる．アインシュタインの和の規則が用いられる．「ミンコフスキー計量」 (Minkowski metric) は次である：

\begin{equation}
\eta_{\mu\nu}=\left(\begin{array}{@{\,}cccc@{\,}}
1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{array} \right)
\tag{4.3}
\end{equation}

「ローレンツ変換」(Lorentz transformation) は, ミンコフスキー座標の同次な線形変換である：

\begin{equation}
x^{\mu}\mapsto x’^{\mu}=\Lambda^{\mu}_{\ \nu} x^{\nu}
\tag{4.4}
\end{equation}

これは計量 \(\eta_{\mu\nu}\) を不変に保つ．前式から次となる：

\begin{equation}
\def\mf#1{\mathrm{#1}}
\def\mb#1{\mathbf{#1}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\Lambda^{\mu}_{\ \nu}= \ppdiff{x’^{\mu}}{x^{\nu}}
\tag{4.5}
\end{equation}

逆ローレンツ変換は次となる：

\begin{equation}
x’^{\mu}\mapsto x^{\mu}=\Lambda^{\ \mu}_{\nu} x’^{\nu},\quad \text{with}\quad
\Lambda^{\ \mu}_{\nu}=\ppdiff{x^{\mu}}{x’^{\nu}}
\tag{4.6}
\end{equation}

ローレンツ変換はローレンツ群 \(L\) を形成する．\(L\) は \(\mf{det}\Lambda^{\mu}_{\ \nu}=\pm1\) 及び \(\Lambda^{0}_{\ 0}\ge +1\) か \(\le -1\) によって4個の組に分類される．この論文の残りの部分では,「本義 (proper) ローレンツ変換」 \((\mf{det}\Lambda^{\mu}_{\ \nu}=1)\) で「順時( orthochronous) ローレンツ変換」 \((\Lambda^{0}_{\ 0}\ge 1)\) である変換 \(L^{\uparrow}_{+}\) だけを考える．変換 \(L^{\uparrow}_{+}\) は, 空間的な向きと時間の向きを保存する変換である．ローレンツ変換は２つの基準慣性系を結び付け, そして光の速度を不変に保つ変換である．ローレンツ変換は関係する慣性系の間での座標系の変更と見做すことが出来る．
ポアンカレ群は \(\eta_{\mu\nu}\) を不変のままとする非同次な線形変換を形成する．ローレンツ変換は基準座標系の平行移動を含めることでポアンカレ変換に拡張される：

\begin{equation}
x^{\mu}\mapsto x’^{\mu}=\Lambda^{\mu}_{\ \nu} x^{\nu}+a^{\mu}
\tag{4.7}
\end{equation}

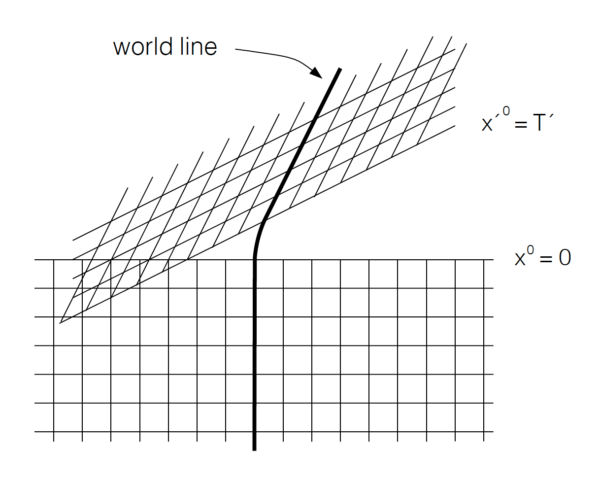
図 1 は, ポアンカレ変換をミンコフスキー図の形で幾何学的に示したものである．この場合のミンコフスキー図は, 座標 \(y\) と \(z\) を除いた時空図である．

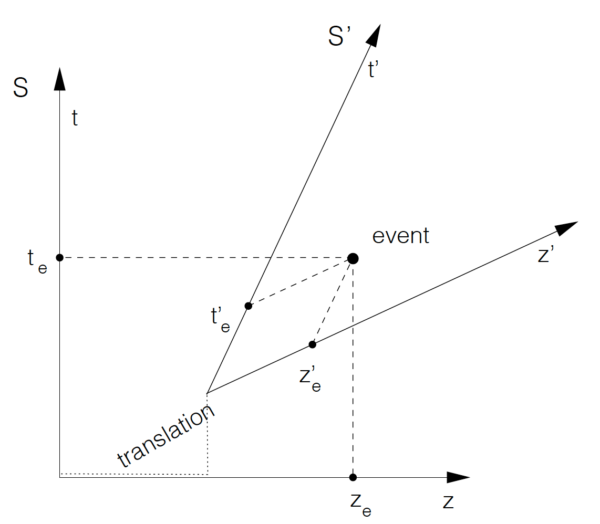
図 1. ミンコフスキー図は, 2つの基準座標系 \(S\) と \(S’\) を示している．二つの座標系の原点の平行移動 (translation) は明示的に印されている．基準座標系が異なる速度を持つために \(S’\) の座標軸の回転が起こる．ミンコフスキー図が示している空間は一次元だけなので, 空間での回転は考えない．事象を座標軸へ射影すると, 二つの基準座標中の事象 \((t_e,z_e)\) と \((t’_e,z’_e)\) となる．これがポアンカレ変換の幾何学的な解釈である．

一般的に, ４-ベクトルはローレンツ変換での特性によって定義される．反変な４-ベクトルは座標系毎に関係する4成分を持ち, それらは位置座標 \((x^{0},x^{1},x^{2},x^{3})\) と同じ仕方で変換する量として定義される．すなわち, 式(4.4)から,

\begin{equation}
b’^{\mu}=\Lambda^{\mu}_{\ \nu} b^{\nu}
\tag{4.8}
\end{equation}

共変な４-ベクトル \(a_{\mu}\) は次式に従って変換される：

\begin{equation}
a’_{\mu}=\Lambda_{\mu}^{\ \nu} a_{\nu}
\tag{4.9}
\end{equation}

２つの４-ベクトル間の内積は「ローレンツ不変」すなわち, ローレンツ変換の下で不変である：

\begin{equation}
a^{\mu}b_{\mu}=\eta_{\mu\nu}a^{\mu}b^{\nu}=\eta^{\mu\nu}a_{\nu}b_{\mu}=a_{\mu}b^{\mu}
\tag{4.10}
\end{equation}

４-ベクトルは, その長さの2乗 \(a^{\mu}a_{\mu}\) によって特徴付けられる．長さの２乗が負の場合, その４-ベクトルは「空間的」 (spacelike) であり, 長さの2乗が正の場合は「時間的」(timelike), そして長さの2乗がゼロの場合は「光的」(lightlike) である．「固有時」(proper time) は, 一緒に運動している時計によって測定される時間と定義される．固有時の微分はローレンツ-スカラーである：

\begin{equation}
d\tau=\frac{dt}{\gamma}=\sqrt{1-\beta^{2}}\,dt
\tag{4.11}
\end{equation}

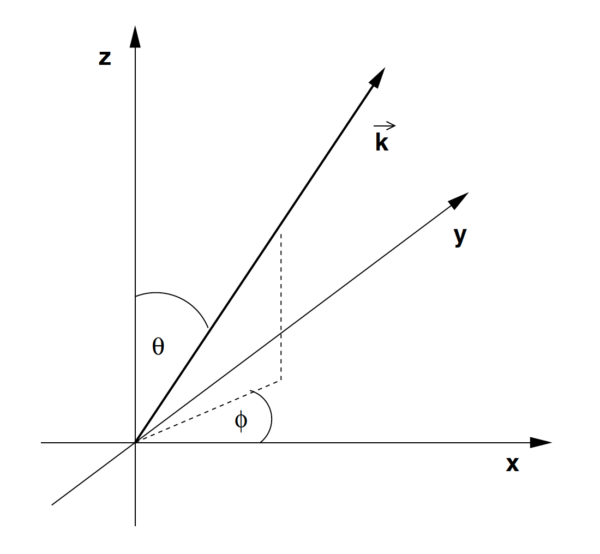
速度のパラメータたちは次で定義される：

\begin{equation}
\beta=\frac{v}{c}=v,\quad \gamma=\frac{1}{\sqrt{1-\beta^{2}}},
\tag{4.12}
\end{equation}

ただし \(v\) は速度の絶対値である．古典力学的な３次元速度は一般化されて４次元速度となる：

\begin{equation}
u^{\mu}=\frac{dx^{\mu}}{d\tau}=\frac{dx^{\mu}}{dt}\frac{dt}{d\tau}=\gamma\frac{dx^{\mu}}{dt}
\tag{4.13}
\end{equation}

４-速度 \(u^{\mu}\) は, 次式によって古典力学的な速度 \(\vec{v}=(v_x,v_y,v_z)\) と結び付いている：

\begin{equation}
u^{\mu}=\big(u^{0},u^{1},u^{2},u^{3}\big)=\gamma\big(1,v_x,v_y,v_z\big)
\tag{4.14}
\end{equation}

従って, ４-加速度 \(a^{\mu}\) は次となる：

\begin{equation}
a^{\mu}=\frac{du^{\mu}}{d\tau}=\frac{d^{2}x^{\mu}}{d\tau^{2}}
\tag{4.15}
\end{equation}

ローレンツ変換は, ２つの基準座標系の離別速度及び回転のパラメータに依存する．ポアンカレ変換では, さらに平行移動に対するパラメータが付加する．離別速度 (separating velocity) によるローレンツ変換は「ローレンツ-ブースト」(推進 Lorentz boost )と呼ばれる．一般的なローレンツ-ブーストは対称行列 \(\Lambda^{\mu}_{\ \nu}\) で定義される．その成分は次である：

\begin{equation}
\Lambda^{0}_{\ 0}=\gamma,\quad \Lambda^{0}_{\ j}=\Lambda^{j}_{\ 0}=-\beta \gamma n^{j},\quad
\Lambda^{j}_{\ k}=\Lambda^{k}_{\ j}=(\gamma-1)n^{j}n^{k}+\delta^{jk},
\tag{4.16}
\end{equation}

ただし \(\vec{n}=(n^{1},n^{2},n^{3})\) は規格化された運動方向ベクトル, \(\delta^{jk}\) はクロネッカー記号, そして \(j,k\in\{1,2,3\}\) である．回転は非相対論的な 3次元の場合で計算することが出来る．時空での平行移動は通常の 3次元空間での平行移動に類似し, 基礎に置くのは成分の付加である．

4.2 光の収差とドップラー効果

ローレンツ変換を光子の方向と波長に適用すると,「相対論的な光の収差とドップラー効果」 ( relativistic aberration of light and the Doppler effect ) が得られる．一つの基準座標系から別の基準座標系へ変えるとき, 相対論的な光の収差が光の向きを回転させる．光の収差は, 高速で動くカメラに映る見かけの幾何のまったく十分な完全記述である．図 2 は, 光の収差を図示したものである．ドップラー効果は, 一つの基準座標系から別の基準座標系へ波長を変換するために起き,　光の色を変化させる．光子の振動数と伝搬方向は, 次の４-波数ベクトルによって記述される：

\begin{equation}
k^{\mu}=\big(\omega,\vec{k}\big)
\tag{4.17}
\end{equation}

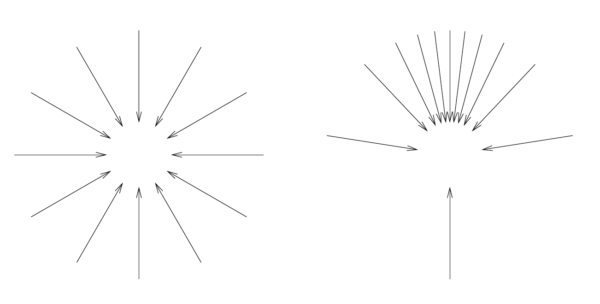
図 2. 光の相対論的収差．左の画像は静止した観測者によって記録されるいくつかの光線を示している．右の画像は同じ光線を上方向に \(\beta=0.9\) で運動する観測者が記録する場合を示している．動く観測者が受ける光線は前方ほどその視野角度は狭くなっているので, 前方部ほど遠くに見える．

波面に直交する３次元波数ベクトル \(\vec{k}\) は伝搬方向を指し, 光子の波長を \(\lambda\) として \(k=2\pi\lambda^{-1}\) の長さを持つ．角振動数 \(\omega\) は, 光子の振動数 \(\nu\) と \(\omega=2\pi\nu\) の関係を有する．波長と振動数の関係は \(\lambda=c/\nu=1/\nu\) である．考慮するのは, 真空中の光伝搬だけである．
２つの慣性系 \(S\) と \(S’\) を考え, 系 \(S’\) は速度 \(v\) で系 \(S\) の \(z\) 軸の方向に動いているとしよう．\(z\) 軸方向のローレンツ変換が系 \(S\) と系 \(S’\) を結び付ける．基準座標系 \(S\) に於いて, 角振動数 \(\omega\) でその方向が図 3 に示すように極座標 \((\theta,\phi)\) で決定される光子を考える．各々の４-波数ベクトルは次である：

\begin{equation}
k^{\mu}=\big(\omega,\,\omega\cos\phi\sin\theta,\,\omega\sin\phi\sin\theta,\,\omega\cos\theta \big)
\tag{4.18}
\end{equation}

図 3. 波数ベクトル \(\vec{k}\) を持つ光子．

系 \(S’\) での４-波数ベクトルは, ローレンツ変換によって得られる．更に, 系 \(S’\) での光子は, 角運動量 \(\omega’\) と方向 \((\theta’,\phi’)\) によって記述される．２つの公式を比較することで, 光の相対論的な収差に対する表現式を読み取ることが出来る：

\begin{equation}
\cos\theta’=\frac{\cos\theta-\beta}{1-\beta\cos\theta},\quad \phi’=\phi,
\tag{4.19}
\end{equation}

そしてドップラー効果に対する式は次となる：

\begin{equation}
\omega’=\frac{\omega}{D}
\tag{4.20}
\end{equation}

ドップラー効果因子 \(D\) は次で定義される：

\begin{equation}
D=\frac{1}{\gamma\big(1-\beta\cos\theta\big)}=\gamma\big(1+\beta\cos\theta’\big)
\tag{4.21}
\end{equation}

ドップラー効果を波長で表現すると次となる：

\begin{equation}
\lambda’=D\lambda
\tag{4.22}
\end{equation}

4.3 サーチライト効果

サーチライト効果の基礎は, 放射を一つの基準座標系から別の基準座標系へ変換することである．式 (4.19) より, 動く物体から放射される光は運動方向に向かって円錐状に収束する．これを「相対論的ビーミング」(relativistic beaming )　という．従って,　観測者が高速度で物体に近づくとき,　その物体の前方の明るさは放射の変換によって増大する．

4.3.1 放射輝度の変換

観測方向に垂直な放射源の単位面積が観測方向の単位立体角内に放出する放射束を「放射輝度」(radiance ) という．周波数-依存の放射輝度 \(L_{\nu}\) は, 次式により一つの基準座標系から別の基準座標系へ変換する．

\begin{equation}
L’_{\nu} (\nu’,\theta’,\phi’)=\frac{1}{D^{3}}L_{\nu}(\nu,\theta,\phi).
\tag{4.23}
\end{equation}

同様に, 波長-依存の放射輝度 \(L_{\lambda}\) は, 次式に従って変換する：

\begin{equation}
L’_{\lambda} (\lambda’,\theta’,\phi’)=\frac{1}{D^{5}}L_{\lambda}(\lambda,\theta,\phi).
\tag{4.24}
\end{equation}

全ての波長に亘って積分することで, 放射輝度 \(L\) の写像(変換) が得られる：

\begin{equation}
L'(\theta’,\phi’)=\frac{1}{D^{4}}L(\theta,\phi).
\tag{4.25}
\end{equation}

4.3.2 点光源からの入射放射度

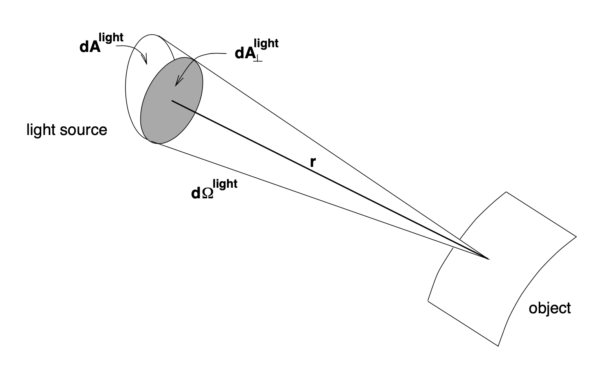
単位時間に単位面積に入射する放射エネルギーを「放射度」(irradiance ) という．物体表面の小区画(patch) に対して, 運動している点光源からやって来る放射の波長-依存の放射度 \(E^{i’}_{\lambda}(\lambda’)\) は次となる：

\begin{equation}
E^{i’}_{\lambda}(\lambda’)=\frac{1}{D^{5}}\frac{\cos\alpha’}{r’^{2}}I_{\lambda}(\lambda)
\tag{4.26}
\end{equation}

ただし表面に垂直なベクトルと入射光子の方向の角度を \(\alpha’\) とし, 光源と表面部分の見かけの距離を \(r’\) とする．これらの量は, 運動する観測者の基準座標系から測定されるとするが, 波長-依存の強度 \(I_{\lambda}\) は光源の基準座標系で測定されるとする．従って, 周波数-依存の放射度は,

\begin{equation}
E^{i’}_{\nu}(\nu’)=\frac{1}{D^{3}}\frac{\cos\alpha’}{r’^{2}}I_{\nu}(\nu)
\tag{4.27}
\end{equation}

これを積分することで, 波長-依存しない放射度は次となる：

\begin{equation}
E^{i’}(\nu’)=\frac{1}{D^{4}}\frac{\cos\alpha’}{r’^{2}}I
\tag{4.28}
\end{equation}

一方の基準座標系で等方性の点光源である場合, ドップラー因子 \(D\) の暗黙の角度依存性により, 他方の基準座標系では異方性の点光源が得られることに注意すべし．なお, 放射輝度と放射度の導出は付録に示してある (省略する)．

4.4 光子の場の変換

相対性理論の原理により, 全ての基準慣性系は物理的なシナリオを記述するのには同様に有効である．従って, 各々の用途に最適な慣性系を選択することが出来る．特殊相対論的な映像(image) を計算する場合, 観測者が高速に動く状態で静止シーンを考えることも出来るし, または物体が高速に動く状態で静止したカメラを考えることも出来る．最初の場合を「外心的風景」(exocentric view ) と名付ける．なぜなら, カメラの外にある系を基準座標系として採用しているからである．
外心構造的な研究法は以下のように行う．最初のステップは, 座標系の外側に関する全ての「照度」(illumination ) 計算を行うことである．照度とは「単位面積当たりの光束」であり, 単位は lux である．次のステップは, 観測者に届く光の関係情報を, 観測者の系に変換することである．この情報は, いわゆる「plenoptic function」によって提示される．全プレノプティク関数 \(P(x,y,z,t,\theta,\phi,\lambda)\) は, 極座標での方向 \((\theta,\phi)\) に依存する光の放射輝度 \(L\), 空間位置 \((x,y,z)\), 時間 \(t\), そして波長 \(\lambda\) の関数である．偏極は通常は無視される．プレノプティク関数は, 光子場に関係する情報をコンパクトに表現したものである．縮小した３-パラメーターのプレノプティク関数 \(\tilde{P}(\theta,\phi,\lambda)\) は, 全プレノプティクス関数を位置 \((x,y,z)\) と時間 \(t\) で評価したものとして定義される．

4.4.1 プレノプティクス関数の変換

縮小プレノプティクス関数 \(\tilde{P}\) の変換は, 相対論的な光収差, ドップラー効果, そしてサーチライト効果によって決定される．これらの効果は一緒になって \(S\) から \(S’\) へのプレノプティクス関数の変換を形成する：

\begin{equation}
\tilde{P}(\theta’,\phi’,\lambda’)=\frac{1}{D^{5}}\tilde{P}(\theta,\phi,\lambda)
=\frac{1}{D^{5}}\tilde{P}\left(\arccos\frac{\cos\theta’+\beta}{1+\beta\cos\theta’},\phi’,\frac{\lambda’}{D}
\right)
\tag{4.29}
\end{equation}

式 (4.19) と式 (4.20) の逆演算をすると, パラメーター \(\theta\), \(\phi\), \(\lambda\) は \(\theta’\), \(\phi’\), \(\lambda’\) を含む項で入れ替えることが出来る．通常, 運動の方向は \(z\)-方向に一致してはいない．従って更に, 収差変換の前後で座標系の回転を考える必要がある．その回転は 3次元ユークリッド空間の通常の回転と同じである．この回転を含めると, 縮小プレノプティクス関数の完全なローレンツ変換が得られる．変換されたプレノプティクス関数 \(\tilde{P}’\) が依存するのは, 元のプレノプティクス関数 \(\tilde{P}\) と観測者が運動する速さとその方向のみであることに注意する．全プレノプティクス関数 \(P\) のローレンツ変換の場合, プレノプティクス関数を計算する各々の４-位置は, ポアンカレ変換によって関係付けなければならない．

4.5 事象に対する座標間の関係

相対論的映像を記述する別の方法は２つの基準座標系の間での発光事象(emisson event) の変換を基礎にするものである．それには「座標間の関係」(inter-frame relationship ) を利用する．
相対論的な観測者によって撮られるスナップ写真の作成について考察してみよう．映像作成時に, 観測者は基準座標系 \(S\) に対して速度 \(\vec{v}=(v_x,v_y,v_z)\) で動いている．\(S\) は外部世界の座標系である．座標系 \(S’\)は観測者の静止系であり, 従って観測者と共に \(S\) に対して速度 \(\vec{v}\) で動いている．系 \(S\) に静止している一点光源を考える．図４は, そのときのミンコフスキー図である．線分 \(\{(t,x_e,y_e,z_e)|t\}\) は点光源の世界線を表している．\(E\) で表されているのは, 過去光円錐と光源の世界線との交点である．\(E\) は, 点 \(O\) にいる観測者に到着する光の発光４-位置(emisson four-position) である．発光事象 \(E\) と吸収事象 \(O\) は光的な結び付きで関係している．４-ベクトルで表すならば, この事実すなわち「両者が交差する位置では世界距離がゼロとなっていること」は次式で表現される：

\begin{equation}
\big(x^{\mu}_{o} -x^{\mu}_{e}\big)\big(x_{o\nu}-x_{e\mu}\big)=0
\tag{4.30}
\end{equation}

ただし \(x^{\mu}_e\) は \(E\) の座標を, そして \(x^{\mu}_o\) は系 \(S\) 中の \(O\) の座標を表している．一旦, 過去光円錐と光源の世界線との交点が決定されると, 系 \(S’\) での \(E\) の座標を計算することが可能である．ミンコフスキー図中では, 点線で示されているようにグラフィカルに行うことが出来る．
それは \(S\) から \(S’\) へのポアンカレ変換に相当している．系 \(S\) では, 事象 \(E\) の時間座標は式 (4.30) を用いて計算することが出来る：

\begin{equation}
\big(x^{0}_{o}- x^{0}_{e}\big)=\sqrt{\big(x^{1}_{o}- x^{1}_{e}\big)+\big(x^{2}_{o}- x^{2}_{e})+(x^{3}_{o}- x^{3}_{e}\big)}
\tag{4.31}
\end{equation}

因果律が根号の正符号だけを選ぶことを要求する．すなわち, 過去光円錐との交点だけが考慮されて, 未来光円錐との交点は無視される．ポアンカレ変換を用いると, そのときの系 \(S’\) での発光事象の座標を計算することが出来る．

図 4. 観測者の座標系 \(S’\) 及び外世界の座標系 \(S\) を表わすミンコフスキー図．光源は系 \(S\) に静止している.発光事象 \(E\) の座標 \((t’_e,z’_e)\) は系 \(S’\) の座標軸への射影により決定される．

光は, 全ての座標系に関して, 4 次元時空内を直線に沿って移動する．従って, ３次元空間座標に制限した場合もそうである．従って, 空間座標 \((x’^{1}_e,y’^{2}_e,z’^{3}_e)\) が, 観測者の基準座標系に於ける入射光の方向を決定し, 観測者が見た光源の見かけの位置を表わしている．
ここで, 入射光の方向は光の相対論的収差によって得られたものと同じである．プレノプティクス関数の変換とは対照的に, 発光事象は深さ情報も提供する．照度の特殊相対論効果は, ドップラー効果とサーチライト効果によって決定される．発光事象の位置変換の後で, それらは入射光のスペクトルパワー分布に適用される．

4.6 外心的な見え方と自心的な見え方の等価性

特殊相対性理論の一つの基本的な特徴は, 全体的な一つの座標系及び全体的な一つの時間は存在しないということである．物理的な世界を記述するのはどの慣性系も等しく正当である．従って, 自心的な見方(egocentric view) すなわち「カメラは静止し物体が動いている」見方と, 外心的な見方(exocentirc view) すなわち「物体は静止しカメラが動いている」見方は,完全に等価である．
それにもかかわらず, ここでは両者の見方が一致することをあえて明示的に示そうと思う．取り上げる問題は, 幾何学的な外観に関することだけとする．ドップラー効果とサーチライト効果は, 通常では一つの方法でしか提示されない．それは外心構造的な見方に等価である．従ってそれらの効果は無視する．(they are usually presented in only one way, equivalent to the exocentric point of view.)
以下の考察は, 観測者の静止系 \(S’\) と物体の静止系 \(S\) の間の関係を基礎としている．一般性を欠くことなく, 映像生成の事象の時に２つの座標系の原点は一致しており, 座標軸は整列しているとしよう．そして, 観測者は系 \(S\) の \(z\)-軸の正方向に沿って速さ \(\beta\) で動いているとしよう．すると, ２つの基準座標系は \(z\)-軸に沿ったローレンツ=ブーストによって相互関係することになる．

図 5. 自心的見方の場合のミンコフスキー図 (a) と, 外心的見方の場合のミンコフスキー図 (b).

4.6.1 入射光の方向

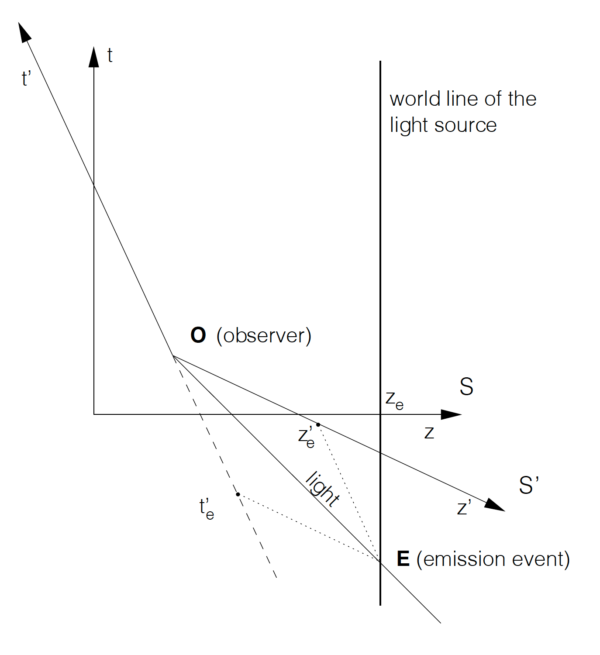
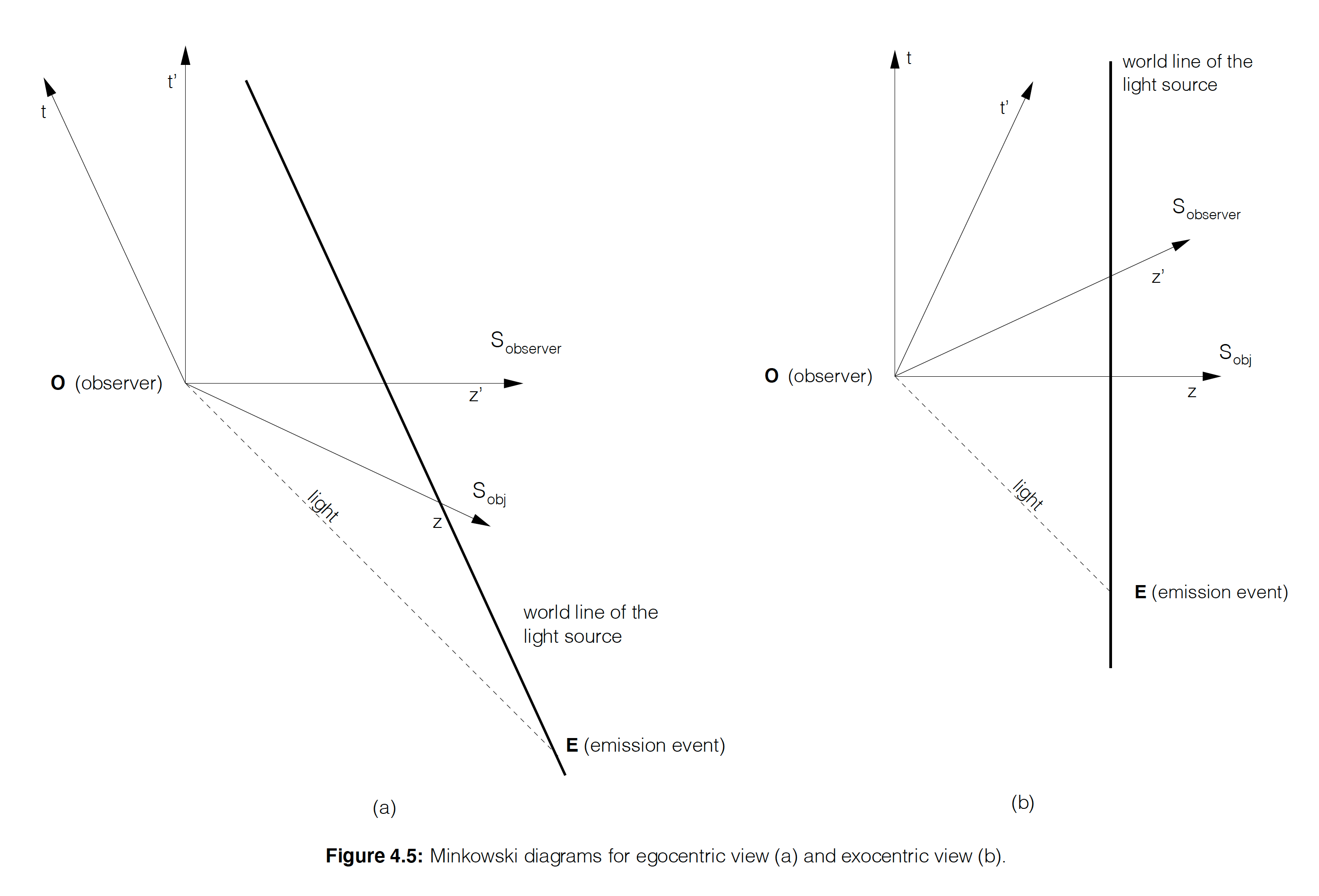
最初に, 入射光の方向は両者の見方で同じであることを示しておく．光は一つの点光源により放射されると考える．図 4.5 は, 各々のミンコフスキー図を示している．
式 (4.31) により, 光源が空間の位置 \((x_E,y_E,z_E)\) の場所にあるならば, 光の放出事象は系 \(S\) で次である：

\begin{equation}
x^{\mu}_E = \left(-\sqrt{x^{2}_E+y^{2}_E+z^{2}_E},\,x_E,\,y_E,\,z_E\right)
\tag{4.32}
\end{equation}

このとき, 成分 \(x^{0}_{E}=-\sqrt{x^{2}_E+y^{2}_E+z^{2}_E}\) は放出事象からカメラでの吸収事象までの飛行時間を表わしている(放出は過去の事象なのでマイナス符号が付いている)．式 (4.31) の代わりに, 放出イベントは球面座標で表現することも出来る．\(r_E=\sqrt{x^{2}_E+y^{2}_E+z^{2}_E}\) とすると,

\begin{equation}
x^{\mu}_E = \big(-r_{E},\,r_{E}\cos\phi_E,\, r_{E}\sin\phi_E\sin\theta_E,\, r_{E}\cos\theta_E\big)
\tag{4.33}
\end{equation}

系 \(S’\) での放出事象\(x’^{\mu}_E\) は, ローレンツ変換によって得られる：

\begin{equation}
x’^{\mu}_E = \Big(-\gamma(r_E+\beta z_E),\,x_E,\,y_E,\,\gamma(z_E+\beta r_E)\Big)
\tag{4.34}
\end{equation}

上式を観測者の基準座標系 \(S’\) に於ける式 (4.33) の類似式と比較することで, 入射光に対応した放出光の方向の角度変換は次のように得られる：

\begin{equation}
\cos\theta’=\frac{\cos\theta-\beta}{1-\beta\cos\theta},\quad \phi’=\phi,
\tag{4.35}
\end{equation}

従って, 光線の方向は外心的な見方と自心的な見方で同じである．外心的な見方は光収差の方程式 (4.19) に基づいている．(Therefore, the direction of the light rays is identical for the egocentric and exocentric point of view, which is based on the aberration equation (4.19).)

4.6.2 可視性

次の関心事は可視性の問題である．ある物体が一つの基準座標で別の物体によって隠れている場合, 他方の全ての座標系でも同様に隠れているであろう．系 \(S\) での可視性を計算し, その結果を \(S’\) で用いることは許されるであろうか？．
全ての系で, 光は４次元時空中を直線に沿って運動する．光線に沿った光の放出事象の次元は, 基準座標を何れに選んでも同じである．従って, 可視性の特性はローレンツ変換によって変化しない．
明示的な計算は以下の通りである．２つの光放出事象 \(E_1\) と \(E_2\) を考えよう．系 \(S\) で, 事象 \(E_2\) は事象 \(E_1\) で隠れているとしよう．各々の座標は, 定数を \(C\gt 1\) として次で関係しているとする：

\begin{equation}
x^{\mu}_{E_2}=Cx^{\mu}_{E_1}
\tag{4.36}
\end{equation}

ローレンツ変換を用いることで, 系 \(S’\) に於ける光放出事象の座標は次となる：

\begin{equation}
x’^{\mu}_{E_2}=Cx’^{\mu}_{E_1}
\tag{4.37}
\end{equation}

光収差の方程式 (4.19) は変換可能であるという事実と結び付けると, ローレンツ変換の下で可視性は不変であることが証明される．逆ローレンツ変換は, 運動方向が逆のローレンツ変換に過ぎないので, 見えないことは系 \(S’\) から系 \(S\) へ変換した場合でもやはり見えないことになる．逆ローレンツ変換は運動方向が逆のローレンツ変換にすぎないので、\(S’\) から \(S\) への変換についても不可視性の不変性が成立する．
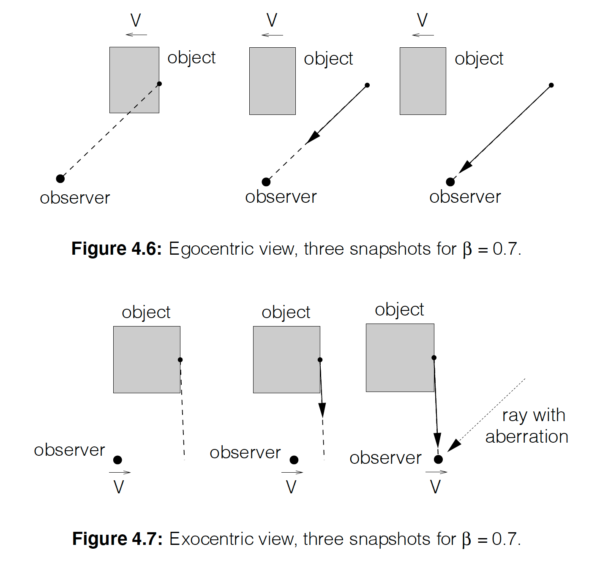
これらの抽象的な計算を全て行った後に於いて,「我々は相対論的な物質の周囲を“見回す”ことが出来, そして後ろ側を見ることが出来る (look “around” and see their back)」ということを, どのようにして説明出来るのであろうか？．図 4.6 と図 4.7 は, 動いている立方体の例での状況を明らかにしたものである．

図 6. 上図は自心的な見方での3枚のスナップショット (\(\beta=0.7\)) である．下図は外心的な見方での3枚のスナップショット (\(\beta=0.7\)) である．

図 4.6 の自心的な見方では, カメラは静止しており, 立方体は \(\beta=0.7\) で左方向に運動している．立方体は運動方向に沿ってローレンツ縮退している．このとき (Here), 立方体はその背面から放射された光線よりも速く動く (outrun) ので, 立方体の背面は見えるようになる．図 4.7 の外心的な見方では, 立方体は静止し, カメラが \(\beta=0.7\) で右方向へ運動している．この場合, 観測者が入射光を記録するとき, 観測者は立方体の後ろに居るので, 立方体の背面は見えるようになる．また, 図 4.7 の最も右側の図は, 自心的な見方と直接比較できるように, 収差に基づく光線の方向を示している．また, 図 4.7 の右端の画像では, 外心的な見方と直接比較できるように, 収差に基づく光線(ray with aberration)の方向を示している．

4.6.3 見かけ上の回転

高速移動する物体の見かけ上の回転は, 前の小節の説明と密接に関係している．自心的な見方で「物体が回転しているように見える」のは, 通常では見えない物体の背面から出た光が物体よりも速く動き, 従ってそれは観察者に届くことが出来るからである．外心構造的な見方では, 観測者はすでに物体の後ろに居り, 従ってその後部を見ることが出来る．しかしながら, 観測者の視点から見ると, 入射光の収差のために, 物体はまだ前方にあるように見える．従って, 物体の裏側を見ることは, 物体の「見かけ上の回転」と解釈されることになる．

4.6.4 まとめ

自心的な見方と外心的な見方は, 特殊相対論的レンダリングに於ける見かけの幾何学的形状については等価であることを示した．両方の見え方を一致させる際の主たる難しさは, 系の全ての物理的構成要素, 特に観察者とオブジェクトの位置を変換することである．
通常, 外心的な見方はより自然な見方と見做され, 従って説明の際のモデルに広く用いられる．実際, 私は以下の理由から, 外心的見方の方がより適切であると考えている．まず, 外心的な見方は, 光の場についての全ての関連情報を一つの操作で変換することを可能とする．第２に, 観測者の加速度運動を, 修正を一切しないで外心的見方に組み入れることが出来る．第３に, 外心的見方は物理的な現実をよりよく反映している．観測者と遠隔物質の間には, 直接的な相互作用は存在しない．周囲の環境の全ての情報は, 光子を通じて観測者に運ばれる．スナップ写真を作成することは, 光子と検出器 (カメラ) の間の局所的な相互作用に基づいている．従って, 観測者に到達する光子を変換することは, カメラから遠く離れた場所で起こった発光イベントを変換することよりもずっと物理的である．

4.7 点粒子の加速

この節では, 特殊相対性理論の中での点粒子の運動学を述べる．加速度を考慮しなければならないのは, 例えば相互作用の技法(interaction technique)や映像物体のアニメーションに於いてである．
粒子の運動学は運動の方程式 (4.15) で記述される：

\begin{equation}
a^{\mu}=\frac{du^{\mu}}{d\tau}=\frac{d^{2}x^{\mu}}{d\tau^{2}}
\tag{4.15′}
\end{equation}

座標系 \(S\) は外部世界の慣性系であり, 座標系 \(S’\) は加速粒子と一緒に動く座標系である．粒子の座標系での加速度が与えられていると仮定しよう．３次元加速度 \((a’_x,a’_y,a’_z)\) から, 座標系 \(S’\) での４-加速度は次のように得られる：

\begin{equation}
a’^{\mu}=\big(0,a’_x,a’_y,a’_z\big)
\tag{4.38}
\end{equation}

４-加速度は, 随伴ローレンツ変換 (associated Lorentz transformation) により系 \(S\) へ変換される．量 \(a^{\mu}\), \(u^{\mu}\), \(x^{\mu}\), そして \(\beta\) は固有時 \(\tau\) の関数である．４-加速度の系 \(S\) へのローレンツ変換は, 時間と空間成分との混合を引き起こし, その結果, 常微分方程式の連成系が生じる．この初期値問題を解くには, よく知られた数値法, 例えば Runge-Kutta 法など,が存在する．最終的に, 粒子の軌跡に沿った４-速度と４-加速度が系 \(S\) について得られる．
重力を無視する限りに於いて, 特殊相対性理論は加速度を完璧に記述することが出来ることに注意して欲しい．(重力は一般相対性理論の領域である)．高エネルギー粒子加速器に於ける粒子の運動学が特殊相対性理論で記述できるという事実は, この主張を裏付ける実験的証拠の一つに過ぎない．例えば, DESY の貯蔵リング HERA (Hadron Electron Ring Accelerator) では, 電子と陽電子は \(30\) GeV のエネルギーまで加速され, およそ \(\beta=0.99999999985\) の速度となる．貯蔵リング内では, これらの粒子は電磁場による加速度で円運動を行う．この加速度の計算及び衝突実験の計算は特殊相対性理論を基礎にしており, それらは実験と完全に一致している．
ローレンツ変換は慣性系のみに限定される．しかしながら, 加速度運動する物体の場合でも時空の各点で一緒に動く慣性系を見出すことが可能である．そのようにして, 慣性系の基準座標から分かっている式を利用することが出来る．一緒に動く基準座標系の概念により, 我々は特殊相対性理論に於いて加速度を取り扱うことが可能となる．図 4.8 は, 短い加速度相の前後での, 粒子と一緒に動く慣性系を図示している．