J.J.Sakurai の第２章に次のような記述がある：
「エネルギー固有状態は \(n\) がどんなに大きくても, \(q\) や \(p\) の期待値が振動している訳ではないので, 古典的振動子のような振舞いをしない．では一体, 古典的振動子と一番よく似たエネルギー固有状態の重ね合わせをどうしたら作れるだろうか？波動関数の言葉で言えば, 形が拡がらずに前後に運動する波束が欲しいのである．非エルミート的な消滅演算子 \(\hat{a}\) の固有値方程式 \(\hat{a}|\lambda\rangle=\lambda |\lambda\rangle\) により定義される「コヒーレント状態」が, この役割りをすることが分かる．
そこで, 枝松圭一著：「単一光子と量子もつれ光子」の第３章から, 引き続き「コヒーレント状態」についての記述を抜粋要約しておくことにする．
\(\)
エネルギー固有状態 (個数状態) に於ける位置と運動量
前のブログ記事で,「個数状態は古典的運動を表わす状態ではない」ことを述べた．このことをもう一度確認しておく．
まず, 「消滅演算子」\(\hat{a}\) と「生成演算子」\(\hat{a}^{\dagger}\) そして「個数演算子」\(\hat{n}\) の定義を確認しておく：
\def\bra#1{\langle #1 |}
\def\ket#1{| #1 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\mb#1{\mathbf{#1}}
\hat{a}\equiv \frac{1}{\sqrt{2}}\bigl(\hat{q}+i\hat{p}\bigr),\quad
\hat{a}\equiv \frac{1}{\sqrt{2}}\bigl(\hat{q}+i\hat{p}\bigr),\quad
\hat{n}\equiv \hat{a}^{\dagger}\hat{a}
\tag{3.19}
\end{equation}
消滅演算子 \(\hat{a}\) と生成演算子 \(\hat{a}^{\dagger}\) の「時間変化」は次である：
\hat{a}(t)=\hat{a}e^{-i\omega t},\quad \hat{a}^{\dagger}(t)=\hat{a}^{\dagger}e^{i\omega t}
\tag{3.46}
\end{equation}
従って, 座標演算子 \(\hat{q}\) と運動量演算子 \(\hat{p}\) の「時間変化」は次となる：
\hat{q}(t)=\frac{1}{\sqrt{2}}\bigl(\hat{a}(t)+\hat{a}^{\dagger}(t)\bigr),\quad
\hat{p}(t)=\frac{1}{i\sqrt{2}}\bigl(\hat{a}(t)-\hat{a}^{\dagger}(t)\bigr)
\tag{3.48}
\end{equation}
このとき \(\BraKet{n}{\hat{a}}{n}=\BraKet{n}{\hat{a}^{\dagger}}{n}=0\) となるので, 個数状態 \(\ket{n}\)に対する「位置及び運動量の期待値は恒常的にゼロとなる」ことが分かる：
\langle q(t)\rangle =\BraKet{n}{\hat{q}(t)}{n}=0,\quad
\langle p(t)\rangle =\BraKet{n}{\hat{p}(t)}{n}=0
\tag{3.49}
\end{equation}
これらの結果は, 明らかに古典的振動運動とは異なっており,「個数状態は古典的振動運動に対応した量子状態とはなっていない」ことが分かる．これはしかし,「位置や運動量が常にゼロに固定されていることを意味するものではない」．実際, 一般化座標に変換する前の「観測量である位置演算子」\(x(t)\) と「観測量である運動量演算子」 \(p(t)\) に対する「ハイゼンベルグの運動方程式」を用いて, それらの時間発展を具体的に求めてみると次となる：
x(t)=q(0)\cos\omega t +\frac{p(0)}{m\omega}\sin \omega t,\quad
p(t)=-m\omega x(0)\sin\omega t +p(0)\cos\omega t
\end{equation*}
これらは, 古典的な運動方程式と同じに見える．「この \(x\)-演算子と \(p\)-演算子は, 古典論の場合と同じように ”振動している” のである!」．そこで, この位置座標 \(x\) とその運動量 \(p\) の「ゆらぎ」(不確定性) を求めてみると,
\begin{align*}
&\langle \hat{x}(t)\rangle=\BraKet{n}{\hat{x}(t)}{n}=0,\quad
\langle \hat{p}(t)\rangle=\BraKet{n}{\hat{p}(t)}{n}=0,\\
&\langle \hat{x}(t)^{2}\rangle =\BraKet{n}{\hat{x}(t)^{2}}{n}=
\frac{\hbar}{m\omega}\left(n+\frac{1}{2}\right),\quad
\langle \hat{p}(t)^{2}\rangle =\BraKet{n}{\hat{p}(t)^{2}}{n}=m\hbar\omega\left(n+\frac{1}{2}\right)
\end{align*}
従って,
\begin{align*}
&\sigma(q)^{2}=\langle \hat{q}(t)^{2}\rangle -\langle \hat{q}(t)\rangle^{2}=
\left(n+\frac{1}{2}\right),\notag\\
&\sigma(p)^{2}=\langle \hat{p}(t)^{2}\rangle -\langle \hat{p}(t)\rangle^{2}
=\left(n+\frac{1}{2}\right)
\tag{3.53}
\end{align*}
となり, \(n\) に応じて一定のゆらぎを持つ．すなわち「個数状態に於いては, １次元調和振動子系は定まった位相を持たない乱雑な振動をしており, \(q\) や \(p\) の平均値はゼロであるが, 有限のゆらぎを持つ」のである．特に, \(n=0\) に於いても有限のゆらぎを持ち, これを「零点ゆらぎ」または「零点振動」とも言う．
コヒーレント状態
以上のことを逆に言うならば,「古典的運動を表わすような量子状態があるとすれば, それは２つ以上の個数状態の何らかの線形結合 (重ね合わせ) となっているはず」である．そこで, 古典的振動状態に対応した量子状態として, グラウバー(G.Glauber) によって考案された「コヒーレント状態」( coherent state ) を導入しょう．
「コヒーレント状態 \(\ket{\alpha}\) は, 消滅演算子 \(\hat{a}\) の固有状態として定義される」：
\[ \hat{a}\ket{\alpha}=\alpha\ket{\alpha},\quad\hat{a}\equiv \frac{1}{\sqrt{2}}\bigl(\hat{q}+i\hat{p}\bigr),\ \,
\hat{a}^{\dagger}\equiv \frac{1}{\sqrt{2}}\bigl(\hat{q}-i\hat{p}\bigr)\tag{3.94}\]
ここで \(\alpha\) は一般に複素数の固有値である．また \(\ket{\alpha}\) は規格化されている．また, コヒーレント状態に対する消滅演算子 \(\hat{a}\) と生成演算子 \(\hat{a}^{\dagger}\) 及び個数演算子 \(\hat{n}=\hat{a}^{\dagger}\hat{a}\) の期待値は次である：
\BK{\alpha}{\alpha}=1,\quad
\BraKet{\alpha}{\hat{a}}{\alpha}=\alpha,\quad
\BraKet{\alpha}{\hat{a}^{\dagger}}{\alpha}=\alpha^{\dagger},\quad
\BraKet{\alpha}{\hat{n}}{\alpha}=|\alpha|^{2}
\tag{3.98}
\end{equation}
上式などから, コヒーレント状態に対する \(q\) と \(p\) の期待値は次となる：
\BraKet{\alpha}{\hat{q}(t)}{\alpha}&=\frac{1}{\sqrt{2}}\bigl(\alpha e^{-i\omega t}+
\alpha^{\dagger} e^{i\omega t}\bigr)=\sqrt{2}\,\mathrm{Re}\bigl(\alpha e^{-i\omega t}\bigr)\tag{3.99}\\
\BraKet{\alpha}{\hat{p}(t)}{\alpha}&=\frac{1}{i\sqrt{2}}\bigl(\alpha e^{-i\omega t}-
\alpha^{\dagger} e^{i\omega t}\bigr)=\sqrt{2}\,\mathrm{Im}\bigl(\alpha e^{-i\omega t}\bigr)\tag{3.100}
\end{align}
すなわち「\(q\) および \(p\) の期待値は, 振幅 \(\sqrt{2}\alpha\) で時間的に振動し, 位相空間上で円運動を行う」ことが分かる．これらは \(Q=\sqrt{\hbar}\,q\) 及び \(P=\sqrt{\hbar}\,p\) の古典的運動と対応している．また, そのときの \(q\) 及び \(p\) の「ゆらぎ」(不確定性) は,
&\sigma_\alpha (q)^{2}=\BraKet{\alpha}{\hat{q}(t)^{2}}{\alpha}
-\BraKet{\alpha}{\hat{q}(t)}{\alpha}^{2}=\frac{1}{2},\tag{3.101}\\
&\sigma_\alpha (p)^{2}=\BraKet{\alpha}{\hat{p}(t)^{2}}{\alpha}
-\BraKet{\alpha}{\hat{p}(t)}{\alpha}^{2}=\frac{1}{2}\tag{3.102}
\end{align}
となり, 振幅や時間に依らず一定のゆらぎを持つ．コヒーレント状態に於ける位置および運動量の「ゆらぎ」は, 真空状態 \(\ket{0}\) に於けるそれと同じ量となり, 最小の不確定性関係にあることが分かる．すなわち「コヒーレント状態とは, 古典的振動状態に対応した量子状態であって, \(\sqrt{2}\,\alpha\) は \(q\), \(p\) の複素振幅に対応し, それらの「ゆらぎ」は最小不確定性関係にある」．
このコヒーレント状態 \(\ket{\alpha}\) を個数状態 \(\ket{n}\) の線形結合で表しておこう．
\ket{\alpha}=\sum_n c_n\,\ket{n},\quad c_n = \BK{n}{\alpha}=\frac{\alpha^{n}}{\sqrt{n!}}\BK{0}{\alpha}
\tag{3.104}
\end{equation}
ここで \(c_0=\BK{0}{\alpha}\) を実数にとるならば \(\sum_n|c_n|^{2}=1\) より \(c_0=e^{-|\alpha|^{2}/2}\) となるので結局次を得る：
\ket{\alpha}=e^{-\frac{|\alpha|^{2}}{2}}\sum_n \frac{\alpha^{n}}{\sqrt{n!}}\ket{n}
\tag{3.107}
\end{equation}
このときの係数 \(c_n\) については,
|c_n|^{2}=\frac{|\alpha|^{2n}}{n!}\,e^{-|\alpha|^{2}}
\tag{3.108}
\end{equation}
となり, これは平均値 \(|\alpha|^{2}\) のポアソン分布を表している．すなわち「コヒーレント状態を個数状態 \(\ket{n}\) に見出す確率はポアソン分布になる」ことが分かる．
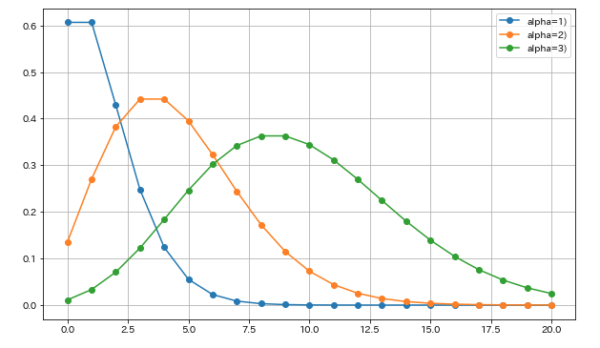
図 1. コヒーレント状態\(\ket{\alpha}\) を個数状態 \(\ket{n}\) に見出す確率はポアソン分布となる．
さらにコヒーレント状態 \(\ket{\alpha}\) は, 個数状態が \(\ket{n}=\frac{1}{\sqrt{n!}}\big(\hat{a}^{\dagger}\big)^{n}\ket{0}\) と表せることから, 次のように表わすことも出来る：
\ket{\alpha}&= e^{-\frac{|\alpha|^{2}}{2}}\sum_n \frac{\alpha^{n}}{\sqrt{n!}}
\left(\frac{1}{\sqrt{n!}}\big(\hat{a}^{\dagger}\big)^{n}\ket{0}\right)
=e^{-\frac{|\alpha|^{2}}{2}}\sum_n \frac{\big(\alpha\hat{a}^{\dagger}\big)^{n}}{n!}\ket{0}\notag\\
&=e^{-\frac{|\alpha|^{2}}{2}}\,e^{\alpha \hat{a}^{\dagger}}\ket{0}
=e^{-\frac{|\alpha|^{2}}{2}}\,e^{\alpha \hat{a}^{\dagger}}e^{-\alpha^{*}\hat{a}}\ket{0}
\tag{3.111}
\end{align}
ただし最後の式では, 消滅演算子について \(\hat{a}\ket{0}=0\) が言えるので, 次式が成り立つことを利用している：
e^{-\alpha^{*}\hat{a}}\ket{0}=\left(\sum_{n}\frac{\bigl(-\alpha^{*}\hat{a}\bigr)^{n}}{n!}\right)\ket{0}
=\left(1+\frac{-\alpha^{*}\hat{a}}{1!}+\frac{(-\alpha^{*}\hat{a})^{2}}{2!}+\dotsb\right)\ket{0}
=\ket{0}
\end{equation*}
さらに, 次の「Baker-Campbell-Hausdorff の定理」
２つの演算子 \(\mb{A}\) と \(\mb{B}\) の交換子を \(\mb{C}=[\mb{A},\mb{B}]\) としたときに, \(\mb{C}\) が \(\mb{A}\), \(\mb{B}\) の両方と交換可能, すなわち \([\mb{C},\mb{A}]=[\mb{C},\mb{B}]=0\) ならば,
\begin{equation*}
\exp\bigl(\mb{A}+\mb{B}\bigr)=\exp\bigl(\mb{A}\bigr)\exp\bigl(\mb{B}\bigr)
\exp\left(-\frac{1}{2}\mb{C}\right)
\end{equation*}
が成り立つ．
を利用する． 消滅演算子 \(\hat{a}\) と生成演算子 \(\hat{a}^{\dagger}\) についての交換関係は
[\hat{a},\hat{a}^{\dagger}]=1,\quad\rightarrow\quad [\hat{a}^{\dagger},\hat{a}]=-1
\end{equation*}
なので \(\mb{A}=\alpha\hat{a}^{\dagger}, \mb{B}=-\alpha^{*}\hat{a}\) とすると
\mb{C}=[\alpha\hat{a}^{\dagger},-\alpha^{*}\hat{a}]=-\alpha\alpha^{*}[\hat{a}^{\dagger},\hat{a}]
=|\alpha|^{2}\quad\rightarrow\quad \exp\left(-\frac{1}{2}\mb{C}\right)
=\exp\left(-\frac{1}{2}|\alpha|^{2}\right)
\end{equation*}
となる．従って,「Baker-Campbell-Hausdorff の定理」から, コヒーレント状態は次のようにも表わせる：
&\ket{\alpha}=e^{\alpha \hat{a}^{\dagger}}e^{-\alpha^{*}\hat{a}}e^{-\frac{|\alpha|^{2}}{2}}\,\ket{0}
=e^{\alpha \hat{a}^{\dagger}-\alpha^{*}\hat{a}}\,\ket{0}
\equiv \hat{S}(\alpha)\ket{0},\tag{3.113}\\
&\psi_{\alpha}(q)=\BK{q}{\alpha}=\BraKet{q}{\hat{S}(\alpha)}{0}\notag
\end{align}
このときの演算子 \(\hat{S}(\alpha)\equiv e^{\alpha \hat{a}^{\dagger}-\alpha^{*}\hat{a}}\) を「変位演算子」( displacement operator ) と言う．
座標表示での \(\hat{S}(\alpha)\) の効果を調べてみよう．\(\sqrt{2}\,\alpha=\xi+i\eta\) と置く．すなわち \(\xi=\sqrt{2}\,\mathrm{Re}\ \alpha\), \(\eta=\sqrt{2}\,\mathrm{Im}\ \alpha\) である．すると \(\hat{a}=\frac{1}{\sqrt{2}}(\hat{q}+i\hat{p})\)，\(\hat{a}^{\dagger}=\frac{1}{\sqrt{2}}(\hat{q}-i\hat{p})\) であるから,
\begin{align*}
\alpha \hat{a}^{\dagger}-\alpha^{*}\hat{a}
&=\frac{1}{\sqrt{2}}(\xi+i\eta)\frac{1}{\sqrt{2}}(\hat{q}-i\hat{p})
-\frac{1}{\sqrt{2}}(\xi-i\eta)\frac{1}{\sqrt{2}}(\hat{q}+i\hat{p})\\
&=i\eta\hat{q}-i\xi\hat{p}
\end{align*}
よって交換関係 \([\hat{q},\hat{p}]=i\) を用いると \([i\eta \hat{q},-i\xi \hat{p}]=\eta\xi[\hat{q},\hat{p}]=i\eta\xi\) が言える．そこで「Baker-Campbell-Hausdorff の定理」を利用すると, \(\hat{S}(\alpha)\) は次式のように表わせる：
\hat{S}(\alpha)=e^{\alpha \hat{a}^{\dagger}-\alpha^{*}\hat{a}}
=e^{i\eta\hat{q}-i\xi\hat{p}}=e^{i\eta\hat{q}}\,e^{-i\xi\hat{p}}e^{-i\frac{1}{2}\eta\xi}
=e^{i\eta\hat{q}}\,\mathscr{T}_q(\xi)e^{-i\frac{1}{2}\eta\xi}
\tag{3.114}
\end{equation}
この結果式の第２因子は「平行移動演算子」\(\mathscr{T}(\xi)\) と見做すことが出来るので, 関数 \(\psi_{\alpha}(q)\) は次のように書くことが出来る：
\begin{align*}
\psi_{\alpha}(q)&=\BK{q}{\alpha}=\BraKet{q}{\hat{S}(\alpha)}{0}
=e^{i\eta q}e^{-i\frac{1}{2}\eta\xi}\BraKet{q}{\mathscr{T}(\xi)}{0}\\
&=e^{i\eta q}e^{-i\frac{1}{2}\eta\xi}\BK{q-\xi}{0}
=e^{i\eta q}e^{-i\frac{1}{2}\eta\xi}\psi_{0}(q-\xi),\\
\rightarrow\ \psi_{\alpha}\left(q+\frac{\tau}{2}\right)
&=e^{i\eta\left(q+\frac{\tau}{2}\right)}e^{-i\frac{1}{2}\eta\xi}\psi_{0}
\left(q+\frac{\tau}{2}-\xi\right),\\
\psi^{*}_{\alpha}\left(q-\frac{\tau}{2}\right)
&=e^{-i\eta\left(q-\frac{\tau}{2}\right)}e^{i\frac{1}{2}\eta\xi}\psi^{*}_{0}
\left(q-\frac{\tau}{2}-\xi\right)
\end{align*}
従って, ウィグナー関数は次となる：
W_{\alpha}(q,p)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}d\tau\,e^{-ip\tau}
\psi_{\alpha}\left(q+\frac{\tau}{2}\right)\psi_{\alpha}^{*}\left(q-\frac{\tau}{2}\right)\notag\\
=\frac{1}{2\pi}&\int_{-\infty}^{\infty}d\tau\,e^{-ip\tau}
e^{i\eta\left(q+\frac{\tau}{2}\right)}e^{-i\frac{1}{2}\eta\xi}
\psi_{0}\left(q+\frac{\tau}{2}-\xi\right)e^{-i\eta\left(q-\frac{\tau}{2}\right)}e^{i\frac{1}{2}\eta\xi}
\psi^{*}_{0}\left(q-\frac{\tau}{2}-\xi\right)\notag\\
=\frac{1}{2\pi}&\int_{-\infty}^{\infty}d\tau\,e^{-i(p-\eta)\tau}\,
\psi_{0}\left(q-\xi+\frac{\tau}{2}\right)\psi^{*}_{0}\left(q-\xi-\frac{\tau}{2}\right)\notag\\
\!\!\!\!=W_0&\big(q-\xi,p-\eta\big)=\frac{1}{\pi}e^{-(q-\xi)^{2}-(p-\eta)^{2}}
\tag{3.116}
\end{align}
よって, 変位演算子 \(\hat{S}(\alpha)\) の効果は「位相空間 \((q,p)\) に於いて, ウィグナー関数 \(W_0(q,p)\) を, 複素振幅 \(\sqrt{2}\,\alpha=\sqrt{2}(\mathrm{Re}\,\alpha,\mathrm{Im}\,\alpha)\) だけ平行移動すること」に相当すると言える．真空状態に相当するウィグナー関数 \(W_0(q,p)\) は, 式 (3.93) で与えたように原点を中心としたガウス型であるから, コヒーレント状態のウィグナー関数 \(W_{\alpha}(q,p)\) は, 複素振幅 \(\sqrt{2}\,\alpha\) を中心としたガウス型となる．
また, \(\ket{\alpha}\) の時間発展は次となる：
e^{-i\hat{H}t/\hbar}\ket{\alpha}&=e^{-\frac{|\alpha|^{2}}{2}}\sum_n \frac{\alpha^{n}}{\sqrt{n!}}
e^{-i\left(n+\frac{1}{2}\right)\omega t}\ket{n}
=e^{-i\frac{1}{2}\omega t}\,e^{-\frac{|\alpha|^{2}}{2}}\sum_n
\frac{(\alpha\,e^{-i\omega t})^{n}}{\sqrt{n!}}\ket{n}\notag\\
&=e^{-i\frac{1}{2}\omega t}\,\ket{\alpha\,e^{-i\omega t}}
\tag{3.117}
\end{align}
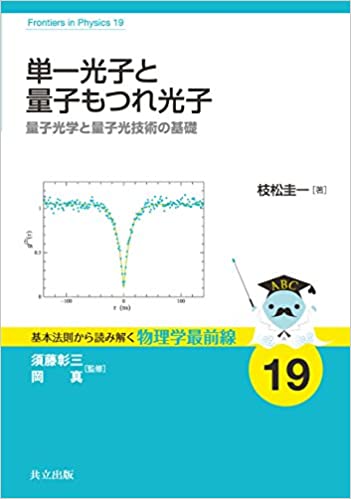
よって, そのウィグナー関数の中心は, 複素振幅 \(\sqrt{2}\,\alpha\,e^{-i\omega t}\) にあり, 位相空間上を角速度 \(\omega\) で時計回り回転する．その結果, 下図に示すように \(q\) の確率密度およびその期待値 (3.99) は時間と共に振動する．
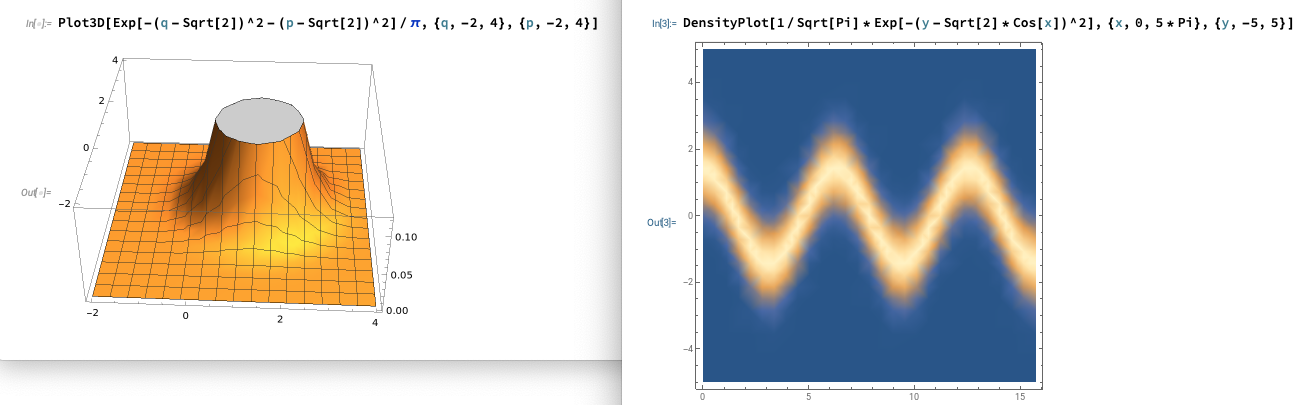
図 2. コヒーレント状態 \(\ket{\alpha} (\alpha=\sqrt{2})\) のウィグナー関数, およびその確率密度 \(|\psi_{\alpha}(q)|^{2}\) の時間変化(横軸は \(\omega t\) である)．
この \(q\) は「古典電磁気学の電場 \(\mb{E}\) または磁場 \(\mb{H}\)」を一般化座標に変換したものと考えるならば,「この図は一様な媒質中を進む光が作る電磁場(平面波) の振動状態を表している」と言えるであろう．以下は§ 4.1「電磁場の量子化」からの抜粋である：
電場の実部 \(E_r\)と虚部 \(E_i\) に対応するエルミート演算子を
\hat{E}_r = \sqrt{\frac{\omega}{\epsilon V}}\,\hat{Q}
=\sqrt{\frac{\hbar\omega}{\epsilon V}}\,\hat{q},\qquad
\hat{E}_i = \sqrt{\frac{\omega}{\epsilon V}}\,\hat{P}
=\sqrt{\frac{\hbar\omega}{\epsilon V}}\,\hat{p}\tag{4.15}
\end{equation}
と定義する．これらの演算子の時間変化は次となる：
\hat{E}_r &=\sqrt{\frac{\hbar\omega}{\epsilon V}}\,\hat{q}
=\sqrt{\frac{\hbar\omega}{2\epsilon V}}\bigl(\hat{a}\,e^{-i\omega t}
+\hat{a}^{\dagger}\,e^{i\omega t}\bigr)\tag{4.16}\\
\hat{E}_i &=\sqrt{\frac{\hbar\omega}{\epsilon V}}\,\hat{p}
=\frac{1}{i}\sqrt{\frac{\hbar\omega}{2\epsilon V}}\bigl(\hat{a}\,e^{-i\omega t}
-\hat{a}^{\dagger}\,e^{i\omega t}\bigr)
\tag{4.17}
\end{align}
すなわち, 電場の実部および虚部の演算子は \(\hat{q}\) 及び \(\hat{p}\) に比例しており,「電場に関する種々の物理量を求めることは, \(\hat{q}\) および \(\hat{p}\) に関するそれらを求めることと同等である」．
