Feynmann QED の第2章は特殊相対論の要約になっている．座標系をローレンツ変換すると, 時間と普通の座標とが互いに混ざり合うことになる．そのため相対論では, 普通の 3次元の空間に時間の軸を加えた 4次元の空間を考え, その中の一種の回転によって ４つの座標が 1次変換を受けると考える．このような 4次元の空間のことを「Minkowski 空間」, または「Minkowski 時空」と呼んでいる．この 4次元時空を表現する主な方法には ２つある．一つは「虚時間座標」 \(x_4=ict\) を用いる方法, もう一つは「実数の時間座標 」 \(x_0=ct\) を用いるものである．またミンコフスキー計量も \(\eta^{\,\mu\nu}=(-1,1,1,1)\) とするか \(\eta^{\,\mu\nu}=(1,-1,-1,-1)\) とするかの 2通りがある．従って, 相対論的数式の表現が論文や教科書によってまちまちであって, 初心者が文献を参照するのは非常に大変である．そこで, 主に W.パウリ：「相対性理論」の§7, §24 の文章を抜粋して, 4元量の表現方法とその座標表現を簡単にまとめておこう．
\(\)
§ 7 4次元世界(Minkowski)
相対性の要請と光速度不変の要請は,「すべての物理法則がローレンツ群に対して不変でなければならない」という一つの要請にまとめられる．今後は「ローレンツ群」というときは次の恒等式
\begin{equation}
s’^{2}=(x’)^{2}+(x’)^{2}+(x’)^{2}-(ct’)^{2}=x^{2}+y^{2}+z^{2}-(ct)^{2}=s^{2}
\tag{II}
\end{equation}
s’^{2}=(x’)^{2}+(x’)^{2}+(x’)^{2}-(ct’)^{2}=x^{2}+y^{2}+z^{2}-(ct)^{2}=s^{2}
\tag{II}
\end{equation}
を満足するすべての一次変換(これは \(\infty^{10}\) 個ある．つまり \(10\) 個のパラメーターに依存する変換である)の全体をさすものとする．この群に属する任意の変換は3次元空間座標軸の回転(これに鏡像変換も含めてよろしい)と, 次の特殊ローレンツ変換
\begin{equation*}
x’=\frac{x-vt}{\sqrt{1-\beta^{2}}},\quad y’=y,\quad z’=z,\quad t’=\frac{t-(v/c^{2})x}{\sqrt{1-\beta^{2}}}
\tag{I}
\end{equation*}
x’=\frac{x-vt}{\sqrt{1-\beta^{2}}},\quad y’=y,\quad z’=z,\quad t’=\frac{t-(v/c^{2})x}{\sqrt{1-\beta^{2}}}
\tag{I}
\end{equation*}
との組み合わせで作ることができる．数学的にいえば, 特殊相対性理論とはローレンツ群に対する不変論にほかならない．相対性理論の発展にとって Minkowski の研究はきわめて重要な基本的な役割を演じた．彼は次の二つの事実に着目することによって, 理論をきわめて見透しのよい形式に書きあらわした:
- もし普通の時間座標 \(t\) の代わりに虚数 \(u=ict\) を用いるならば, ロー レンツ群に対して, またこの群に対して不変な物理法則に関して, 空間座標変数 \(x,y,z\) と虚時間座標 \(u\) の間には形式的に何等の差違も存在せず, これら4個の変数はまったく同等である．実際ローレンツ変換にとって特徴的な不変量
\begin{equation*}
s^{2}=x^{2}+y^{2}+z^{2}-(ct)^{2}
\end{equation*}
は \(u\) を使うことで,
\begin{equation}
s^{2}=x^{2}+y^{2}+z^{2}+u^{2}
\tag{18}
\end{equation}
となる．従って最初から空間と時間を分離せず, これらを一緒にして「時空」と呼ばれる4次元多様体として扱う方が便利である．今後はこのように融合的に考えた「時空」という多様体を Minkowski に従って「世界」と呼ぶことにする． - 式 (18) はローレンツ変換に対して不変であり, それは時空内の点の座標の 2次形式である．そこで, 3次元ユークリッド空間における距離の 2乗が \(x^2+y^2+z^2\) で与えられることに真似て「世界点\(P\) (その座標が \(x, y, z, u\)) と座標原点 \(O\) 間の距離の 2乗は式 (18) で与えられる」とする．この「4次元的距離」の定義は極めて妥当なものと言えよう [1][ブログ註] 式 \((II)\) の不変量 \(s^2\) は, 事象の起った点 \(x_i\) と原点 \(O\) の「4元的距離の2乗」と呼ばれる．．この定義を与えることにより「世界幾何学(計量)」は規定される．それは 4次元ユークリッド幾何学と非常によく似たものである」．しかし両者は完全に同じとは言えない．なぜなら「\(u\) は純虚数である」からである．例えば 2個の世界点の間の距離がゼロでも \(u\) が虚数であるために, これらの世界点が同一の点とは限らない．このような幾何学的性質のちがいが存在するにもかかわらず, 我々はローレンツ変換を「世界座標の一次直交変換」と見做すことが出来る．すなわち 3次元ユークリッド空間 \(R_3\) に於ける座標系の回転に倣って, 「ローレンツ変換を 4次元世界座標軸の”(虚の)回転”と見做す」ことが出来る．さらに 3次元ユークリッド空間に於ける普通のベクトル解析やテンソル解析は \(R_{3}\) に於ける座標系の一次直交変換に対する不変論であると考えられるように, ローレンツ群に対する不変論は「4次元的ベクトル解析」や「4次元的テンソル解析」の形で書き表わされる [2][ブログ註] (ランダウ：「場の古典論」§2 を参考) 一定の速度で相対運動している基準系 \(K\) を考える．\(K\) 系での座標が \((x_1,y_1,z_1)\) … Continue reading．いままで述べたことをまとめると, 相対性理論を Minkowski の考えに従って表現するために重要な上述の第2 の観点を,次のように言い表わすことが出来よう:
口ーレンツ変換は 4次元世界座標の 2次形式を不変に保つ．従って, 口ーレンツ群に対する不変論は幾何学的に表現され得る．それは普通の 3次元的ベクトル・テンソル解析を 4次元多様体の場合へー般化したものとして書き表わされる．
§ 24 口ーレンツ変換の4次元的表現.
相対論的運動学に関する結果は,「4次元時空」という立場に立つともっと見透しのよい形に表現される．その場合, 2つの異なる表現法がある．
一つは「虚時間座標」を用いるもので \(x^{k}\) として
\begin{equation}
x^{1}=x,\quad x^{2}=y,\quad x^{3}=z,\quad x^{4}=ict
\end{equation}
x^{1}=x,\quad x^{2}=y,\quad x^{3}=z,\quad x^{4}=ict
\end{equation}
とする方法である．この方法は歴史的には古く, すでに Poincaré により提唱された．この方法を用いると, 特殊ローレンツ変換 \((I)\) は次のようになる:
\begin{equation}
\begin{cases}
x’^{1}=x^{1}\cos\phi + x^{4}\sin\phi\\
x’^{4}=-x^{1}\sin\phi +x^{4}\cos\phi
\end{cases}
\tag{186-a}
\end{equation}
\begin{cases}
x’^{1}=x^{1}\cos\phi + x^{4}\sin\phi\\
x’^{4}=-x^{1}\sin\phi +x^{4}\cos\phi
\end{cases}
\tag{186-a}
\end{equation}
ただし \(\phi\) は「虚数の角度」で \(\phi=i\psi\) である．この変換式の形は３次元ユークリッド空間 \(R_3\) に於ける座標軸の回転に対する公式と非常によく似ている．この公式が初めて姿を見せたのは Minkowski の論文 II [3]\(\mathit{Math.}\ \) \(\mathit{Ann.},\ \) \(\mathbf{68}\ \) (1910)\(\ \) 526 である．Minkowski の論文では \(\phi\) の代わりに角が虚数であることがはっきり分かるように \(i\psi\) と書いてある．\(x’^{1}=0\) とすれば \(x=vt\) となるはずだから \(\phi\) は \(\tan\phi=i\beta\) で与えられる [4][ブログ註] 式 \((I)\) で \(x’=0\) とおくと \(x-vt=0\) より \(x/t=v\) である．また, 式 (186-a) で \(x’^{1}=0\) … Continue reading この結果と式 \((I)\) と式 (24.2) の比較から, 次の関係が成り立つ：
\begin{equation}
\cos\phi=\frac{1}{\sqrt{1-\beta^{2}}}\equiv \gamma, \quad
\sin\phi=\frac{i\beta}{\sqrt{1-\beta^{2}}}=i\beta\gamma, \quad \tan\phi=i\beta
\tag{187-a}
\end{equation}
\cos\phi=\frac{1}{\sqrt{1-\beta^{2}}}\equiv \gamma, \quad
\sin\phi=\frac{i\beta}{\sqrt{1-\beta^{2}}}=i\beta\gamma, \quad \tan\phi=i\beta
\tag{187-a}
\end{equation}
「虚時間座標 \(x’^{4}=ict\) を用いれば特殊ローレンツ変換は「回転」にほかならない．ただしその「回転角 \(\phi\) は虚数である」．次の 図1 の右側の部分はローレンツ収縮を示したものである．この図では, 横軸は \(x^{1}=x\) を, 縦軸は \(x^{4}=ict\) を表わす．ただし図では, あたかも実数のように描かれている．
第 3 図
\(K’\) 系に静止している棒の両端の世界線は図では \(L_1,L_2\) により表されている．これらの間の距離 \(l_0\) が棒の“静止のときの長さ”である．この棒を \(K\) から眺めれば棒は速さ \(v\) で運動している．\(K\) からみた棒の長さ \(l\) は点 \(P,Q\) の間の距離に等しい．\(l\) と \(l_0\) の間には， 図から明らかなように
\begin{equation}
l=\frac{l_0}{\cos\phi}
\tag{188}
\end{equation}
l=\frac{l_0}{\cos\phi}
\tag{188}
\end{equation}
という関係がなりたつ．この式に式 (24.3) を代入すれば
\begin{equation}
l=\frac{l_0}{\cos\phi},\quad \cos\phi=\frac{1}{\sqrt{1-\beta^{2}}}\quad\rightarrow\quad l=l_0\sqrt{1-\beta^{2}}
\end{equation}
l=\frac{l_0}{\cos\phi},\quad \cos\phi=\frac{1}{\sqrt{1-\beta^{2}}}\quad\rightarrow\quad l=l_0\sqrt{1-\beta^{2}}
\end{equation}
となり,「ローレンツ収縮」の式となる．まったく同様に Einstein の言う「時計の遅れ」も図の左の部分から明らかである．一般に任意の周期的現象は時計として利用できる．そこで, そのような時計が \(K’\) 系に静置されているとする．周期的に起る現象の世界点は \(x’^{4}\) 軸に平行な 1本の直線の上に等間隔に並ぶ．これらの世界点の隣り同士の間隔を \(K’\) からみたとき \(\tau\) とする．これがこの現象の普通にいう“周期”である (簡単のために光速度 \(c\) が \(1\) となるように時間単位が決められているものとする)．この周期現象を \(K\) から眺めたとき, その周期はこれら各々の世界点を \(x^{4}\) 軸上に射影 (\(x^{1}\) 軸に平行に射影) することにより求められる．すなわち \(K\) から見た周期 \(t\) は図からすぐ分かるように
\begin{equation}
\frac{t}{\tau}=\cos\phi\quad\rightarrow\quad \tau=\frac{t}{\cos\phi}
\tag{189}
\end{equation}
\frac{t}{\tau}=\cos\phi\quad\rightarrow\quad \tau=\frac{t}{\cos\phi}
\tag{189}
\end{equation}
この結果に式 (187-a) を用いれば,
\begin{equation}
\tau=t\sqrt{1-\beta^{2}}
\end{equation}
\tau=t\sqrt{1-\beta^{2}}
\end{equation}
となり,「\(K\) に静止している時計 \(U\) の刻む時間のスケールで測ると \(K\) に対して速さ \(v\) で走っている時計 \(U’\) の読み \(\tau\) は \(U\) の読み \(t\) に比べて \(\sqrt{1-\beta^{2}}:1\) の割合で遅れる」ことが示される．この \(\tau\) はこの時計の「固有時間」にほかならない．すなわち \(\tau\) は, この時計 \(U’\) に密着して一緒に運動している観測者により測定された時間である．
もう一つの方法は「実数の時間」を用いて
\begin{equation}
x^{1}=x,\quad x^{2}=y,\quad x^{3}=z,\quad x^{4}=ct
\end{equation}
x^{1}=x,\quad x^{2}=y,\quad x^{3}=z,\quad x^{4}=ct
\end{equation}
とするものである．この第2 の方法は Minkowski が彼の講演：“空間と時間” に於いて初めて採用したものである．この場合の特殊ローレンツ変換 \((I)\) は次となる:
\begin{equation}
\begin{cases}
x’^{1}=x^{1}\cosh\psi\ -\ x^{4}\sinh\psi\\
x’^{4}=-x^{1}\sinh\psi\ +\ x^{4}\cosh\psi
\end{cases}
\tag{186-b}
\end{equation}
\begin{cases}
x’^{1}=x^{1}\cosh\psi\ -\ x^{4}\sinh\psi\\
x’^{4}=-x^{1}\sinh\psi\ +\ x^{4}\cosh\psi
\end{cases}
\tag{186-b}
\end{equation}
このとき \(\psi\) は \(\tanh\psi=\beta\) で与えられ次の関係が成り立つ：
\begin{equation}
\cosh\psi=\frac{1}{\sqrt{1-\beta^{2}}}=\gamma,\quad
\sinh\psi=\frac{\beta}{\sqrt{1-\beta^{2}}}=\beta\gamma,\quad \tanh\psi=\beta
\tag{187-b}
\end{equation}
\cosh\psi=\frac{1}{\sqrt{1-\beta^{2}}}=\gamma,\quad
\sinh\psi=\frac{\beta}{\sqrt{1-\beta^{2}}}=\beta\gamma,\quad \tanh\psi=\beta
\tag{187-b}
\end{equation}
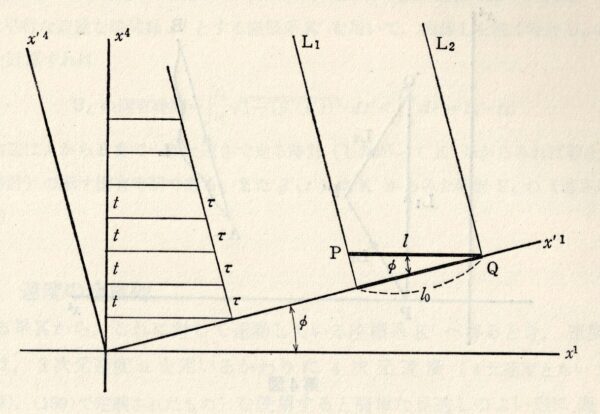
Minkowski 空間をローレンツ変換すると斜交座標となる
次に式 (186-b) のローレンツ変換に於いて新しい座標系は「斜交座標」で表せることを説明する [5][ブログ註] Minkowski 空間自身は, 完全なユークリッド空間ではないので「擬ユークリッド空間」と呼ばれるが, 斜交系ではないので注意する．．まず \(x^{1}\) 軸の変換を考える．\(x’^{1}\) 軸は \(x’^{4}=0\) と表せる．これを式 (186-b) の第 ２ 式に代入すると,
\begin{equation}
-x^{1}\sinh\psi +x^{4}\cosh\psi=0\quad\rightarrow\quad
x^{4}=\frac{\sinh\psi}{\cosh\psi}x^{1}=\tanh\psi\ x^{1}
\end{equation}
-x^{1}\sinh\psi +x^{4}\cosh\psi=0\quad\rightarrow\quad
x^{4}=\frac{\sinh\psi}{\cosh\psi}x^{1}=\tanh\psi\ x^{1}
\end{equation}
これは傾き \(\tanh\psi\) の原点を通る直線である．同様に \(x’^{4}\) 軸は \(x’^{1}=0\) と表せるから, 式 (186-b) の第 １ 式に代入すると,
\begin{equation}
x^{1}\cosh\psi – x^{4}\sinh\psi=0\quad\rightarrow\quad
x^{1}=\frac{\sinh\psi}{\cosh\psi}x^{4}=\tanh\psi\ x^{4}
\end{equation}
x^{1}\cosh\psi – x^{4}\sinh\psi=0\quad\rightarrow\quad
x^{1}=\frac{\sinh\psi}{\cosh\psi}x^{4}=\tanh\psi\ x^{4}
\end{equation}
これは \(x^{4}\) 軸からの傾きが \(\tanh\psi\) であるような原点を通る直線である．従って, 座標系 \((x’^{1},x’^{4})\) は, 直交座標系 \((x^{1},x^{4})\) に対して「斜交座標系」となることが分かる(下図 1 を参照)．
図 1. ２つの双曲線は, 原点からの世界距離が \(1\) となる場所 (世界線) を表している．また双曲線の漸近線は, 速さ \(c\) で進行する光の世界線になっている．グラフは \(\beta=0.2\) 即ち \(v=0.2c\) の場合である．
References
| ↑1 | [ブログ註] 式 \((II)\) の不変量 \(s^2\) は, 事象の起った点 \(x_i\) と原点 \(O\) の「4元的距離の2乗」と呼ばれる． |
|---|---|
| ↑2 | [ブログ註] (ランダウ：「場の古典論」§2 を参考) 一定の速度で相対運動している基準系 \(K\) を考える．\(K\) 系での座標が \((x_1,y_1,z_1)\) の点からこの系の時刻 \(t_1\) に「光速度で進む信号を送り出すこと」を第1 の事象とする．座標 \((x_2,y_2,z_2)\) の点に信号が時刻 \(t_2\) に到達することを事象2 とする．これらの世界点を \(P\) 及び \(Q\) とすると, これら ２つの異なる世界点に対して \[s_{12}=\sqrt{c^{2}(t_2-t_1)^{2}-(x_2-x_1)^{2}-(y_2-y_1)^{2}-(z_2-z_1)^{2}}\] という量は 2事象間の「世界距離」と呼ばれる．\(K\) 系に於ける ２つの事象の 4元座標の間の関係は,次のように書くことが出来る： \[(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2-c^2(t_2-t_1)^2=0\] 従って, ２つの異なる世界点の間の世界間隔はゼロに成り得る．すなわち,「光の世界線」上の ２点間は世界距離がすべてゼロになっている．このような空間の幾何学は「擬ユークリッド幾何学」と言われる． |
| ↑3 | \(\mathit{Math.}\ \) \(\mathit{Ann.},\ \) \(\mathbf{68}\ \) (1910)\(\ \) 526 |
| ↑4 | [ブログ註] 式 \((I)\) で \(x’=0\) とおくと \(x-vt=0\) より \(x/t=v\) である．また, 式 (186-a) で \(x’^{1}=0\) とおくと, \begin{equation*} ．x^{1}\cos\phi+x^{4}\sin\phi=0\ \rightarrow\ x\cos\phi + ict\,\sin\phi=0 \ \rightarrow\ x+ict\,\tan\phi=0\ \rightarrow\ \tan\phi = \frac{-x}{ict}=i\frac{x/t}{c}=i\frac{v}{c}=i\beta \end{equation*} |
| ↑5 | [ブログ註] Minkowski 空間自身は, 完全なユークリッド空間ではないので「擬ユークリッド空間」と呼ばれるが, 斜交系ではないので注意する． |
