\(\)
J.J.Sakurai では, 角運動量を「回転の生成演算子」として導入している．それに対してランダウは「力学・場の理論」§9及び「量子力学」§14に於いて, 角運動量を「空間の等方性」に起因する保存量として導入している．物理的にはこちらの方が分かり易いのではないかと思われるので紹介しておこう．
古典力学での角運動量
「空間の等方性」に起因する保存則を導こう．この「等方性」というのは,「(\(N\)個の質点からなる)孤立した力学系の性質が, 空間内で系全体が任意回転しても変わらない」ということである．そこで系の無限に小さな回転を考え, その際にラグランジアンが不変であるための条件を求めよう．
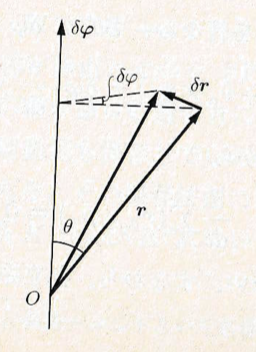
無限小回転のベクトル \(\delta\vec{\phi}\) を導入する．このベクトルの大きさは回転角 \(\delta\phi\) に等しく, その方向は回転軸に一致している．
まず初めに, (回転軸上にある)座標原点から, 回転している系の任意の質点 \(a\) に向かう位置ベクトル \(\mathbf{r}_a\) を考える．回転に際しての \(\mathbf{r}_a\) の変化量 \(\delta\mathbf{r}_a\) を求める．位置ベクトル \(\mathbf{r}\) の先端の変位の大きさと角度の間には次の関係がある(図1を参照)：
\begin{equation}
\def\mb#1{\mathbf{#1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
|\delta\mb{r}|=r\sin\theta\cdot\delta\phi
\tag{1}
\end{equation}
\def\mb#1{\mathbf{#1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
|\delta\mb{r}|=r\sin\theta\cdot\delta\phi
\tag{1}
\end{equation}
図 1 .
このベクトル \(\delta\mb{r}\) の方向は \(\mb{r}\) と \(\delta\vec{\phi}\) とで張られる平面に対して垂直であるから, 位置ベクトル \(\mb{r}_a\) について次が言えることは明らかである：
\begin{equation}
\delta\mb{r}_a = \delta\vec{\phi}\times\mb{r}_a
\tag{2}
\end{equation}
\delta\mb{r}_a = \delta\vec{\phi}\times\mb{r}_a
\tag{2}
\end{equation}
系の回転に際しては, 位置ベクトルの方向が変わるだけでなく, 力学系の全ての粒子の「速度の方向」も変化する．その際,「全てのベクトルは同じ法則に従って変換される」ことに注意する．従って, 各々の速度 \(\mb{v}_a\) の増加分(変化量)を静止した座標系で書くと次となる：
\begin{equation}
\delta\mb{v}_a = \delta\vec{\phi}\times \mb{v}_a
\tag{3}
\end{equation}
\delta\mb{v}_a = \delta\vec{\phi}\times \mb{v}_a
\tag{3}
\end{equation}
これらの表現を,「回転に対してラグランジアン \(L\) が不変」という次の条件に代入する：
\begin{equation}
\delta L = \sum_{a} \left(\ppdiff{L}{\mb{r}_a}\cdot\delta\mb{r}_a + \ppdiff{L}{\mb{v}_a}\cdot\delta\mb{v}_a\right)=0
\tag{4}
\end{equation}
\delta L = \sum_{a} \left(\ppdiff{L}{\mb{r}_a}\cdot\delta\mb{r}_a + \ppdiff{L}{\mb{v}_a}\cdot\delta\mb{v}_a\right)=0
\tag{4}
\end{equation}
このとき, 一般化運動量の定義とラグランジュの運動方程式から,
\begin{equation}
\ppdiff{L}{\mb{v}_a}=\ppdiff{L}{\dot{\mb{r}}_a}=\mb{p}_a,\quad \ppdiff{L}{\mb{r}_a}=\frac{d}{dt}\left(\ppdiff{L}{\dot{\mb{r}}_a}\right)=\frac{d}{dt}\left(\ppdiff{L}{\mb{v}_a}\right)=\frac{d}{dt}\mb{p}_a=\dot{\mb{p}}_a
\tag{5}
\end{equation}
\ppdiff{L}{\mb{v}_a}=\ppdiff{L}{\dot{\mb{r}}_a}=\mb{p}_a,\quad \ppdiff{L}{\mb{r}_a}=\frac{d}{dt}\left(\ppdiff{L}{\dot{\mb{r}}_a}\right)=\frac{d}{dt}\left(\ppdiff{L}{\mb{v}_a}\right)=\frac{d}{dt}\mb{p}_a=\dot{\mb{p}}_a
\tag{5}
\end{equation}
この式 (5) 及び式 (2) と式 (3) を, 式 (4) に代入すると次となる：
\begin{equation}
\delta L = \sum_a \left\{ \dot{\mb{p}}_a\cdot(\delta\vec{\phi}\times\mb{r}_a)
+\mb{p}_a\cdot(\delta\vec{\phi}\times\mb{v}_a)\right\}=0
\tag{6}
\end{equation}
\delta L = \sum_a \left\{ \dot{\mb{p}}_a\cdot(\delta\vec{\phi}\times\mb{r}_a)
+\mb{p}_a\cdot(\delta\vec{\phi}\times\mb{v}_a)\right\}=0
\tag{6}
\end{equation}
３重積の循環置換 \(\mb{A}\cdot(\mb{B}\times\mb{C})=\mb{B}\cdot(\mb{C}\times\mb{A})=\mb{C}\cdot(\mb{A}\times\mb{B})\) を行うと,
\begin{equation*}
\dot{\mb{p}}_a\cdot(\delta\vec{\phi}\times\mb{r}_a)=\delta\vec{\phi}\cdot(\mb{r}_a\times\dot{\mb{p}}_a),\quad
\mb{p}_a\cdot(\delta\vec{\phi}\times\mb{v}_a)=\delta\vec{\phi}\cdot(\mb{v}_a\times\mb{p}_a)
\end{equation*}
\dot{\mb{p}}_a\cdot(\delta\vec{\phi}\times\mb{r}_a)=\delta\vec{\phi}\cdot(\mb{r}_a\times\dot{\mb{p}}_a),\quad
\mb{p}_a\cdot(\delta\vec{\phi}\times\mb{v}_a)=\delta\vec{\phi}\cdot(\mb{v}_a\times\mb{p}_a)
\end{equation*}
そこで更に \(\delta\vec{\phi}\) を括り出すと,
\begin{align}
\delta L &= \sum_a\left\{\delta\vec{\phi}\cdot(\mb{r}_a\times\dot{\mb{p}}_a)
+\delta\vec{\phi}\cdot(\mb{v}_a\times\mb{p}_a)\right\}\notag\\
&=\delta\vec{\phi}\cdot\sum_a\left\{\mb{r}_a\times\dot{\mb{p}}_a+\mb{v}_a\times\mb{p}_a\right\}\notag\\
&=\delta\vec{\phi}\cdot\sum_a\left\{\mb{r}_a\times\frac{d}{dt}\mb{p}_a
+\frac{d}{dt}\mb{r}_a\times\mb{p}_a\right\}\notag\\
&=\delta\vec{\phi}\cdot\sum_a\frac{d}{dt}\big(\mb{r}_a\times\mb{p}_a\big)=0
\tag{7}
\end{align}
\delta L &= \sum_a\left\{\delta\vec{\phi}\cdot(\mb{r}_a\times\dot{\mb{p}}_a)
+\delta\vec{\phi}\cdot(\mb{v}_a\times\mb{p}_a)\right\}\notag\\
&=\delta\vec{\phi}\cdot\sum_a\left\{\mb{r}_a\times\dot{\mb{p}}_a+\mb{v}_a\times\mb{p}_a\right\}\notag\\
&=\delta\vec{\phi}\cdot\sum_a\left\{\mb{r}_a\times\frac{d}{dt}\mb{p}_a
+\frac{d}{dt}\mb{r}_a\times\mb{p}_a\right\}\notag\\
&=\delta\vec{\phi}\cdot\sum_a\frac{d}{dt}\big(\mb{r}_a\times\mb{p}_a\big)=0
\tag{7}
\end{align}
\(\delta\vec{\phi}\) は任意であるから,
\begin{equation}
\sum_a \frac{d}{dt}\big(\mb{r}_a\times\mb{p}_a\big) = \frac{d}{dt}\sum_a \big(\mb{r}_a\times\mb{p}_a\big)=0
\tag{8}
\end{equation}
\sum_a \frac{d}{dt}\big(\mb{r}_a\times\mb{p}_a\big) = \frac{d}{dt}\sum_a \big(\mb{r}_a\times\mb{p}_a\big)=0
\tag{8}
\end{equation}
でなければならない．すなわち, 孤立系の運動に際しては, 次のベクトル量が保存されることが分かった：
\begin{equation}
\mb{M}=\sum_a \big(\mb{r}_a\times\mb{p}_a\big)
\tag{9}
\end{equation}
\mb{M}=\sum_a \big(\mb{r}_a\times\mb{p}_a\big)
\tag{9}
\end{equation}
この量を系の「角運動量」(或いは単に「モーメント」)と呼ぶ [1] 「回転モーメント」, 「角モーメント」という名称も用いられる．．
運動量の場合と同様に, この量の加法性は明らかである．このことは相互作用が有るか無いかに依らない．
量子力学での角運動量
関数 \(f(x)\) の \(x=a\) の近傍, すなわち \(x’=a+\delta x\) でのテイラー展開, または, 関数 \(g(x,y)\) の \((x=a,y=b)\) 近傍, すなわち \((x’,y’)=(a+\delta x, b+\delta y)\) でのテイラー展開は,
\begin{align*}
&f(a+dx)=f(a)+\left(\frac{d f}{dx}\right)_a dx +\frac{1}{2!}\left(\frac{d^{2}f}{dx^{2}}\right)_a (dx)^{2}+\dotsb,\\
&f(a+dx,b+dy)\approx f(a,b)+\left(\ppdiff{f}{x}\right)_a dx +\left(\ppdiff{f}{y}\right)_b dy
\end{align*}
であるから, 式 (2) の回転による変化によって, 任意の多変数関数 \(\psi(\mb{r}_1,\mb{r}_2,\dotsb)\) は次の関数に移る：
\begin{align}
\psi(\mb{r}_1+\delta\mb{r}_1,\mb{r}_2+\delta\mb{r}_2,\dotsb)&\approx \psi(\mb{r}_1,\mb{r}_2,\dotsb)
+\ppdiff{\psi}{\mb{r}_1}\cdot\delta\mb{r}_1+\ppdiff{\psi}{\mb{r}_2}\cdot\delta\mb{r}_2+\dotsb\notag\\
&= \psi(\mb{r}_1,\mb{r}_2,\dotsb)+\sum_a \delta\mb{r}_a\cdot\ppdiff{\psi}{\mb{r}_a}\notag\\
&=\psi+\sum_a \delta\mb{r}_a\cdot\nabla_a\psi\notag\\
&=\psi+\sum_a \big(\delta\vec{\phi}\times\mb{r}_a\big)\cdot\nabla_a\psi\notag\\
&=\psi + \sum_a \delta\vec{\phi}\cdot\big(\mb{r}_a\times\nabla_a\psi\big)\notag\\
&=\psi + \delta\vec{\phi}\cdot\sum_a \mb{r}_a\times\nabla_a \psi\notag\\
&=\Big(1+ \delta\vec{\phi}\cdot\sum_a \mb{r}_a\times\nabla_a\Big)\psi(\mb{r}_1,\mb{r}_2,\dotsb)
\tag{10}
\end{align}
\psi(\mb{r}_1+\delta\mb{r}_1,\mb{r}_2+\delta\mb{r}_2,\dotsb)&\approx \psi(\mb{r}_1,\mb{r}_2,\dotsb)
+\ppdiff{\psi}{\mb{r}_1}\cdot\delta\mb{r}_1+\ppdiff{\psi}{\mb{r}_2}\cdot\delta\mb{r}_2+\dotsb\notag\\
&= \psi(\mb{r}_1,\mb{r}_2,\dotsb)+\sum_a \delta\mb{r}_a\cdot\ppdiff{\psi}{\mb{r}_a}\notag\\
&=\psi+\sum_a \delta\mb{r}_a\cdot\nabla_a\psi\notag\\
&=\psi+\sum_a \big(\delta\vec{\phi}\times\mb{r}_a\big)\cdot\nabla_a\psi\notag\\
&=\psi + \sum_a \delta\vec{\phi}\cdot\big(\mb{r}_a\times\nabla_a\psi\big)\notag\\
&=\psi + \delta\vec{\phi}\cdot\sum_a \mb{r}_a\times\nabla_a \psi\notag\\
&=\Big(1+ \delta\vec{\phi}\cdot\sum_a \mb{r}_a\times\nabla_a\Big)\psi(\mb{r}_1,\mb{r}_2,\dotsb)
\tag{10}
\end{align}
ただし, ３重積の循環置換から
\begin{equation*}
\big(\delta\vec{\phi}\times\mb{r}_a\big)\cdot\nabla_a\psi=\big(\mb{r}_a\times\nabla_a\psi\big)\cdot\delta\vec{\phi}, \quad\rightarrow\quad \big(\delta\vec{\phi}\times\mb{r}_a\big)\cdot\nabla_a\psi=\delta\vec{\phi}\cdot\big(\mb{r}_a\times\nabla_a\psi\big)
\end{equation*}
\big(\delta\vec{\phi}\times\mb{r}_a\big)\cdot\nabla_a\psi=\big(\mb{r}_a\times\nabla_a\psi\big)\cdot\delta\vec{\phi}, \quad\rightarrow\quad \big(\delta\vec{\phi}\times\mb{r}_a\big)\cdot\nabla_a\psi=\delta\vec{\phi}\cdot\big(\mb{r}_a\times\nabla_a\psi\big)
\end{equation*}
を用いている．
このときの表式
\begin{equation}
\mathscr{D}(\delta\vec{\phi})=1+i\delta\vec{\phi}\cdot\mb{G}=1+\delta\vec{\phi}\cdot\sum_a \mb{r}_a\times\nabla_a
\tag{11}
\end{equation}
\mathscr{D}(\delta\vec{\phi})=1+i\delta\vec{\phi}\cdot\mb{G}=1+\delta\vec{\phi}\cdot\sum_a \mb{r}_a\times\nabla_a
\tag{11}
\end{equation}
は, 式 (2) から「無限小回転の演算子」と考えることが出来る．「無限小回転が系のハミルトニアンを変化させない」という事実は, 回転演算子と演算子 \(\hat{H}\) の可換性によって表現される：
\begin{equation*}
\mathscr{D}(\delta\vec{\phi})\hat{H}-\hat{H}\mathscr{D}(\delta\vec{\phi})=0
\end{equation*}
\mathscr{D}(\delta\vec{\phi})\hat{H}-\hat{H}\mathscr{D}(\delta\vec{\phi})=0
\end{equation*}
\(\delta\vec{\phi}\) は定ベクトルであるから, この条件は演算子 \(\sum_a \mb{r}_a\times\nabla_a\) とハミルトニアン \(\hat{H}\) との可換性にまとめられる：
\begin{equation}
\Big(\sum_a \mb{r}_a\times\nabla_a\Big)\hat{H}-\hat{H}\Big(\sum_a \mb{r}_a\times\nabla_a\Big)=0
\tag{12}
\end{equation}
\Big(\sum_a \mb{r}_a\times\nabla_a\Big)\hat{H}-\hat{H}\Big(\sum_a \mb{r}_a\times\nabla_a\Big)=0
\tag{12}
\end{equation}
これは,「ある保存則」を表している．
閉じた系については, 空間の等方性からその保存性が導かれる量が系の「角運動量」である(上記古典力学の場合を見よ)．従って,「演算子 \(\displaystyle{i\mb{G}=\frac{i}{\hbar}\hat{\mb{L}}=\sum_a \mb{r}_a\times\nabla_a}\) は, 定係数を除いて系の運動の全角運動量に, また和の各項 \(\mb{r}_a\times\nabla_a\) は, 個別粒子の角運動量に対応しなければならない」．「比例定数は \(-i\hbar\) に等しいと置かなければならない」．こうすれば粒子の角運動量演算子 \(\hat{\mb{l}}=-i\hbar\mb{r}\times\nabla=\mb{r}\times\hat{\mb{p}}\) の表式が, 通常の古典的表式 \(\mb{r}\times\mb{p}\) に正確に対応する．以下では, いつも \(\hbar\) を単位にして測った角運動量を用いることにしよう．このように定義した個別粒子の角運動量を \(\hat{\mb{l}}\) で表わし, 系全体の角運動量を \(\hat{\mb{L}}\) で表わすことにしよう．従って, 系全体の角運動量演算子および各粒子の角運動量演算子としては次式が得られる：
\begin{equation}
\hat{\mb{L}}=\sum_a \hbar\hat{\mb{l}}_a=\sum_a \mb{r}_a\times\big(-i\hbar\nabla_a\big)=\sum_a \mb{r}_a\times\hat{\mb{p}}_a,\quad
\hbar\hat{\mb{l}}_a=\mb{r}_a\times\hat{\mb{p}}_a=-i\hbar\mb{r}_a\times\nabla_a,
\tag{13}
\end{equation}
\hat{\mb{L}}=\sum_a \hbar\hat{\mb{l}}_a=\sum_a \mb{r}_a\times\big(-i\hbar\nabla_a\big)=\sum_a \mb{r}_a\times\hat{\mb{p}}_a,\quad
\hbar\hat{\mb{l}}_a=\mb{r}_a\times\hat{\mb{p}}_a=-i\hbar\mb{r}_a\times\nabla_a,
\tag{13}
\end{equation}
或いは, 各粒子の角運動量演算子を成分で表わすと次となる：
\begin{equation}
\hbar\hat{l}_x = y\hat{p}_z-z\hat{p}_y,\quad \hbar\hat{l}_y=z\hat{p}_x-x\hat{p}_z,\quad
\hbar\hat{l}_z=x\hat{p}_y-y\hat{p}_x
\tag{14}
\end{equation}
\hbar\hat{l}_x = y\hat{p}_z-z\hat{p}_y,\quad \hbar\hat{l}_y=z\hat{p}_x-x\hat{p}_z,\quad
\hbar\hat{l}_z=x\hat{p}_y-y\hat{p}_x
\tag{14}
\end{equation}
References
| ↑1 | 「回転モーメント」, 「角モーメント」という名称も用いられる． |
|---|
