水素原子スペクトルの微細構造


ファインマンは, 第９講 (Ninth Lecture) の最初の問題の直前で次のように書いていた：

次に $E=mc^{2}+W$ と置く．ただし $W\ll mc^{2}$ である．そして $V=Ze^{2}/r$ を代入すると,

\begin{equation}
(W-V)\chi + \frac{\hbar^{2}}{2m}\nabla \chi = -\frac{(W-V)^{2}}{2m}\chi
\tag{9-2”}
\end{equation}

左辺第1項との比較から右辺の項を無視すると, 通常のシュレディンガー方程式となる．$(W-V)^2/2mc^2$ を摂動ポテンシャル $\Delta V$ とすることで, 学生諸君は水素原子スペクトルの微細構造を得て, それを正確な数値と比較すべきである．

そこで, シュポルスキー：「原子物理学」§ 204 微細構造の公式の文章や, シッフ：「量子力学」の文章の抜粋を示すことで, この課題の解答としようと思う．

微細構造の公式

ケプラー問題をディラック方程式を用いて解くと, バルマーのエネルギー準位以外にその補正項が得られる．この補正項は「微細構造の公式」と呼ばれている．この補正項をディラック方程式に依らず, 初等的なやり方で導出してみる．
シュレディンガー方程式によるケプラー問題を解く際に, さらに次の2つの重要な因子を考慮する必要がある：

質量の速度に対する相対論的依存性．
スピンの存在．

これら２つの因子の各々に対して, この問題の古典論的ハミルトニアン関数に於ける付加項が対応する．

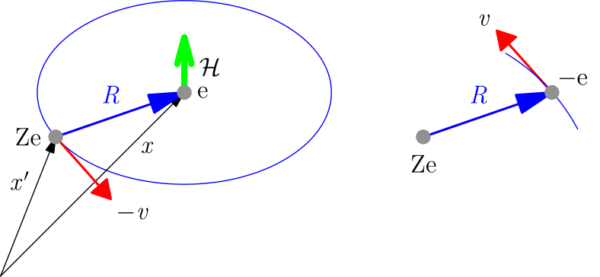
質量の速度に対する依存性の考慮に関連した付加項の起源は,「電子の相対論的運動は,ケプラー楕円運動 $H_0$ に歳差運動 $H_r$ が付随したものとなる」ことによる：

\begin{equation*}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\half{\frac{1}{2}}
H=H_0 + H_r,\quad
H_0=\frac{1}{2\mu_0}\left(p_r^{2}+\frac{1}{r^{2}}p_{\phi}^{2}\right)-\frac{Ze^{2}}{r}
\end{equation*}

ただし $\mu_0$ は静止質量であり, $H_r$ は相対論的歳差運動に対応した付加的なエネルギーである．
スピンと関連した磁気モーメントの存在のために, 電子はその「軌道運動」によって生じている磁場中に在る「磁気双極子」として振る舞う．即ち磁気的相互作用の補足的なエネルギーを持っている．この付加項を「スピン-軌道相互作用」のエネルギー $H_{ls}$ という．

従って, 全ハミルトニアン関数は次の3項から構成される：

\begin{equation*}
H = H_0 + H_r + H_{ls}
\end{equation*}

その際に $H_0$ はエネルギーの主要部分即ち「バルマー項」を与える．そして $H_r$ と $H_{ls}$ は小さい「摂動」と考えることが出来, これがスペクトル項 $T_0$ に補正 $\Delta T$ を与える：

\begin{equation*}
T_0=T(n)\equiv -\frac{E_n}{hc},\quad\rightarrow\quad T_0 + \Delta T,\quad
\Delta T = \Delta T_r + \Delta T_{ls}
\end{equation*}

まず, 相対論的な補正 $\Delta T_r$ を摂動論を用いて計算すると次の公式が得られる：

\begin{equation*}
\Delta T_r = \frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{l+\frac{1}{2}}-\frac{3}{4n}\right)
\tag{204.1}
\end{equation*}

ただし $R$ は「リュードベリ定数」,そして$\alpha$は「微細構造定数」である：

\begin{equation*}
R=\frac{me^{4}}{4\pi\hbar^{3}c}=109,737.303\,\mathrm{cm}^{-1},\quad
\alpha=\frac{e^{2}}{\hbar c}=\frac{1}{137}
\end{equation*}

さて, 今度は第２の補正, すなわち「スピンと軌道角運動量との間の相互作用による補正」の考察に向かおう．その補正を半古典論的な考察によって求めよう．電子の軌道運動によって作られる磁場中に於ける磁石としての電子が持つ付加的なエネルギーを,「磁場中に置かれた磁気双極子の位置エネルギー $V = −\mb{M}\cdot\mb{\mathcal{H}}$」として計算しよう．ここで $\mb{M}$ は電子の固有磁気モーメントであり, $\mb{\mathcal{H}}$ は電子の軌道運動によって生じる磁場の強さである．磁場の強さの値 $\mathcal{H}$ は次のようにして計算できる．核と結び付いた「動かない」座標系から, 電子と一緒に動く座標系に移ろう．この座標系では電子の重心は静止しており, 核 $Ze$ は電子の速度 $\mb{v}$ と絶対値は等しいが方向は反対の速度 $-\mb{v}$ で運動している．この運動は強さ $Ze\mb{v}$ の電流を生じる (図 3.1参照)．「ビオ-サバールの法則」から,
\begin{align*}
\mb{H}(\mb{x})&=\frac{1}{c}\int_{-\infty}^{\infty}
\frac{\mb{j}(\mb{x}’)\times(\mb{x}-\mb{x}’)}{|\mb{x}-\mb{x}’|^{3}}\,d^{3}x’, \quad \mathrm{or}\quad
\overline{\mb{\mathcal{H}}}=\frac{1}{c}\int \frac{\overline{\mb{j}}(\mb{x}’)\times\mb{R}}{R^{3}}\,dV’\notag\\
\overline{\mb{\mathcal{H}}}&=\frac{1}{c}\int \frac{\overline{\mb{j}}\times\mb{R}}{R^{3}}\,dV
=\left(\int \frac{\mb{j}}{R}\,dV\right)\times\frac{\mb{R}}{c R^{2}},
\quad \int \frac{\mb{j}}{R}dV=\frac{Ze(-\mb{v})}{R}\notag\\
\quad&\rightarrow\quad
\overline{\mb{\mathcal{H}}}=\frac{(-Ze\mb{v})}{R}\times\frac{\mb{R}}{cR^{2}}
=-\frac{Ze}{cR^{3}}\mb{v}\times\mb{R}
\end{align*}
よって電子が存在する場所 $\mb{r}=\mb{R}$ に於いて, 電流 $(-Ze\mb{v})$ が生起する磁場は次である：

\begin{equation}
\mb{\mathcal{H}}=-\frac{Ze}{cr^{3}}\mb{v}\times\mb{r}=\frac{Ze}{cr^{3}}\mb{r}\times\mb{v}
\tag{204.3}
\end{equation}

図 3-1. 電子から見たとき, 核 $Ze$ は電子に対し周回しているので, 磁場 $\mathcal{H}$ を電子の位置に生起する．

ベクトル積 $\mb{r}\times\mb{v}$ は, 容易に角運動量 $\mb{L}$ を使って表される．つまり, 質量 $\mu$ の電子の角運動量は

\begin{equation}
\mb{L}=\mu\,\mb{r}\times\mb{v}
\tag{204.4}
\end{equation}

であることを考慮に入れると, 次が得られる：

\begin{equation}
\mb{\mathcal{H}}=\frac{Ze}{cr^{3}\mu}\mu \mb{r}\times\mb{v}=\frac{Ze}{\mu cr^{3}}\mb{L}
\tag{204.5}
\end{equation}

場 $\mb{\mathcal{H}}$ 中の磁気モーメント $\mb{M}$ の双極子の持つエネルギーは $-\mb{M}\cdot\mb{\mathcal{H}}$ であるから, 付加的エネルギーは次で与えられる：

\begin{equation}
-\mb{M}\cdot\mb{\mathcal{H}}=-\mb{M}\cdot\left(\frac{Ze}{\mu cr^{3}}\mb{L}\right)
=-\frac{Ze}{\mu cr^{3}}\mb{M}\cdot\mb{L}
\tag{204.6}
\end{equation}

この式は, 同時に電子のラーモア歳差運動の運動エネルギーにも等しくなっている．しかし, 式 (204.6) で表されているエネルギーは「電子の重心」が静止している様な座標系に於けるラーモアの歳差運動に対応していることを念頭に置く必要がある．「核」が静止している様な座標系, あるいはもっと正確に言えば「原子全体の重心」が静止している様な座標系に戻るためには, もう一度ローレンツ変換をする必要がある．最終結果として得られる磁気的相互作用の付加エネルギーは, J.I.フレンケルが示したところによれば, 式 (204.6) の半分に等しい．すなわち,

\begin{equation}
H_{ls}=-\frac{Ze}{2\mu c r^{3}}\mb{M}\cdot\mb{L}
\tag{204.7}
\end{equation}

この付加エネルギーを, ハミルトニアン関数の主要部分 $H_0$ に対する小さな「摂動」と考えることが出来る．摂動理論によれば, 摂動によって生じる付加エネルギーはハミルトン関数の摂動項を無摂動状態で平均した「平均値」に等しい．すなわち,

\begin{equation*}
\Delta E_{ls}=\overline{H_{ls}}
\end{equation*}

式 (204.7) に含まれている量は $r$ を除けば全て定数であるから, 平均はただ $1/r^{3}$ についてだけ取ればよい：

\begin{equation}
\Delta E_{ls}=-\frac{Ze}{2\mu c}\overline{\left(\frac{1}{r^{3}}\right)}\,\mb{M}\cdot\mb{L}
\tag{204.8}
\end{equation}

平均は無摂動状態についてとられるのであるから, その計算の実行のためには, ケプラー問題の固有関数を用いる必要がある：

\begin{equation*}
\overline{\left(\frac{1}{r^{3}}\right)}=\int \psi^{*}_{nl}\,\frac{1}{r^{3}}\,\psi_{nl}\,d\tau
\end{equation*}

その計算の結果, 次式が得られる：

\begin{equation}
\overline{\left(\frac{1}{r^{3}}\right)}=\frac{Z^{3}}{\ds{a_{1}^{3}n^{3}l\left(l+\frac{1}{2}\right)(l+1)}}
\tag{204.9}
\end{equation}

ただし $a_{1}$ は「第１ボーア半径」であって, 次に等しい：

\begin{equation}
a_1=\frac{\hbar^{2}}{\mu e^{2}}=0.528\times 10^{-8}\ \mathrm{cm}
\tag{204.10}
\end{equation}

さて今度は, 式 (204.8) に含まれているスカラー積 $\mb{M}\cdot\mb{L}$ の計算に向かおう．スピンに対応する磁気モーメント $\mb{M}$ とスピン角運動量 $\mb{S}$ との比は $\displaystyle 2\times\frac{e}{2\mu c}=\frac{e}{\mu c}$ に等しい．$\mb{M}$ の方向は, 電子の電荷がマイナスであるから $\mb{S}$ とは反対向きである．よって,

\begin{equation}
\mb{M}=-\frac{e}{\mu c}\mb{S}
\tag{204.11}
\end{equation}

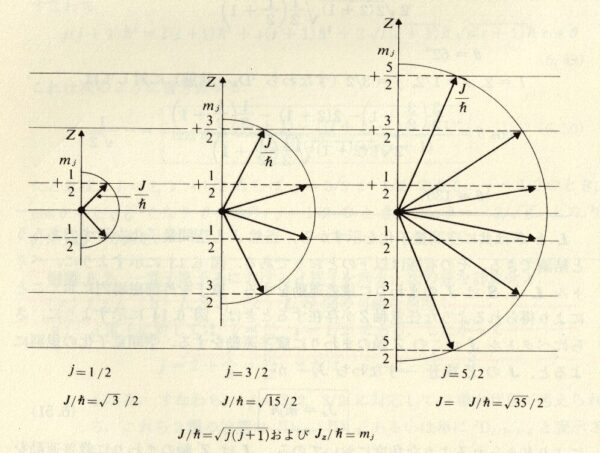
スピン角運動量および軌道角運動量の数値は次に等しい：

\begin{equation}
|\mb{S}|=\hbar\sqrt{s(s+1)},\quad |\mb{L}|=\hbar\sqrt{l(l+1)}
\tag{204.12,13}
\end{equation}

記法を簡潔にするために, 今後途中の計算では $\sqrt{s(s+1)}$ 及び $\sqrt{l(l+1)}$ をそれぞれ $s^{*}$ 及び $l^{*}$ と書くことにしよう．式 (204.9) 及び式 (204.11) を式 (204.8) に代入し, 式 (204.10) を $a_1$ に用い, 次の「リュードベり定数」$R$ と「微細構造定数」$\alpha$ を持ち込む：

\begin{equation*}
R=\frac{\mu e^{4}}{4\pi\hbar^{3}c},\quad \alpha=\frac{e^{2}}{\hbar c}
\end{equation*}

すると簡単な運算の後, 次を得るであろう：

\begin{equation}
\Delta E_{ls}=\frac{R\alpha^{2}\hbar c Z^{4}}{2\pi n^{3}\left(l+\frac{1}{2}\right)(l+1)}l^{*}s^{*}
\cos\theta
\tag{204.14}
\end{equation}

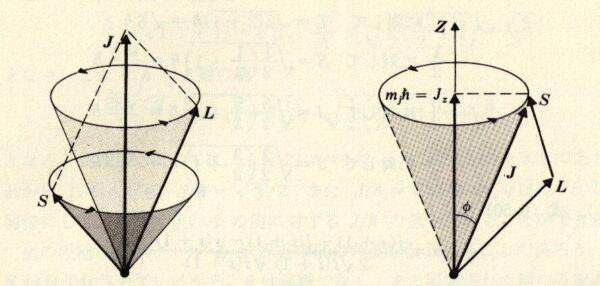
今や最後の段階, すなわち軌道角運動量とスピン角運動量との間の角 $\theta$ の余弦 $\cos\theta$ の計算が残るだけとなった．この計算のためには角運動量 $\mb{L}$ と $\mb{S}$ との合成を考慮する必要がある．

図 3-2. 軌道角運動量ベクトル $\mb{L}$ とスピン角運動量ベクトル $\mb{S}$ は (a) 平行，または (b) 反平行に加えることができる．全角運動量ベクトル $\mb{J}=\mb{L}+\mb{S}$ の大きさは $J=\hbar\sqrt{j(j+1)}$ であり,
(a) $j=l+1/2$ および (b) $j=l-1/2$ である．

角運動量 $\mb{L}$ 及び $\mb{S}$ は決して平行にもならず, それらの間の角度は $0$ とも $\pi$ とも異なることが結論される．次の様な半古典論的な考察方法を用いることが出来る．$\mb{L}$ と $\mb{S}$ とは普通の平行四辺形の規則に従って合成され, その結果, 全角運動量 $\mb{J}$ が得られる．ところがベクトル $\mb{L}$ と $\mb{S}$ とはそれらに対応している磁場を媒介として結び付いているから, それらは $\mb{J}$ に対して, ちょうど弾性的な糸で結ばれている２つのジャイロスコープが, その不変な全角運動量の方向の周りに歳差運動をするのと同じように歳差運動をする．この純然たる「古典論的な」考察の中に,「量子力学」にとって特徴的な次の様な補正が持ち込まれる．第一に $\mb{L}$ と $\mb{S}$ の「方向量子化」の要求によって制限される．すなわちベクトル $\mb{L}$ は $\mb{J}$ に対して, ただ $\mb{J}$ の方向の $\mb{L}$ の成分が $m_{l}\hbar$ に等しくなる様な方向しか取ることが出来ず, ベクトル $\mb{S}$ は, 場の方向の成分が $m_{s}\hbar$ に等しくなる様な方向しか取ることが出来ない．これによって $\mb{L}$ と $\mb{S}$ のなす角度 $\theta$ は飛び飛びの選ばれた値の一組に制限される．第二に, 全角運動量ベクトル $\mb{J}$ の大きさは $j\hbar$ に等しくはなくて $\sqrt{j(j+1)}\hbar$ に等しい．ただし $j=l\pm 1/2$ である．つまり $j$ は全角運動量の量子数なのである．このような考察方法は、明らかに論理的に不完全であるにも関わらず, 驚くべき正確さで正しい結果をもたらす．

図 3-3. 角運動量ベクトル $\mb{L}$ と $\mb{S}$ は, 全角運動量ベクトル $\mb{J}$ の周りを歳差運動する．
右図は, 全角運動量べクトル $\mb{J}$ の空間量子化の様子．

図 3-4. 種々の $j$ の値に対する全角運動量ベクトル $\mb{J}$ の可能な方位．

以上のことを考慮に入れつつ, 今や我々は容易に $\cos\theta$ を計算出来る．三角法の定理によって,

\begin{equation*}
j^{*2}=l^{*2}+s^{*2}-2l^{*}s^{*}\cos(\pi-\theta)
=l^{*2}+s^{*2}+2l^{*}s^{*}\cos\theta
\end{equation*}

よって,

\begin{equation}
l^{*}s^{*}\cos\theta =\frac{j^{*2}-l^{*2}+s^{*2}}{2}
=\half\left\{j(j+1)-l(l+1)-s(s+1)\right\}
\tag{204.15}
\end{equation}

この結果を式 (204.14) に代入すると,

\begin{equation*}
\Delta E_{ls}=\frac{R\alpha^{2}\hbar cZ^{4}}{2\pi n^{3}l\left(l+\half\right)(l+1)}
\frac{j(j+1)-l(l+1)-s(s+1)}{2}
\end{equation*}

が得られる．従って「スピン-軌道相互作用」によるスペクトル項の補正は次となる：

\begin{equation}
\Delta T_{ls}=-\frac{\Delta E_{ls}}{2\pi\hbar c}
=-\frac{R\alpha^{2}Z^{4}}{n^{3}l\left(l+\half\right)(l+1)}\frac{j(j+1)-l(l+1)-s(s+1)}{2}
\tag{204.16}
\end{equation}

$j$ の値は $j=l+1/2$ 及び $j=l-1/2$ のみをとるから,

\begin{equation*}
\frac{j(j+1)-l(l+1)-s(s+1)}{2}=\begin{cases} \ds{\frac{l}{2}} & :\quad j=l+\half \\
\ds{-\frac{l+1}{2}} & :\quad j=l-\half \end{cases}
\end{equation*}

従って, 式 (204.16) は次のような２つの値を持つ：

\begin{equation}
\Delta T_{ls}=\begin{cases}
\ds{-\frac{R\alpha^{2}Z^{4}}{n^{3}2\left(l+\half\right)(l+1)}} & :\quad j=l+\half \\
\ds{+\frac{R\alpha^{2}Z^{4}}{n^{3}2l\left(l+\half\right)}} & :\quad j=l-\half
\end{cases}
\tag{204.17}
\end{equation}

スペクトル項の全補正を求めるには, 式 (204.1) による相対論的補正 $\Delta T_{r}$ と式 (204.17) による補正 $\Delta T_{ls}$ との和を見出すべきである．その結果は次となる：

$j=l+1/2$ に対して( $l=j-1/2$),
\begin{align*}
\Delta T = \Delta T_r + \Delta T_{ls}&=\frac{R\alpha^{2}Z^{4}}{n^{3}}
\left(\frac{1}{l+\half}-\frac{3}{4n}\right)
-\frac{R\alpha^{2}Z^{4}}{2n^{3}\left(l+\half\right)(l+1)}\\
&=\frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{l+1}-\frac{3}{4n}\right)
=\frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{j-\half+1}-\frac{3}{4n}\right)
\end{align*}
$j=l-1/2$ に対して ($l=j+1/2$),
\begin{align*}
\Delta T = \Delta T_r + \Delta T_{ls}&=\frac{R\alpha^{2}Z^{4}}{n^{3}}
\left(\frac{1}{l+\half}-\frac{3}{4n}\right)
+\frac{R\alpha^{2}Z^{4}}{n^{3}2l\left(l+\half\right)}\\
&=\frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{l}-\frac{3}{4n}\right)
=\frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{j+\half}-\frac{3}{4n}\right)
\end{align*}

これらは $j=l\pm\half$ であることに留意すると一つにまとめることが出来る．そのとき両方のカッコ中の第1項の分母は共に $j+\half$ となるので, 次の結果となる：

\begin{equation}
\Delta T = \frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{j+\half}-\frac{3}{4n}\right)
\tag{204.18}
\end{equation}

この式から $j$ がただ一つの値を持っているだけの $S$ 項 ($n=1$ の場合) に対しては, 条件 $\displaystyle \left[ n-j\ge \half,\,j\ge\half\right]$ から, 補正はただ一つの値 $(j=1/2)$ しか持たないことが分かる：

\begin{equation*}
\Delta T = \frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{\half+\half}-\frac{3}{4n}\right)
= \frac{R\alpha^{2}Z^{4}}{n^{3}}\left(1-\frac{3}{4n}\right)
\end{equation*}

従って補正は $S$ 項をずらせるだけで, それを分岐させないことが分かる．その他 ($n=2,3,4,\dotsb$) の項 $(P,D,F,\dotsb)$ に対しては $j$ は2つずつの値 $l\pm1/2$ を持ち, 従ってこれらの項に対応する各エネルギー準位は２つの副準位に分かれる．更に, 主量子数が $n=2$ の際には２つの準位 $2S$ 及び $2P$ があり, 分岐は３つの副準位 (１つの$S$ 項と２つの $P$項) を与える．しかしこのとき, 条件 $\displaystyle \left[ n-j\ge \half,\,j\ge\half\right]$から, $j$ は $S$ 項 ($l=0$) に対しては値 $1/2$ を持ち, $P$ 項 ($l=1$) に対しては $1/2$ 及び $3/2$ を持つ．このとき, $S$ 項の副準位 $\displaystyle 2S_{1/2}\,(j=0+1/2=1/2)$ と $P$ 項の副準位 $\displaystyle 2P_{1/2}\,(j=1-1/2=1/2)$ とは互いに一致するが, 他方 $2P_{1/2}$ 準位と $2P_{3/2}$ 準位 $(j=1+1/2=3/2)$ とは分岐してしまう．

式 (204.18) から $2P_{3/2}$ 準位と $2P_{1/2}$ 準位を計算してみよう．「リュードベり定数」$R$ と「微細構造定数」$\alpha$ の値を次とする：

\begin{equation*}
R=\frac{\mu e^{4}}{4\pi\hbar^{3}c}=109,737.303\,\mathrm{cm}^{-1},\quad
\alpha=\frac{e^{2}}{\hbar c}=\frac{1}{137},\quad \alpha^{2}=5.32\times10^{-5}
\end{equation*}

すると各準位の補正量 $\Delta T$ は,「波数」として次となる：

$2P_{3/2}$の場合$(n=2,\,l=1,j=1+\half=\frac{3}{2})$： $\displaystyle\quad \Delta T_{3/2}=\frac{R\alpha^{2}}{8}\left(\half -\frac{3}{4\times 2}\right),$
$2P_{1/2}$の場合$(n=2,\,l=1,j=1-\half=\frac{1}{2})$： $\displaystyle\quad \Delta T_{1/2}=\frac{R\alpha^{2}}{8}\left(1 -\frac{3}{4\times 2}\right),$

従って, ２つの分岐量 (補正量の差) は次となる：
\begin{align*}
\Delta =\Delta T_{1/2} – \Delta T_{3/2}&=\frac{R\alpha^{2}}{8}\times \left(1-\half\right)
=\frac{1.09737\times10^{5}\times 5.32\times10^{-5}}{8}\times \half \\
&=0.364\,\mathrm{cm}^{-1}
\end{align*}

[ 参考 ] 上式 (204.1) を示すために, シッフ：「量子力学」§ 51 の文章の抜粋を示す．
電磁ポテンシャル $\mb{A}(\mb{r},t)$, $\phi(\mb{r},t)$ が存在する場合, これを波動方程式の中に取り入れるためには $\phi$ と $(1/c)\mb{A}$ とが $E$ 及び $\mb{p}$ と同一のLorentz変換性を持っていることを利用してやればよい．非相対論的な式 (24.29)

\begin{equation}
H=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^2 +e\phi
\tag{24.29}
\end{equation}

の形から類推して, 電荷 $e$ の粒子に対しては式 (51.2)：$E^{2}=c^2\mb{p}^2 +m^2c^4$ を,

\begin{equation}
(E-e\phi)^2 = (c\mb{p}-e\mb{A})^2 + m^2c^4
\tag{51.9}
\end{equation}

で置き換える．このときの $\mb{p}$ は一般化運動量 $\partial L/\partial \mb{v}$ の方であり, 通常の3次元運動量$m\mb{v}$ではない．そこで, 置き換え $E\to i\hbar\pdiff{t}$, $\mb{p}\to -i\hbar\nabla $ をすると

\begin{equation}
\left(-\hbar^2\frac{\partial^2}{\partial t^2}-2ie\hbar\phi\pdiff{t}
-ie\hbar\ppdiff{\phi}{t}+e^2\phi^2\right)\psi
= \Bigl[-\hbar^2c^2\nabla^2+2ie\hbar c\,\mb{A}\cdot\nabla
+ie\hbar c\,(\nabla\cdot\mb{A})+e^2\mb{A}^2+m^2c^4\Bigr]\psi
\tag{51.10}
\end{equation}

ポテンシャル $\mb{A},\,\phi$ が時間に関係しない場合には, 波動関数 (51.10) は $\mb{r}$と$t$ とに関して分離することが出来る．即ち, その時には

\begin{equation*}
\psi(\mb{r},t)=u(\mb{r})\,e^{-iEt/\hbar}
\end{equation*}

と置いて式 (51.10) に代入する．左辺だけが変わり $\displaystyle i\hbar\pdiff{t}u(\mb{r})e^{-iEt/\hbar}=E\,u(\mb{r})e^{-iEt/\hbar}$ となるので,

\begin{equation}
\bigl(E-e\phi\bigr)^2 u = \Bigl[-\hbar^2c^2\nabla^2+2ie\hbar c\,\mb{A}\cdot\nabla
+ie\hbar c\,(\nabla\cdot\mb{A})+e^2\mb{A}^2+m^2c^4\Bigr]u
\tag{51.12}
\end{equation}

さて次は「$\mb{A}=0$ で, かつ $\phi(\mb{r})$ が球対称, つまり $\phi(\mb{r})=\phi(r)$ という特別な場合」を考えてみる．すると式 (51.12) は

\begin{equation}
\bigl(-\hbar^2c^2\nabla^2+m^2c^4\bigr)u(\mb{r})=\bigl[E-e\phi(r)\bigr]^2 u(\mb{r})
\tag{51.12′}
\end{equation}

となる．これは球座標を使って変数分離が可能であって次となる(シッフ：「量子力学」§14を見よ)：

\begin{align}
&u(r,\theta,\phi)=R(r)Y_{lm}(\theta,\varphi),\notag\\
&\rightarrow\quad
\left[-\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{d}{dr}\right)+\frac{l(l+1)}{r^2}\right]R
=\frac{(E-e\phi)^2-m^2c^4}{\hbar^2c^2}R,\quad l=0,1,2,\dotsb
\tag{51.14}
\end{align}

ここで $E=mc^2+E’$ と置き, さらに $E’$ と $e\phi$ とは $mc^2$ に比べて無視できるものと仮定すると, この式は動径 $r$ に対する非相対論的な方程式に帰着する．そのとき式 (51.14) の右辺の分数部分は当然期待されるように $\displaystyle\frac{2m}{\hbar^2}(E’-e\phi)$ になる．

さらに水素様原子の場合すなわちクーロン場でのエネルギー準位を考えてみる．ポテンシャルを $e\phi=-Ze^2/r$ としたときの式 (51.14) の正確な解は, §16 の結果を使って容易に求められる^[6][ブログ註] シュレディンガー方程式を球座標そして相対座標の表現にすると, 角運動量の量子数 $l$ … Continue reading．式 (51.10) で表される粒子はスピンを持たないから, もちろん電子では有り得ないが, このことを度外視すればこの状況は水素様原子を表していると考えて良い．
$\rho=\alpha r$と置くと, 式 (51.14) は次のようになる：

\begin{align}
&\frac{1}{\rho^2}\frac{d}{d\rho}\left(\rho^2\frac{dR}{d\rho}\right)+
\left[\frac{\lambda}{\rho}-\frac{1}{4}-\frac{l(l+1)-\gamma^2}{\rho^2}\right]R=0,\notag\\
&\qquad\mathrm{where}\quad \gamma\equiv \frac{Ze^2}{\hbar c},\quad
\alpha^2\equiv \frac{4(m^2c^4-E^2)}{\hbar^2c^2},\quad
\lambda\equiv \frac{2E\gamma}{\hbar c\alpha}
\tag{51.15}
\end{align}

$l(l+1)$ が $l(l+1)-\gamma^2$ で置き換えられている点以外は, これはまさしく水素原子に対する式 (16.7) と一致している．パラメータ $\lambda$ は $\rho=\infty$ での $R$ の境界条件で決まり, 式 (51.15) の最後の２式から $\alpha$ を消去すると, $E$ は $\lambda$ によって次のように表される：

\begin{equation}
E=mc^2\left(1+\frac{\gamma^2}{\lambda^2}\right)^{-1/2}
\tag{51.16}
\end{equation}

式 (16.7) の解き方を調べれば分かることだが, $\rho=0$ と $\rho=\infty$ とで式 (51.15) の有限な解が存在するのは

\begin{equation}
\lambda = n’+s+1
\tag{51.17}
\end{equation}

のときに限られる．ただし $n’$ はゼロか正の整数で, $s$ は2次方程式

\begin{equation}
s(s+1)=l(l+1)-\gamma^2
\tag{51.18}
\end{equation}

の解のうち負でないものである．この方程式は２つの解

\begin{equation}
s=-\frac{1}{2}\pm \frac{1}{2}\sqrt{(2l+1)^2 -4\gamma^2}
\tag{51.19}
\end{equation}

を持ち, $l>0$ に対してそのうち一つは正, 他方は負である．

$\sim$ 途中を少し省略する $\sim$．

そこで $l$ の全ての価に対して $+$ の符号を取ると, 式 (51.17) から次となる：

\begin{equation}
\lambda = n’ +\frac{1}{2} +\sqrt{\left(l+\frac{1}{2}\right)^2 -\gamma^2}
\tag{51.20}
\end{equation}

式 (51.16) と式 (51.20) とは式 (16.15) の非相対論的エネルギー準位に対する「微細構造」を与える．これを調べるには, エネルギー準位を表す式を $\gamma^2$ のベキで展開すればよい．この結果を $\gamma^4$ まで取った結果は次のようになる：

\begin{align}
&E=mc^2\left[1-\frac{\gamma^2}{2n^2}-\frac{\gamma^4}{2n^4}
\left(\frac{n}{l+\frac{1}{2}}-\frac{3}{4}\right)\right] \tag{51.21}\\
\rightarrow&\quad W=E-mc^{2}=-\frac{mc^{2}\gamma^{2}}{2n^{2}}
-\frac{mc^{2}\gamma^{4}}{2n^{4}}\left(\frac{n}{l+\frac{1}{2}}-\frac{3}{4}\right)
\tag{51.21′}
\end{align}

ただし, この $\gamma$ は「微細構造定数」と呼ばれ, その大きさは $\gamma\approx 1/137$ である．また $n=n’+l+1$ は全量子数で, 正の整数値を取ることが出来る．式 (51.21) の右辺の第1項は静止エネルギーである．第2項は水素原子に対するエネルギー準位の式 $E_n$ と一致する：

\begin{equation*}
E_{n}^{0}=-\frac{mc^2\gamma^2}{2n^2}=-\frac{mZ^2e^4}{2\hbar^2n^2}
\end{equation*}

第3項は相対論的な補正 $\Delta E_r$ であり, $n$ が同じで $l$ が異なる状態の間に有った縮退が除かれる．式 (51.21) をスペクトル項の公式に変形すると, 上式 (204.1) に一致する：
\begin{align*}
\Delta T_{r}&=-\frac{\Delta E_r}{hc}
=\frac{mc}{4\pi\hbar n^{4}}\left(\frac{Ze^2}{\hbar c}\right)^{4}
\left(\frac{n}{l+\frac{1}{2}}-\frac{3}{4}\right)
=\frac{me^{4}}{4\pi\hbar^{3}c}\cdot\left(\frac{e^{2}}{\hbar c}\right)^{2}\frac{Z^{4}}{n^{4}}
\left(\frac{n}{l+\frac{1}{2}}-\frac{3}{4}\right)\\
&=\frac{R\alpha^{2}Z^{4}}{n^{4}}\left(\frac{n}{l+\frac{1}{2}}-\frac{3}{4}\right)
=\frac{R\alpha^{2}Z^{4}}{n^{3}}\left(\frac{1}{l+\frac{1}{2}}-\frac{3}{4n}\right)
\tag{204.1}
\end{align*}

References[+]

References
↑1	[ブログ註] 「スペクトル項」 $T$ は,「波数」(波長の逆数)を表わす量である．振動数を $\nu$, 光速度を $c$ とするとき, 光の波長 $\lambda$ は $c=\nu\lambda$ の関係にある．光子のエネルギーを $E=h\nu$ とすると, \begin{equation} \frac{1}{\lambda}=\frac{\nu}{c}=\frac{h\nu}{hc}=\frac{E}{hc}, \quad\rightarrow\quad T(n)\equiv -\frac{E_{n}}{hc}\ \mathrm{cm}^{-1} \end{equation} 原子中のエネルギー準位は負の値となるので, スペクトル項は上の波数 $1/\lambda$ の式中のエネルギーにマイナス符号を付けて定義しているのである．
↑2	[ブログ註] ケプラー問題は, シュポルスキーの § 184 に解説されている.
↑3	[ブログ註] 「ゾンマーフェルトの微細構造定数」と呼ばれているこの定数 $\alpha$ は, 極めて注目すべきものである．3つの基本的な普遍定数 $e$, $\hbar$, 及び $c$ の組み合わせであるこの定数が「ディメンションのない数」であることは注目に値する．実際, $e^{2}$ はディメンション [$\mathrm{erg}\times\mathrm{cm}$] を持っている．これは次のことから分かる．$e^{2}/r$ はクーロンの位置エネルギーであり, 従ってエルグを単位として表される．それ故, $[e^{2}]=$[エネルギー$\times$長さ], すなわち [erg$\times$cm]である．$\hbar c$ のディメンションは [エネルギー$\times$時間$\times$速度] である．すなわち \begin{equation} [\hbar c]=\left[\frac{\mathrm{erg}\times\mathrm{sec}\times\mathrm{cm}}{\mathrm{sec}}\right]=[\mathrm{erg}\times\mathrm{cm}]. \end{equation} 結局 $\hbar c$ は $e^{2}$ と同じディメンションを持っている．すなわち $\alpha$ はディメンションの無い量である．$\alpha$ の数値は $e$, $\hbar$, $c$ の数値から求められ, 次のものに等しい： \begin{equation} \alpha=7.0\times10^{-2},\quad \alpha^{2}=5.32\times10^{-5},\quad \frac{1}{\alpha}=137.03, \end{equation}
↑4	[ブログ註] このような置き換えをして,電磁場との相互作用を導入することを「minimalな電磁相互作用を導入する」という．minimal結合を導入する相対論的な処方は, 例えば Claude Itzykson, Jean-Bernard Zuber, Quantum Field Theory の §2-2-3 を参照すべし．
↑5	[ブログ註] 式 (51.12′) を変形すると, \begin{equation} -\nabla u(\mb{r}) = \frac{(E-e\phi)^{2}-m^{2}c^{4}}{\hbar^{2}c^{2}}u(\mb{r}),\quad\rightarrow\quad -\frac{\hbar^{2}}{2m}\nabla u = \frac{(E-e\phi)^{2}-m^{2}c^{4}}{2mc^{2}}u \tag{1} \end{equation} ここで $E=mc^{2}+E’$ と置くと右辺の分子は, \begin{align} (E-e\phi)^{2}-m^{2}c^{4}&=(E’+mc^{2}-e\phi)^{2}-m^{2}c^{4}\\ &=m^{2}c^{4}+2mc^{2}(E’-e\phi)+(E’-e\phi)^{2}-m^{2}c^{4}\\ &=2mc^{2}(E’-e\phi)+(E’-e\phi)^{2} \end{align} 従って, 上式 (1) は \begin{align} -\frac{\hbar^{2}}{2m}\nabla u &= \frac{1}{2mc^{2}}\left\{2mc^{2}(E’-e\phi)+(E’-e\phi)^{2}\right\}u\\ &=(E’-e\phi)u + \frac{(E’-e\phi)^{2}}{2mc^{2}}u\\ \rightarrow &\quad \left[-\frac{\hbar^{2}}{2m}\nabla + e\phi \,-\, \frac{(E’-e\phi)^{2}}{2mc^{2}} \right] u=E’u \end{align} ここで $u\to \chi$, $E’\to W$ と書き換え, そして $V=e\phi$ と置くならば, \begin{equation} \left[-\frac{\hbar^{2}}{2m}\nabla + V \,-\, \frac{(W-V)^{2}}{2mc^{2}} \right] \chi =W\chi, \quad\rightarrow\quad (W-V)\chi + \frac{\hbar^{2}}{2m}\nabla \chi =-\frac{(W-V)^{2}}{2mc^{2}}\chi \end{equation} となり, これは本文の式 (9-2”) に一致することが分かる．
↑6	[ブログ註] シュレディンガー方程式を球座標そして相対座標の表現にすると, 角運動量の量子数 $l$ に対する動径方向の方程式は次となる： \begin{equation} -\frac{\hbar^{2}}{2\mu}\frac{1}{r^{2}}\frac{d}{dr}\left(r^{2}\frac{dR}{dr}\right)-\frac{Ze^{2}}{r}R +\frac{\hbar^{2}}{2\mu}\frac{l(l+1)}{r^{2}}R=ER \tag{16-6} \end{equation} さらに, 無次元の独立変数 $\rho=\alpha r$ となるように次のような $\alpha$ と $\lambda$ を導入する： \begin{equation} \alpha^{2}=\frac{8\mu\|E\|}{\hbar^{2}}\quad\rightarrow\quad \alpha=\sqrt{\frac{8\mu\|E\|}{\hbar^{2}}}, \qquad \lambda=\frac{2\mu Ze^{2}}{\alpha \hbar^{2}}=\frac{Ze^{2}}{\hbar}\sqrt{\frac{\mu}{2\|E\|}} \end{equation} すると方程式 (16-6) はディメンションの無い形に書き直される： \begin{equation} \frac{1}{\rho^{2}}\frac{d}{d\rho}\left(\rho^{2}\frac{dR}{d\rho}\right) +\left(\frac{\lambda}{\rho}-\frac{1}{4}-\frac{l(l+1)}{\rho^{2}}\right)R =0 \tag{16-7} \end{equation}

2024年4月
月	火	水	木	金	土	日
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30