離散フーリエ変換 (DFT)

基準座標の式 (8-77) は, 「デジタル信号処理」(Digital Signal Processing : DSP) に於ける「離散フーリエ変換」(DFT) の式と全く同じ形をしていることに気付いた．従って, 基準座標 $Q_{α}$ は変位 $q_{j}$ のフーリエ変換と見做すことも出来るかも知れない．そこで参考のために, 小畑：「信号処理」の第２章から DFT に関係する部分を抜粋したものに多少の修正を施したものを示しておこう．

サンプリング定理

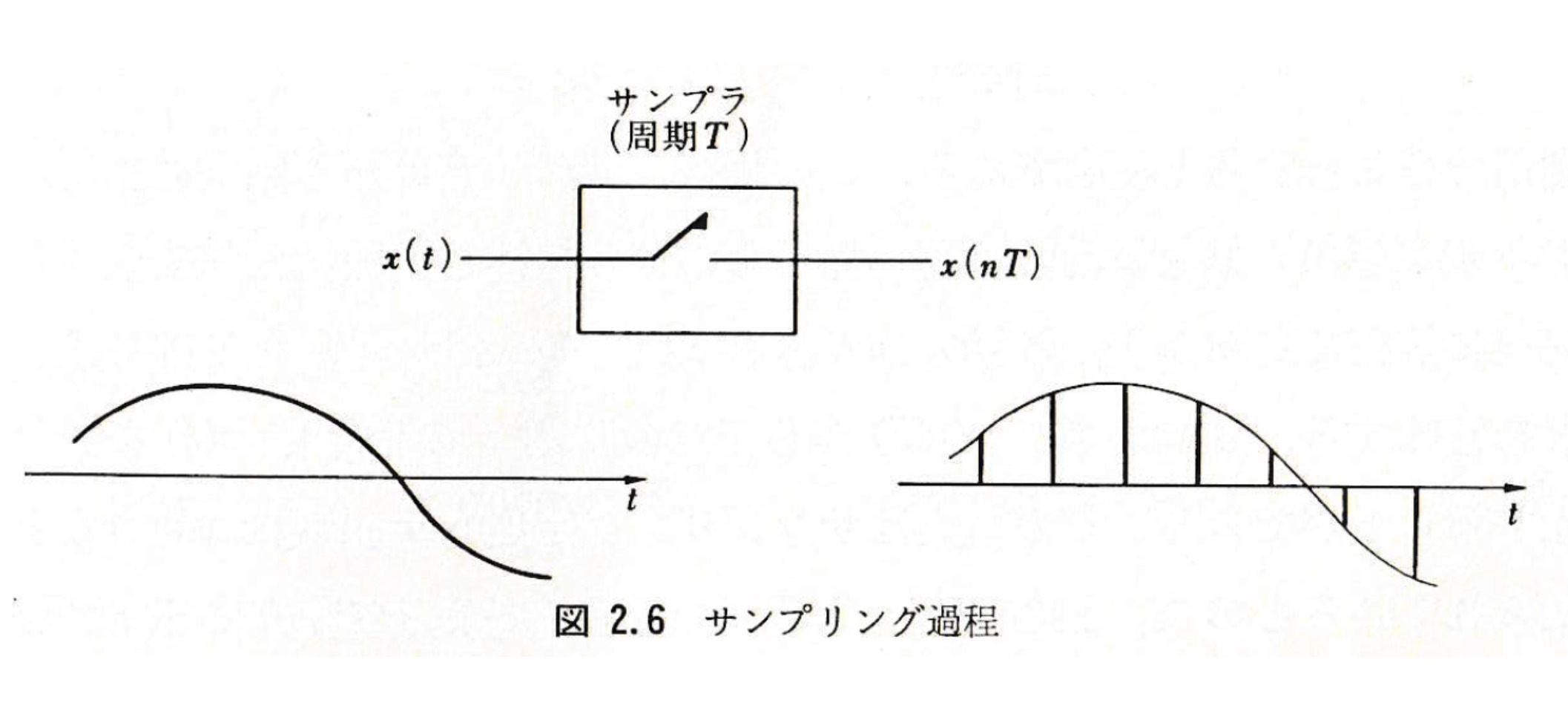
ディジタル信号処理に於いては, 信号 $x (t)$ を一定時間ごとにサンプリングし, そのサンプル値

\begin{matrix} (1) & \dots, x (- T), x (0), x (T), x (2 T), \dots, x (n T), \dots \end{matrix}

を数値に変換してディジタル演算を実行する．この場合, まず時間軸

t

がサンプリング周期

T

によって離散化され, 次に信号値

x (n T)

がアナログ・ディジタル変換の量子化単位

ε

によって離散化される．通常, アナログ・ディジタル変換は実用上十分な精度のものとするので数値化したデータは信号値

x (n T)

をほぼ正確に表現すると考えてよい．ここで問題にするのは, 時間軸

t

を離散化するサンプリング過程, すなわち

x (n T)

に変換する過程である(図 1 を参照)．

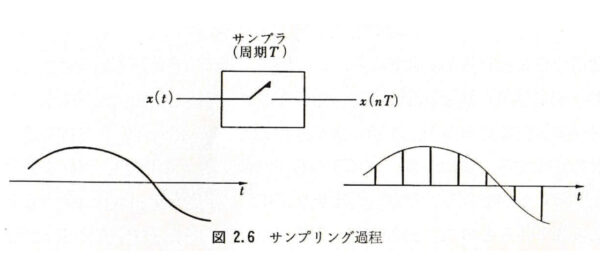
図 1.

信号 $x (t)$ は連続した値をとる時間 $t$ の関数として与えられている．そこから一定時間 $T$ 刻みの値 $x (n T)$ だけを取り出して使用することにすると, 元の信号 $x (t)$ の持っていた情報の一部が失われるのではないか?, 従って, サンプリング過程が不可避であるディジタル信号処理を採用すると近似的な結果しか求めることが出来ないのではないか?, との疑問が発生する．しかし, これは実際問題としては正しくない．我々が取り扱う信号は, 通常, ある周波数以下の成分しか含んでいないので, この性質を利用すると, サンプル値 $x (n T)$ だけ使用して $x (t)$ のスペクトル $X (j ω)$ を正確に求めることが可能である．ただし,「サンプリング周期 $T$ 」は上限周波数から定まるある値以下としなければならない．しかし,「サンプリング時間 $T$ 」を無限に小さくする必要はない．

もちろん, 実際問題としては, 完全に正確なスペクトル $X (j ω)$ を求めるのは困難である．その原因はサンプリング周期 $T$ が有限であるためではなく, 利用できる信号長が有限であるためである．我々は信号 $x (t)$ を $t = - \infty$ から $t = \infty$ までの無限長の時間にわたって観測することは出来ず, ある有限長 $L$ のデータ $x (t)$ $(- \frac{L}{2} \leq t \leq \frac{L}{2})$ しか利用できないからである．

理論的取り扱いとしては, $x (t)$ $(- \infty < t < \infty)$ 或いは, $x (n T)$ $(- \infty < n < \infty)$ が利用できるとすると便利である．この場合, $x (n T)$ だけから完全に正確なスペクトル $X (j ω)$ が求まるが, 信号の時間領域表現 $x (t)$ と周波数領域表現 $X (j ω)$ は完全に等価であるから, $X (j ω)$ が正確に求まることは $x (t)$ も正確に求まることを意味する．すなわち, $x (n T)$ から任意の時刻 $t$ の信号値 $x (t)$ を計算, 復元することが出来る．この事実は「サンプリング定理」として知られているもので, 染谷勲と C.E. Shannon によって独立に研究されたものである．

この信号値系列 $x (n T)$ を, ある形の時間信号 $x_{s} (t)$ として表現することが出来る．この信号 $x_{s} (t)$ は $t = n T$ 以外ではもちろんゼロの値をとる：

\begin{matrix} (2) & x_{s} (t) = 0, t \neq n T, n = 0, \pm 1, \pm 2, \dots \end{matrix}

従って, この信号

x_{s} (t)

は「デルタ関数」を用いて次のように表現することが出来る：

\begin{aligned} x_{s} (t) & = \dots + x (- T) δ (t + T) + x (0) δ (t) + x (T) δ (t - T) + \dots \\ (3) & = \sum_{n = - \infty}^{\infty} x (n T) δ (t - n T) \end{aligned}

このとき,

\begin{aligned} \int_{- \infty}^{\infty} x_{s} (t) d t & = \int_{- \infty}^{\infty} d t {\sum_{n = - \infty}^{\infty} x (n T) δ (t - n T)} \\ (4) & = \sum_{n = - \infty}^{\infty} x (n T) \int_{- \infty}^{\infty} δ (t - n T) d t = \sum_{n = - \infty}^{\infty} x (n T) \end{aligned}

この信号

x_{s} (t)

のフーリエ変換を考える．それを

X_{s} (j ω)

と書くと,

\begin{aligned} X_{s} (j ω) & = \int_{- \infty}^{\infty} x_{s} (t) e^{- j ω t} d t \\ = \int_{- \infty}^{\infty} {\sum_{n = - \infty}^{\infty} x (n T) δ (t - n T)} e^{- j ω t} d t \\ = \sum_{n = - \infty}^{\infty} x (n T) \int_{- \infty}^{\infty} e^{- j ω t} δ (t - n T) d t \\ (5) & = \sum_{n = - \infty}^{\infty} x (n T) e^{- j ω n T} \end{aligned}

もちろん, この

X_{s} (j ω)

のフーリエ逆変換は

x_{s} (t)

となる．

「サンプリング周期 $T$ 」から「サンプリング角周波数 $Ω_{0}$ 」を次とする：

\begin{matrix} (6) & Ω_{0} = \frac{2 π}{T} \end{matrix}

すると,

k

を任意の整数とするならば, 式 (5) から次が言える：

\begin{aligned} X_{s} [j (ω + k Ω_{0})] & = \sum_{n = - \infty}^{\infty} x (n T) e^{- j (ω + k Ω_{0}) n T} \\ = \sum_{n = - \infty}^{\infty} x (n T) e^{- j ω n T} e^{- j k n Ω_{0} T} = \sum_{n = - \infty}^{\infty} x (n T) e^{- j ω n T} e^{- j 2 π k n} \\ (7) & = \sum_{n = - \infty}^{\infty} x (n T) e^{- j ω n T} = X_{s} (j ω) \end{aligned}

従って,「

X_{s} (j ω)

の周期は, サンプリング角周波数

Ω_{0}

に等しい」ことが分かる．このことと, 式 (5) から,

x (n T)

は

X_{s} (j ω)

のフーリエ級数展開の係数になっていると言える：

\begin{matrix} (8) & x (n T) = \frac{1}{Ω_{0}} \int_{- Ω_{0} / 2}^{Ω_{0} / 2} X_{s} (j ω) e^{j n ω T} d ω = \frac{T}{2 π} \int_{- Ω_{0} / 2}^{Ω_{0} / 2} X_{s} (j ω) e^{j n ω T} d ω \end{matrix}

それでは,「原信号

x (t)

のスペクトル

X (j ω)

」は「サンプル信号

x_{s} (t)

のスペクトル

X_{s} (j ω)

」とどのような関係を持っているのであろうか?．

x (t)

のフーリエ変換が

X (j ω)

であるので, その逆変換から

\begin{matrix} (9) & x (t) = \frac{1}{2 π} \int_{- \infty}^{\infty} X (j ω) e^{j ω t} d ω, \to x (n T) = \frac{1}{2 π} \int_{- \infty}^{\infty} X (j ω) e^{j ω n T} d ω \end{matrix}

この

ω

に関する

- \infty

から

\infty

までの積分を, 次のような区間

ω_{k}

に分割して積分することを考える：

k Ω_{0} - \frac{Ω_{0}}{2} \leq ω_{k} \leq k Ω_{0} + \frac{Ω_{0}}{2}, k = 0, \pm 1, \pm 2, \dots

すると, 式 (9) の

x (n T)

は次のように書ける：

\begin{matrix} (10) & x (n T) = \frac{1}{2 π} \sum_{k} \int_{ω_{k}} X (j ω) e^{j ω n T} d ω \end{matrix}

さらに変数変換

ω^{'} = ω - k Ω_{0}

を行うと,

- \frac{Ω_{0}}{2} \leq ω_{k}^{'} \leq \frac{Ω_{0}}{2}, d ω^{'} = d ω, Ω_{0} T = 2 π

となるから,

\begin{aligned} x (n T) & = \frac{1}{2 π} \sum_{k} \int_{- Ω_{0} / 2}^{Ω_{0} / 2} X (j ω^{'} + j k Ω_{0}) e^{j (ω^{'} + k Ω_{0}) n T} d ω^{'} \\ (11) & = \frac{1}{2 π} \int_{- Ω_{0} / 2}^{Ω_{0} / 2} {\sum_{k} X (j ω^{'} + j k Ω_{0})} e^{j ω^{'} n T} d ω^{'} \end{aligned}

この結果を式 (8) と比較すると,次式が言えることが分かる：

\begin{matrix} (12) & X_{s} (j ω) = \frac{1}{T} \sum_{k} X (j ω + j k Ω_{0}) \end{matrix}

従って, 原信号

x (t)

のスペクトル

X (j ω)

を

0, \pm Ω_{0}, \pm 2 Ω_{0}, \dots

だけ位置をずらせて加算したものが

T X_{s} (j ω)

になると言える．よって, 原信号

x (t)

のスペクトル

X (j ω)

が

Ω_{0} / 2

以上の周波数成分を含まない場合には,

- \frac{Ω_{0}}{2} \leq ω \leq \frac{Ω_{0}}{2}

の範囲において

X (j ω)

と

T X_{s} (j ω)

とは完全に一致する．しかしながら,

X (j ω)

が

Ω_{0} / 2

以上の周波数成分を含む場合には, それが

Ω_{0} / 2

以下の周波数成分に重なり合うことになる．この現象を「エイリアシング」(aliasing) と言う (図 2 を参照)．

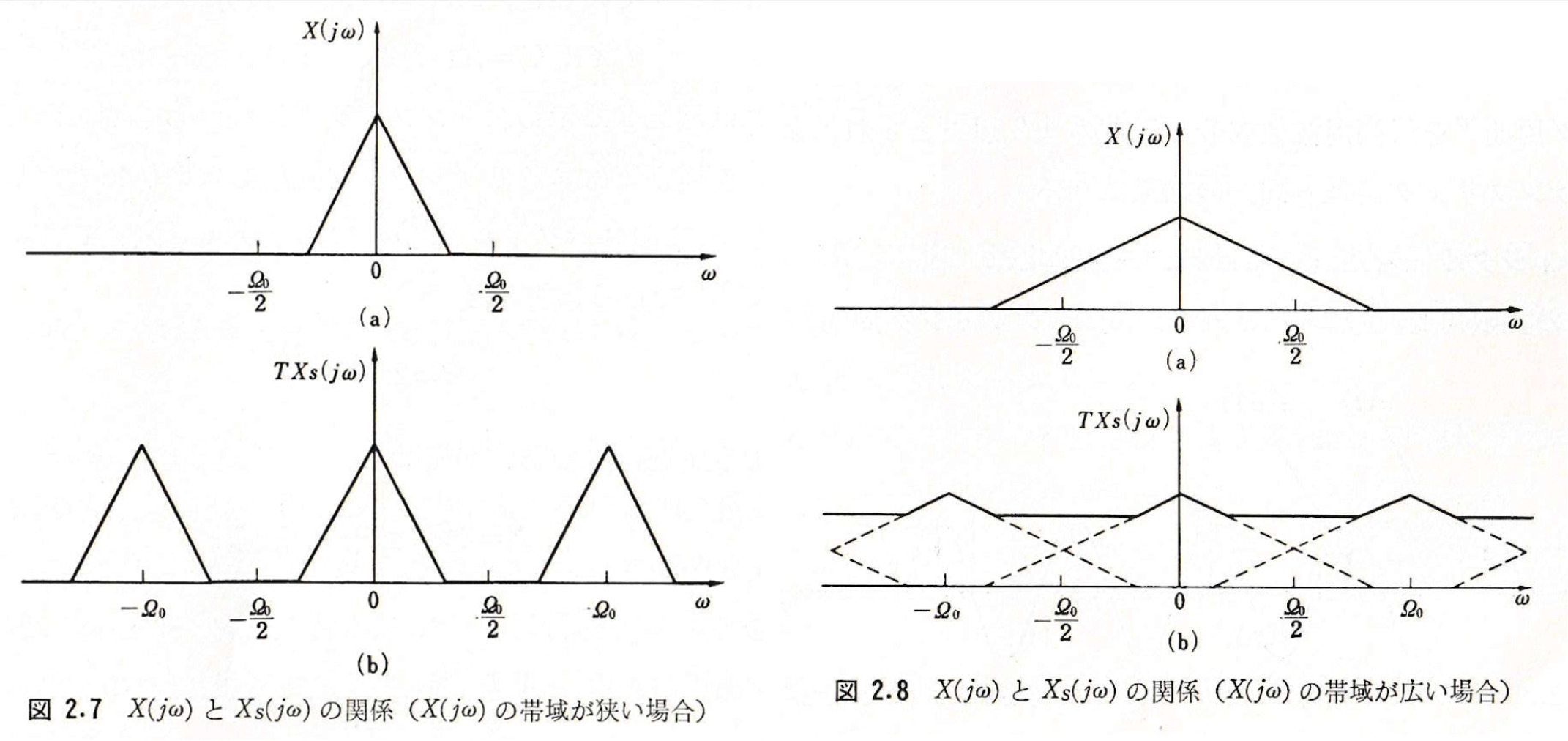
図 2.

このエイリアシングが発生するのを避けるためには,「サンプリング周期 $T$ を, 原信号 $x (t)$ の最高周波数成分の周期の半分以下に設定することが必要」である．

離散フーリエ変換

信号値系列 $x (n T)$ の時間表現信号を $x_{s} (t)$ とするとき, そのフーリエ変換 $X_{s} (j ω)$ は式 (5) に示したように次で与えられる：

\begin{matrix} (5′) & X_{s} (j ω) = \sum_{n = - \infty}^{\infty} x (n T) e^{- j ω n T} \end{matrix}

この

X_{s} (j ω)

の数値計算法を以下で示す．前述したように

X_{s} (j ω)

は

ω

に関して周期

Ω_{0} = 2 π / T

の周期関数であるから,

- Ω_{0} / 2

から

Ω_{0} / 2

までの範囲, 或いは,

0

から

Ω_{0}

までの範囲の

X_{s} (j ω)

を求めれば十分である．
我々が実際に観測できるのは, ある有限な範囲の信号値である．それを, 次としよう：

\begin{matrix} (13) & x (0), x (T), \dots, x ((N - 1) T) \end{matrix}

この範囲以外の信号値

x (n T)

は不明であるが, 簡単化のためにそれらは全てゼロと置くことにするか, または, 上記の信号値を周期

N

で繰り返す周期的な信号系列と見做してもよい．すると,

\begin{matrix} (14) & X_{s} (j ω) = \sum_{n = 0}^{N - 1} x (n T) e^{- j n ω T} \end{matrix}

となる．観測した信号の時間長は

N T

なので, 最も低い角周波数成分としては

\begin{matrix} (15) & ω_{0} = \frac{2 π}{N T} \end{matrix}

のものを計算することにし,

ω = k ω_{0} (k = 0, 1, 2, \dots, N - 1)

に於ける

X_{s} (j ω)

を求めることにすると,

\begin{aligned} X_{s} (k ω_{0}) & = \sum_{n = 0}^{N - 1} x (n T) \exp (- j n k \frac{2 π}{N T} T) \\ (16) & = \sum_{n = 0}^{N - 1} x (n T) \exp (- j \frac{2 π}{N} k n), k = 0, 1, 2, \dots, N - 1 \end{aligned}

となる．これは数値計算可能である．

k = N

に於いては,

ω = N ω_{0} = N \frac{2 π}{N T} = \frac{2 π}{T} = Ω_{0}

であるから,

ω = 0

から

ω = Ω_{0}

まで,

ω_{0}

の刻みで

X_{s} (j ω)

が定まることになる．式 (16) を信号値系列

{x (n T)}

の「離散フーリエ変換」(Discrete Fourier Transformation, DFT) という．次式が成り立つことは, 容易に確かめられる (前述のブログ記事を参照すべし)：

\begin{matrix} (17) & \frac{1}{N} \sum_{n = 0}^{N - 1} \exp (- j \frac{2 π}{N} k n) \exp (j \frac{2 π}{N} l n) = {\begin{cases} 1, & k - l が N の 整 数 倍 の と き \\ 0, & そ れ 以 外 の と き \end{cases} \end{matrix}

この関係を用いると,

\begin{matrix} (18) & x (n T) = \frac{1}{N} \sum_{k = 0}^{N - 1} X_{s} (k ω_{0}) \exp (j \frac{2 π}{N} k n), n = 0, 1, 2, \dots, N - 1 \end{matrix}

この式 (18) を「離散フーリエ逆変換」(Inverse Discrete Fourier Transformation, IDFT) という．

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31