様々な散乱現象 (Various Scattering Phenomena)
散乱現象を大きく分類すると, 弾性型と非弾性型とに分けることが出来る. 弾性散乱の場合, 重心系では二つの衝突粒子の運動エネルギーは一定に保存される.その代わり, どちらの衝突物体も励起状態にはならないし, 新たな粒子が生成されることもないと言える. 今考えている場合, 物体の一方は電子であるから, 核が実験室系で運動エネルギーを獲得する場合でも, 原子核は衝突前後で基底状態のままであることを観測すれば十分である. 非弾性散乱の場合では, 幾つかのタイプの振舞いを観測することが出来る. それらは後で列挙して述べることにする.
実際には, 核を取り巻く電場内には電子による沢山の軟放射量子(soft quanta) があるので, 散乱が正確に弾性的であるとは決して言えない.
例えば
(a) 核の反跳 (Nuclear Recoil)
様々な型の非弾性散乱を議論する前に, 実験室系では非弾性散乱のように見えるが, 実際には重心系で見られる弾性散乱であるような種類の散乱を考えてみよう.指摘しようとしているのは単に, 散乱電子から運動エネルギーと運動量が衝突された核に移行することで生じるエネルギー変化のことである.例えば, エネルギー
衝突の相対論的運動学は, コンプトン効果のそれに似ている.なぜなら, 散乱実験で用いられる高エネルギー (
は高い精度で次式で近似することが出来るからである:
これはX線の場合の関係式と同じである.コンプトン効果の衝突された電子の代わりに, この場合は衝突された核の質量を用いる.すると次の結果式を得る:
ただし
を計算する簡単で正確な方法である.高エネルギーの場合, この式は全く安心して用いることができる.誤差は
式(24)で角度
ただし,
そして,
そして
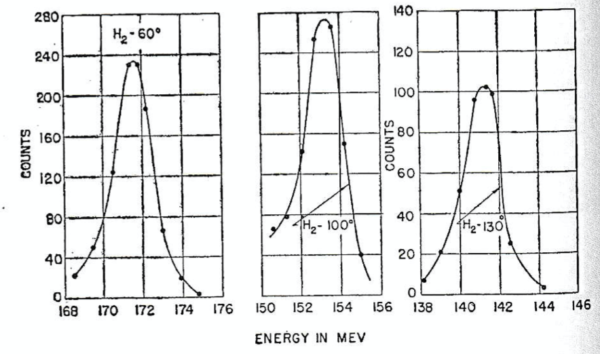
式(24)の実際の散乱問題への適用を説明する目的で図 9.を示しておく.この図は, 気体水素の標的に
式(24)の反跳エネルギーは標的核の質量数に反比例して変化する.従って, 複合標的中の2元素または同一元素の2つの同位元素では, 弾性散乱ピークの分離が可能となる.陽子からの電子散乱を研究して見ると, ポリエチレンは貴重な標的材料であることが分かる.なぜなら, 陽子の弾性散乱ピークは炭素の弾性散乱ピークからずっと離れた位置になり, 従って, バックグラウンド雑音の除去問題(background subtraction problem) は非常に簡単化するからである.この方法は有利ではあるが, しかし標的元素からの非弾性散乱のエネルギー位置が, 研究対象の元素または同位元素の弾性ピークと同じにならないことを心得ておく必要がある.
(b) 非弾性散乱 (Inelastic Scattering)
弾性散乱では, 散乱事象の前後で核は基底状態にあることが観測される.しかし非弾性的な変種では, 散乱事象が起こった後, 核は基底状態とは異なる状態になっている.すなわち, 通過する電子は, 核の基底状態をある励起状態への遷移, または連続準位中のあるエネルギー準位への遷移を引き起こす.以下のような可能性があるので述べて行くことにしよう.
(1) 核準位の励起 (Excitation of Nuclear Levels)
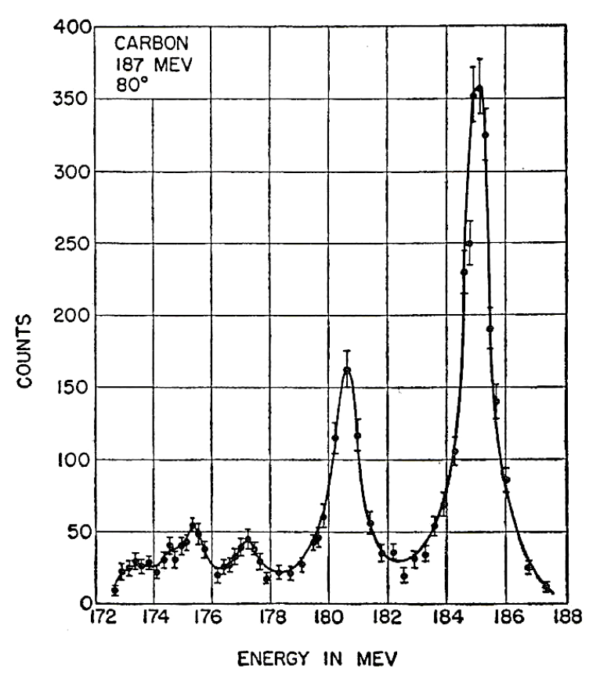
核は, 入射電子により離散的な励起状態に持ち上げられる可能性がある.そのとき電子は, 核が励起されたエネルギー分だけ失った状態で飛び去る.図 11. は, 炭素で観測されるこの現象を表したものであり, 入射エネルギーは
このタイプの非弾性散乱は, 非常に大きな本質的重要性を持っている.なぜなら, 核を調べながら, 核を高いエネルギー準位, 要するに他の方法ではほとんど到達することの出来ない高エネルギー準位に遷移させることが出来るからである.遷移行列要素や核の角運動量そして状態のパリティの値もやはり求めることが出来るであろう.定性的に言うならば, このタイプの非弾性散乱では核の動的特徴が明らかになるが, 弾性散乱では基底状態にある核の静的特徴が明らかになると言える.しかしながら, 実験的に言うならば, このタイプの非弾性散乱は, 弾性的ピークをその付近にある他のピークから分離しようとする時に幾つかの問題を引き起こす(pose).非弾性散乱とその解釈については, 後でまた述べることにする.
(2) 電磁崩壊 (Electrodisintegration)—原子核中の核子の運動量分布
第 2 の型の非弾性散乱は, 通過電子によって陽子か中性子が放出される時に起こる.この過程は「電磁崩壊」と呼ぶことが出来るであろう.この過程は重水素の場合に観測され, その次にヘリウムや他の元素でも確かめられた.図 12. では, ヘリウムのこの過程の非弾性的散乱の連続(continuum) が曲線の
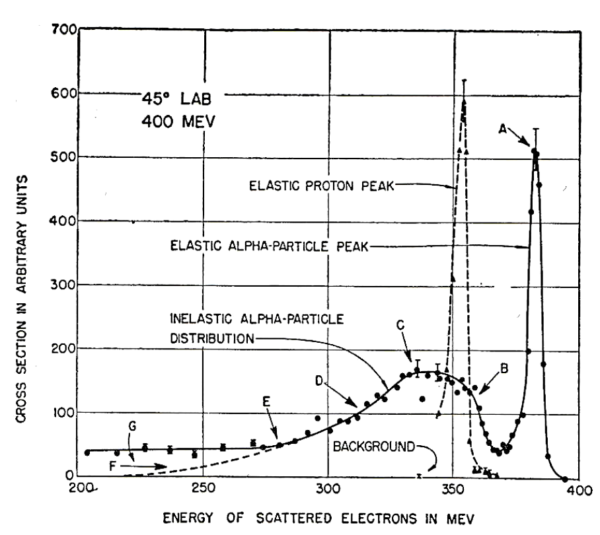
図 12.
弾性的ピークは位置
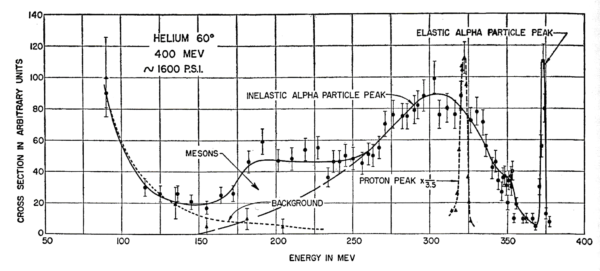
図 13. アルファ粒子から
「mesons」とラベル付けされている範囲は, 標的中で生成され, 相当する散乱電子と同じ運動量を持って出現する負のパイ中間子に関係する部分である.自由陽子ピークが比較のために示されている.
連続部分の低エネルギー側は, 自由陽子よりも, すなわち図 12. の自由陽子ピークの位置で与えられるエネルギーよりも高いエネルギーで, 陽子か中性子は放出され得るという事実に起因する(result from).もし核子が放出される前に(prior to ejection), 入射電子と反対方向の速度成分で運動しているならば, 放出された陽子や中性子は自由陽子の反跳よりもより少ないエネルギーを受け取ることも同様に起こり得るであろう.もし核子が入射電子の経路と平行な成分で運動しているならば, 反跳エネルギーはより大きくなるであろうし, 従って, 散乱電子はより少ないエネルギーを得るであろう.最後にもし核子が入射電子の経路に本質的に直交して運動しているならば, 散乱電子は, 自由陽子からの散乱電子と第1近似で一致するエネルギーを持つであろう.ただし上述した補正, すなわち核から核子を取り去るのに要するエネルギー, つまり束縛エネルギー分は除外する.図 12. の自由陽子ピークよりもおよそ
(3) 原子核の崩壊 (Breakup of the Nucleus)
(2)に類似しているが同時に一個以上の粒子が放出されるような過程も起こり得る. 重水素やアルファ粒子のような破片の放出が期待できる. ぼっとすると, より重い原子核の幾つかでは核分裂(fission) も起こるであろう. そのような核の崩壊は疑うことなく生起し, 図 12. に示されているような連続部分に寄与する. 核断片を特別に探す同定実験や分離実験(coincidence experiments or separate experiments) を実施することが出来ないならば, 単一核子の核崩壊過程と多重核子の核崩壊過程とを実験的に分離することは困難である.
(4) 中間子過程 (Mesonic Processes)
通過電子は, 様々なタイプの荷電中間子や中性中間子を核からまたは核子から放出させることが出来る. そのような粒子の質量エネルギー(materialization energy) が供給されなければならないのは勿論のことである. それは少なくとも
(5) 輻射 (Radiation)
電子の弾性散乱と非弾性散乱の両方で光子の放射が付随する. 放射が主に前方に向かう場合, この放射は馴染みのあるベータトロンやシンクロトロンで観測される
上述の見解(foregoing remarks) は実量子の放出についての言及である. 散乱作用の間には仮想放射の放出と吸収も生起することはよく知られたことである.実の放射のみならずこの過程も含んだ計算は Schwinger によって, そして後に Suura によって為された. Suura は Schwinger の計算により一般的な立証を与えた. 目的がより実用的である場合には, 散乱実験は補正が必要であって,
ただし
ただし,
そして式中の
有限な厚さの衝突源より現れる電子に依る実放射の放出すなわち制動放射(bremsstrahlung) もやはり補正が必要である. その結果は次のようなものとなる:
ただし
そして
(c) 磁気散乱 (Magnetic Scattering)
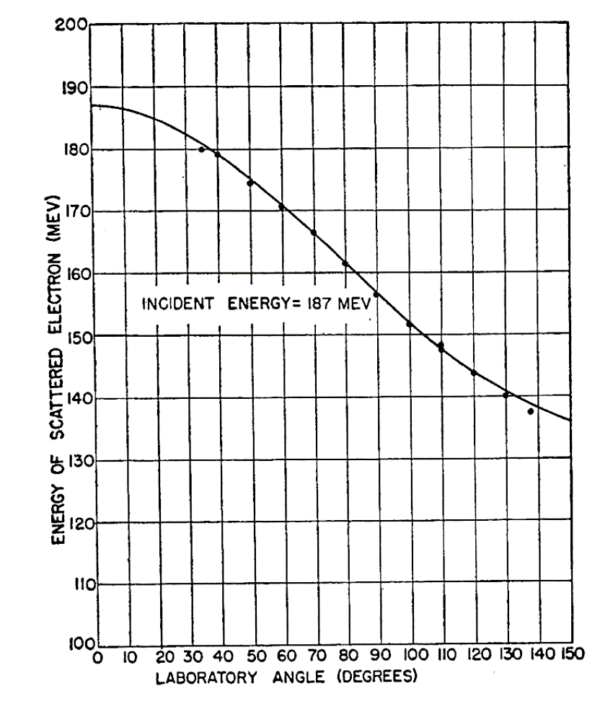
多くの原子核の弾性散乱は全て核子の電荷, すなわち核を取り囲む電場が原因である.しかしながら有限な大きさの影響により, 高エネルギーでの大角度の弾性散乱は, 点電荷とクーロン相互作用から予想される散乱よりも数桁小さくなる(by many orders of magnitude below) 可能性がある. 次のように問うて見よう:「電荷散乱が実験的に認識されなくなった後, 何らかの弾性散乱が残っているであろうか?」(Does any elastic scattering remain at all after the charge scattering has dropped below experimental recognition?). 関連する別の質問は「中性子は高エネルギーで電子を散乱させるであろうか?, そして原子核内の中性子は電子を散乱させるであろうか?」. 全ての場合で答えはイエスであり, スタンフォード大学の実験で磁気的散乱は実際に観測されている.
「陽子(The proton)」— 陽子の磁気モーメントによる高エネルギー電子の弾性散乱は, 実は1950年に Rosenbluth によって予言されていた. Rosenbluth は, 陽子の Dirac 磁気モーメント成分と Pauli 磁気モーメント成分の両方が弾性散乱に寄与することを示した. Pauli モーメントは大抵は陽子磁気モーメントの「異常部分」(anomalous part) と呼ばれている.
ディラック理論によると, スピン
陽子が同様に内部構造を持たない粒子であれば, 陽子の磁気モーメントは核磁子(nuclear magneton) の値
Rosenbluth が示した結果は, 以下のように表現することが出来るであろう : 陽子的な点電荷と点磁気モーメントの場合, 微分断面積
ただし,
そして,
式(36)は
最後に, 式(35)は磁気的散乱を考慮した次の因子
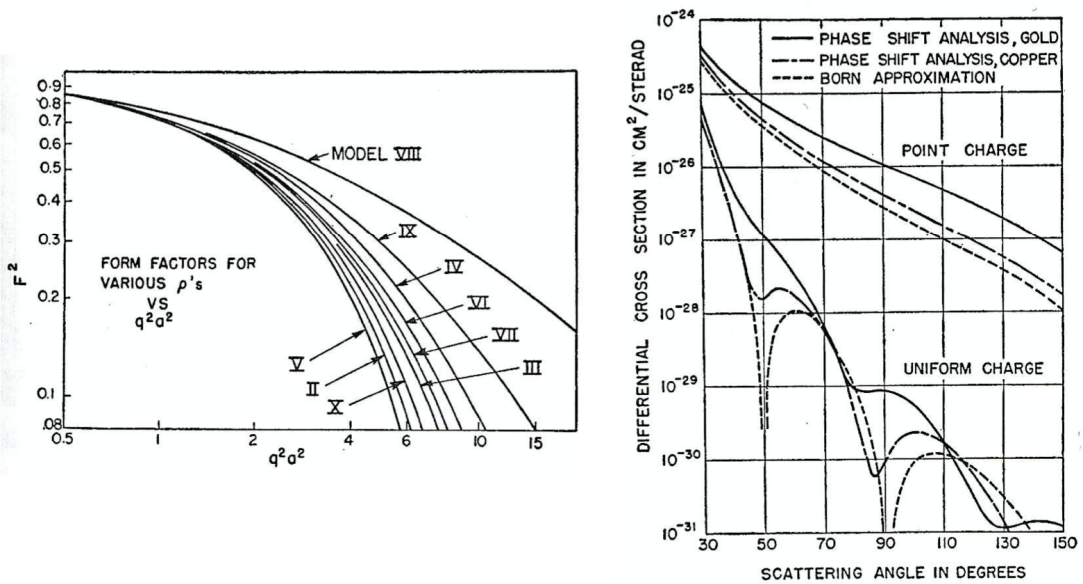
さて次に, もし陽子がたまたま(中間子理論で期待されるように) 点電荷でも点磁気モーメントでもないとしたら, その場合には形状因子の存在が要請される.これが存在すると電荷と磁気モーメントの有効値が減少することになる. 実際, Rosenbluth は弱結合の中間子理論を用いてそのような計算を行った. しかし, 現今では申し分のない中間子理論の存在が知られていないので, 陽子が有限な大きさを持つことによる効果を考慮する(allow for) には, 現象論的な形状因子を用いるのが好ましい. 陽子の「大きさ」とその「形」は, 陽子が放出し再吸収できる荷電中間子及び中性中間子の仮想雲が持っているとする. 現象論的な形状因子
「中性子 (The neutron)」—中性子の場合はその電荷がゼロなので, 素朴な試みは
上記で議論された概念の重要なレビューは, 参考文献57に示した Yennie 等のものである. ここでは更なる考察として次を指摘して置くだけにしておく : 電気力学の破綻(breakdown), 例えば近距離でのクーロン則の破綻(failure)は, 有限サイズになると全く同じ影響を受けるであろう. この点については後で(第7章で) また考えるつもりである.
「重陽子 (The deuteron)」—重陽子からの磁気散乱の場合, 期待される断面積は陽子のそれよりも小さいはずである. なぜなら, 重陽子の静磁気モーメントは
面積は磁気モーメントの2乗の関数として変化するので, 重陽子の磁気散乱は陽子のそれに比べおよそ
ただし
当然のことだが, もし磁気モーメント
または,
これらの式で
他のスピンを持った原子核たち(nuclei)も適切な条件下では弾性的な磁気的散乱を示すことは明らかである. しかしながら, 磁気的散乱が重要となるのはゼロでないスピンの軽い元素, 例えば Li など, の場合だけであると予想される. 重いか中間的な重さの元素では, 磁気モーメントとスピンは沢山の粒子中に僅かに存在する不対粒子たちだけに起因し, それ以外は電荷を担っている. 磁気的効果は表面に存在しており, そして恐らくは電荷散乱の形状因子よりもさらに速く減少する形状因子を伴っているであろう.
(d) 原子核の角度的形状 (Angular Shapes of Nuclei)
今まで議論してきたのは, 動径方向電荷密度の変動のみであり, その中で原子核の大きさが有限であることの影響を考慮していた. しかし実際には, 原子核の4重極モーメントに関するスペクトル分析やその他の事実の論文が, 魔法数の原子核(殻クロージャ)の仲間の核たちは歪んでいて球状ではないことを示唆している.
魔法数の近くにある原子核はほとんど間違いなくほぼ球形である. アルファ粒子と陽子によるクーロン励起の最近の数年の実験では, 「多くの原子核が基底状態では楕円形であること」をより一層確信させるようなデータが得られている. ボーア-モッテルソン模型によるこの形の説明は, 「核子たちが一緒になった集団運動が原子核表面上を運動する膨らみ(bulge) を生成するからである」としている. そのような運動は「回転的準位」と呼ばれる低エネルギー準位に相当している. そう呼ばれるのは, 分子の回転状態との類似性のためである. そのような原子核, 例えば希土類元素である Ta, W, U などが実際にどのような形であろうと, それらには特別な何かがあるのはほとんど疑う余地がない. これらの原子核の特殊性は電子散乱の研究に於いても提示されている. それらの研究によると,Pb
実験曲線を解釈する際には, 楕円形状の影響を含め, そして近づいて来る電子たちが受けるその影響をあらゆる角度から適切に平均化する必要がある. この平均化は, 原子核表面を丸くしそして見かけの表面を実際よりも不明瞭(厚いthicker?) にする効果を持つ. しかしながら, 主に核表面はすでに不明瞭であるために, この平均化による核表面の球状化は散乱に大きな変化を与えることはない. ともかく, それは散乱が平らになるという特徴を説明するには十分ではない. 低エネルギー準位が存在するということは, それらの状態に散乱する影響も考慮に入れなければならないということを意味している. すなわち, 電子散乱にはこれらの準位への遷移も含まれるということである. 基底状態から回転的励起状態への一方的な遷移は非弾性散乱を引き起こす(原因となる:give rise to). しかしながら, 基底状態と回転的状態のエネルギー間隔は小さいので, 散乱実験で得られている現時点の解像度を考えると, そのような非弾性散乱は隠れてしまって検出されないであろう. 静的散乱から回転的散乱を分離するのには, 2000分の1の分解能が必要であろう.
散乱に対する四重極モーメントの影響の理論的取り扱いは, タンタル近辺の原子核たち(for the nuclei in the region of Tantalum) について, Schiff また Downs, Ravenhall, Yennie によって与えられた.この研究の議論は, 実験的結果を議論した後でもう一度行うであろう.
(2) R.W.McAllister and R.Hofstader, Phys. Rev. 102, 851 (1956).
(3) McIntyre, Hahn, and Hofstader, Phys. Rev. 94, 1084 (1954).
(4) L.I.Schiff, Phys. Rev. 96, 765 (1954).
(5) R.Blankenbecler and R.Hofstader, Bull. Am. Phys. Soc. Ser. II,1,10 (1956).
(6) Blankenbecler,Hofstader, and Yearian (unpublished).
(7) S.J.Biel and E.H.S. Burhop, Proc. Phys. Soc. (London) A68, 165 (1955).
(8) J.Schwinger, Phys,Rev. 75, 898 (1949).
(9) H.Suura, Phys,Rev. 99, 1020 (1955).
(10) H.A.Bethe and J.Asjkin, Experimental Nuclear Physics, edited by E.Segé (John Wiley and Sons, Inc., New York, 1953), Vol.I, Part II, p. 272. This result is derived from the original Bethe-Heitler theory.
(11) R.Hofstadter and R. W. McAllister, Phys. Rev. 98, 217 (1955).
(12) M.N.Rosenbluth, Phys. Rev. 79, 615 (1950). See also the reference to L.I.Schiff in this paper.
(13) Yennie, Lévy and Ravenhall (to be published).
(14) L.L.Foldy,Phys. Rev. 87, 688 (1952); 87, 693 (1952).
(15) V.Z.Jankus, Phys. Rev., to be published.
(16) A.Bohr and B.R.Mottelson, Kgl. Danske Videnskab. Selskab. Mat.-fys. Medd. 27, No. 16 (1953).
(17) Downs, Ravenhall, and Yennie (to be published).