ROBERT HOFSTADTER の論文 part 1

ファインマン&ヒッブスの【問題 6-9】は, 電子散乱実験により核半径及び核電荷密度を求めるための条件について考察する問題であった．実は, この電子散乱による原子核研究は1950年代に加速器によって盛んに行われたようである．その成果すなわち「加速器による高エネルギー電子散乱の研究と核子の構造に関する発見」によって R.Hofstadter は1961年にノーベル賞を受賞している．そこで参考のために, ホフスタッターが書いた論文の一つを訳出しておこう．ただし原文は長いので第4節以降は省略し, また2回に分けて示すことにする．多少は自己流の補足情報も挿入してある．また, 脚注を記事に付ける仕方がまだ分からないので, 主な脚注も補足情報として示した．理論や実験の予備知識として, (誤訳も多分あると思うので) 批判的に読んでみて欲しい．

Electron Scattering and Nuclear Structure
1. 導入
2. 散乱理論

Electron Scattering and Nuclear Structure

ROBERT HOFSTADTER

導入

数年前まで, 核構造の幾何学的な詳細に関する主要な情報は, 鏡映核 (mirror nucleus) のエネルギー放出比較, 高速中性子捕獲の散乱断面積(及び全断面積)，Weiszacker の半経験的公式と関わりのある束縛エネルギー, そして重元素の場合のアルファ崩壊のエネルギーと半減期, の実験から導き出されていた．核の適切なモデルとして普遍的に受け入れられている「一様に荷電した球」とした場合の核半径の値は, 全ての方法でだいたい同じ範囲となった．その結果は, 一様球とした場合の核半径に対するよく知られた次の式に要約される：

\begin{matrix} (1) & R = r_{0} A^{1 / 3} \times 10^{- 13} cm = r_{0} A^{1 / 3} fermi, \to R_{Au} = 1.45 \times \sqrt[3]{197} \approx 8.44 fermi \end{matrix}

(ただし

A

は原子核の質量数である)．今後は, 全ての距離を

10^{- 13}

cm を単位とした表現で測定することにする．この単位を「fermi」と呼ぶことにする．

(1)「鏡映核」とは, ある原子核の中性子を陽子に,陽子を中性子に変えて得られる原子核のことを言う．M.Born：「現代物理学」§7.1には,「鏡映核」を考えることで核半径を見積もる方法や, アルファ崩壊による核半径の考察が述べられている．
(2) B.ポッフ他：「素粒子・原子核物理入門」の § 2.1 には「ヴァイツゼッカーの質量公式」の分かり易い説明がある．
(3) 核物理学では便利な単位であるため, 1964年にSI接頭辞フェムトが制定される前から, 同じ長さに独自の名前をつけた単位が使われていた．フェルミ (fermi) はエンリコ・フェルミにちなんだ単位で, 1956年, ロバート・ホフスタッターが Reviews of Modern Physics 誌で導入した(すなわちこの論文である)．なお, フェルミの単位記号の1つ fm はフェムトメートルの単位記号と同じである．ユカワ (yukawa) は湯川秀樹にちなんでいる．いずれもSIには採用されず, 現在ではフェムトメートル (fm) を使う．

1

fm =

0.001

pm =

10^{- 15}

mである．(Wikipedia より)．

例えば， $r_{0}$ として $1.45$ fermi 近くの妥協値を与えた場合, この公式は金の原子核の端が中心から $8.44$ fermi の距離だとする．このモデルは全ての原子核に一様な質量密度を与える．すなわち, 金の質量数は $A = 197$ であるから,

\begin{aligned} ρ_{M} & = \frac{A}{\frac{4}{3} π R^{3}} \frac{nucleons}{(fermi)^{2}} = \frac{1}{\frac{4}{3} π r_{0}^{3}} \frac{nucleons}{(fermi)^{2}} \\ (2) & = 0.078 \frac{nucleons}{(fermi)^{2}} \end{aligned}

そして, 原子核の種類によって変化する電荷密度は式(1)より

R^{3} = A r_{0}^{3}

なので次となる：

\begin{aligned} (3) & ρ_{C} & = \frac{Z e}{\frac{4}{3} π R^{3}} = \frac{Z e}{A \frac{4}{3} π r_{0}^{3}} = \frac{Z}{A} \times 0.078 \frac{proton charges}{(fermi)^{2}} \end{aligned}

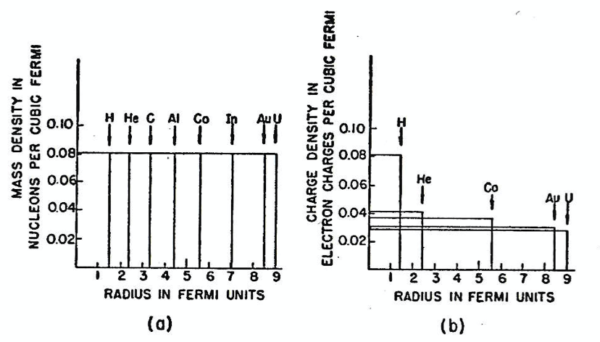
図1 の (a) と (b) には, これらの式が描かれており, 幾つかの代表的な原子核の相対的な大きさと形が示されている．

図 1. (a) 原子核を一様球とした場合の核の質量密度 $ρ_{M}$ ．(b) 一様球モデルでの核電荷密度 $ρ_{C}$ ．

ここ数年の Lyman 他, Hofstadter 他, Pidd 他, そして Fitch と Rainwater 他の電子散乱とミュー中間子的原子の研究によると, 重元素の場合, これらの実験法によって決定される原子核半径は, 式(1)で $r_{0} = 1.45$ fermi としたときに比べ約 $20$ % ほど小さな値となることが示された．より軽い元素に於いても, より小さい半径： $r_{0} = 1.20$ fermi を持つことを同じ公式から $μ$ -中間子の結果で示された．同じ時期に Cooper と Henley は, ミラー原子核のデータ, それは勿論軽い原子核に関係したものである, は半径がより小さいとすれば説明し得ることを提起した．その後, この結論について幾分かの疑問が表明された．事情がどうであろうと, これらの方法で得られたより小さな半径は「電磁気学的半径」(electromagnetic radii) と呼ばれるようになった．より良い呼称を求めるならば， $r_{0} = 1.45$ fermiのときに式(1)で与えられる半径は「原子核工学的半径」(nucleonic radii) と呼べるかも知れない．なぜなら, より大きな値は核粒子たち(nucleons) が原子核たち(nuclei) と相互作用する実験で得られたからである．
1953-1956年の期間にスタンフォード大学で, 電子散乱についてかなりの量の研究が行われた．この研究により, 陽子からウラニウムの範囲に及ぶ原子核の電荷密度についての情報がもたらされた．この題材を扱う状況レポートのようなものを書くのは時宣を得たことであるように思われた．そのようなレポートは様々な既存情報を一緒にする効果を持ち得るであろうから,「電子散乱」による半径と電荷分布の値を, より一般的な分野で核半径を研究する人たちが自分のデータと比較することが出来るのではなかろうか．このレビューの目的は, まだ発表されていない幾つかの研究も含んだそのようなデータ編成を提示することである．このレポートは電子散乱法で決定された核の大きさと形の最終報告と見做されるべきではない．事実はそれどころか(indeed), 今後の高エネルギーでの電子散乱実験計画では, 疑うことなく現在とは違う結論や, ひょっとすると予期しない結論も出されるであろう．しかしながら, 重大な相違が生じることは恐らく無いと思われる．従って, この時点でのレポートは適切かも知れない．このレポートは, 電子散乱研究に従事している他の実験所の研究の歴史的レポートを意図していないし, 総括レポートを意図したものでもない．この分野や他分野の研究者が核半径データを収集することを奨励する刺激として機能することを切に願うところである．Ford と Hill による核電荷分布のレビューが最近発表されたが, それはこの意味での一つの前進である．

散乱理論

(a) 点電荷からの散乱

荷電粒子が関係する弾性散乱の全ての根元にあるのはラザフォードの有名な公式である．その公式,

\begin{matrix} (4) & σ (θ) = \frac{Z^{2} z^{2} e^{4}}{16 E^{2}} \frac{1}{\sin^{4} \frac{θ}{2}} \end{matrix}

は, 例えば (電荷

Z e

で帯電した) 重い原子核のような電場の強い源と見做せる, 不動の点電荷中心に対して, 運動エネルギー

E

を持って入射する (電荷

z e

で帯電した) 荷電点粒子散乱の微分断面積

σ (θ)

を表現している．ただし

θ

は散乱の天頂角(polar angle) である．式(4)のラザフォード散乱は, 古典力学でだけでなく量子力学に於いても正しいことが示されている．
ラザフォード散乱則は中位のエネルギーを持ったアルファ粒子や陽子には適合するけれども, それは相対論的な公式ではないので, 散乱相手のスピン可能性もスピン同一性も考慮した式ではない．
点状原子核に対する, 例えば電子のようなディラック粒子の相対論的散乱は Mott の有名な論文に於いて熟考された．その場合, 入射粒子である電子はスピン (そしてデイラックの磁気モーメント) を持っていると仮定するが, 散乱中心である原子核はスピンも磁気モーメントも持っていないと仮定する．
Mott は, 弾性散乱断面積の級数展開について議論展開し, また次の不等式

\begin{matrix} (5) & \frac{Z}{137} = Z \frac{e^{2}}{ℏ c} ≪ 1 \end{matrix}

を満たす元素(elements) の場合に導出される近似式も提示した．
Mott の近似は「モット散乱」と呼ばれ, 次の式(6)で与えられる：

\begin{matrix} (6) & σ_{M} (θ) = {(\frac{Z e^{2}}{2 m c^{2}})}^{2} (\frac{1 - β^{2}}{β^{4}}) \frac{1}{\sin^{4} \frac{1}{2} θ} (1 - β^{2} \sin^{2} \frac{1}{2} θ), \end{matrix}

ただし，

v

と

c

は各々入射粒子と光の速度である：

\begin{matrix} (7) & β = \frac{v}{c}, z = 1; \end{matrix}

m

は電子の静止質量である．式(6)は質量中心座標の表現で書かれている．このような観点で記述されるような条件下では

β

は1に非常に近いのが常であり, そのため式(6)では

β^{4}

は1に等しいとされる．従って, 次式が高精度で成り立つ：

\begin{matrix} (8) & 1 - β^{2} \sin^{2} \frac{1}{2} θ \approx 1 - \sin^{2} \frac{1}{2} θ = \cos^{2} \frac{1}{2} θ \end{matrix}

更に, 電子の全エネルギーは次であった：

\begin{matrix} (9) & E = \frac{m c^{2}}{\sqrt{1 - β^{2}}} \end{matrix}

従って,

\begin{matrix} (10) & 1 - β^{2} = {(\frac{m c^{2}}{E})}^{2} \end{matrix}

これらの変更を式(6)に施すと, 電荷

Z e

のスピンを持たない点状原子核に対するスピンを持つ電子の弾性散乱についての Mott の相対論的公式となる：

\begin{matrix} (11) & σ_{M} (θ) \approx {(\frac{Z e^{2}}{2 m c^{2}} \cdot \frac{m c^{2}}{E})}^{2} \frac{1}{\sin^{4} \frac{1}{2} θ} \cdot \cos^{2} \frac{1}{2} θ = {(\frac{Z e^{2}}{2 E})}^{2} \frac{\cos^{2} \frac{1}{2} θ}{\sin^{4} \frac{1}{2} θ} \end{matrix}

この公式は全くもって非常に簡単な形をしている．

座標が実験室系の場合には, 後で示される式(36)のように修正する必要があることに注意する．

条件式(5)が満たされるときに, 式(11)は極めて正確である．しかしながら, 大きな $Z$ を持つもっと重い原子核の場合, 予想されることではあるが, 式(11)は間違ったものとなることが示された．多くの研究者によって式(11)の改良が試みられたが, それらの計算の詳細はここでは示さない．McKinley と Feshbach, そして Feshbach が様々な研究を総括し, 彼ら自身も大きな $Z$ 値を持つ原子核に対する式(11)の適切な修正を提出している(put forward)．それらの研究は，Dalitz がボルンの第2近似を用いることで立証された．
$Z / 137$ が大きくない場合には, 条件(5)を緩和する以外は式(11)と同じ条件下で, 式(11)のより良い近似式が上記の著者たちによって与えられた：

\begin{matrix} (12) & σ_{F} (θ) = {(\frac{Z e^{2}}{2 E})}^{2} \frac{\cos^{2} \frac{1}{2} θ}{\sin^{4} \frac{1}{2} θ} [1 + \frac{π Z}{137} \frac{(\sin \frac{1}{2} θ) (1 - \sin \frac{1}{2} θ)}{\cos^{2} \frac{1}{2} θ}] \end{matrix}

小さな角度では, 式(11)と式(12)とは互いに等価である．大きな角度に於いても, 誤差は比較的小さい (角度

θ

が

0 \sim 90

°まで変化しても角カッコ内の角度因子部分の変化は約

0 \sim 0.5

に過ぎない)．式(11)の代わりに式(12)を用いたときの相対誤差は

θ = 90

°では Si で3%，Ze で7%, また

θ = 135

°では Si で17%，Ze で35%である．式(12)は重い原子核には用いることが出来ない．全ての

Z

値に対する式(12)に類似した閉じた公式(closed formula) は与えることが不可能である．しかし大きな

Z

での散乱の数値的評価式は Feshbach の論文に与えられている．この著者は陽電子の散乱結果に相当する式も与えている．Bartlett と Watson は重い原子核である水銀 (

Z = 80

) の正確な数値計算を行った．式(11)と式(12)で与えられる角度分布は, 入射エネルギーに依存していないことに気付くであろう．しかし, これらの式は無限に重い原子核からの散乱に適用されるもので, 従って厳密に適用できるのは座標が重心系の場合だけであることを忘れてはならない．もっと現実的に従来の質量値で原子核を考える場合, 入射電子が 100MeV 以上のエネルギーを持つ場合の重心はかなりの速度で前進するので, 高エネルギー時のこの効果のため, 角度分布は前方にピークが存在するであろう．この問題は後で再び言及するであろう (III-cを見よ)．
銅および金の点電荷による高エネルギー電子の弾性散乱について正確な計算を Yennie, Ravenhall, そして Wilson は位相変位法(phase-shift methods) を用いて行ない, これに相当する第1ボルン近似とそれとを比較した (参考文献9の図1)．

(b) 有限な大きさを持った原子核からの散乱

原子核が有限なサイズを持つとした場合の電子散乱への影響を最初に考察したのは Guth である．それとは独立的に, 似た考えが Rose によって展開された．より正確な方法を用いることで，Elton，Feshbach，Achesonは, 低エネルギー( $20$ MeVまで) の電子散乱実験に関係する有限サイズ問題を考察した．他方，Parzen は鉛について $100$ MeV のエネルギーの場合を論じた(deal with)．更にその後，Smith はこの問題を, 高エネルギー電子での問題として第1ボルン近似を用いて詳細な研究を行ない, 続いて彼は主要な結果を簡潔な形で提示した．
Smith の結果は( $Z$ が小さい)軽い原子核に正確に適用できるだけでなく, 彼の結果の幾つかは弾性散乱及び非弾性散乱の両方にも言及している．Schiff は, 同様な第1ボルン近似計算を高エネルギーに於いて行ない, その論文中では他の興味ある物質の計算も行った．
第1ボルン近似は, 軽い元素には支障なく適用できる．また, この近似では核サイズを有限とした場合の質的効果を容易に評価できる．よって, 次の数節はこの話題に費やすことにしよう．

(4) W.A.McKinley,Jr., and H.Feshbach, Phys. Rev. 74, 1759 (1948). [この著者たちは上記の式(12)がJ.Schwingerによっても導出されたことを指摘している]．
(5) H.Feshbach, Phys. Rev. \textbf{88}, 295 (1952).
(6) R.H.Dalitz, Proc. Roy. Soc. (London) A206, 509 (1951). [ G.Parzen and T.Wainright, Phys. Rev. 96, 188 (1954)も参照のこと]．
(7) E.Guth, Wiener Anz. Akad. Wiss. No. 24, 299 (1934).
(8) J.H.Barlett and R.E.Watson, Proc. Am. Acad. Arts Sci. 74, 53 (1940).
(9) Yennie, Ravenhall, and Wilson, Phys. Rev. 92, 1325 (1953).
(10) Yennie, Ravenhall, and Wilson, Phys. Rev. 95, 500 (1954).
(11) M.E.Rose, Phys. Rev. 73, 279 (1948).
(12) L.R.B.Elton, Proc. Phys. Soc. (London) A63, 1115 (1950); 65, 481 (1952); Phys. Rev. 79, 412 (1950)．
(13) H.Feshbach, Phys. Rev. 84, 1206 (1951)．
(14) L.K. Acheson, Phys. Rev. 82, 488 (1951).
(15) G.Parzen, Phys. Rev. 80, 261 (1950); 80, 355 (1950). [後者には数値的な誤りがあり,散乱曲線(論文の図1)は正しくない．]
(16) J.H.Smith, PhD., thesis, Cornell University, February, 1951 (unpublished).
(17) J.H.Smith, Phys. Rev. 95, 271 (1954).
(18) L.I.Schiff, Phys. Rev. 92, 988 (1953).

(1) 第1ボルン近似

Rose, Smith などは, 点電荷の場合の式(11)に対応して,「核が有限の場合」では, 式(11)と置き換わる弾性散乱の散乱公式は次の形をしていなければならないことを示した：

\begin{matrix} (13) & σ_{S} (θ) = {(\frac{Z e^{2}}{2 E})}^{2} \frac{\cos^{2} \frac{1}{2} θ}{\sin^{4} \frac{1}{2} θ} {| \int_{\begin{matrix} nuclear \\ volume \end{matrix}} ρ (r) e^{i k \cdot r} d^{3} r |}^{2} \end{matrix}

ただし

ρ (r)

は核内の電荷密度で核の重心からの動径ベクトル(radius vector) の関数である．また

q = ℏ k

は運動量移行である．従って, 図 2 のように

p_{0}

と

p_{1}

が入射運動量と散乱運動量で

| p | = | p_{1} | = | p_{0} |

であるとき, 弾性散乱の場合の

q

の数値的な大きさは次で与えられる：

\begin{matrix} (14) & q = 2 | p | \sin \frac{θ}{2} = 2 \frac{h}{λ} \sin \frac{θ}{2} \approx \frac{2 E}{c} \sin \frac{θ}{2} \end{matrix}

式(14)の

λ / 2 π

は高エネルギー

E

を持つ入射電子の換算 de Broglie 波長であり, 電子の静止質量

m c^{2}

を無視する近似をするならば次のように表せる：

\begin{matrix} (15) & \frac{λ}{2 π} = \frac{ℏ}{p_{0}} = \frac{1}{k} \approx \frac{ℏ}{E / c} = \frac{ℏ c}{E} = \frac{ℏ}{\sqrt{2 m E}}, (E \approx m c^{2} + \frac{p_{0}^{2}}{2 m} \to p_{0} = \sqrt{2 m E}) \end{matrix}

従って, 式(13)の

k \cdot r

は無次元の位相因子である．再び「原子核は反跳しない, または等価的に言えば, 図2は重心系で書かれている」と仮定する．

重心系では, 衝突前後で2粒子の速度は変化しない．例えば野上：「力学演習」の§5.3を見よ．

従って, 重心系では, 最初に原子核が静止しているならば衝突後でもやはり静止している(反跳しない)ことになる．
式(13)中の積分は簡単化可能であることが証明できる．従って,

\begin{matrix} (16) & σ_{S} (θ) = {(\frac{Z e^{2}}{2 E})}^{2} \frac{\cos^{2} \frac{1}{2} θ}{\sin^{4} \frac{1}{2} θ} {[\int_{0}^{\infty} ρ (r) \frac{\sin q r / ℏ}{q r / ℏ} 4 π r^{2} d r]}^{2} \end{matrix}

この式は角カッコ中の量が式(11)で与えられている点電荷の断面積に掛け合わされている．この式に類似した電子散乱及び X-線散乱で確立されている前例に従うのが慣例である．そこで, この量は「形状因子」(form factor) または「構造因子」(structure factor)と呼ばれ, これは有限な核電荷分布に相当するものである：

\begin{matrix} (17) & F = \int ρ (r) e^{i k \cdot r} d^{3} r = \int ρ (r) e^{i q \cdot r / ℏ} d^{3} r = 4 π \int_{0}^{\infty} ρ (r) \frac{\sin (q r / ℏ)}{q r / ℏ} r^{2} d r \end{matrix}

図 2．電子散乱に於ける運動量移行 $q$ ．重心系に於ける弾性散乱では $| p_{1} | = | p_{0} |$ である．
　図 3. 典型的な電荷分布についての形状因子 $F$ の2乗の様子

実際, 類似性は非常に近く, 原子の電子雲を核の陽子雲で置き換えることが必要なだけである．式(16)の電荷密度が1に規格化されているならば, 形状因子 $F$ は無次元量である．
第1ボルン近似を扱うとき, 中心となる考えは以下である：「有限な大きさの核からの本当の散乱を得るのに必要なのは, 考えている核の特定なモデルにふさわしい形状因子の2乗を点電荷の散乱断面積に掛け合わせるだけである」．この手続きは計算が非常に直接的で, 通常では非常に簡単である．というのは, 必要なのは一つの求積積分(quadrature) を[式(17)を]評価することだけだからである．軽い原子核の場合, これは申し分のないものである．残念ながら, 中間的な核や重い核の場合では, この手続きは役に立たない(fail)．よく知られているように, 第1ボルン近似は入射波と反射波の両方を平面波として考えることと等価である．実際では, それらの波は核の強い電磁場で歪められる．従って, それらはもはや平面波とは見做されない．おそらくは, このことを次のように言っても同じことであろう：第1ボルン近似は力場内の単一散乱になるが, 厳密な散乱は同じ力場での複数散乱によって決まる(depend on a plurality of scatterings)．
いかなる場合でも, 弾性散乱にボルン形式を適用することは軽い核による電子散乱を分析する際の非常に有益な手段であり, そして重い核を議論する際にも定性的価値を持つ手段である．後で, 第1ボルン近似の正確性について更なる言及を行うつもりである．
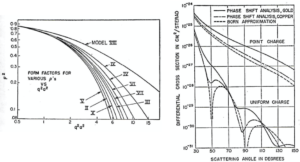
では, 式(17)を利用して幾つかの有用な原子核モデルの結果を示すことにしよう．計算を最も簡潔な仕方で提示するために, 表 I に幾つかの核電荷密度分布に対する形状因子を用意した(この表の便利な形式はE.E.Chambersに拠るものである)．表中の “ $a$ ” は, 電荷に応じて重み付けられた2乗平均根半径(r.m.s. radius) を表しており, その定義は次である：

\begin{matrix} (18) & a = \int_{0}^{\infty} ρ r^{2} 4 π r^{2} d r = 4 π \int_{0}^{\infty} ρ r^{4} d r \end{matrix}

ただしこのとき, 電荷密度

ρ

は1に規格化されている：

\int_{0}^{\infty} ρ 4 π r^{2} d r = 1

y

は比

y = r / a

であり, これは r.m.s.で表した半径距離尺度である．表 I 中の

x

の定義は

x = q a / ℏ

である．
もし

q a / ℏ

が小さい(ただし

a

は2乗平均根半径)と, 全ての形状因子は簡単な展開式になる：

\begin{matrix} (19) & F = 1 - \frac{1}{6} \frac{q^{2} a^{2}}{ℏ^{2}} + \dots \end{matrix}

高エネルギーでは高次の項が必要となるので, この近似は役に立たない．(

q a

が大きくなるので, 微小量での級数展開という仮定が成り立たなくなるからである)．

表 I． $ρ (r)$ は電荷密度関数である． $a$ は電荷分布の2乗平均根半径である． $F (q a)$ は形状因子である． $x = q a$ である．

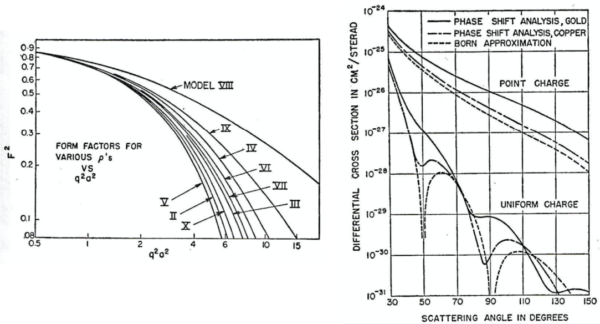
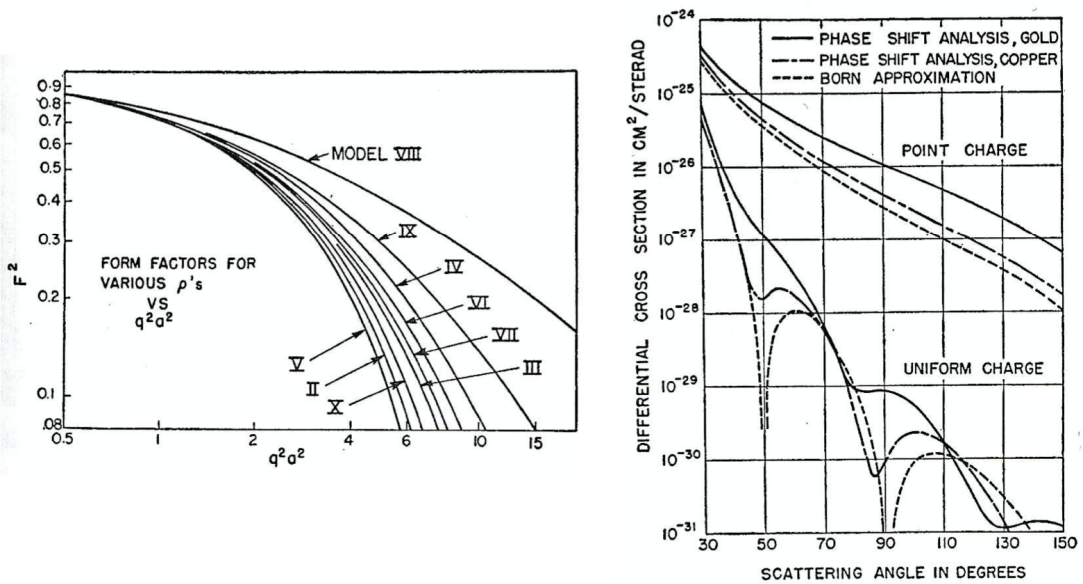
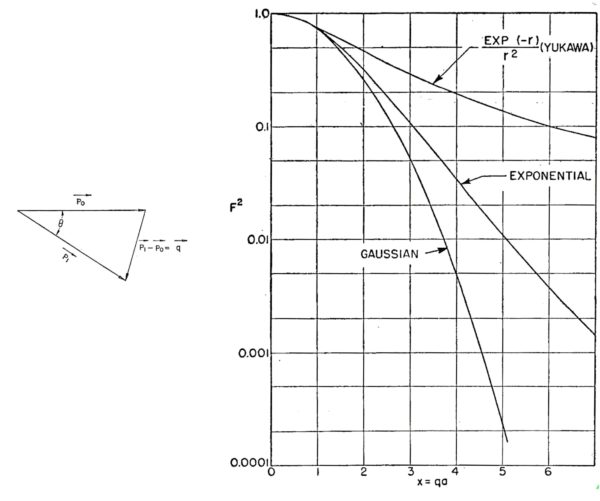
図 4. では, 有用な電荷分布の $q a$ が小さい値のときの形状因子の2乗を幾つか示してある．
図 5. では Yenniなどに拠る, 金と銅の一様球モデルの場合の位相シフト分析である．全ての場合について, 点電荷曲線とボルン近似結果が表示されている．

ほとんど全ての有用な核の形状は, 表 I に掲げられた何れかのモデルに含まれるか, またはほとんど同等に近いものである．しかし, 表 I で反発コアモデルを十分に近似できる項目はないかも知れない．表 I には(形状因子の)幾つかが表示されている．現著者が通常行うボルン近似法を用いた手続きは, 軽い原子核の実験データを幾つかの簡単な核モデルにフィットさせることである．適切なモデルを探すと, すぐに表 I に記載されている内の一つか二つに絞ることが出来る．次にパラメータ(または複数のパラメータ)の最適な適合を行うのである．
逆の手続きを行って, 実験的な形状因子から電荷分布を計算することも可能である．D.G.Ravenhall は $C^{19}$ の正確なデータを解析することでこれを実行した．実験データが非常に正確である場合,この手続きは有用である．著者の意見では, 現在の正確度では多くの場合この方法は保証できない．しかしながら, この手続きが有益となる時期が来るのにそれほど長くはかからないはずである．式(17)の逆は次となる：

\begin{matrix} (20) & ρ (r) = \frac{1}{(2 π)^{3}} \int F (q) e^{- i q \cdot r / ℏ} d^{3} q = \frac{1}{2 π^{2}} \int_{0}^{\infty} F (q) \frac{\sin (q r / ℏ)}{q r / ℏ} q^{2} d q \end{matrix}

Schiff は,「もし正しいモデルが選択されれば, 形状因子

F

と一致するはずの特定な実験量と

F

を比較する便利な適合手順」も提示した．

(c) 電子散乱の位相シフト分析

Yennie, Ravenhall, Wilson, Brenner, Brown, Elton, Elizabeth Baranger は, 以下のことを最終的に示した：中間的元素及び重元素のほとんどの核モデルに於いて, 厳密な弾性散乱断面積は第1ボルン近似で与えられる断面積から著しく逸脱する．主な相違のタイプは2つあるようだ．Yennie たちの論文から引用した図 5 にはその両方が現れている．図 5 の右図は, エネルギーがおよそ $150$ MeV に相当する金の一様電荷分布と, エネルギーがおよそ $225$ MeV に相当する銅の同じ電荷分布についてのものである(refer to)．まず, 形状因子にボルン近似では本当のゼロが出てくるけれど, 正確な計算では真のゼロではなく極小値が現れる．また, ある場合には第1ボルン近似のゼロに相当して出現するのは単なる屈曲点(inflection)となる．第2に, 一般にボルン近似から求まる半径は正確な計算の半径よりも大きい．入射電子のドブロイ波は核の電磁場中では自由な場合に比べ短くなるという事実に気付けば, これはもっともな事と思われる．それは, 電磁場中ではポテンシャルが最低な値となるので, 有効な運動エネルギーが場中では場の外よりも大きくなるであろうという単純な考察からである．ボルン近似はこの事実を考慮に入れていない．全ての長さは $λ / 2 π$ 単位の電子によって測定され, $λ / 2 π$ は核の場から影響を受けないので, ボルン近似では核は実際よりも大きなものとなる．言い換えると, 回折特性(diffraction feature) は与えられた $q R$ の値と結び付いている．ただし $R$ は典型的な半径パラメータである． $q R \propto 2 π R / λ$ なので, もし自由空間中よりも $λ / 2 π$ 値が小さいならば, 得られる回折特性からは小さな $R$ 値を得るであろう(すなわち $2 π R / λ$ が同じなら $λ / 2 π$ が小さいと $R$ も小さくなる)．このタイプの議論は Yennieたちによって与えられた．しかし, 後になって Gaussian 型及び指数型の電荷分布は, 期待される振舞いとは一致しないことが分かっている．「恐らくその理由は, ガウス型及び指数型の電荷分布は単調な角運動量を与えるために回折特性は示さないのである」というのが一見そつのない言い方である．この問題は散乱現象の物理特性を理解する上で興味深いものであり, 近いうちにその解明がなされることが期待される．
ともかく, 第1ボルン近似は重い元素に用いることは出来ないことが立証された．図 4 の右図から, 決して十分とは言えないけれど, 銅では金の場合よりずっと一致していることが分かる．特に一致が悪いのは回折が極小点の近傍であるが, それはボルン近似では真にゼロとなる位置に相当する． $Z$ が $10$ よりも小さい核の場合, ボルン近似はゼロ付近以外なら十分な近似となっている．なぜ第1ボルン近似が良くないかの理由の一つを指摘したのは Yennieたちであった．彼らは, 一般的に複素数である散乱振幅が, 金の場合にはボルン近似の散乱振幅から大きくズレることを見出した．ボルン近似の場合, 散乱振幅は正または負の実数で, 回折が極小の点でゼロとなる．彼らの論文から採った図 6 は, 表 I のタイプ II のモデルについて, 極座標で角度 arg $f (θ)$ に対する散乱振幅係数 $f (θ)$ の $\log_{10}$ プロットの典型的な概形を示したものである．

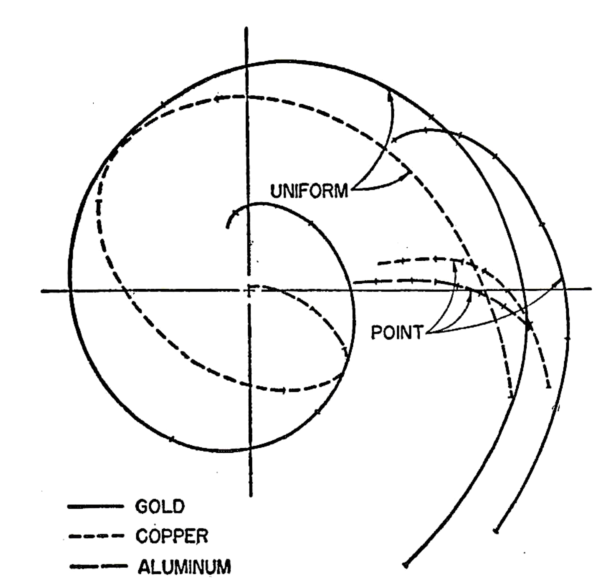
図 6. 金,銅,アルミニウムの点散乱の場合を極座標に於いて角度arg $f (θ)$ に対する $\log_{10} | f (θ) |$ , 及び金と銅の一様モデルで $k R = 5.4$ の場合をプロットしたもの．各々の曲線には $θ = 30$ °から $20$ °毎の値が示されている．アルミニウムの場合には実際の数値に最も近い結果を与えており, これは軽い核の場合にはボルン近似が妥当であることを示している．

図 7. Fermiモデル. $c$ は半値密度点であり $t$ は表面厚 ( $90$ %- $10$ % 距離) である

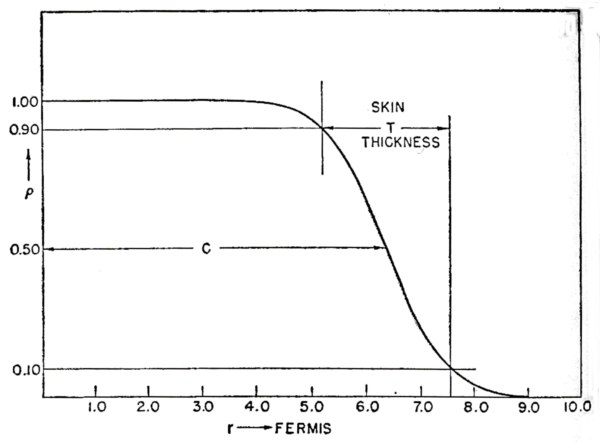
ボルン近似は中間の元素及び重元素に用いることが出来ないし, また簡単な他の近似法がまだ開発されていないので, 現時点では精密な位相シフト法を用いなければならない．少なくとも今までのところ, 実験データをフィッテングするのに利用出来る方法は, モデルを選択して角度分布を計算する以外にないようである．もし実験との差異が見られたら, モデルを変更して新たに計算する．この試みを繰り返すことで, 一つまたは関係する一連のモデルに落ち着く．この手順は Yennieたちの論文に書かれており, それには「Fermiの平滑化された一様モデル」が導入されている．この特別なモデルは[式(21)の] フェルミ型関数の形状をしており, その典型的な概形が図 7 に示されている．後で分かることであるが, このモデルは中間元素と最重量核の実際の形にかなり近いようである．

\begin{matrix} (21) & ρ (r) = \frac{ρ_{1}}{\exp (\frac{r - c}{z_{1}}) + 1} \end{matrix}

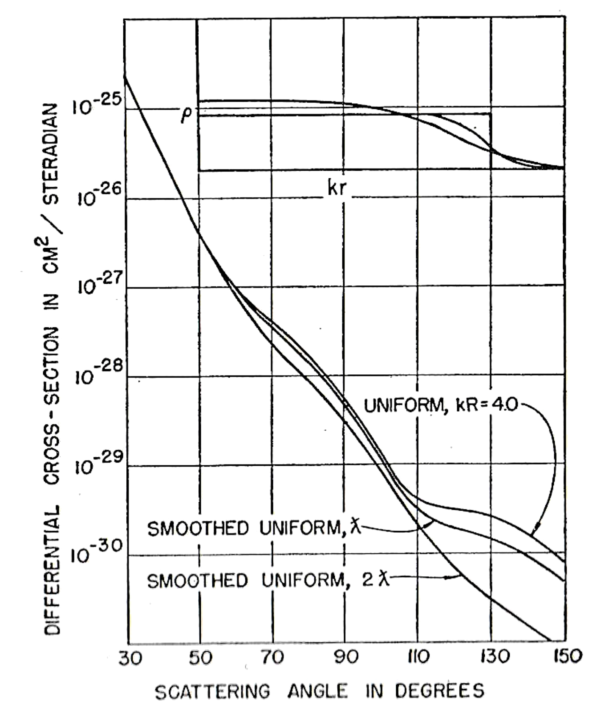
図 8. 金について $k R = 4.0$ の一様モデルと, ２つの平滑化された一様モデルの $K \equiv 1 / z_{1} = 4.40, c = 3.86$ 及び $K = 2.20, c = 3.51$ であるときの $125$ MeVに於ける散乱断面積, 及び, その実験データである．2番目と3番目の形はこのエネルギーで表面厚 $t$ が $λ / 2 π$ と $λ / π$ の場合である．ただし $λ / 2 π = 1 / k$ である．３つの形の r.m.s.半径は全て $3 λ / 2 π$ である．はめ込み図は, スケーリングした $ρ$ を描いたものである．

実験データに適合する最適なモデルを決定するのに, 図 7 のようなグラフを調べることが役に立つ．図 7 には３つの電荷分布がはめ込まれており, そして金の約 $125$ MeVの場合について位相シフト法による３つの電荷分布に相当する理論的な角度分布が示されている．一様荷電球(四角い端)が最も顕著な回折的な特徴を示している．予想通りに, 最も滑らかな角度分布を示すのは曲線が最も滑らかなときである．Brown とElton は同類のモデルについて計算を行ない似た結果を得ている．Hill, Freeman, Ford は少しだけ違うモデルを用いた類似な計算を実行し, やはり同じ種類の結果を得ている．Glassgold はより簡単なモデルを取り扱っている．
Yennieたちと Brennerたちの計算について, 幾つかの簡単な説明をしておくのが適切であろうと思う．これらの著者たちは, 球対称で静的な電荷分布について Dirac方程式を用いて計算した．4重極的な歪み(quadrupole distortions)は特に回避し, また可能な分散補正または相関などの他の力学的効果は考慮していない．分散補正(dispersion corrections)については Schiff が考察し, それらは小さいはずであることを指摘している．理論中に含まれている暗黙の仮定, すなわち(viz), ディラック方程式は散乱に適用できる, 電荷分布は静的なものとして扱える, 電子核子間に電磁気学的でない力は存在しない, クーロン則は微小な距離でも有効であるなど, は幾つかのエネルギー値での散乱実験と理論との整合性, 及び, これらの結論と核物理学の他の部門で見出された結論との整合性に依ってしかテストすることが出来ない．これまでのところ, 恐らく陽子の場合を除いて, これらの単純な仮定の適切さを疑う理由は無いようである (Sec.VII を見よ)．
Lewis は非ポテンシャルによる散乱を研究しているが, 彼は最近, 原子核中の陽子間の相関を検討し, また第２ボルン近似についての詳細な研究を幾つか提示している．

(19) 例えば，Z.G.Pinsker Electron Diffraction (ButterWorth Scientific Publication, London, 1953), p.148,Eq.(7-25).
(20) G.E.Brown and L.R.B.Elton, Pil. Mag. \textbf{46}, 164 (1955)．
(21) A.E.Glassgold, Phys. Rev. 98, 1360 (1955)．
(22) L.I.Schiff, Phys. Rev. 98, 756 (1955)．
(23) R.R.Lewis,Jr., Phys. Rev. 102, 544 (1956)．
(24) R.R.Lewis,Jr., Phys. Rev. 102, 537 (1956)．

2025年5月
月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31