
第7章では「汎関数微分」を導入して議論が為されている.「汎関数微分」は少し分かりづらいと感じたのでその補足として Swanson の文章とウィキペディアの説明文を紹介しておこう.
(1) 先ずは、Mark S. Swanson : 「Path Integrals and Quantum Proceses」の § 1.3 の一部を抜粋したものを示す:
実関数は, ある空間から実数へのマッピングである.関数自身は無限大次元空間に於ける点と見做すことが出来る.この類似性から, 「汎関数」( functional )を「関数または関数多項式の数値へのマッピングである」と定義する.関数は汎関数によってマッピングされた座標の役割 (通常の関数
汎関数を歴史的極限とする関数の性質を決定することで変分計算が生まれた ( Determining the nature of the functions that extremize the functional historically led to the calculus of variations ).関数の極値を見出す問題との類推から ( by analogy to ), 関数の極限形を決定するには汎関数微分及び汎関数微分係数を定義する必要がある.一度これらの定義が為されると, 極限関数が満たしておくべき局所的な候補または各点ごとの候補を生成することが可能となる (it is possible to create a local or pointwise criterion that extremum functions must satisfy).[ 日本語ウィキによれば, ある汎関数が, その勾配やラプラシアン或いは他の高階微分に依存しないとき, その汎関数は局所的(local)であると言うらしい ].この定義を行うために, 先ずは最も簡単な場合で考察する.そこで, 単一の関数
ただし
式 (sw-1) の定義は, 通常の微分操作が有する特性を全て持っている.例えば, もし
ただしこれ以降では, 積分端 ( limits of integration ) の明示はしないことにする.式 (sw-3) の両辺に任意のベキの汎関数微分を作用させて
任意の汎関数は, その汎関数微分が性質の良いような( well-defined )関数による式 (sw-4) の形式によって展開することが可能である.
式 (sw-4) は汎関数微分の定義も可能とする.関数
ただしオーダー
また, 引数である関数
この定義は, 通常の多変数関数の微分と形式的に全く類似している.そこでの関数
ただし
で表されることを考えるならば, 式 (sw-6) の積分は「関数
汎関数のチェーン・ルール (合成関数の微分則) は, 汎関数
上式と微分の標準的な形 (sw-6) との比較から, 次のようなチェーン・ルールが成り立つと言える:
これら全ての定義を一つ以上の関数の汎関数の場合に拡張するのは誠に容易である.一般的な場合, 汎関数
しかしながら, 表現式
ただし添字
(2) 次は, 日本語のウィキペディアの記述である:
数学及び理論物理学に於ける汎関数微分(functional derivative)は,「方向微分」(directional derivative)の一般化である.方向微分が有限次元のベクトルに関する微分法であるのに対して, 汎関数微分は (無限次元ベクトルとしての)連続関数に対する微分法を与えるとされるが, 単純な1変数微分積分学に於ける1次元の微分を一般化したものと見做せる点では共通している.汎関数微分の数学的に厳密な取り扱いは関数解析学に属する.
そして汎関数の定義式として次式が提示される:
の汎関数微分 とは, 任意の試験関数 に対して次式を満たすようなシュバルツ超関数を言う:
ただし左辺の記号は と の内積を表している.試験関数 の処に の第1変分 を代用して, 汎関数 の微分( differential )すなわち 第1変分( first variation ) が得られることは, 傾き( gradient )から関数の微分が得られるのと同様である:
また, ノルムの試験関数 を用いれば, この関数に沿った方向微分が得られる.
更に, 汎関数微分の例として, 関数とその導関数を含む式の積分として書けるような汎関数に対する汎関数微分の公式を挙げている.それは「オイラー=ラグランジュ方程式の一般化」であるそうだ.
与えられた汎関数が次の形をしているとする:
ただしが の境界で消えるものとする.すると, 汎関数微分と試験関数 との内積は次の形に書くことが出来る:
ここで, 3行目は積分の限界に於いてと仮定した.故に, 汎関数微分は次となる:
テル・ハール:「解析力学」では, この式 (5) を以って汎関数微分の導入としている:
(3) 「汎関数微分は方向微分の一般化である」ことが分かったので, 参考のためにその「方向微分」について, 安達:「ベクトル解析」§ 32. から抜粋した文章を示しておく.
スカラー点関数を
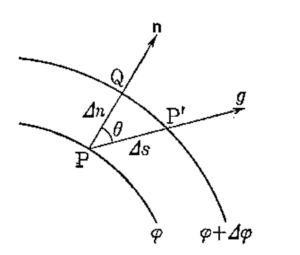
P, P’ の座標を
ここで,
ゆえに,
よって,
直線

