
Problem 6-12
Assume that is independent of time and show that the time integral of the second-order scattering term gives
where the points and are arranged as shown in Fig. 6-9. The term stands for the distance between the point and , etc. Assume that becomes negligibly small at distances which are short compared to or . Show that the cross section is given by , where the scattering amplitude , including the first-order term, is
where is the momentum of the electron traveling in the direction of and is the momentum of an electron traveling in the direction . The magnitude of the momentum is , and it is approximately unchanged by an elastic scattering of the electron from the ( relatively massive ) atom.
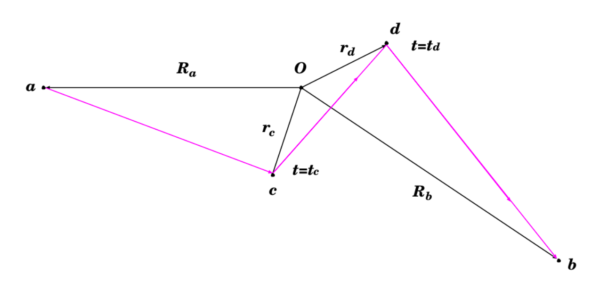
(Fig. 6-9) To increase the accuracy of scattering calculations, we can take account of second-order terms in the perturbation expansion.
Here, as in Fig. 6-2 (3), we picture the electron as being scattered at two separate points in the atomic potential. Thus the electron starts at ; proceeds as a free particle to , where it is scattered; then moves as a free particle to , where it is scattered again; and finally moves as a free particle to , where it is collected by the counter. The points and can lie at any position in space. The atomic potential at these positions depends upon the radius vectors and , measured from the center of the atom .
(解答例) 式 (6-17) から,2 次の散乱項 は次である:
ここで とする.( 原書では, § 6-1 の一般的な摂動展開を議論での図 6-2 と,この問題の配置図 6-9 で点 と点 の位置が逆になっているので注意する! ).
式 (6-33) の を求めたときと同様に考えて, 自由粒子核 の各々は式 (3-52) を 3 次元化したものを用いて次とする:
ただし時間については, 暗黙の内に を仮定しているので の時間積分範囲は とし, の時間積分範囲は とすればよい.また,,, と表記し直すことにする.これらを式 (1) に適用すると次となる:
まず についての時間積分 を実施する:
巻末付録の「役立つ定積分」の公式 (A-5) を用いる.この場合の は,
従って,
この結果を式 (3) に代入し, 今度は についての時間積分を行う.やはり公式 (A-5) を同様に用いると次となる:
これを式 (3) に代入すると, が式 (6-58) のように得られる:
今度は,2次までの散乱振幅 を考える.ただし は式 (6-44) 中のものである:
は式 (6-42) を求めたときと同様な議論により求められる.ただし式 (6-58) の に等価な式に於いては なので, 次のような近似を用いよう:
すると は, 近似的に次のように書くことが出来る:
この絶対値の 2 乗 と は,
となるから, 式 (6-42) を求めたときと同様にして次が得られる:
従って, 式 (6-42) との比較から, この場合の に相当するのは次である:
従って, 式 (6-44′) との類推で,2次のボルン散乱振幅 は次とすることが出来る:
更に指数関数中の量 は, であることに注意する.また,
とすることで, 次のように近似できる:
すると式 (9) の積分部分 は, 次のように近似して書くことが出来る:
これから位相因子を除去したものを とするならば,「
2次のボルン散乱振幅」 は次のように書くことが出来る:
( 参考 ) この2次のボルン振幅 に対応するものが J.J.Sakurai に書かれている.その中の § 7.2 の式 (7.2.23) である:
この式中の として § 7.1 の式 (7.1.12) を代入するならば, 記事の式 (11) となる:
以上の結果と式 (6-44′) とから, 散乱振幅 は問題文の式 (6-59) のように書ける:
(注) Emended Edition by D.F.Styer では, 式 (6-58) において が挿入されており, またその結果として式 (6.59) にも因子 が挿入されている !?.これは, ぼっとすると に式 (6-13) ではなくて式 (6-7) の方を直接用いてしまったからかも知れない ?! .両者には因子 の違いがある.詳しくは, 前に書いた記事:「付録:「役に立つ定積分」に追加された公式 (A.12) について」を参照してほしい.



