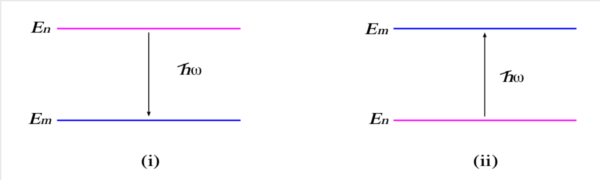問題 6-24 の解答例

Problem 6-24
Suppose that the potentical $V$ is periodic in time. For example, suppose $V (x, t) = V (x) (e^{i ω t} + e^{- i ω t})$ .　Show that the probability for a transition to take place is small unless the final state is one of the two values
(1) $E_{f i n a l} = E_{i n i t i a l} + ℏ ω$ 　(corresponding to an absorption of energy),
or
(2) $E_{f i n a l} = E_{i n i t a l} - ℏ ω$ 　(corresponding to the emmission of energy).
This means that Eq. (6-86) is unchanged, but the density of states $ρ (E)$ must be calculated at these new values of $E$ .　Or, in analogy with Eq. (6-87), we have

\begin{matrix} (6-94) & \frac{d P (n \to m)}{d t} = \frac{2 π}{ℏ} {| M_{n \to m} |}^{2} [δ (E_{m} - E_{n} - ℏ ω) + δ (E_{m} - E_{n} + ℏ ω)] \end{matrix}

(解答)　この問題は J.J.Sakuraiの § 5.6 の「調和摂動」からの抜粋を記すことで解答に代えることにする．
「調和摂動」(harmonic perturbation) と言われる正弦的時間変化をする次のポテンシャルを考察する：

\begin{matrix} (1) & V (t) = V e^{i ω t} + V^{†} e^{- i ω t} \end{matrix}

ここで

V

は

x, p, s

などに依存していてもよい．この問題では

V = V (x)

である．実は, 前に書いたブログ記事：「時間に依存するポテンシャル問題」の中で記述した 2 準位問題の系もこの時間に依存するこの種のポテンシャルに相当している．
　始状態は

H_{0}

の 1 つの固有状態

| n ⟩

であると仮定する．摂動 (1) が

t = 0

で印加されたとすると, 時間間隔

T

間の1次の振幅は次である：

\begin{aligned} c_{m}^{(1)} & = - \frac{i}{ℏ} \int_{0}^{T} d t e^{i ω_{m n} t} (V_{m n} e^{i ω t} + V_{m n}^{†} e^{- i ω t}) \\ (2) & = V_{m n} \frac{1 - e^{i (ω_{m n} + ω) T}}{ℏ ω_{m n} + ℏ ω} + V_{m n}^{†} \frac{1 - e^{i (ω_{m n} - ω) T}}{ℏ ω_{m n} - ℏ ω} \end{aligned}

ただし

V_{m n}

と

V_{m n}^{†}

は

V

の行列要素である：

\begin{matrix} (3) & V_{m n} = \int_{- \infty}^{\infty} d^{3} r ϕ_{m}^{*} (r) V (r) ϕ_{n} (r), V_{m n}^{†} = \int_{- \infty}^{\infty} d^{3} r ϕ_{m}^{*} (r) V^{†} (r) ϕ_{n} (r) \end{matrix}

すると, このときの遷移確率

P (n \to m)

は次となる：

\begin{aligned} P (n \to m) & = | c_{m}^{(1)} |^{2} = c_{m}^{(1) †} c_{m}^{(1)} \\ = (V_{m n}^{†} \frac{1 - e^{- i (ω_{m n} + ω) T}}{ℏ ω_{m n} + ℏ ω} + V_{m n} \frac{1 - e^{- i (ω_{m n} - ω) T}}{ℏ ω_{m n} - ℏ ω}) (V_{m n} \frac{1 - e^{i (ω_{m n} + ω) T}}{ℏ ω_{m n} + ℏ ω} + V_{m n}^{†} \frac{1 - e^{i (ω_{m n} - ω) T}}{ℏ ω_{m n} - ℏ ω}) \\ = | V_{m n} |^{2} \frac{4 \sin^{2} (ω_{m n} + ω) T / 2}{(ℏ ω_{m n} + ℏ ω)^{2}} + e^{i ω T} V_{m n}^{2} \frac{4 \sin (ω_{m n} - ω) T / 2 \sin (ω_{m n} + ω) T / 2}{(ℏ ω_{m n} - ℏ ω) (ℏ ω_{m n} + ℏ ω)} \\ + e^{- i ω T} V_{m n}^{† 2} \frac{4 \sin (ω_{m n} - ω) T / 2 \sin (ω_{m n} + ω) T / 2}{(ℏ ω_{m n} - ℏ ω) (ℏ ω_{m n} + ℏ ω)} + | V_{m n} |^{2} \frac{4 \sin^{2} (ω_{m n} - ω) T / 2}{(ℏ ω_{m n} - ℏ ω)^{2}} \end{aligned}

ただし, この問題では

V = V^{†} = V (x)

であるから次となる：

\begin{aligned} P (n \to m) & = | c_{m}^{(1)} |^{2} = c_{m}^{(1) †} c_{m}^{(1)} \\ = | V_{m n} |^{2} (\frac{4 \sin^{2} [(ω_{m n} + ω) T / 2]}{(ℏ ω_{m n} + ℏ ω)^{2}} + 8 \cos ω T \frac{\sin [(ω_{m n} - ω) T / 2] \sin [(ω_{m n} + ω) T / 2]}{(ℏ ω_{m n} - ℏ ω) (ℏ ω_{m n} + ℏ ω)} \\ + \frac{4 \sin^{2} [(ω_{m n} - ω) T / 2]}{(ℏ ω_{m n} - ℏ ω)^{2}}) \end{aligned}

これらの式は, 一定値

V (t) = V, (t > 0)

をとる摂動の場合の次の式

\begin{aligned} (4.a) & c_{m}^{(1)} = - \frac{i}{ℏ} V_{m n} \int_{0}^{T} d t e^{i ω_{m n} t} = V_{m n} \frac{1 - e^{i ω_{m n} T}}{ℏ ω_{m n}} = V_{m n} \frac{1 - e^{i ω_{m n} T}}{E_{m} - E_{n}} \\ (4.b) & P (n \to m) = | c_{m}^{(1)} |^{2} = | V_{m n} |^{2} \frac{4 \sin^{2} [ω_{m n} T / 2]}{(ℏ ω_{m n})^{2}} = \frac{| V_{m n} |^{2}}{(E_{m} - E_{n})^{2}} [4 \sin^{2} \frac{(E_{m} - E_{n}) T}{2 ℏ}] \end{aligned}

に似ている．これに相当する

λ_{m n}^{(1)}

に対する式は, 本文の式 (6-78) 及び式 (6-79) である．従って, 必要な変更は

\begin{matrix} (5) & ω_{m n} = \frac{E_{m} - E_{n}}{ℏ} \to ω_{m n} + ω and ω_{m n} - ω \end{matrix}

で置き換えた2つの場合を足し合わせることである．これの変化は, 本文の図 6-13 のグラフを

+ ω

または

- ω

だけ平行移動したグラフを足し合わせたものとなる (下図 1 を参照)．

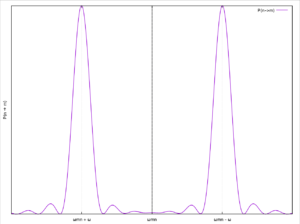
図 1. 調和摂動に於ける遷移確率曲線の概形である．

従って, そのグラフから，

T \to \infty

のとき，

| c_{m}^{(1)} |^{2}

がかなり大きな値を持つのは, 次のときのみである：

\begin{array}{r} (6.a) & ω_{m n} + ω ≃ 0, ⟶ E_{m} ≃ E_{n} - ℏ ω, \\ (6.b) & ω_{m n} - ω ≃ 0, ⟶ E_{m} ≃ E_{n} + ℏ ω, \end{array}

式 (6.a) が満足され式 (4.a) が重要なときはいつも, 第 2 項は明らかに重要でなく, その逆も成り立つ．エネルギー保存の条件は, 量子力学系だけで満たされているのではなく, 外見上欠けているエネルギーの保存は, 「外部」ポテンシャル

V (t)

へ与えるエネルギー

—

または

V (t)

から取り入れるエネルギー

—

によって償われている．これを図で表わすと下図 2 のようである．

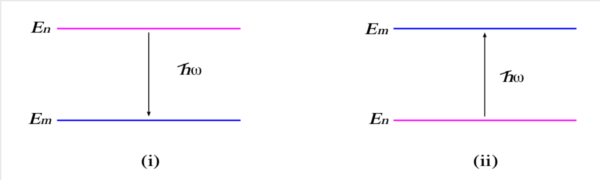
図 2.　(i) 誘導放出：量子力学系が $V$ に $ℏ ω$ を与える．(初期状態が励起状態であるときのみ可能)． (ii) 吸収：量子力学系が $V$ から $ℏ ω$ を受け取り励起状態になる．

第 1 の場合 (誘導放出)では, 量子力学系がエネルギー

ℏ ω

を

V

に与える．これが可能なのは明らかに始状態が励起しているときのみである．第 2 の場合 (吸収)では, 量子力学系が

V

からエネルギー

ℏ ω

を受け取り, 励起状態になる．このように時間に依存する摂動は, エネルギーを幾らでも遣り取りする「湧き出し」乃至「吸い込み」と見做すことが出来る．
　遷移率に関しては, 式 (6-86) と全く良く似た形をした式が成り立つ：

\begin{aligned} (7.a) & (放 出 率) ： w_{n \to [m]} = \frac{2 π}{ℏ} \overset{―}{| V_{m n} |^{2}} ρ (E_{n}) |_{E_{m} ≃ E_{n} - ℏ ω} \\ (7.b) & (吸 収 率) : w_{n \to [m]} = \frac{2 π}{ℏ} \overset{―}{| V_{m n}^{†} |^{2}} ρ (E_{n}) |_{E_{m} ≃ E_{n} + ℏ ω} \end{aligned}

あるいはもっと共通な形では次のように表せる：

\begin{matrix} (8) & w_{n \to m} = \frac{2 π}{ℏ} {\begin{matrix} | V_{m n} |^{2} \\ | V_{m n}^{†} |^{2} \end{matrix}} δ (E_{m} - E_{n} \pm ℏ ω) \end{matrix}

また，

| V_{m n} |^{2} = | V_{n m}^{†} |^{2}

にも注意すべきである．これは

⟨ n | V^{†} | m ⟩ = ⟨ m | V | n ⟩^{*}

の帰結である．このことと式 (7) とから, 次が言える：

\begin{matrix} (9) & \frac{2 π}{ℏ} \overset{―}{| V_{m n} |^{2}} = \frac{n \to [m] の 放 出 率}{[m] の 終 状 態 密 度 : ρ (E_{[m]})} = \frac{[m] \to n の 吸 収 率}{[n] の 終 状 態 密 度 : ρ (E_{[n]})} \end{matrix}

ただし吸収の場合には

n

が終状態を表わすようにしているので注意する．放出と吸収との間の対称性を表わしているこの式は「詳細つりあいの式」と呼ばれている．
　この問題では

V = V (x)

であるから, 式 (8) において

| V_{m n} |^{2} = | V_{m n}^{†} |^{2}

となる．それらを同じ

| M_{n \to m} |^{2}

と記すならば, 問題文の式 (6-94) のように表わせることになる：

\begin{matrix} (6-94) & w_{n \to m} = \frac{d P (n \to m)}{d t} = \frac{2 π}{ℏ} | M_{n \to m} |^{2} [δ (E_{m} - E_{n} - ℏ ω) + δ (E_{m} - E_{n} + ℏ ω)] \end{matrix}

または, 本文の式 (6-86) から式 (6-87) までの説明にあるように, 上式 (6-94) は「

\int d E_{m} ρ (E_{m})

で積分されるべきもの」と理解しなければならないので, 上式は次のように書き表すことも出来る：

\begin{aligned} \frac{d P (n \to m)}{d t} = \int_{- \infty}^{\infty} d E_{m} ρ (E_{m}) \frac{2 π}{ℏ} | M_{n \to m} |^{2} [δ (E_{m} - E_{n} - ℏ ω) + δ (E_{m} - E_{n} + ℏ ω)] \\ = \int_{- \infty}^{\infty} d E_{m} ρ (E_{m}) \frac{2 π}{ℏ} | M_{n \to m} |^{2} δ (E_{m} - E_{n} - ℏ ω) + \int_{- \infty}^{\infty} d E_{m} ρ (E_{m}) \frac{2 π}{ℏ} | M_{n \to m} |^{2} δ (E_{m} - E_{n} + ℏ ω) \\ (6-94′) & = \frac{2 π}{ℏ} | V_{m n} |^{2} ρ (E_{n} + ℏ ω) + \frac{2 π}{ℏ} | V_{m n} |^{2} ρ (E_{n} - ℏ ω) \end{aligned}

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31