\(\textit{Eleventh Lecture}\)
\(\beta\) と \(\mathbf{\alpha}\) がエルミートであるのは, 特定の表現 (in certain representations) に於いてのみであることに注意するべきである．特に, これまでの表現ではエルミートである．これを「標準表現」 (Standard Representation) と呼び, 適切な場合にはこの表現に S.R. というラベルを付ける．電荷及び電流の密度に対する表現として
\(
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\half{\frac{1}{2}}
\newcommand\Braket[1]{\left\langle #1 \right\rangle}
\)
\begin{equation}
\rho=\psi^{*}\psi,\quad \mb{j}=c\psi^{*}\mb{\alpha}\psi, \qquad \mathrm{S.R.}
\tag{11-1}
\end{equation}
\rho=\psi^{*}\psi,\quad \mb{j}=c\psi^{*}\mb{\alpha}\psi, \qquad \mathrm{S.R.}
\tag{11-1}
\end{equation}
を得るには \(\mb{\alpha}\) と \(\beta\) のエルミート性が必要である．従って「これらは全ての表現でエルミートである」と言う訳ではない．ディラック方程式は (\(\hbar,c\) を回復した場合) 次である [1]Schiff (“Quantum Mechanics,” McGraw-Hill, New York, 1949) のハミルトニアンは, ここでのハミルトニアンと違ってマイナス符号が \(e\phi\) … Continue reading ：
\begin{equation}
i\hbar\ppdiff{\psi}{t}=H\psi,\qquad
H=\beta mc^{2} + e\phi + c\mb{\alpha}\cdot\left[-i\hbar\nabla-\frac{e}{c}\mb{A}\right]
\tag{11-2}
\end{equation}
i\hbar\ppdiff{\psi}{t}=H\psi,\qquad
H=\beta mc^{2} + e\phi + c\mb{\alpha}\cdot\left[-i\hbar\nabla-\frac{e}{c}\mb{A}\right]
\tag{11-2}
\end{equation}
\(\psi\) が 4成分の波動関数であることを思い起こすと, \(x\) の期待値は,
\begin{equation*}
\langle x \rangle =\int \psi^{*}x\psi\,dV
=\int \bigl(\psi_{1}^{*}x\psi_{1}+\psi_{2}^{*}x\psi_{2}+\psi_{3}^{*}x\psi_{3}
+\psi_{4}^{*}x\psi_{4}\bigr)\,dV\qquad \mathrm{S.R.}
\end{equation*}
\langle x \rangle =\int \psi^{*}x\psi\,dV
=\int \bigl(\psi_{1}^{*}x\psi_{1}+\psi_{2}^{*}x\psi_{2}+\psi_{3}^{*}x\psi_{3}
+\psi_{4}^{*}x\psi_{4}\bigr)\,dV\qquad \mathrm{S.R.}
\end{equation*}
である．同様にして次式が証明出来るが, それは練習問題としておこう [2][ブログ註] \(\alpha_1,\psi,\psi^{*}\)に具体的な行列表現を代入するだけである： \begin{align*} \psi^{*}\alpha_1\psi &=\begin{pmatrix}\psi^{*}_{1}\!\!\! & … Continue reading ：
\begin{align*}
\langle \mb{\alpha}\rangle &= \int \psi^{*}\mb{\alpha}\psi\,dV,\\
\langle \alpha_x\rangle &= \int \bigl(\psi^{*}_{4}\psi_{1}
+\psi^{*}_{3}\psi_{2}+\psi^{*}_{2}\psi_{3}+\psi^{*}_{1}\psi_{4}\bigr)\,dV
\qquad \mathrm{S.R.}
\end{align*}
また, 行列要素は形式的には前と同様である．例えば,
\begin{equation*}
\bigl(\mb{\alpha}\bigr)_{mn}=\int \psi^{*}_{m}\mb{\alpha}\psi_{n}\,dV
\end{equation*}
\bigl(\mb{\alpha}\bigr)_{mn}=\int \psi^{*}_{m}\mb{\alpha}\psi_{n}\,dV
\end{equation*}
もし \(A\) が何らかの (Heisenberg表示の) 演算子であるならば, その時間微分 (Heisenbergの運動方程式) は次となる：
\begin{equation*}
\dot{A}=\frac{i}{\hbar}[H,A]+\ppdiff{A}{t}=\frac{i}{\hbar}\bigl(HA-AH\bigr)+\ppdiff{A}{t}
\end{equation*}
\dot{A}=\frac{i}{\hbar}[H,A]+\ppdiff{A}{t}=\frac{i}{\hbar}\bigl(HA-AH\bigr)+\ppdiff{A}{t}
\end{equation*}
\(A=\mb{x}\) である場合, (\(\mb{x}\) は時間に依存しないので) その結果が次となることは明らかだ [3][ブログ註] 時間発展演算子を \(\mathscr{U}(t)=\exp(-iHt/\hbar)\) とするならば, シュレディンガー表示の観測量 \(A\) のハイゼンベルグ表示は … Continue reading ：
\begin{equation}
\dot{\mb{x}}=\frac{i}{\hbar}\bigl(H\mb{x}-\mb{x}H\bigr)= c \mb{\alpha}
\tag{11-3}
\end{equation}
\dot{\mb{x}}=\frac{i}{\hbar}\bigl(H\mb{x}-\mb{x}H\bigr)= c \mb{\alpha}
\tag{11-3}
\end{equation}
なぜなら, ハミルトニアン \(H\) 中の \(\mb{p}\cdot\mb{\alpha}\) 以外の項は全て \(\mb{x}\) と交換するからである：
\begin{align*}
H x_i-x_i H
&=\left\{\beta mc^{2}+e\phi+c\mb{\alpha}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right\} x_i
-x_i \left\{\beta mc^{2}+e\phi+c\mb{\alpha}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right\}\\
&=c(\mb{\alpha}\cdot\mb{p}) x_i – c x_i (\mb{\alpha}\cdot\mb{p})
=c(\alpha_1 p_1+\alpha_2 p_2 + \alpha_3 p_3) x_i -c x_i (\alpha_1 p_1+\alpha_2 p_2 + \alpha_3 p_3)\\
&=c\alpha_1 (p_1x_i-x_ip_1) + c\alpha_2 (p_2 x_i-x_ip_2) + c\alpha_3 (p_3x_i-x_ip_3)\\
&=c\alpha_1 \frac{\hbar}{i}\delta_{1i}+c\alpha_2 \frac{\hbar}{i}\delta_{2i}
+c\alpha_3 \frac{\hbar}{i}\delta_{3i}=c\frac{\hbar}{i}\sum_{j}\alpha_j \delta_{ji}
=c\frac{\hbar}{i}\alpha_i,\\
\rightarrow\quad \dot{x}_{i}&=\frac{i}{\hbar}\times c\frac{\hbar}{i}\alpha_i = c\alpha_i
\end{align*}
しかし, \(\mb{\alpha}^{2}=1\) であるから \(\mb{\alpha}\) の固有値は \(\pm1\) である．従って \(\dot{x}\) の固有速度は, 光速度を \(c\) として \(\pm c\) である．この結果はときどき, 速度の正確な決定は「２つの時間に於ける正確な位置決定」を意味するという議論により妥当とされる．すると不確定性原理により, 運動量は完全に不確定となり, どの値も等しく可能性がある．速度と運動量の相対論的関係から, 光速に近い速度がより可能性が高く, 極限では速度の期待値が光の速さになることが分かる [4]この議論は完全に受容できると言うわけではない．なぜなら \(\dot{\mb{x}}\) は \(\mb{p}\) と交換する．即ち, 同時に … Continue reading．
同様にして, 力学的運動量 \(\displaystyle \mb{\pi}=\mb{p}-\frac{e}{c}\mb{A}\) の \(x\) 成分に対しては,
\begin{align*}
\dot{\mb{\pi}}_x
&=\frac{i}{\hbar}\bigl(H p_x-p_x H\bigr) -\frac{i}{\hbar}\frac{e}{c}\left(H A_x -A_x H\right)-\frac{e}{c}\ppdiff{A_x}{t}\\
&=\frac{i}{\hbar}\left(e\phi p_x-p_x e\phi-e\mb{\alpha}\cdot\mb{A}p_x+p_x e\mb{\alpha}\cdot\mb{A}\right)
-\frac{i}{\hbar}\frac{e}{c}c\mb{\alpha}\cdot\mb{p}A_x-\frac{e}{c}\ppdiff{A_x}{t}\\
&=\frac{i}{\hbar}\left(-\frac{\hbar}{i}\pdiff{x}e\phi\right)+\frac{i}{\hbar}e\mb{\alpha}\cdot\left(\frac{\hbar}{i}\pdiff{x}\mb{A}\right)
-\frac{i}{\hbar}e\mb{\alpha}\cdot\left(\frac{\hbar}{i}\nabla A_x\right)-\frac{e}{c}\ppdiff{A_x}{t}\\
&=-e\ppdiff{\phi}{x}+e\mb{\alpha}\cdot\ppdiff{\mb{A}}{x}-e(\mb{\alpha}\cdot\nabla)A_x
-\frac{e}{c}\ppdiff{A_x}{t}
\end{align*}
\(\mb{A}\) と \(A_x\) 中の項は, 最後の項を除いて次のように展開される：
\begin{align*}
e\mb{\alpha}\cdot\ppdiff{\mb{A}}{x}-e(\mb{\alpha}\cdot\nabla)A_x
&=e\left(\alpha_1\ppdiff{A_x}{x}+\alpha_2\ppdiff{A_y}{x}+\alpha_3\ppdiff{A_z}{x}
-\alpha_1\pdiff{x}A_x-\alpha_2\pdiff{y}A_x-\alpha_3\pdiff{z}A_x\right)
\end{align*}
すると,
\begin{align*}
e\mb{\alpha}\cdot\ppdiff{\mb{A}}{x}-e(\mb{\alpha}\cdot\nabla)A_x
&=e\alpha_2\left(\ppdiff{A_y}{x}-\alpha_2\pdiff{y}A_x\right)
+e\alpha_3\left(\ppdiff{A_z}{x}-\pdiff{z}A_x\right)\\
&=e\alpha_2\bigl(\nabla\times\mb{A}\bigr)_{3}-\alpha_3\bigl(\nabla\times\mb{A}\bigr)_2\\
&=e\bigl\{\mb{\alpha}\times(\nabla\times\mb{A})\bigr\}_1
\end{align*}
従って, これは次の量の \(x\) 成分と見られる：
\begin{equation*}
e\mb{\alpha}\times(\nabla\times\mb{A})=e\mb{\alpha}\times\mb{B}
\end{equation*}
e\mb{\alpha}\times(\nabla\times\mb{A})=e\mb{\alpha}\times\mb{B}
\end{equation*}
この最初と最後の項は \(\mb{E}\) の \(x\) 成分となっている：
\begin{equation*}
-e\ppdiff{\phi}{x}-\frac{e}{c}\ppdiff{A_x}{t}=e\left(-\frac{1}{c}\ppdiff{A_x}{t}-\ppdiff{\phi}{x}\right)
=e\left(-\reverse{c}\ppdiff{\mb{A}}{t}-\nabla\phi\right)_x=eE_x
\end{equation*}
-e\ppdiff{\phi}{x}-\frac{e}{c}\ppdiff{A_x}{t}=e\left(-\frac{1}{c}\ppdiff{A_x}{t}-\ppdiff{\phi}{x}\right)
=e\left(-\reverse{c}\ppdiff{\mb{A}}{t}-\nabla\phi\right)_x=eE_x
\end{equation*}
以上の結果をまとめると次式が言える：
\begin{equation*}
\dot{\mb{\pi}}_{x}=eE_x +e\left(\mb{\alpha}\times\mb{B}\right)_x,
\quad\rightarrow\quad
\dot{\overline{\left(\mb{p}-\frac{e}{c}\mb{A}\right)}}\equiv \frac{d}{dt}\left(\mb{p}-\frac{e}{c}\mb{A}\right)
=e\bigl(\mb{E}+\mb{\alpha}\times\mb{B}\bigr)=\mb{F}
\end{equation*}
\dot{\mb{\pi}}_{x}=eE_x +e\left(\mb{\alpha}\times\mb{B}\right)_x,
\quad\rightarrow\quad
\dot{\overline{\left(\mb{p}-\frac{e}{c}\mb{A}\right)}}\equiv \frac{d}{dt}\left(\mb{p}-\frac{e}{c}\mb{A}\right)
=e\bigl(\mb{E}+\mb{\alpha}\times\mb{B}\bigr)=\mb{F}
\end{equation*}
ただし \(\mb{F}\) はローレンツ力に類似した量である．この方程式はときどきニュートンの運動方程式の類似物と見做される．しかし, この方程式と \(\dot{\mb{x}}\) との直接的な関係は存在しないので, 速度を小さくした極限で直にニュートン方程式とはならない．従って,「この方程式は適切な類似式だ」と完全に認めることは出来ない．
以下の関係式は真であることを証明できるが, それらの意味はまだ完全には理解されていない：
\begin{align}
&\frac{d}{dt}\left(\mb{x}+\frac{i\hbar}{2mc}\beta\mb{\alpha}\right)
=\frac{\beta}{m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)\tag{1}\\
&\frac{d}{dt}\left(ct+\frac{i\hbar}{2mc}\beta\right)
=\frac{\beta}{mc}\bigl(H-e\phi\bigr)\tag{2}\\
&i\frac{d}{dt}\alpha_x\alpha_y\alpha_z
=-\frac{2mc^{2}}{\hbar}\beta\,\alpha_x\alpha_y\alpha_z\tag{3}\\
&-\frac{d}{dt}\beta\,\mb{\Sigma}
=\frac{2c}{\hbar}\bigl(\beta\,\alpha_x\alpha_y\alpha_z\bigr)\left(\mb{p}-\frac{e}{c}\mb{A}\right)\tag{4}
\end{align}
&\frac{d}{dt}\left(\mb{x}+\frac{i\hbar}{2mc}\beta\mb{\alpha}\right)
=\frac{\beta}{m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)\tag{1}\\
&\frac{d}{dt}\left(ct+\frac{i\hbar}{2mc}\beta\right)
=\frac{\beta}{mc}\bigl(H-e\phi\bigr)\tag{2}\\
&i\frac{d}{dt}\alpha_x\alpha_y\alpha_z
=-\frac{2mc^{2}}{\hbar}\beta\,\alpha_x\alpha_y\alpha_z\tag{3}\\
&-\frac{d}{dt}\beta\,\mb{\Sigma}
=\frac{2c}{\hbar}\bigl(\beta\,\alpha_x\alpha_y\alpha_z\bigr)\left(\mb{p}-\frac{e}{c}\mb{A}\right)\tag{4}
\end{align}
ただし最後の関係式中の \(\mb{\Sigma}\) は, 次の行列を意味している：
\begin{equation*}
\mb{\Sigma}\equiv \begin{pmatrix}
\mb{\sigma} & 0 \\ 0 & \mb{\sigma}
\end{pmatrix},\quad\rightarrow \quad \Sigma_z =-i\alpha_x\alpha_y,\quad \mathrm{etc.}
\end{equation*}
\mb{\Sigma}\equiv \begin{pmatrix}
\mb{\sigma} & 0 \\ 0 & \mb{\sigma}
\end{pmatrix},\quad\rightarrow \quad \Sigma_z =-i\alpha_x\alpha_y,\quad \mathrm{etc.}
\end{equation*}
〈 導出例 〉 (1) ハミルトニアン \(H=\beta mc^{2}+e\phi+c\mb{\alpha}\cdot\mb{\pi}\) と \(\beta\mb{\alpha}\) との交換子を, \(\alpha_i\) や \(\beta\) の交換関係
\begin{equation*}
\alpha_i\alpha_j+\alpha_j\alpha_i=2\delta_{ij},\quad \beta^{2}=1,\quad \beta\mb{\alpha}+\mb{\alpha}\beta=0
\end{equation*}
\alpha_i\alpha_j+\alpha_j\alpha_i=2\delta_{ij},\quad \beta^{2}=1,\quad \beta\mb{\alpha}+\mb{\alpha}\beta=0
\end{equation*}
を用いて具体的に計算してみると (ただし \(\mb{\pi}=\mb{p}-(e/c)\mb{A}\) とした),
\begin{align*}
[H,\beta\mb{\alpha}]&=mc^{2}\bigl(\beta\beta\mb{\alpha}-\beta\mb{\alpha}\beta\bigr)
+c\bigl(\mb{\alpha}\cdot\mb{\pi}\beta\mb{\alpha}-\beta\mb{\alpha}\mb{\alpha}\cdot\mb{\pi}\bigr),\\
\bigl(\beta\beta\mb{\alpha}-\beta\mb{\alpha}\beta\bigr)&=\mb{\alpha}+\beta\beta\mb{\alpha}=2\mb{\alpha},\\
\mb{\alpha}\cdot\mb{\pi}\beta\mb{\alpha}\to \pi_k\alpha_k\beta\alpha_i
&=\pi_k (-\beta\alpha_k)\alpha_i=\pi_k(-\beta)\bigl(-\alpha_i\alpha_k+2\delta_{ki}\bigr)\\
&=\pi_k\beta\alpha_i\alpha_k-2\pi_k\beta\delta_{ki}
=\beta\alpha_i\mb{\alpha}\cdot\mb{\pi}-2\beta\pi_i
\to \beta\mb{\alpha}\mb{\alpha}\cdot\mb{\pi}-2\beta\mb{\pi}\\
\therefore\quad \mb{\alpha}\cdot\mb{\pi}\beta\mb{\alpha}-\beta\mb{\alpha}\mb{\alpha}\cdot\mb{\pi}
&=\beta\mb{\alpha}\mb{\alpha}\cdot\mb{\pi}-2\beta\mb{\pi}-\beta\mb{\alpha}\mb{\alpha}\cdot\mb{\pi}
=-2\beta\mb{\pi}\\
\Rightarrow\quad [H,\beta\mb{\alpha}]
&=mc^{2}\bigl(\beta\beta\mb{\alpha}-\beta\mb{\alpha}\beta\bigr)
+c\bigl(\mb{\alpha}\cdot\mb{\pi}\beta\mb{\alpha}-\beta\mb{\alpha}\mb{\alpha}\cdot\mb{\pi}\bigr)\\
&=2mc^{2}\mb{\alpha}-2c\beta\mb{\pi}\\
\therefore\quad \frac{d}{dt}\left(\mb{x}+\frac{i\hbar}{2mc}\beta\mb{\alpha}\right)
&=c\mb{\alpha}+\frac{i\hbar}{2mc}\frac{d}{dt}\beta\mb{\alpha}
=c\mb{\alpha}+\frac{i\hbar}{2mc}\frac{i}{\hbar}[H,\beta\mb{\alpha}]\\
&=c\mb{\alpha}-\frac{1}{2mc}[H,\beta\mb{\alpha}]
=c\mb{\alpha}-\frac{1}{2mc}(2mc^{2}\mb{\alpha}-2c\beta\mb{\pi})\\
&=c\mb{\alpha}-c\mb{\alpha}+\frac{\beta}{mc}\mb{\pi}
=\frac{\beta}{mc}\mb{\pi}
\end{align*}
同様にして (2) は \(c\mb{\alpha}\cdot\mb{\pi}=H-e\phi-\beta mc^{2}\) より,
\begin{align*}
[H,\beta]&=(c\alpha_k\pi_k + \beta mc^{2}+e\phi)\beta-\beta(c\alpha_k\pi_k + \beta mc^{2}+e\phi)\\
&=c\pi_k\alpha_k\beta-c\pi_k\beta\alpha_k+\beta^{2}mc^{2}-\beta^{2}mc^{2}
=-c\pi_k\beta\alpha_k-c\pi_k\beta\alpha_k\\
&=-2c\beta\alpha_k\pi_k =-2\beta\,c\mb{\alpha}\cdot\mb{\pi}
=-2\beta\bigl(H-e\phi-\beta mc^{2}\bigr)
=-2\beta\bigl(H-e\phi\bigr)+2mc^{2}\\
\therefore\quad \frac{d}{dt}\left(ct+\frac{i\hbar}{2mc}\beta\right)
&=c+\frac{i\hbar}{2mc}\dot{\beta}
=c+\frac{i\hbar}{2mc}\frac{i}{\hbar}[H,\beta]=c-\frac{1}{2mc}[H,\beta]\\
&=c-\frac{1}{2mc}\times\left\{-2\beta\bigl(H-e\phi\bigr)+2mc^{2}\right\}
=c+\frac{\beta}{mc}(H-e\phi)-c\\
&=\frac{\beta}{mc}(H-e\phi)
\end{align*}
同様にして (3) は,
\begin{align*}
[H,\alpha_1\alpha_2\alpha_3]
&=(c\alpha_k\pi_k + \beta mc^{2}+e\phi)\alpha_1\alpha_2\alpha_3-\alpha_1\alpha_2\alpha_3(c\alpha_k\pi_k + \beta mc^{2}+e\phi)\\
&=c\pi_k\bigl(\alpha_k\alpha_1\alpha_2\alpha_3-\alpha_1\alpha_2\alpha_3\alpha_k\bigr)
+ mc^{2}\bigl(\beta\alpha_1\alpha_2\alpha_3-\alpha_1\alpha_2\alpha_3\beta\bigr),\\
\alpha_k\alpha_1\alpha_2\alpha_3&=(-\alpha_1\alpha_k+2\delta_{k1})\alpha_2\alpha_3=-\alpha_1\alpha_k\alpha_2\alpha_3+2\delta_{k1}\alpha_2\alpha_3=\dotsb\\
&= -\alpha_1\alpha_2\alpha_3\alpha_k+2\alpha_1\alpha_2\delta_{3k}+2\alpha_3\alpha_1\delta_{2k}+2\alpha_2\alpha_3\delta_{1k}\\
\rightarrow \quad c\pi_k\bigl(\alpha_k\alpha_1\alpha_2\alpha_3-\alpha_1\alpha_2\alpha_3\alpha_k\bigr)
&=c\pi_k\bigl(-\alpha_1\alpha_2\alpha_3\alpha_k+2\alpha_1\alpha_2\delta_{3k}+2\alpha_3\alpha_1\delta_{2k}+2\alpha_2\alpha_3\delta_{1k}-\alpha_1\alpha_2\alpha_3\alpha_k\bigr)\\
&=2c\bigl(\alpha_1\alpha_2\pi_3+\alpha_3\alpha_1\pi_2+\alpha_2\alpha_3\pi_1\bigr)-2c\alpha_1\alpha_2\alpha_3\alpha_k\pi_k\\
&=2c\bigl(\alpha_1\alpha_2\alpha_3\alpha_3\pi_3+\alpha_3\alpha_1\alpha_2\alpha_2\pi_2+\alpha_2\alpha_3\alpha_1\alpha_1\pi_1\bigr)
-2c\alpha_1\alpha_2\alpha_3\alpha_k\pi_k\\
&=2c\alpha_1\alpha_2\alpha_3\alpha_k\pi_k-2c\alpha_1\alpha_2\alpha_3\alpha_k\pi_k=0,\\
\alpha_1\alpha_2\alpha_3\beta&=-\alpha_1\alpha_2\beta\alpha_3=+\alpha_1\beta\alpha_2\alpha_3=-\beta\alpha_1\alpha_2\alpha_3,\\
\rightarrow \quad mc^{2}\bigl(\beta\alpha_1\alpha_2\alpha_3-\alpha_1\alpha_2\alpha_3\beta\bigr)
&=mc^{2}(\beta\alpha_1\alpha_2\alpha_3+\beta\alpha_1\alpha_2\alpha_3)=2mc^{2}\beta\alpha_1\alpha_2\alpha_3,\\
\therefore\quad i\frac{d}{dt}\alpha_1\alpha_2\alpha_3 &=i\times\frac{i}{\hbar}[H,\alpha_1\alpha_2\alpha_3]
=\frac{-1}{\hbar}\times 2mc^{2}\beta\alpha_1\alpha_2\alpha_3=-\frac{2mc^{2}}{\hbar}\beta \alpha_1\alpha_2\alpha_3
\end{align*}
式 (4) については, 行列 \(\mb{\Sigma}\) は \(\gamma\) 行列を用いて表せること, また \(\mb{\alpha}=\beta\mb{\gamma}\) の関係から \(\beta\,\mb{\Sigma}\) は \(\alpha_i,\beta\) を用いて表わせることを利用する：
\begin{equation*}
\mb{\Sigma}=\bigl(i\gamma^{2}\gamma^{3},\,i\gamma^{3}\gamma^{1},\,i\gamma^{1}\gamma^{2}\bigr),\quad
\beta\,\mb{\Sigma}=\bigl(-i\beta\alpha_2\alpha_3,\,-i\beta\alpha_3\alpha_1,\,-i\beta\alpha_1\alpha_2,\bigr)
\end{equation*}
\mb{\Sigma}=\bigl(i\gamma^{2}\gamma^{3},\,i\gamma^{3}\gamma^{1},\,i\gamma^{1}\gamma^{2}\bigr),\quad
\beta\,\mb{\Sigma}=\bigl(-i\beta\alpha_2\alpha_3,\,-i\beta\alpha_3\alpha_1,\,-i\beta\alpha_1\alpha_2,\bigr)
\end{equation*}
そこで例えば, 交換子 \([H,\beta\,\Sigma_1]\) 即ち \([H,\beta\alpha_2\alpha_3]\) を具体的に計算してみる：
\begin{align*}
[H,\beta\,\alpha_2\alpha_3]
&=\bigl(c\alpha_k\pi_k + \beta mc^{2}+e\phi\bigr)\beta\alpha_2\alpha_3
-\beta\alpha_2\alpha_3\bigl(c\alpha_k\pi_k + \beta mc^{2}+e\phi\bigr)\\
&=mc^{2}\bigl(\beta\beta\alpha_2\alpha_3-\beta\alpha_2\alpha_3\beta\bigr)
+c\bigl(\pi_k\alpha_k\beta\alpha_2\alpha_3-\beta\alpha_2\alpha_3\alpha_k\pi_k\bigr)
\end{align*}
このとき,
\begin{align*}
\beta\beta\alpha_2\alpha_3-\beta\alpha_2\alpha_3\beta&=\alpha_2\alpha_3-\alpha_2\alpha_3\beta^{2}=0,\\
\pi_k\alpha_k\beta\alpha_2\alpha_3-\beta\alpha_2\alpha_3\alpha_k\pi_k
&=\bigl(\alpha_1\pi_1+\alpha_2\pi_2+\alpha_3\pi_3\bigr)\beta\alpha_2\alpha_3-\beta\alpha_2\alpha_3\bigl(\alpha_1\pi_1+\alpha_2\pi_2+\alpha_3\pi_3\bigr)\\
&=\pi_1(-\beta)\alpha_1\alpha_2\alpha_3-\pi_2\beta\alpha_3+\pi_3\beta\alpha_2-\pi_1\beta\alpha_1\alpha_2\alpha_3
+\pi_2\beta\alpha_3-\pi_3\beta\alpha_2\\
&=-2\pi_1\beta\alpha_1\alpha_2\alpha_3
\end{align*}
従って,
\begin{align*}
[H,\beta\,\alpha_2\alpha_3]&=-2c\beta\alpha_1\alpha_2\alpha_3\pi_1,\\
\therefore\quad \frac{d}{dt}\beta\Sigma_1&=\frac{i}{\hbar}[H,-i\beta\,\alpha_2\alpha_3]
=\frac{i}{\hbar}\times(-i)\times (-2c\beta\alpha_1\alpha_2\alpha_3\pi_1)
=-\frac{2c}{\hbar}\beta \alpha_1\alpha_2\alpha_3\pi_1,\\
\rightarrow\quad \frac{d}{dt}\beta\mb{\Sigma}&=-\frac{2c}{\hbar}\beta\alpha_1\alpha_2\alpha_3\mb{\pi},\quad\mathrm{or}
\quad -\frac{d}{dt}\beta\Sigma=\frac{2c}{\hbar}\beta\alpha_1\alpha_2\alpha_3\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\end{align*}
古典物理の類似式から, 角運動量演算子は今や次式となると期待出来る：
\begin{equation*}
\mb{L}=\mb{R}\times\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\end{equation*}
\mb{L}=\mb{R}\times\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\end{equation*}
古典物理学では次式となることに注意する：
\begin{equation*}
\mb{p}-\frac{e}{c}\mb{A}=\frac{m\mb{v}}{\sqrt{\ds{1-\frac{v^{2}}{c^{2}}}}}
\end{equation*}
\mb{p}-\frac{e}{c}\mb{A}=\frac{m\mb{v}}{\sqrt{\ds{1-\frac{v^{2}}{c^{2}}}}}
\end{equation*}
前述した \(\dot{R}\) と \(\dot{\overline{\mb{p}-(e/c)\mb{A}}}\) の結果から, 角運動量 \(\mb{L}\) の時間微分は次のように書ける：
\begin{align*}
\dot{\mb{L}}&=\dot{\mb{R}}\times \left(\mb{p}-\frac{e}{c}\mb{A}\right)
+\mb{R}\times\dot{\overline{\left(\mb{p}-\frac{e}{c}\mb{A}\right)}}\\
&=c\mb{\alpha}\times \left(\mb{p}-\frac{e}{c}\mb{A}\right)
+\mb{R}\times\mb{F}
\end{align*}
この最後の項は「トルク」と解釈することが出来る．\(\mb{F}\) が中心力の場合, この項はゼロとなる．しかしその場合, 最初の項があるために \(\dot{\mb{L}}\ne0\) であることが分かる．すなわち, 中心力の場合でも角運動量 \(\mb{L}\)は「保存されない」．
しかしながら, 次で定義される演算子 \(\mb{\Sigma}\) の時間微分を考えてみよう：
\begin{equation*}
\mb{\Sigma}=\begin{pmatrix} \mb{\sigma} & 0 \\ 0 & \mb{\sigma} \end{pmatrix},\quad \mathrm{where}\quad
\Sigma_3=i\gamma^{1}\gamma^{2}=-i\alpha_1\alpha_2,\ \mathrm{etc}
\end{equation*}
\mb{\Sigma}=\begin{pmatrix} \mb{\sigma} & 0 \\ 0 & \mb{\sigma} \end{pmatrix},\quad \mathrm{where}\quad
\Sigma_3=i\gamma^{1}\gamma^{2}=-i\alpha_1\alpha_2,\ \mathrm{etc}
\end{equation*}
\(z\) 成分は \(\beta\) と \(e\phi\) そして \(H\) 中の \(\alpha_3\) 項とは交換するが \(H\) 中の \(\alpha_1\) 項と \(\alpha_2\) 項とは交換しないことが分かる．従って \(\displaystyle \mb{\pi}=\mb{p}-\frac{e}{c}\mb{A}\) とするとき,
\begin{align*}
\frac{d}{dt}\Sigma_3=\dot{\Sigma}_3&=\frac{i}{\hbar}[H,\Sigma_3]=\frac{i}{\hbar}[H,-i\alpha_1\alpha_2]=\frac{1}{\hbar}[H,\alpha_1\alpha_2]
=\frac{1}{\hbar}\bigl(H\alpha_1\alpha_2-\alpha_1\alpha_2 H\bigr)\\
&=\frac{1}{\hbar}\left\{\left(\beta mc^{2}+e\phi+c\mb{\alpha}\cdot\mb{\pi}\right)\alpha_1\alpha_2-
\alpha_1\alpha_2\left(\beta mc^{2}+e\phi+c\mb{\alpha}\cdot\mb{\pi}\right)\right\}\\
&=\frac{1}{\hbar}\bigl\{c\mb{\alpha}\cdot\mb{\pi}\alpha_1\alpha_1-\alpha_1\alpha_1c\mb{\alpha}\cdot\mb{\pi}\bigr\}
=\frac{c}{\hbar}\sum_k \bigl(\alpha_k\pi_k\alpha_1\alpha_2-\alpha_1\alpha_2\alpha_k\pi_k\bigr)\\
&=\frac{c}{\hbar}\sum_k \pi_k\bigl(\alpha_k\alpha_1\alpha_2-\alpha_1\alpha_2\alpha_k\bigr)\\
\alpha_1\alpha_2\alpha_k&=\alpha_1\bigl(-\alpha_k\alpha_2+2\delta_{k2}\bigr)
=-\alpha_1\alpha_k\alpha_2 +2\delta_{k2}\alpha_1\\
&=-\bigl(-\alpha_k\alpha_1+2\delta_{k1}\alpha_2+2\delta_{k2}\alpha_1\bigr)
=\alpha_k\alpha_1\alpha_2-2\delta_{1k}\alpha_2 + 2\delta_{k2}\alpha_1,\\
\rightarrow\quad\sum_k &\pi_k\bigl(\alpha_k\alpha_1\alpha_2-\alpha_1\alpha_2\alpha_k\bigr)
=\sum_k \pi_k\bigl(\alpha_k\alpha_1\alpha_2-\alpha_k\alpha_1\alpha_2+2\delta_{1k}\alpha_2 – 2\delta_{k2}\alpha_1\bigr)\\
&=2\sum_k \pi_k\alpha_2\delta_{1k}-2\sum_k \pi_k\alpha_1\delta_{k2}
=2\alpha_2\pi_1-2\alpha_1\pi_2=-2\bigl(\alpha_1\pi_2-\alpha_2\pi_1\bigr)
\end{align*}
従って,
\begin{equation*}
\dot{\Sigma}_3 =-\frac{2c}{\hbar}\bigl(\alpha_1\pi_2-\alpha_2\pi_1\bigr)
= -\frac{2c}{\hbar}\bigl(\mb{\alpha}\times\mb{\pi}\bigr)_3
\end{equation*}
\dot{\Sigma}_3 =-\frac{2c}{\hbar}\bigl(\alpha_1\pi_2-\alpha_2\pi_1\bigr)
= -\frac{2c}{\hbar}\bigl(\mb{\alpha}\times\mb{\pi}\bigr)_3
\end{equation*}
よって最終的に,
\begin{equation*}
\frac{\hbar}{2}\dot{\mb{\Sigma}}=-c\mb{\alpha}\times\mb{\pi}=-c\mb{\alpha}\times\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\end{equation*}
\frac{\hbar}{2}\dot{\mb{\Sigma}}=-c\mb{\alpha}\times\mb{\pi}=-c\mb{\alpha}\times\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\end{equation*}
これは \(\dot{\mb{L}}\) にマイナス符号を付けたものの最初の項である．従って,
\begin{equation*}
\frac{d}{dt}\left[\mb{L}+\frac{\hbar}{2}\mb{\Sigma}\right]=\mb{R}\times\mb{F}
\end{equation*}
\frac{d}{dt}\left[\mb{L}+\frac{\hbar}{2}\mb{\Sigma}\right]=\mb{R}\times\mb{F}
\end{equation*}
が導かれる．これは中心力の場合, ゼロになる．演算子 \(\displaystyle \mb{L}+\frac{\hbar}{2}\mb{\Sigma}\) は「全角運動量演算子」と見做すことが出来る．ただし \(\mb{L}\) は軌道角運動量であり \((\hbar/2)\mb{\Sigma}\) はスピン \(1/2\) の「固有角運動量」(intrinsic angular momentum) である．従って,「中心力の場合には, 全角運動量は保存される」．
【 問題 】 (1) 静的な場 \(\phi=0,\partial \mb{A}/\partial t =0\) の場合には, 次の量は「運動の定数」(constant of the motion) であることを示せ：
\begin{equation*}
\mb{\Sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\end{equation*}
\mb{\Sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\end{equation*}
これは, 電子の「異常磁気回転比」(anomalous gyromagnetic ratio) [5][ブログ註] 荷電粒子が円運動を行えば, … Continue reading の結果であることに注意する．それはまた,「電子のサイクロトロン周波数は, 磁場中に於けるその歳差比に等しい」ことも意味している．
(2) 静的な磁場 \(\phi=0,\partial \mb{A}/\partial t=0\) の場合, そして静的状態の場合には, \(\psi=(\psi_1,\psi_2,\psi_3,\psi_4)^{t}\) 中の \(\psi_1,\psi_2\) は, パウリ方程式中の \(\psi_1,\psi_2\) と同じであることを示せ．また, パウリ方程式中の運動エネルギーを \(E_{\mathrm{Pauli}}\) とし, デイラック方程式中の静止エネルギーと運動エネルギーの和を \(E_{\mathrm{Dirac}}=W+mc^{2}\) とするならば, 次式が言えることを示せ：
\begin{equation*}
E_{\mathrm{Dirac}}=\sqrt{2mc^{2} E_{\mathrm{Pauli}} +m^{2}c^{4}}
\end{equation*}
E_{\mathrm{Dirac}}=\sqrt{2mc^{2} E_{\mathrm{Pauli}} +m^{2}c^{4}}
\end{equation*}
そして, この関係式の簡便さを説明せよ．
〈 解答例 〉 (1) \(\displaystyle\ \mb{\pi}=\mb{p}-\frac{e}{c}\mb{A}\) として, 電磁場中の電子の \(\mb{\Sigma}\cdot\mb{\pi}\) の時間依存性を考える．ハミルトニアンを式 (11-2) とする：
\begin{equation*}
H=c\mb{\alpha}\cdot\mb{\pi}+e\phi+\beta mc^2
=c\gamma^{5}\mb{\Sigma}\cdot\mb{\pi}+e\phi+\beta mc^2
\tag{1}
\end{equation*}
H=c\mb{\alpha}\cdot\mb{\pi}+e\phi+\beta mc^2
=c\gamma^{5}\mb{\Sigma}\cdot\mb{\pi}+e\phi+\beta mc^2
\tag{1}
\end{equation*}
ただし, 上式では「一般化スピン」 \(\mb{\Sigma}\) と \(\mb{\alpha}\) に次のような関係が成り立つことを利用して変形している：
\begin{equation*}
\alpha_{k}=\Sigma_{k}\gamma^{5}=\gamma^{5}\Sigma_{k}
=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}
\begin{pmatrix} \sigma_{k} & 0 \\ 0 & \sigma_{k} \end{pmatrix}
=\begin{pmatrix} 0 & \sigma_{k} \\ \sigma_{k} & 0 \end{pmatrix},\quad\rightarrow\quad
\mb{\alpha}=\gamma^{5}\mb{\Sigma}=\mb{\Sigma}\gamma^{5}
\tag{2}
\end{equation*}
\alpha_{k}=\Sigma_{k}\gamma^{5}=\gamma^{5}\Sigma_{k}
=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}
\begin{pmatrix} \sigma_{k} & 0 \\ 0 & \sigma_{k} \end{pmatrix}
=\begin{pmatrix} 0 & \sigma_{k} \\ \sigma_{k} & 0 \end{pmatrix},\quad\rightarrow\quad
\mb{\alpha}=\gamma^{5}\mb{\Sigma}=\mb{\Sigma}\gamma^{5}
\tag{2}
\end{equation*}
このとき, 行列 \(\gamma^{5}\) と \(\Sigma_k\) とは交換することに注意する．
演算子 \(\mb{\Sigma}\cdot\mb{\pi}\) に対するハイゼンベルグの運動方程式は次となる：
\begin{align*}
\frac{d\mb{\Sigma}\cdot\mb{\pi}}{dt}&=\frac{i}{\hbar}\bigl[H,\mb{\Sigma}\cdot\mb{\pi}\bigr]
=\frac{i}{\hbar}\bigl[c\gamma^{5}\mb{\Sigma}\cdot\mb{\pi}+e\phi+\beta mc^2, \,\mb{\Sigma}\cdot\mb{\pi}\bigr]\\
&=\frac{ic}{\hbar}\bigl[\gamma^{5}\mb{\Sigma}\cdot\mb{\pi},\,\mb{\Sigma}\cdot\mb{\pi}\bigr]
+\frac{ie}{\hbar}\bigl[\phi,\mb{\Sigma}\cdot\mb{\pi}\bigr]+\frac{imc^{2}}{\hbar}\bigl[\beta, \,\mb{\Sigma}\cdot\mb{\pi}\bigr]\\
&=\frac{ie}{\hbar}\bigl[\phi,\mb{\Sigma}\cdot\mb{\pi}\bigr]
\tag{3}
\end{align*}
ただし, 上式では \(\gamma^{5}\) と \(\beta\) が \(\mb{\Sigma}\cdot\mb{\pi}\) と可換であることを用いている：
\begin{align*}
\beta\,\Sigma_k&=\gamma^{0}\Sigma_k=\Sigma_k\gamma^{0}=\Sigma_k\,\beta=\begin{pmatrix} \sigma_{k} & 0 \\ 0 & -\sigma_{k} \end{pmatrix},\qquad
\gamma^{5}\mb{\Sigma}=\mb{\Sigma}\gamma^{5}=\begin{pmatrix} 0 & \mb{\sigma} \\ \mb{\sigma} & 0 \end{pmatrix},\\
\rightarrow\quad &\bigl[\gamma^{5}\mb{\Sigma}\cdot\mb{\pi},\,\mb{\Sigma}\cdot\mb{\pi}\bigr]
=\gamma^{5}\mb{\Sigma}\cdot\mb{\pi}\,\mb{\Sigma}\cdot\mb{\pi}-\mb{\Sigma}\cdot\mb{\pi}\,\gamma^{5}\mb{\Sigma}\cdot\mb{\pi}
=\gamma^{5}\mb{\Sigma}\cdot\mb{\pi}\,\mb{\Sigma}\cdot\mb{\pi}-\gamma^{5}\mb{\Sigma}\cdot\mb{\pi}\,\mb{\Sigma}\cdot\mb{\pi}=0,\\
&\bigl[\beta,\,\mb{\Sigma}\cdot\mb{\pi}\bigr]=\bigl[\beta,\Sigma_k\pi_k\bigr]
=\pi_k\bigl[\beta,\Sigma_k\bigr]=0
\end{align*}
ここで, 次の交換関係が成り立つ：
\begin{align*}
\bigl[\phi,\pi_k\bigr]&=\phi\left(\frac{\hbar}{i}\pdiff{x_k}\right)-\left(\frac{\hbar}{i}\pdiff{x_k}\right)\phi
=\phi\left(\frac{\hbar}{i}\pdiff{x_k}\right)-\frac{\hbar}{i}\ppdiff{\phi}{x_k}-\phi\left(\frac{\hbar}{i}\pdiff{x_k}\right)\\
&=-\frac{\hbar}{i}\ppdiff{\phi}{x_k}=i\hbar \ppdiff{\phi}{x_k}
\tag{4}
\end{align*}
従って, 式 (3) は次となる：
\begin{align*}
\frac{d\mb{\Sigma}\cdot\mb{\pi}}{dt}&=\frac{ie}{\hbar}\bigl[\phi,\mb{\Sigma}\cdot\mb{\pi}\bigr]
=\frac{ie}{\hbar}\bigl[\phi,\Sigma_k\,\pi_k\bigr]=\frac{ie}{\hbar}\Sigma_k\,\bigl[\phi,\pi_k\bigr]
=\frac{ie}{\hbar}\Sigma_k\times i\hbar\ppdiff{\phi}{x_k}\\
&=-e\Sigma_k\pdiff{x_k}\phi=-e\mb{\Sigma}\cdot\nabla\phi=e\mb{\Sigma}\cdot\left(-\nabla\phi\right)
\tag{5}
\end{align*}
静的な場を仮定しているから \(A^{\mu}=(\phi,\mb{A})\) は時間に依存しない．従って,
\begin{equation*}
\ppdiff{\phi}{t}=0,\quad \ppdiff{\mb{A}}{t}=0,\quad\rightarrow\quad
\mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t}-\nabla\phi=-\nabla\phi
\end{equation*}
\ppdiff{\phi}{t}=0,\quad \ppdiff{\mb{A}}{t}=0,\quad\rightarrow\quad
\mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t}-\nabla\phi=-\nabla\phi
\end{equation*}
よって式 (5) は,
\begin{equation*}
\frac{d\mb{\Sigma}\cdot\mb{\pi}}{dt}=e\mb{\Sigma}\cdot\left(-\nabla\phi\right)
=e\mb{\Sigma}\cdot\mb{E}
\tag{6}
\end{equation*}
\frac{d\mb{\Sigma}\cdot\mb{\pi}}{dt}=e\mb{\Sigma}\cdot\left(-\nabla\phi\right)
=e\mb{\Sigma}\cdot\mb{E}
\tag{6}
\end{equation*}
さらに, 電場が無い状況 \((\mb{E}=0)\) すなわち \(\phi=0\) を想定してみよう．すると,
\begin{equation*}
\frac{d\,\mb{\Sigma}\cdot\mb{\pi}}{dt}=0
\tag{7}
\end{equation*}
\frac{d\,\mb{\Sigma}\cdot\mb{\pi}}{dt}=0
\tag{7}
\end{equation*}
よって \(\mb{\Sigma}\cdot\mb{\pi}\) は, 時間に依存しないで一定に保たれる, 即ち「運動の定数」となることが分かる．
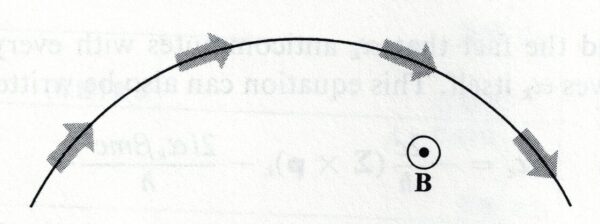
「時間に依存しない磁場中では, 荷電粒子の「力学的運動量 \(\mb{\pi}\) の大きさ」は変化しないことが分かっている．\(\mb{\Sigma}\cdot\mb{\pi}\) が一定であるということは,「ヘリシティが一定である」ということである [6][ブログ註] 運動量 \(\mb{p}\) の向きの単位ベクトル \(\hat{\mb{p}}=\mb{p}/|\mb{p}|\) と一般化スピン \(\mb{\Sigma}\) との内積を「ヘリシティ演算子」(helicity … Continue reading．
従って, 磁場のある領域に入った縦偏極電子 (ヘリシティが \(+1\) または \(-1\)) すなわち「そのスピンが運動量方向を向いている電子」は, 磁場 \(\mb{B}\) がどんなに複雑であっても縦偏極のままである．電子がその初速度と垂直な方向に一様磁場 \(\mb{B}\) が存在する領域に入射されるとき, 電子は円軌道をたどるが, その角周波数は「サイクロトロン周波数」として知られいる：[7][ブログ註] (ランダウ §48 より) 一様な磁場 \(\mb{H}\) の中での電荷 \(e\) の運動を考える．磁場の方向を \(z\) 軸にとる．運動方程式 \(\displaystyle … Continue reading
\begin{equation}
\omega_{L}=\frac{|e\mb{B}|}{mc}\sqrt{1-\beta^{2}}
\tag{8}
\end{equation}
\omega_{L}=\frac{|e\mb{B}|}{mc}\sqrt{1-\beta^{2}}
\tag{8}
\end{equation}
この特に単純な場合では,「ヘリシティが一定であること」は, 下図 3-5 に絵で示したように,「電子スピンは,その歳差角周波数 \(\omega_S\) が \(\omega_L\) に等しくなるように歳差運動する」ことを意味している．
図 3-5. 一様磁場中を移動する電子のスピン歳差運動．灰色の矢はスピン方向を示している．
\(\omega_L\) が \(\omega_S\) に等しいという式を導く際に, 我々は暗黙のうちに電子の磁気回転比が厳密に \(2\) であると仮定した．しかし実際には, 電子の異常磁気モーメントのために, 必ずしも \(\omega_L\) が \(\omega_S\) に等しいという訳ではない．正しい関係は次式で与えられることを示すことが出来る：
\begin{equation*}
\frac{\omega_S}{\omega_L}=1+\left(\frac{g-2}{2}\right)\frac{1}{\sqrt{1-\beta^{2}}}
\tag{9}
\end{equation*}
\frac{\omega_S}{\omega_L}=1+\left(\frac{g-2}{2}\right)\frac{1}{\sqrt{1-\beta^{2}}}
\tag{9}
\end{equation*}
この式が意味するのは,「最初に縦方向に偏極した電子が軌道を 1 回転すると, スピンの向きが運動方向からごく僅かだけずれる, 電子が非相対論的であれば \(1/137\) ラジアンだけずれる」と言うことである．この原理を用いることで, 電子とミューオンの異常磁気モーメントを精密に測定する実験が行われている．(J.J.Sakuraiの§3-6を参照した)．
(2) Diracスピノル \(\psi\) を式 (9-6) にあるように 2 成分 \(\psi_a,\psi_b\) で表し, また \(\mb{\gamma}\) 行列を \(2\times2\) 成分のパウリ行列 \(\mb{\sigma}\) で表わすと,
\begin{equation*}
\psi=\begin{pmatrix} \psi_a \\ \psi_b \end{pmatrix},\quad
\gamma^{0}=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix},\quad
\mb{\gamma}=\begin{pmatrix} 0 & \mb{\sigma} \\ -\mb{\sigma} & 0 \end{pmatrix}
\end{equation*}
\psi=\begin{pmatrix} \psi_a \\ \psi_b \end{pmatrix},\quad
\gamma^{0}=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix},\quad
\mb{\gamma}=\begin{pmatrix} 0 & \mb{\sigma} \\ -\mb{\sigma} & 0 \end{pmatrix}
\end{equation*}
これらを用いて Dirac方程式 (10-22) を具体的に書くと式 (9-6) のようになる：
\begin{align*}
\gamma^{\mu}\pi_{\mu}\psi=\pi_{\mu}\gamma^{\mu}\psi&=\pi_0\gamma^{0}\psi-\mb{\pi}\cdot\mb{\gamma}\psi=mc\psi,\\
\pi_0 \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\begin{pmatrix} \psi_a \\ \psi_b \end{pmatrix}
-\mb{\pi}\cdot \begin{pmatrix} 0 & \mb{\sigma} \\ -\mb{\sigma} & 0 \end{pmatrix}
&\begin{pmatrix} \psi_a \\ \psi_b \end{pmatrix}
= mc \begin{pmatrix} \psi_a \\ \psi_b \end{pmatrix}\quad \rightarrow\quad
\pi_0\begin{pmatrix} \psi_a \\ -\psi_b \end{pmatrix}-\mb{\pi}\cdot\begin{pmatrix} \mb{\sigma}\psi_b \\ -\mb{\sigma}\psi_a \end{pmatrix}
=mc\begin{pmatrix} \psi_a \\ \psi_b \end{pmatrix},\\
\therefore\quad \begin{cases} \pi_0\psi_a -\mb{\pi}\cdot\mb{\sigma}\psi_b=mc\psi_a \\
-\pi_0\psi_b +\mb{\pi}\cdot\mb{\sigma}\psi_a = mc\psi_b \end{cases}
&\quad\rightarrow\quad
\begin{cases}
\left(\ds{p_0-\frac{e}{c}\phi}\right)\psi_a-\mb{\sigma}\cdot\left(\ds{\mb{p}-\frac{e}{c}\mb{A}}\right)\psi_b =mc\psi_a \\
-\left(\ds{p_0-\frac{e}{c}\phi}\right)\psi_b-\mb{\sigma}\cdot\left(\ds{\mb{p}-\frac{e}{c}\mb{A}}\right)\psi_a =mc\psi_b
\end{cases}
\tag{10}
\end{align*}
以下はランダウ：「量子力学」§ 93 の文章を多少修正したものだが, これらは以前にブログ記事：「Pauli方程式」にしてあるので, 詳しい式の導出などは行わない．上式に於いて,
\begin{equation*}
p_0=\frac{i\hbar}{c}\pdiff{t},\quad \mb{p}=-i\hbar\nabla
\end{equation*}
p_0=\frac{i\hbar}{c}\pdiff{t},\quad \mb{p}=-i\hbar\nabla
\end{equation*}
である [8][ブログ註] ランダウの本文では \(\displaystyle \hat{\mb{p}}=i\hbar\nabla\) となっている．また, 式(10) の \(\pi_0\) に相当する部分が \(p_0-e\phi\) … Continue reading．しかしながら, 非相対論的近似に移行するためには, あらかじめ波動関数にある変換をしておく必要がある．すなわち, 粒子のエネルギーの相対論的表式(及びそれと共に相対論的ハミルトニアン) は (非相対論的な式に比べて) 余分な項, すなわち静止エネルギー \(mc^{2}\) を含んでいるという問題がある．このために波動関数の時間依存性の中に余分な因子 \(\exp(-imc^{2}t/\hbar)\) が現れる．この因子を消去するために \(\psi\) の代わりに次のような \(\psi’\) を導入しよう：
\begin{equation*}
\psi=\psi’\,e^{-imc^{2}t/\hbar}
\tag{11}
\end{equation*}
\psi=\psi’\,e^{-imc^{2}t/\hbar}
\tag{11}
\end{equation*}
式 (11) を式 (10) に代入すると, 4 成分の \(\psi’\) を構成する 2 成分量 \(\psi’_a\) と \(\psi’_b\) に対する次のような方程式を得る：
\begin{align*}
\left(i\hbar\pdiff{t}-e\phi\right)\psi’_a &= c\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi’_b,\tag{12}\\
\left(i\hbar\pdiff{t}-e\phi+2mc^{2}\right)\psi’_b &= c\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi’_a\tag{13}
\end{align*}
(以下 \(\psi’_a\) と \(\psi’_b\) のダッシュを取ることにする)．方程式 (13) の左辺の括弧内に於いて, 一次近似では最大項 \(2mc^{2}\) だけを残そう．するとこの方程式から, 直ちに \(\psi_b\) を \(\psi_a\) を使って表すことが出来る：
\begin{equation*}
2mc^{2}\psi_b = c\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi_a\quad\rightarrow\quad
\psi_b = \frac{1}{2mc}\mb{\sigma}\cdot \left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi_a
\tag{14}
\end{equation*}
2mc^{2}\psi_b = c\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi_a\quad\rightarrow\quad
\psi_b = \frac{1}{2mc}\mb{\sigma}\cdot \left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi_a
\tag{14}
\end{equation*}
等式の右辺の因子 \(1/c\) は, このとき \(\psi_a\) に比べて \(\psi_b\) が小さいことを表している．今度は, 式 (14) を式 (12) に代入し \(\psi_a\) だけを含む方程式を得る：
\begin{equation*}
\left(i\hbar\pdiff{t}-e\phi\right)\psi_a
=\frac{1}{2m}\left\{\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right\}^{2}\psi_a
\tag{15}
\end{equation*}
\left(i\hbar\pdiff{t}-e\phi\right)\psi_a
=\frac{1}{2m}\left\{\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right\}^{2}\psi_a
\tag{15}
\end{equation*}
この方程式の右辺を展開しよう．このとき, パウリ行列の次のような性質が使われる．これはその定義
\begin{equation*}
\sigma_x=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix},\quad
\sigma_y=\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix},\quad
\sigma_z=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
\end{equation*}
\sigma_x=\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix},\quad
\sigma_y=\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix},\quad
\sigma_z=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}
\end{equation*}
から直接に出てくる：
\begin{equation*}
\sigma_{x}^{2}=\sigma_{y}^{2}=\sigma_{z}^{2}=1,\quad
\sigma_{y}\sigma_{z}=-\sigma_{z}\sigma_{y}=i\sigma_{x},\quad
\sigma_{z}\sigma_{x}=-\sigma_{x}\sigma_{z}=i\sigma_{y},\quad
\sigma_{x}\sigma_{y}=-\sigma_{y}\sigma_{x}=i\sigma_{z},
\tag{16}
\end{equation*}
\sigma_{x}^{2}=\sigma_{y}^{2}=\sigma_{z}^{2}=1,\quad
\sigma_{y}\sigma_{z}=-\sigma_{z}\sigma_{y}=i\sigma_{x},\quad
\sigma_{z}\sigma_{x}=-\sigma_{x}\sigma_{z}=i\sigma_{y},\quad
\sigma_{x}\sigma_{y}=-\sigma_{y}\sigma_{x}=i\sigma_{z},
\tag{16}
\end{equation*}
いま \(\displaystyle \hat{\mb{f}}=\left(\mb{p}-\frac{e}{c}\mb{A}\right)\) と置き, 次のように書く：
\begin{align*}
\bigl(\mb{\sigma}\hat{\mb{f}}\bigr)^{2}&=\bigl(\sigma_x\hat{f}_x+\sigma_y\hat{f}_y+\sigma_z\hat{f}_z\bigr)\bigl(\sigma_x\hat{f}_x+\sigma_y\hat{f}_y+\sigma_z\hat{f}_z\bigr)\\
&=\hat{f}_{x}^{\,2}+\hat{f}_{y}^{\,2}+\hat{f}_{z}^{\,2}+i\sigma_{z}\bigl(\hat{f}_{x}\hat{f}_{y}-\hat{f}_{y}\hat{f}_{x}\bigr)
+i\sigma_{x}\bigl(\hat{f}_{y}\hat{f}_{z}-\hat{f}_{z}\hat{f}_{y}\bigr)
+i\sigma_{y}\bigl(\hat{f}_{z}\hat{f}_{x}-\hat{f}_{x}\hat{f}_{z}\bigr)
\end{align*}
もしも \(\hat{f}_{x},\hat{f}_{y},\hat{f}_{z}\) が可換ならば, 簡単に \(\hat{\mb{f}}^{2}\) を得る．しかし今の場合,
\begin{align*}
\hat{f}_{x}\hat{f}_{y}-\hat{f}_{y}\hat{f}_{x}
&=\left(-i\hbar\pdiff{x}-\frac{e}{c}A_x\right)\left(-i\hbar\pdiff{y}-\frac{e}{c}A_y\right)
-\left(-i\hbar\pdiff{y}-\frac{e}{c}A_y\right)\left(-i\hbar\pdiff{x}-\frac{e}{c}A_x\right)\\
&=\frac{ie\hbar}{c}\left(\ppdiff{A_y}{x}-\ppdiff{A_x}{y}\right)=\frac{ie\hbar}{c}H_{z}
\end{align*}
などである．ここで \(\mb{H}=\mathrm{rot}\,\mb{A}\) は磁場である．こうして
\begin{equation*}
\left\{\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right\}^{2}
=\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{c}\mb{\sigma}\cdot\mb{H}
\tag{17}
\end{equation*}
\left\{\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right\}^{2}
=\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{c}\mb{\sigma}\cdot\mb{H}
\tag{17}
\end{equation*}
となる (この式は, 下記の式(25)のように, 公式 (24) を用いて容易に導出できる)．この結果, 2 成分波動関数 \(\psi_a\) に対する次のような方程式に到達する：
\begin{equation*}
i\hbar\ppdiff{\psi_a}{t}=\left[\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}+e\phi\right]\psi_a = H\,\psi_a
\tag{18}
\end{equation*}
i\hbar\ppdiff{\psi_a}{t}=\left[\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{H}+e\phi\right]\psi_a = H\,\psi_a
\tag{18}
\end{equation*}
この式が所謂「パウリ方程式」である．ここに現れたハミルトニアン\(H\)から,電子は磁気モーメントを持ち,次の演算子
\begin{equation*}
\hat{\mb{\mu}}=\frac{e\hbar}{2mc}\mb{\sigma}=\frac{e\hbar}{mc}\hat{\mb{s}}
\tag{19}
\end{equation*}
\hat{\mb{\mu}}=\frac{e\hbar}{2mc}\mb{\sigma}=\frac{e\hbar}{mc}\hat{\mb{s}}
\tag{19}
\end{equation*}
がそれに相当する．ここで\(\hat{\mb{s}}=\mb{\sigma}/2\)は,電子の「スピン演算子」である．このモーメントの大きさ\(\mu\)は
\(\displaystyle \mb{\mu}=\mu\frac{\mb{s}}{s}\)により決定され,
\begin{equation*}
\mu=\frac{e\hbar}{2mc}
\tag{20}
\end{equation*}
\mu=\frac{e\hbar}{2mc}
\tag{20}
\end{equation*}
に等しい．電子の固有磁気モーメントの磁気回転比 \((e/mc)\) は, その軌道運動と結び付いた磁気モーメントに対するものの ２ 倍であることが分かる．この結果は 1928 年にディラックが出した．方程式 (18) を満足する2成分波動関数は, ディラックが彼の方程式を見出す前にすでにパウリにより導かれた(1927)．
次に J.J.Sakurai：「Advanced Quantum Mechanics」§ 3.2 や, ランダウ：「相対論的量子力学」§ 33 を参照して, パウリ運動方程式中の運動エネルギー \(E_{\mathrm{Pauli}}\) とディラック方程式中の静止エネルギーと運動エネルギーの和 \(E_{\mathrm{Dirac}}\) との関係式
\begin{equation*}
E_{\mathrm{Dirac}}=\sqrt{2mc^{2}E_{\mathrm{Pauli}}+m^{2}c^{4}}
\tag{21}
\end{equation*}
E_{\mathrm{Dirac}}=\sqrt{2mc^{2}E_{\mathrm{Pauli}}+m^{2}c^{4}}
\tag{21}
\end{equation*}
を求めてみよう．電子の通常の波動力学的取り扱いでは, ベクトルポテンシャルが無い場合の運動エネルギーの演算子は次のように選ばれる：
\begin{equation*}
H^{\mathrm{KE}}=\frac{\mb{p}^{2}}{2m}
\tag{22}
\end{equation*}
H^{\mathrm{KE}}=\frac{\mb{p}^{2}}{2m}
\tag{22}
\end{equation*}
しかしスピン \(1/2\) 粒子の場合, 我々は次式を用いて始めても良い：
\begin{equation*}
H^{\mathrm{KE}}=\frac{(\mb{\sigma}\cdot\mb{p})(\mb{\sigma}\cdot\mb{p})}{2m}
\tag{23}
\end{equation*}
H^{\mathrm{KE}}=\frac{(\mb{\sigma}\cdot\mb{p})(\mb{\sigma}\cdot\mb{p})}{2m}
\tag{23}
\end{equation*}
この代替的な形式は, ベクトルポテンシャルが存在しない場合, 事実上, 式 (21) と区別を付けることは出来ない．次の非常に重要な恒等式は, たとえ \(\mb{A},\mb{B}\) が演算子であっても成立する：
\begin{equation*}
\color{blue}{(\mb{\sigma}\cdot\mb{A})(\mb{\sigma}\cdot\mb{B})=\mb{A}\cdot\mb{B}+i\mb{\sigma}\cdot(\mb{A}\times\mb{B})}
\tag{24}
\end{equation*}
\color{blue}{(\mb{\sigma}\cdot\mb{A})(\mb{\sigma}\cdot\mb{B})=\mb{A}\cdot\mb{B}+i\mb{\sigma}\cdot(\mb{A}\times\mb{B})}
\tag{24}
\end{equation*}
これを用いると, 式 (23) は式 (22) に一致するからである：
\begin{equation*}
\frac{1}{2m}(\mb{\sigma}\cdot\mb{p})(\mb{\sigma}\cdot\mb{p})
=\frac{1}{2m}\left\{\mb{p}\cdot\mb{p}+i\mb{\sigma}\cdot(\mb{p}\times\mb{p})\right\}
=\frac{1}{2m}\mb{p}^{2}
\end{equation*}
\frac{1}{2m}(\mb{\sigma}\cdot\mb{p})(\mb{\sigma}\cdot\mb{p})
=\frac{1}{2m}\left\{\mb{p}\cdot\mb{p}+i\mb{\sigma}\cdot(\mb{p}\times\mb{p})\right\}
=\frac{1}{2m}\mb{p}^{2}
\end{equation*}
しかしながら \(\mb{p}\to \mb{p}-(e/c)\mb{A}\) と置き換えた場合には違いがある．その場合, 表現式 (23) は次となる：
\begin{align*}
\frac{1}{2m}\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)
&=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}+\frac{i}{2m}\mb{\sigma}\cdot
\left[\left(\mb{p}-\frac{e}{c}\mb{A}\right)\times\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right]\\
&=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}
\tag{25}
\end{align*}
なぜなら,
\begin{align*}
\left(\mb{p}-\frac{e}{c}\mb{A}\right)\times \left(\mb{p}-\frac{e}{c}\mb{A}\right)
&=\mb{p}\times\mb{p}-\frac{e}{c}\mb{p}\times\mb{A}-\frac{e}{c}\mb{A}+\left(\frac{e}{c}\right)
\mb{A}\times\mb{A}\\
&=-\frac{e}{c}\bigl(\mb{p}\times\mb{A}+\mb{A}\times\mb{p}\bigr)
=-\frac{e}{c}\bigl(\mb{p}\times\mb{A}\bigr)
\end{align*}
このとき, 演算子 \(\mb{p}\) の右には波動関数 \(\phi\) が存在しそれにも作用することに注意する：
\begin{align*}
\bigl(\mb{p}\times\mb{A}+\mb{A}\times\mb{p}\bigr)\phi
&=\mb{p}\times\mb{A}\phi + \mb{A}\times\mb{p}\phi
=(\mb{p}\times\mb{A})\phi -\cancel{\mb{A}\times(\mb{p}\phi)}+\cancel{\mb{A}\times\mb{p}\phi}\\
&=(\mb{p}\times\mb{A})\phi
\end{align*}
従って, 式 (25) の右辺第 2 項の導出となる：
\begin{align*}
\frac{i}{2m}\mb{\sigma}\cdot \left[\left(\mb{p}-\frac{e}{c}\mb{A}\right)\times\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right]
&=-\frac{ie}{2mc}\mb{\sigma}\cdot\bigl(\mb{p}\times\mb{A}\bigr)
=-\frac{ie}{2mc}\mb{\sigma}\cdot\left(-i\hbar\nabla\times\mb{A}\right)\\
&=-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\bigl(\nabla\times\mb{A}\bigr)
=-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}
\end{align*}
よって, 本文の式 (9-4) にも示されてある様に, パウリ方程式のハミルトニアンは
\begin{equation*}
H=\frac{1}{2m}\left[\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right]^{2}+e\phi
=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}
+e\phi
\tag{26}
\end{equation*}
H=\frac{1}{2m}\left[\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\right]^{2}+e\phi
=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}
+e\phi
\tag{26}
\end{equation*}
であり, そしてパウリ方程式は次となる：
\begin{equation*}
i\hbar \ppdiff{\psi}{t} = H \psi = \left[\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}-e\phi \right]\psi
\tag{27}
\end{equation*}
i\hbar \ppdiff{\psi}{t} = H \psi = \left[\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}-e\phi \right]\psi
\tag{27}
\end{equation*}
このとき, ハミルトニアン中に第 2 項が出現する点で, 非相対論的シュレディンガー方程式と異なっている．この項は外場内に於ける磁気的 2 重極のポテンシャルエネルギーの形をしている：
\begin{equation*}
V=-\mb{\mu}\cdot\mb{B}=-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}
\end{equation*}
V=-\mb{\mu}\cdot\mb{B}=-\frac{e\hbar}{2mc}\mb{\sigma}\cdot\mb{B}
\end{equation*}
このように \(1/c\) に関する1次近似では, 電子は電荷と共に磁気モーメント \(\mb{\mu}\) を持つ粒子のように振る舞うことは前述した通りである．以上から, パウリ方程式中の運動エネルギー \(E_{\mathrm{Pauli}}\) は次となる：
\begin{equation*}
E_{\mathrm{Pauli}}=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\quad \rightarrow\quad
\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}= 2m E_{\mathrm{Pauli}}
\tag{28}
\end{equation*}
E_{\mathrm{Pauli}}=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\quad \rightarrow\quad
\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}= 2m E_{\mathrm{Pauli}}
\tag{28}
\end{equation*}
他方, 相対論的力学 (Diracの場合) では, ハミルトニアンは次で与えられる (\(\phi=0\)の場合)：
\begin{equation*}
\frac{(H-e\phi)^{2}}{c^{2}}=m^{2}c^{2}+\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\quad \rightarrow\quad
\frac{H^{2}}{c^{2}}=m^{2}c^{2}+\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\end{equation*}
\frac{(H-e\phi)^{2}}{c^{2}}=m^{2}c^{2}+\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\quad \rightarrow\quad
\frac{H^{2}}{c^{2}}=m^{2}c^{2}+\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\end{equation*}
従って,
\begin{equation*}
\frac{E^{2}_{\mathrm{Dirac}}}{c^{2}}=m^{2}c^{2}+\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\quad \rightarrow\quad
E^{2}_{\mathrm{Dirac}}=m^{2}c^{4}+c^{2}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\end{equation*}
\frac{E^{2}_{\mathrm{Dirac}}}{c^{2}}=m^{2}c^{2}+\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\quad \rightarrow\quad
E^{2}_{\mathrm{Dirac}}=m^{2}c^{4}+c^{2}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
\end{equation*}
これに式 (28) の結果を用いると, 題意の式 (21) が得られる：
\begin{equation*}
E^{2}_{\mathrm{Dirac}}=m^{2}c^{4}+c^{2}\times 2m E_{\mathrm{Pauli}}
\quad \rightarrow\quad
E_{\mathrm{Dirac}}=\sqrt{m^{2}c^{4}+2mc^{2}E_{\mathrm{Pauli}}}
\end{equation*}
E^{2}_{\mathrm{Dirac}}=m^{2}c^{4}+c^{2}\times 2m E_{\mathrm{Pauli}}
\quad \rightarrow\quad
E_{\mathrm{Dirac}}=\sqrt{m^{2}c^{4}+2mc^{2}E_{\mathrm{Pauli}}}
\end{equation*}
しかしながらパウリ方程式は, ディラック方程式の非相対論的近似を (\(1/c\)) まで行って得た式である．近似を \(1/c^{2}\) まで行った場合のハミルトニアンは, 後の第12講に於いて式 (12-6) で求められている：
\begin{align*}
H = e\phi + \frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e}{2mc}\mb{\sigma}\cdot\mb{B}
-\frac{1}{8m^{3}c^{2}}\bigl(\mb{p}\cdot\mb{p}\bigr)^{2}+\frac{e\hbar^{2}}{8m^{2}c^{2}}\nabla\cdot\mb{E}
+\frac{e\hbar}{4m^{2}c^{2}}\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\times\mb{E}
\end{align*}
ただし \(\mb{E}=-\nabla\phi\) は電場の強さである．従って, ポテンシャルが \(\phi=0\) である場合の式は次となる：
\begin{equation*}
H=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e}{2mc}\mb{\sigma}\cdot\mb{B}
-\frac{\mb{p}^{4}}{8m^{3}c^{2}}
\tag{29}
\end{equation*}
H=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}-\frac{e}{2mc}\mb{\sigma}\cdot\mb{B}
-\frac{\mb{p}^{4}}{8m^{3}c^{2}}
\tag{29}
\end{equation*}
この式 (29) 中の第 3 項は, 粒子の運動エネルギーの古典式に対する相対論的補正に対応している．すなわち,
\begin{equation*}
\sqrt{c^{2}\mb{p}^{2}+m^{2}c^{4}} -mc^{2}
\approx \frac{\mb{p}^{2}}{2m}-\frac{\mb{p}^{4}}{8m^{3}c^{2}}+\dotsb
\tag{30}
\end{equation*}
\sqrt{c^{2}\mb{p}^{2}+m^{2}c^{4}} -mc^{2}
\approx \frac{\mb{p}^{2}}{2m}-\frac{\mb{p}^{4}}{8m^{3}c^{2}}+\dotsb
\tag{30}
\end{equation*}
よって, 近似を \(1/c^{2}\) まで行った場合の運動エネルギーを \(E^{(2)}\) と書くならば, 式 (28) に相当する式は,
\begin{equation*}
E^{(2)}=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
-\frac{\mb{p}^{4}}{8m^{3}c^{2}}
\tag{31}
\end{equation*}
E^{(2)}=\frac{1}{2m}\left(\mb{p}-\frac{e}{c}\mb{A}\right)^{2}
-\frac{\mb{p}^{4}}{8m^{3}c^{2}}
\tag{31}
\end{equation*}
となり, また題意の式 (21) に相当するのは, より複雑な次のような式となるであろう：
\begin{equation*}
E_{\mathrm{Dirac}}=\sqrt{m^{2}c^{4}+2mc^{2}E^{(2)}+\frac{\mb{p}^{4}}{4m^{2}}}
\tag{32}
\end{equation*}
E_{\mathrm{Dirac}}=\sqrt{m^{2}c^{4}+2mc^{2}E^{(2)}+\frac{\mb{p}^{4}}{4m^{2}}}
\tag{32}
\end{equation*}
Dirac方程式の非相対論的近似(NONRELATIVISTIC APPROXIMATION TO THE DIRAC EQUATION)
ポテンシャルは全て静的であることを仮定し, そして状態は静的な状態を考える．このことは作業を簡単化するが, 必ずじも必要ではない．
この場合,
\begin{equation*}
\psi=e^{-iEt/\hbar}\psi(x),\quad H\psi = E\psi\quad (\mathrm{Dirac}\ \mathrm{Hamiltonian})
\end{equation*}
\psi=e^{-iEt/\hbar}\psi(x),\quad H\psi = E\psi\quad (\mathrm{Dirac}\ \mathrm{Hamiltonian})
\end{equation*}
そして次と置く：
\begin{equation*}
E = mc^{2} + W
\end{equation*}
E = mc^{2} + W
\end{equation*}
すなわち,
\begin{equation*}
H\psi = (mc^{2}+W)\psi = c\mb{\alpha}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi +\beta mc^{2}\psi + e\phi\psi
\end{equation*}
H\psi = (mc^{2}+W)\psi = c\mb{\alpha}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi +\beta mc^{2}\psi + e\phi\psi
\end{equation*}
\(\psi\) を式 (9-5) のように書き, また \(\alpha,\beta\) を講義 \(10\) で示したように書くと, 前の式は 2 つの式 (9-6) のように書けることを思い出してほしい：
\begin{align*}
(mc^{2}+W)\psi_a &= c\mb{\sigma}\cdot\mb{\pi}\,\psi_b + mc^{2}\psi_a + V\psi_a,\tag{11-4}\\
(mc^{2}+W)\psi_b &= c\mb{\sigma}\cdot\mb{\pi}\,\psi_a – mc^{2}\psi_b + V\psi_b,\tag{11-5}
\end{align*}
ただし, 前述と同様に \(\displaystyle \mb{\pi}=\left(\mb{p}-\frac{e}{c}\mb{A}\right)\) そして \(V=e\phi\) である．式 (11-5) を簡単化して \(\psi_b\) について解くならば,
\begin{equation*}
\psi_b =\frac{1}{2mc^{2}+W-V}c\mb{\sigma}\cdot\mb{\pi}\,\psi_a
\tag{11-6}
\end{equation*}
\psi_b =\frac{1}{2mc^{2}+W-V}c\mb{\sigma}\cdot\mb{\pi}\,\psi_a
\tag{11-6}
\end{equation*}
このとき, もし \(W\) と \(V\) が \(\ll 2mc^{2}\) とすると \(\displaystyle \psi_b\sim \frac{v}{c}\psi_a\) であることに注意する：
\begin{align*}
\psi_b &\approx \frac{c}{2mc^{2}}\mb{\sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)\psi_a
=\frac{m\mb{v}\cdot\mb{\sigma}}{2mc}\psi_a -\frac{e}{2mc^{2}}\mb{A}\cdot\mb{\sigma}\psi_a
\approx \frac{1}{2c}\mb{v}\cdot\mb{\sigma}\,\psi_a \sim \frac{v}{c}\psi_a,\\
\quad &\mathrm{where}\quad \mb{v}\cdot\mb{\sigma}\,\psi_a =
\begin{pmatrix} v_z & v_x-iv_y \\ v_x+iv_y & -v_z \end{pmatrix}\psi_a \sim v\,\psi_a
\end{align*}
この理由から, ときどき \(\psi_a\) と \(\psi_b\) は, 各々 \(\psi\) の「大きい成分」及び「小さい成分」と呼ばれることがある．式 (11-6) の \(\psi_b\) を式 (11-4) へ代入すると次式を得る：
\begin{equation*}
W\psi_a =\mb{\sigma}\cdot\mb{\pi}\,\frac{c^{2}}{2mc^{2}+W-V}\,\mb{\sigma}\cdot\mb{\pi}\,\psi_a + V\psi_a
\tag{11-7}
\end{equation*}
W\psi_a =\mb{\sigma}\cdot\mb{\pi}\,\frac{c^{2}}{2mc^{2}+W-V}\,\mb{\sigma}\cdot\mb{\pi}\,\psi_a + V\psi_a
\tag{11-7}
\end{equation*}
そして \(2mc^{2}\) と比較して \(W\) と \(V\) を無視するならば, 結果は次となる：
\begin{equation*}
W\psi_a =\frac{1}{2m}\bigl(\mb{\sigma}\cdot\mb{\pi}\bigr)^{2}\,\psi_a + V\psi_a
\end{equation*}
W\psi_a =\frac{1}{2m}\bigl(\mb{\sigma}\cdot\mb{\pi}\bigr)^{2}\,\psi_a + V\psi_a
\end{equation*}
これは, 式 (9-4) のパウリ方程式である!．
さて次は, パウリ方程式を利用することでどんな誤差が予想されるかを明らかにするために, 2 次までの近似, すなわち \(v^{2}/c^{2}\) のオーダーまでの近似をやってみよう．
References
| ↑1 | Schiff (“Quantum Mechanics,” McGraw-Hill, New York, 1949) のハミルトニアンは, ここでのハミルトニアンと違ってマイナス符号が \(e\phi\) を除いて付いている．また Schiff で用いられる波動関数の成分 \(\psi_1\), \(\psi_2\), \(\psi_3\), \(\psi_4\) は, 各々がここでの \(-\psi_{b_1}\), \(-\psi_{b_2}\), \(-\psi_{a_1}\), \(\psi_{a_2}\) に相当している．これらの違いの全ては, ここでの表現と Schiff で用いられている表現間の等価変換が \(S^{2}=i\beta\alpha_x\alpha_y\alpha_z\) であることに起因している．\(S^{2}=-1\) 従って \(S^{-1}=-S\) そして次であることの証明は容易である： \begin{equation*} S^{-1}=\begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{pmatrix} =\begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \end{equation*} |
|---|---|
| ↑2 | [ブログ註] \(\alpha_1,\psi,\psi^{*}\)に具体的な行列表現を代入するだけである： \begin{align*} \psi^{*}\alpha_1\psi &=\begin{pmatrix}\psi^{*}_{1}\!\!\! & \psi^{*}_{2}\!\!\! & \psi^{*}_{3}\!\!\! & \psi^{*}_{4} \end{pmatrix} \begin{pmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} \psi_{1} \\ \psi_{2} \\ \psi_{3} \\ \psi_{4} \end{pmatrix} =\begin{pmatrix}\psi^{*}_{1}\!\!\! & \psi^{*}_{2}\!\!\! & \psi^{*}_{3}\!\!\! & \psi^{*}_{4} \end{pmatrix} \begin{pmatrix} \psi_{4} \\ \psi_{3} \\ \psi_{2} \\ \psi_{1} \end{pmatrix}\\ &=\psi^{*}_{1}\psi_{4}+\psi^{*}_{2}\psi_{3}+\psi^{*}_{3}\psi_{2}+\psi^{*}_{4}\psi_{1} \end{align*} |
| ↑3 | [ブログ註] 時間発展演算子を \(\mathscr{U}(t)=\exp(-iHt/\hbar)\) とするならば, シュレディンガー表示の観測量 \(A\) のハイゼンベルグ表示は \(A(t)\equiv\mathscr{U}^{\dagger}(t)A\mathscr{U}(t)\) で定義される．これを時間微分した関係などは, \(\mathscr{U}\) と \(H\) とは可換なので \(\mathscr{U}^{\dagger}H\mathscr{U}=H\) となることなどから, \begin{equation*} \dot{\mathscr{U}}=-\frac{i}{\hbar}H\mathscr{U},\quad \dot{\mathscr{U}^{\dagger}}=\frac{i}{\hbar}\mathscr{U}^{\dagger}H,\quad \mathscr{U}^{\dagger}HA\mathscr{U}=\mathscr{U}^{\dagger}H\mathscr{U}\mathscr{U}^{\dagger}A\mathscr{U} =HA(t),\quad \mathscr{U}^{\dagger}\ppdiff{A}{t}\mathscr{U}=\ppdiff{A(t)}{t} \end{equation*} これらを用いると, \begin{align*} \frac{dA}{dt}&=\ppdiff{\mathscr{U}^{\dagger}}{t}A\mathscr{U} +\mathscr{U}^{\dagger}\ppdiff{A}{t}\mathscr{U} +\mathscr{U}^{\dagger} A\ppdiff{\mathscr{U}}{t} =\frac{i}{\hbar}\mathscr{U}^{\dagger}HA\mathscr{U}-\frac{i}{\hbar}\mathscr{U}^{\dagger} AH\mathscr{U} +\mathscr{U}^{\dagger}\ppdiff{A}{t}\mathscr{U}\\ &=\frac{i}{\hbar}HA(t)-\frac{i}{\hbar}A(t)H+\ppdiff{A(t)}{t} =\frac{i}{\hbar}\bigl[H,A(t)\bigr] + \ppdiff{A(t)}{t} \end{align*} |
| ↑4 | この議論は完全に受容できると言うわけではない．なぜなら \(\dot{\mb{x}}\) は \(\mb{p}\) と交換する．即ち, 同時に ２つの量を測定することが可能でなければならないからである． |
| ↑5 | [ブログ註] 荷電粒子が円運動を行えば, 磁気双極子モーメントと角運動量を生じる．素粒子系の持つ磁気双極子モーメントと角運動量の比を「磁気回転比」と言う．電子の磁気回転比は正確に \(2\) ではない．その値は, \begin{equation*} g=2\left[1 + \left(\frac{e^{2}}{4\pi\hbar c}\right)\frac{1}{2\pi}+\dotsb \right] \end{equation*} のように与えられる．この余分な磁気能率の起源を,「電子が仮想的な光子を放出したり吸収したりする効果として説明できることを J.Schwinger が 1947 年に示した． |
| ↑6 | [ブログ註] 運動量 \(\mb{p}\) の向きの単位ベクトル \(\hat{\mb{p}}=\mb{p}/|\mb{p}|\) と一般化スピン \(\mb{\Sigma}\) との内積を「ヘリシティ演算子」(helicity operator) と呼ぶ： \[\mb{\Sigma}\cdot\hat{\mb{p}}=\mb{\Sigma}\cdot\left(\frac{\mb{p}}{|\mb{p}|}\right)=\frac{\mb{\Sigma}\cdot\mb{p}}{|\mb{p}|}\] ヘリシティーが \(+1\) の固有状態 (スピンと運動方向が一致している) を「右巻き状態」と言い, ヘリシティーが \(-1\) の固有状態 (スピンと運動方向が反対向き) を「左巻き状態」と呼ぶ． |
| ↑7 | [ブログ註] (ランダウ §48 より) 一様な磁場 \(\mb{H}\) の中での電荷 \(e\) の運動を考える．磁場の方向を \(z\) 軸にとる．運動方程式 \(\displaystyle \dot{\mb{p}}=\frac{e}{c}\mb{v}\times\mb{H}\) に於いて, 運動量の式 \(\displaystyle \mb{p}=\frac{m\mb{v}}{\sqrt{1-\beta^{2}}}\) から得られる式として次がある： \begin{equation*} \mb{p}=\frac{m\mb{v}}{\sqrt{1-\beta^{2}}}=\frac{mc^{2}}{c^{2}\sqrt{1-\beta^{2}}}\mb{v} =\frac{\mathscr{E}}{c^{2}}\mb{v} \end{equation*} ただし \(\mathscr{E}\) は粒子のエネルギーであり, 磁場中では一定である．すると, \begin{equation*} \dot{\mb{p}}=\frac{\mathscr{E}}{c^{2}}\dot{\mb{v}}=\frac{e}{c}\mb{v}\times\mb{H},\quad\rightarrow\quad \dot{\mb{v}}=\frac{ec}{\mathscr{E}}\mb{v}\times{\mb{H}} \end{equation*} 従って, これを成分で書くと, \begin{equation*} \frac{dv_x}{dt}=\omega v_y,\quad \frac{dv_y}{dt}=-\omega v_x,\quad \frac{dv_z}{dt}=0,\quad\mathrm{where}\quad \omega=\frac{ecH}{\mathscr{E}} \end{equation*} この式は, 電荷は一様な磁場中で螺旋を描いて運動することを表している．電荷が場の方向 (z方向) の速度成分を持たない特別な場合には, 電荷は場に垂直な面の中で, 半径 \(\displaystyle r=\frac{\sqrt{v_x^{2}+v_y^{2}}}{\omega}\) の円周上を動くことになる．\(\omega\) という量は, 場に垂直な面の中での粒子の回転運動の角周波数である．不変な電磁場中の電荷のエネルギーは保存されるが, その大きさ \(\mathscr{E}\) は, \begin{equation*} \mathscr{E}=\frac{mc^{2}}{\sqrt{1-\beta^{2}}}+e\phi \quad\rightarrow\quad \mathscr{E}=\frac{mc^{2}}{\sqrt{1-\beta^{2}}} \quad \mathrm{when}\ \phi=0,\quad \beta=\frac{v}{c} \end{equation*} 従って, その回転運動の角周波数は次となる： \begin{equation*} \omega=\frac{ecH}{\mathscr{E}}=ecH\times\frac{\sqrt{1-\beta^{2}}}{mc^{2}}=\frac{eH}{mc}\sqrt{1-\beta^{2}} \end{equation*} |
| ↑8 | [ブログ註] ランダウの本文では \(\displaystyle \hat{\mb{p}}=i\hbar\nabla\) となっている．また, 式(10) の \(\pi_0\) に相当する部分が \(p_0-e\phi\) となっている．しかし, 前節の式 (92.2) を普通の単位を用いて書くならば, \begin{equation*} \hat{p}_{\mu}\longrightarrow \hat{p}_{\mu}-\frac{e}{c}A_{\mu},\quad A^{\mu}=(\phi,\mb{A})\quad \mathrm{or}\quad \pi_0=p_0-\frac{e}{c}\phi,\quad \mb{\pi}=\mb{p}-\frac{e}{c}\mb{A},\quad p_0=i\hbar\frac{\partial}{\partial(ct)},\quad \mb{p}=-i\hbar\nabla \end{equation*} となる．従って, これらは明らかにミスプリントであろう． |
