Sixteenth Lecture
核\(K_{+}(2,1)\)の使用法(USE OF THE KERNEL)
\(
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\half{\frac{1}{2}}
\def\Slash#1{#1\!\llap{/}\,}
\def\SlashA{A\llap{/}\,}
\def\BraKet#1#2#3{\left\langle #1 | #2 | #3 \right\rangle}
\def\BK#1#2{\left\langle #1 | #2 \right\rangle}
\)
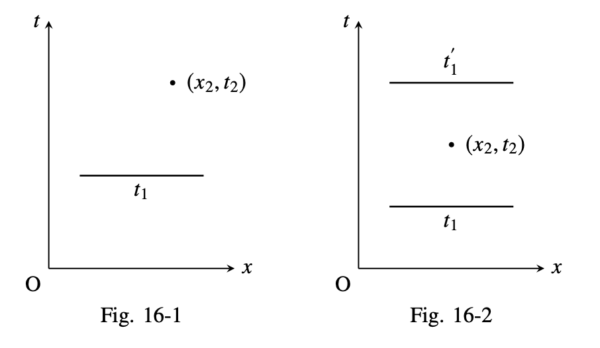
非相対論的理論においては, 時刻 \(t_2\) に於ける点 \(\mb{x_2}\) での波動関数が, 非相対論的核 \(K_0(2,1)\) を用いることで, 以前の時刻 \(t_1\) に於ける波動関数の知識から計算出来た(図16-1参照):
\psi(\mb{x}_2, t_2) = \int K_0(\mb{x}_2,t_2 ,\mb{x}_1, t_{1}) \psi(\mb{x}_1, t_1)\, d^{3}\mb{x}_1
\end{equation*}
これの相対論的な一般化は, 以下のようになると期待するかも知れない:
\psi(\mb{x}_2, t_2) = \int K_{+}(\mb{x}_2,t_2 ,\mb{x}_1, t_{1})\gamma^{0}
\psi(\mb{x}_1, t_1)\, d^{3}\mb{x}_1
\end{equation*}
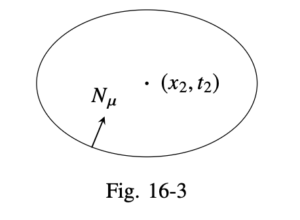
しかしながら, 相対論的なケースに於いてこれは正しくないことが分かる.なぜなら \(t_2 < t_1\) の場合は核がゼロでないからである.点 \(x_2, t_2\) を囲む境界面(図16-2参照) に於いて波動関数が定義されている場合, 点 \(\mb{x}_2, t_2\) における波動関数は次のように与えられる:
\begin{align*}
\psi(\mb{x}_2, t_2) &= \int K_{+}(\mb{x}_2,t_2 ,\mb{x}_1, t_{1})\gamma^{0}
\psi(\mb{x}_1, t_1)\, d^{3}\mb{x}_1\notag\\
&\qquad\qquad – \int K_{+}(\mb{x}_2,t_2 ,\mb{x}_1, t’_{1})\gamma^{0}\psi(\mb{x}_1, t’_1)\, d^{3}\mb{x}_1
\qquad ( t_1 < t_2 < t_1′ )
\tag{16-1}
\end{align*}
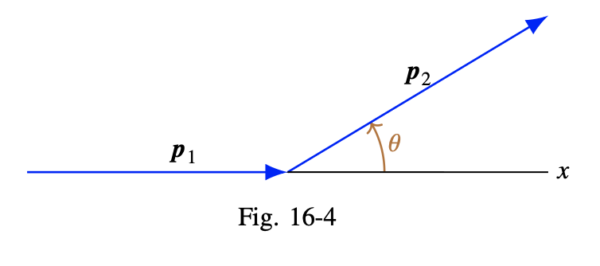
この式の第1項は以前の時刻からの正エネルギー状態の寄与であり, 第2項は後の時刻からの負エネルギー状態の寄与である.この表現は「点 \(\mb{x}_2, t_2\) を囲む4次元表面上の \(\psi(\mb{x}_1, t_1)\) を知る必要がある」という記述に一般化できる(図16-3参照):
\begin{align*}
\psi(\mb{x}_2, t_2) = \int K_+(2,1) \Slash{N}(1) \psi(1)\,d^4x_1
\tag{16-2}
\end{align*}
ここで \(\Slash{N}_\mu\) は点 \(x_2, t_2\) を取り囲む領域表面に垂直な4元ベクトルである.
遷移確率 (TRANSITION PROBABILITY)
ポテンシャル \(\Slash{A}\) の作用下で, 状態 \(f\) から状態 \(g\) へ移行する振幅は, 非相対論的理論と同様の表現で与えられる:
\begin{align*}
a_{21} = \iint \tilde{g}(2) \beta K_+^A(2,1) \beta f(1)\, d^3\mb{x}_1\, d^3\mb{x}_2
\tag{16-3}
\end{align*}
\(K_+^A(2,1)\) を式 (15-12) の \(K_+(2,1)\) で展開し, 自由粒子としての状態 \(f\) から状態 \(g\) への遷移の振幅がゼロである(\(f\) と \(g\) が直交する状態である)と仮定すると, 遷移の第1次近似の振幅(ボルン近似)は次のようになる:
\begin{align*}
a_{21} = -i \int \tilde{g}(2) \beta \int K_+(2,3) e \SlashA(3) K_+(3,1) \beta f(1)\, d\tau_3\, d^3\mb{x}_1\, d^3\mb{x}_2
\end{align*}
ここで, 次のように定義すると便利である:
\begin{align*}
f(3) = \int K_+(3,1) \beta f(1)\, d^3\mb{x}_1,\qquad
\tilde{g}(3) = \int \tilde{g}(2) \beta K_+(2,3)\, d^3\mb{x}_2
\end{align*}
この2式は, 粒子が散乱の直前までは自由粒子の波動関数 \(f\) を持ち, 散乱の直後からは自由粒子の波動関数 \(g\) を持つこと, そして自由粒子としての運動の計算を一切排除することを示している.第1次近似における遷移の振幅は,次のように書くことが出来る:
\begin{align*}
-i \int \tilde{g}(3) e \SlashA(3) f(3)\, d\tau_3
\tag{16-4}
\end{align*}
(\(d\tau_3\) は空間だけでなく時間についての積分も意味する).第2次近似の項は次のように書かれる:
\begin{align*}
-\frac{1}{2} \iint \tilde{g}(4) e \SlashA(4) K_+(4,3) e \SlashA(3) f(3)\, d\tau_3\, d\tau_4
\end{align*}
もし \(f(3)\) が負エネルギー状態であれば, それは未来の陽電子を記述しており過去の電子ではない.そしてこの振幅によって記述される過程は「対生成の過程」となる.
クーロンポテンシャルによる電子の散乱 (SCATTERING OF AN ELECTRON FROM A COULOMB POTENTIAL)
電荷 \(Ze\) を持つ無限に重い原子核による電子の散乱を計算するために, 前述で示した理論を利用する.入射電子は \(x\) 方向に運動量 \(\mb{p}_1\) を持ち, 散乱された電子は \(xy\) 平面内に運動量 \(\mb{p}_2\) を持つと仮定する(図16-4参照).
\begin{align*}
\Slash{p}_1 &=\gamma^{\mu}p_{1\mu}=\gamma^{0}\frac{E_1}{c}-\mb{\gamma}\cdot\mb{p}_1
= \gamma^{0} E_1 – \gamma^{1}p_{1x},\\
\Slash{p}_2 &=\gamma^{\mu}p_{2\mu} = \gamma^{0}\frac{E_2}{c}-\mb{\gamma}\cdot\mb{p}_2
= \gamma^{0}E_2 -\gamma^{1} p_{2x} – \gamma^{2} p_{2y}
\end{align*}
ポテンシャルは静止した電荷 \(Ze\) によるものであり, 次のように表わせる:
\begin{align*}
A^{0}=\phi =\frac{Ze}{r},\quad \mb{A} = 0 \quad\rightarrow\quad \SlashA=\gamma_{0}A^{0}-\mb{\gamma}\cdot\mb{A}
=\gamma^{0}\frac{Ze}{r}
\end{align*}
初期状態および最終状態の自由粒子の波動関数は平面波である:
\begin{align*}
f(1) = u_1 e^{-i p_1 \cdot x}, \quad g(2) = u_2 e^{-i p_2 \cdot x} \quad \text{(4成分の波動関数)}
\end{align*}
したがって, 式 (16-4) により, 状態 \(f\) から状態 \(g\) へ (運動量 \(p_1\) から運動量 \(p_2\) へ) の遷移の第1次近似の振幅は次のようになる:
\begin{align*}
\text{1次遷移振幅:}\quad M = -i \int \tilde{u}_2 e^{i p_2 \cdot x} \frac{Ze^2}{r} \gamma^{0} u_1 e^{-i p_1 \cdot x}\, d^3\mb{x}\, dt
\end{align*}
波動関数の空間依存性と時間依存性を分離すると, これは次のようになる.
\begin{align*}
M = -i (\tilde{u}_2 \gamma^{0} u_1) \left[ \int e^{-i \mb{p}_2 \cdot \mb{x}} \frac{Ze^2}{r} e^{i \mb{p}_1 \cdot \mb{x}}\,
d^3\mb{x} \right] \left[ \int e^{i E_2 t} e^{-i E_1 t}\, dt \right]
\end{align*}
最初の積分は, 非相対論的散乱理論で計算された「ポテンシャルの3次元フーリエ変換 \(V(\mb{q})\)」に他ならない.[1][訳註] 運動量移行を \(\mb{q}=\mb{p}_2-\mb{p}_1\) とする.部分積分を2回行い, \(\nabla^{2}e^{-i\mb{q}\cdot\mb{x}}=-\mb{q}^{2}e^{-i\mb{q}\cdot\mb{x}}\) … Continue reading
従って,
\begin{align*}
M = -i (\tilde{u}_2 \gamma^{0} u_1) V(\mb{q})\times 2\pi \delta(E_2-E_1) ,\qquad
V(\mb{q}) = \frac{4\pi Ze^2}{\mb{q}^2}, \quad \mb{q} = \mb{p}_1 – \mb{p}_2 \tag{16-5}
\end{align*}
「単位時間当たりの遷移確率」は次のように与えられる [2][訳註] 始状態 \(i\) から終状態の組 \([n]\) への単位時間あたりの遷移確率 \(w_{i\to [n]}\) は, … Continue reading:
\begin{align*}
\text{[ 単位時間当たりの遷移確率 ]} = 2\pi \left(\prod N\right)^{-1} |M|^2 \times \text{[ 終状態の密度 ]}
\end{align*}
これは「時間依存する摂動論」の既知の結果であるが, 唯一新しい点は規格化因子 \((\prod N)^{-1}\) である.これは「波動関数が単位体積当たり \(1\) であるように規格化されていない」という事実を考慮している.\(\prod N\) は, 初期状態における各波動関数(あるいは粒子)毎にある因子 \(N_1\) と各最終波動関数毎にある因子 \(N_2\) との積であり, 考えている各粒子に対しては,
\begin{align*}
N_1 = (\tilde{u}_1\gamma^{0} u_1)=2E_1,\quad N_2 = (\tilde{u}_2\gamma^{0} u_2)=2E_2
\tag{16-6}
\end{align*}
である.ここでの規格化では \(N=2E\) である.因子がこのようになる理由は, 波動関数が
\begin{align*}
(\tilde{u} u) = 2m, \quad \text{or}\quad (\tilde{u}\gamma^{0} u) = (u^{\dagger} u) = 2E
\tag{16-7}
\end{align*}
のように規格化されており, そして遷移確率の計算のときと同様に, 波動関数は従来の非相対論的手法である \(\psi^{*}\psi=1\) 即ち \(\tilde{u}\gamma^{0} u=1\) で正規化されるべき(従って, その場合には \(N=1\) である) だからである.このように計算された行列要素 \(M\) は相対論的に不変であるから, 今後の主な関心対象は \(M\) となろう.\(M\) が分かれば, 遷移確率は式 (16-6) から計算できるからである.
状態の密度, 断面積(Density of State, Cross Section)
今考えている電子散乱問題に於いて, 遷移振幅 \(M\) からデルタ関数部分 \(2\pi\delta(E_2-E_1)\) を除いたものを考え, それを「不変振幅」\(\mathcal{M}\) とする:
\begin{align*}
M &= -i (\tilde{u}_2 \gamma^{0} u_1)\frac{4\pi Ze^{2}}{\mb{q}^{2}} \times 2\pi \delta(E_2-E_1)
=i2\pi\delta(E_2-E_1)\times\mathcal{M},\\
\longrightarrow&\quad \mathcal{M}= -(\tilde{u}_2 \gamma^{0} u_1)\frac{4\pi Ze^{2}}{\mb{q}^{2}}
\end{align*}
また「終状態の密度」は, 次のような仕方で得られる(ただし単位体積を考え \(V=1\) とする):
\begin{align*}
\text{[終状態の密度]} = \rho(E_2)dE_2= \frac{d^3 \mb{p}_2}{(2\pi)^3} = \frac{p_2^2 dp_2 d\Omega}{(2\pi)^3},
\quad \hbar = 1
\end{align*}
ところが \(E_2^2 = p_2^2 + m^2\) であり, 従って \( p_2 dp_2 = E_2dE_2\) であるから,
\begin{align*}
\text{[終状態の密度]} =\frac{p_2 dp_2}{dE_2}\frac{p_2 d\Omega}{(2\pi)^{3}}=\frac{E_2p_2 d\Omega}{(2\pi)^{3}}
\end{align*}
従って, 単位時間当たりの遷移確率は次となる(遷移振幅の代わりに不変振幅を用いる) [3][訳註] 時間積分に由来するこのデルタ関数は最終的に \(1\) になるので, … Continue reading:
\begin{align*}
dR &=\text{[単位時間当たりの遷移確率]} =\frac{2\pi}{\left(\prod N\right)}\times |M|^{2}\times \text{[ 終状態の密度 ]}\\
&= \frac{2\pi}{(2E_1)(2E_2)} |(\tilde{u}_2 \gamma^{0} u_1)|^2
\left( \frac{4\pi Ze^2}{\mb{q}^2} \right)^2 \frac{E_2p_2}{(2\pi)^{3}}d\Omega
\tag{16-8}
\end{align*}
入射する平面波が「\(1 \text{cm}^{3}\) 当たり1つの粒子」に規格化されている場合,「断面積」\(d\sigma\) は「単位時間当たりの遷移確率」\(dR\) を用いて次式のように表される:[4]\begin{align*}
p_1=\frac{mv_1}{\sqrt{1-v_1^{2}}}\ \rightarrow\
p_1^{2}=\frac{m^{2}v_1^{2}}{1-v_1^{2}}\ \rightarrow\
p_1^{2}(1-v_1^{2})=m^{2}v_1^{2}\ \rightarrow\
p_1^{2}=(m^{2}+p_1^{2})v_1^{2} … Continue reading
\begin{align*}
dR =v_1\times d\sigma = \frac{p_1}{E_1}\times d\sigma \quad \longrightarrow\quad
d\sigma = \frac{E_1}{p_1}\times dR
\tag{A}
\end{align*}
散乱の相対論的な論述法と非相対論的な論述との本質的な相違は, 行列要素 \(\tilde{u}_2\gamma^{0}u_1\) 中にある.第13講にある表 13-1 から, \(x\)-\(y\) 平面中を運動する粒子で \(s_1=+1\),\(s_2=+1\) の場合,
\begin{align*}
\sqrt{F_1F_2} (\tilde{u}_2\gamma^{0}u_1)=F_2F_1 + c^{2}p_{1+}p_{2+}\quad\longrightarrow\quad
\left| (\tilde{u}_2\gamma^{0}u_1)\right|^{2}= \frac{\left|F_2F_1 + p_{1+} p_{2+}\right|^{2}}{F_1F_2}
\end{align*}
ただし \(c=1\) そして \(F_1=F_2=E+mc^{2}=E+m\) である.[ エネルギー保存 \(E_1=E_2\) は, 式 (16-5) の時間積分の性質 \(2\pi\delta(E_2-E_1)\) に由来する], そして次とする:
\begin{align*}
p_{1+}=p,\qquad p_{2-}=p\,e^{-i\theta}
\end{align*}
[終状態の運動量の大きさが始状態の運動量の大きさに等しいこと \(|\mb{p}_1|=|\mb{p}_2|=p\) は, エネルギー保存 \(\delta(E_2-E_1)\ \rightarrow\ E_1=E_2=E\) から導出される].従って,
\begin{align*}
\left| (\tilde{u}_2\gamma^{0}u_1)\right|^{2} &=\frac{|(E+m)^{2}+p^{2}e^{-i\theta}|^{2}}{(E+m)^{2}}
=\frac{4E^{2}(E+m)^{2}[1-(p^{2}/E^{2})\sin^{2}(\theta/2)]}{(E+m)^{2}}\\
&=(2E)^{2}\left[ 1-v^{2}\sin^{2} \frac{\theta}{2} \right]
\tag{B}
\end{align*}
\(s_1=+1,\,s_2=-1\) または \(s_1=-1,\,s_2=+1\) のとき, \(\gamma^{0}\) の行列要素はゼロである.\(s_1=-1,\,s_2=-1\) のとき, 行列要素の絶対値は \(s_1=+1,\,s_2=+1\) の場合と同じである.従って(Born近似に於いては), 散乱するときスピンは変化せず, そして断面積はスピンに依存しない.
以上の式 (A) に式 (16-8) および式 (B) を代入すると(ただし \(E_1=E_2=E,p_1=p_2=p\) とする),
\begin{align*}
d\sigma &= \frac{E}{p}\times\frac{2\pi}{(2E)(2E)}\times (2E)^{2}\left[ 1-v^{2}\sin^{2} \frac{\theta}{2} \right]
\left( \frac{4\pi Ze^2}{\mb{q}^2} \right)^2 \frac{E p}{(2\pi)^3}d\Omega\\
&=\frac{4Z^{2}e^{4}E^{2}}{q^{4}} d\Omega \left[ 1-v^{2}\sin^{2} \frac{\theta}{2}\right]
\qquad q=2p\,\sin \frac{\theta}{2}
\tag{C}
\end{align*}
この結果を得るのに用いた「ボルン近似」が妥当であるための基準は \(Ze^{2}/\hbar v \ll 1\) である.相対論的極限では \(v\approx c\) である.その場合 \(Z \ll 137\) となる [5][訳註] 結果式 (C) をさらに変形すると,
\begin{align*}
\sigma &=\frac{4Z^{2}e^{4}E^{2}}{\ds{\left(2p\sin\frac{\theta}{2}\right)^{4}}} d\Omega
\left[ 1-v^{2}\sin^{2} … Continue reading.
非相対論の場合と全く同様に, クーロンポテンシャルの場合の散乱は正確に(ポテンシャルの全てのオーダーで正確に) 計算できる.ディラック方程式のこの正確な解は「超幾何関数」(hypergeometric functions)を含んでいる.これは Mott によって初めて導出され,「Mott 散乱」と呼ばれる.中程度のエネルギー(\(200\) keV)では, スピン変化が多少は有り得る.従って, この方法により偏極電子を生成することが可能である.
【 問題 】
(1) クライン-ゴルドン方程式(スピンのない粒子)に対するラザフォード散乱公式を計算せよ.
( 結果:上記の公式で \(1 – v^2 \sin^2(\theta/2)\) を \(1\) で置き換えたものになる.)
(2) この散乱公式は陽電子に対しても正しいことを示せ(行列要素の計算に陽電子状態を用いよ).
問題の解答例は, 次回のブログ記事で書くことにする.解答は W.Greiner : Quantum Electrodynamics の文章を抜粋することで行うつもりである.
References
| ↑1 | [訳註] 運動量移行を \(\mb{q}=\mb{p}_2-\mb{p}_1\) とする.部分積分を2回行い, \(\nabla^{2}e^{-i\mb{q}\cdot\mb{x}}=-\mb{q}^{2}e^{-i\mb{q}\cdot\mb{x}}\) を用いると \begin{align*} V(\mb{q})=Ze^{2}\int\frac{1}{r}e^{-i\mb{q}\cdot\mb{x}}\,d^{3}\mb{x}= -\frac{Ze^{2}}{\mb{q}^{2}} \int \frac{1}{r}\left(\nabla^{2}e^{-i\mb{q}\cdot\mb{x}}\right)\,d^{3}\mb{x} =-\frac{Ze^{2}}{\mb{q}^{2}}\int \left(\nabla^{2}\frac{1}{r}\right)e^{-i\mb{q}\cdot\mb{x}}\,d^{3}\mb{x} \end{align*} さらに \(\displaystyle \nabla^{2}\left(\frac{1}{r}\right)=-4\pi\,\delta^{3}(\mb{x})\) であるから \begin{align*} V(\mb{q})=-\frac{Ze^{2}}{\mb{q}^{2}}\int\bigl\{-4\pi\delta^{3}(\mb{x})\bigr\}e^{-i\mb{q}\cdot\mb{x}}\,d^{3}\mb{x} =\frac{4\pi Ze^{2}}{\mb{q}^{2}} \end{align*} また2番目の時間積分は,その積分区間を原書では \([0,T]\) としているが, ここでは他の教科書に合わせて \([-\infty,\infty]\) とする: \begin{align*} \int_{0}^{T} e^{i (E_2-E_1)t}\,dt=\frac{e^{i(E_2-E_1)T}-1}{i(E_2-E_1)}\quad\rightarrow\quad \int_{-\infty}^{\infty} e^{i(E_2-E_1)t}\,dt =2\pi \delta(E_2-E_1) \end{align*} そのときW.Greiner : QED § 3.1 により次が言える: \begin{align*} \bigl\{2\pi\delta(E_2-E_1)\bigr\}^{2}=2\pi\delta(0)2\pi\delta(E_2-E_1) \stackrel{!}{=} 2\pi T \delta(E_2-E_1) \end{align*} ただし \(=\) の上に!(感嘆符)が付いている記号(\(\overset{!}{=}\))は, 生成AIに聞いたら『主に数学や物理の数式において「定義による等号」や「強調された等しい関係」を意味する』と答えてくれた. |
|---|---|
| ↑2 | [訳註] 始状態 \(i\) から終状態の組 \([n]\) への単位時間あたりの遷移確率 \(w_{i\to [n]}\) は, 一次の摂動まで考慮すると次の「フェルミの黄金則」で与えられる: \begin{align*} w_{i\to [n]}=\frac{2\pi}{\hbar}\overline{\left|V_{ni}\right|}\rho(E_n)_{E_n\simeq E_i} \end{align*} |
| ↑3 | [訳註] 時間積分に由来するこのデルタ関数は最終的に \(1\) になるので, ファインマンはそれを除いたのではないだろうか?.不変振幅などの文章は原書には無く訳者が追加したので注意する. |
| ↑4 | \begin{align*} p_1=\frac{mv_1}{\sqrt{1-v_1^{2}}}\ \rightarrow\ p_1^{2}=\frac{m^{2}v_1^{2}}{1-v_1^{2}}\ \rightarrow\ p_1^{2}(1-v_1^{2})=m^{2}v_1^{2}\ \rightarrow\ p_1^{2}=(m^{2}+p_1^{2})v_1^{2} =E_1^{2}v_1^{2},\quad\text{therfore} \quad v_1=\frac{p_1}{E_1} \end{align*} |
| ↑5 | [訳註] 結果式 (C) をさらに変形すると, \begin{align*} \sigma &=\frac{4Z^{2}e^{4}E^{2}}{\ds{\left(2p\sin\frac{\theta}{2}\right)^{4}}} d\Omega \left[ 1-v^{2}\sin^{2} \frac{\theta}{2}\right] =\frac{Z^{2}e^{4}}{\ds{4p^{2}\left(\frac{p^{2}}{E^{2}}\right)\sin^{4}\frac{\theta}{2}}} \left[ 1-v^{2}\sin^{2} \frac{\theta}{2}\right] =\frac{Z^{2}e^{4}}{\ds{4p^{2}v^{2}\sin^{4}\frac{\theta}{2}}} \left[ 1-v^{2}\sin^{2} \frac{\theta}{2}\right] \end{align*} この前因子は「Rutherford散乱」の式に一致していることに注意する. |