\(\)
Problem 6-5
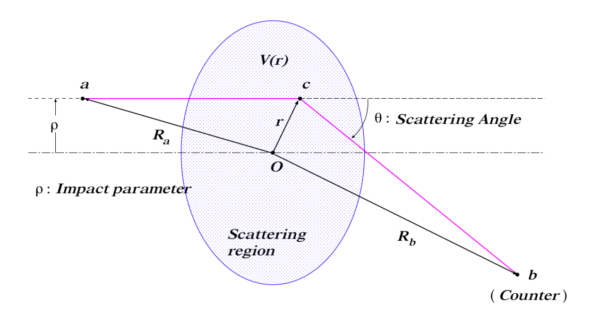
The integral over \(t\) in Eq. (6-28) can be performed approximately using the method of stationary phase. By studying the application of such a method to this integral, show that most of the contribution to the integral comes from values of \(t\) near the region \(t_c=r_a/u\), the time at which the electron would arrive at the center of the atom if it moved in a classical manner.
( 解答 ) まず最初に, M. Born & E. Wolf ：「光学の原理 I」の付録から, 「停留位相法」に関係した部分を抜粋して要約したものを示しておこう．
次の形をした複素積分の漸近近似を得る方法に「最急降下法」( method of steepest descent ) と「停留位相法」(method of stationary phase )がある：
I(s)=\int_C g(z)\,e^{s f(z)}\,dz
\tag{1}
\end{equation}
このとき \(s\) を実数と考えて漸近解を得るのが「最急降下法」である．他方, \(s\) を純虚数 \(ik\) と考えて漸近解を得るのが「停留位相法」であり, その場合 式 (1) は次となる：
I(k)=\int_C g(z)\,e^{i k f(z)}\,dz
\tag{2}
\end{equation}
実際問題では, この指数部は「伝播する波」を表している．このとき, 特に重要な振舞いをするのは,
\frac{d f(z)}{d z} =0
\tag{3}
\end{equation}
を満たす点であり, 「鞍点」( saddle point ) と呼ばれている．
ここで, 指数関数の指数部 \(f(z)\) を次のように表わす：
f(z)=u(x,y)+i v(x,y)
\tag{4}
\end{equation}
このとき, \(f(z)\) が正則関数であるかどうかの決定に用いられる次の「Cauchy-Riemann の関係式」：
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\ppdiff{u}{x}=\ppdiff{v}{y},\quad \ppdiff{u}{y}=-\ppdiff{v}{x}
\tag{5}
\end{equation}
から, 「\(v(x,y)=v_0=\) 一定 である任意の曲線上で, \(u(x,y)\) の変化率がゼロになるのは, 鞍点以外では有り得ない」ことが容易に証明できる．例えば, 第１式を更に \(x\) で微分したものと第２式を更に \(y\) で微分したものを考えると,
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}}
&\pdiff{x}\left(\ppdiff{u}{x}\right)=\Bppdiff{u}{x}=\pdiff{x}\left(\ppdiff{v}{y}\right)
=\frac{\partial^{2}v}{\partial x\partial y}\\
&\pdiff{y}\left(\ppdiff{u}{y}\right)=\Bppdiff{u}{y}=\pdiff{y}\left(-\ppdiff{v}{x}\right)=-\frac{\partial^{2}v}{\partial y\partial x}=-\frac{\partial^{2}v}{\partial x\partial y}\\
&\rightarrow\quad \Bppdiff{u}{x}=-\Bppdiff{u}{y}\quad\rightarrow\quad \Bppdiff{u}{x}+\Bppdiff{u}{y}=0
\end{align}
\(v\) についても同様なことが言える．従って, \(u\) 及び \(v\) は共に次の「プラス方程式」を満たすべきである：
\nabla^{2} u = \Bppdiff{u}{x}+\Bppdiff{u}{y}=0,\quad \nabla^{2} v = \Bppdiff{v}{x}+\Bppdiff{v}{y}=0
\tag{6}
\end{equation}
上式 (6) に於いて, もし \(x\) についての 2 次微分が正ならば, \(y\) についての 2 次微分は負になることが分かる．従って \(u\) も \(v\) も, 絶対的な最大値または最小値を取ることは不可能である．( 例えば, \(u\) が \(x\) 方向に於いて \(u^{”} > 0\) で下に凸ならば, \(y\) 方向では \(u^{”}<0\) なので上に凸となる )．また, 関数 \(f(z)\) は解析的で特異点は排除されている．よって, 式 (3) の微分がゼロとなる点は「鞍点」すなわち「停留値」となるべきである．(この故に, この方法は「停留位相法」と呼ばれ, また, 最急降下法は「鞍点法」とも呼ばれるのである)．
図 1. 関数 \(f(x,y)=x^{2}-1.5*y^{2}\) の原点 \((0,0)\) は鞍点である．
そこで「\(v(x,y)=v_0=\)一定」 の積分路を用いる．すると式 (2) の積分は, 次のように書くことが出来る：
I(s)=\int_C g(z)\,e^{-v}\,e^{i k u}\,dz
\tag{7}
\end{equation}
このとき, 指数部の振幅 \(e^{-v}\) は積分路に沿って一定であるが, 位相 \(e^{i k u}\) は極めて速く変化する (最急降下法では逆になる)．この積分路上で, 積分にハッキリと寄与するのは「鞍点」または端点の付近のみであることが言えるが, その物理的な解釈としては, 振幅の減衰というよりも「位相の干渉 (phase interference)である」と考えられる．その結果, 式 (2) の \(I(k)\) は式 (3) の \(d f/dz=0\) を満たす鞍点の近傍での積分によって近似出来ることになる．「光学の原理 II」の § 8.3.3 Kirchhoff の回折理論 には, 次のように説明されている：
完全に単色なスカラー波 \(V(x,y,z,t)=U(x,y,z)e^{i\omega t}\) が点 \(P_0\) から射出され, 平面状の不透明なスクリーン上の開口に向かって伝搬し通過した波を点 \(P\) で観測するものとする．ただし開口の大きさは波長に比べれば十分に大きいが, スクリーンから射出点および観測点までの距離と比較すると十分に小さいとする．このとき, 観測点での回折波の振幅の式は, 開口 \(\mathscr{A}\) 内の点 \(Q\) の座標を \((\xi,\tau)\) とすれば次式で近似される：
\begin{equation}
U(P)\approx -\frac{i\cos\delta}{\lambda}\frac{A e^{ik(r’+s’)}}{r’s’}\iint_{\mathscr{A}} e^{i k f(\xi,\tau)}\,d\xi d\tau
\tag{28}
\end{equation}
ただし \(r’\) と \(s’\) は, 開口内に設置した座標の原点 \(O\) と点 \(P_0\) 及び \(P\) との距離である．この式に於いて, 点 \((\xi,\tau)\) が積分範囲内で動く時, 関数 \(f(\xi,\tau)\) の変化は波長に比べてはるかに大きいため, 積分の実部および虚数部は符号変化を多数行う．その結果として, 一般に, 微小面積間で互いに打ち消し合う．しかしながら, \(f(\xi,\tau)\) が停留的な値を取る点 ( 臨界点または極 ) の付近では事情は異なり, 被積分関数は非常にゆっくりと変化するため, 積分への寄与がある程度期待される．すなわち, 波長が十分に小さいとすれば, \(f\) が停留的な値を取る点の付近で \(f\) がどのように振舞うかによって, 積分は実質的に決定される．これが, ある種の積分の漸近的な振舞いを決定する「停留位相法」の原理である．
次に, 停留位相法により「式 (6-28) の \(t\)-積分について, その積分に寄与するのは大部分が時間 \(t_c=R_a/u\) の近傍から来ること」を示す．ただし, 本文から \(u\) は電子の速度であり \(u=(R_a+R_b)/T\) である．
式 (6-28) の \(t\) についての積分部分は次である：
\def\mb#1{\mathbf{#1}}
I(t)&=\int_0^{T}dt\,\left(\frac{m}{2\pi i\hbar(T-t)}\right)^{3/2}\left(\frac{m}{2\pi i\hbar t}\right)^{3/2}
\exp\left[\frac{im|\mb{R}_b-\mb{r}|^{2}}{2\hbar(T-t)}\right]\,\exp\left[\frac{im|\mb{R}_a-\mb{r}|^{2}}{2\hbar t}\right]\\
&=\left(\frac{m}{2\pi i\hbar}\right)^{3}\int_0^{T}\frac{1}{\bigl[(T-t)t\bigr]^{3/2}}\,\exp\left[\frac{im}{2\hbar}
\left\{\frac{|\mb{R}_a-\mb{r}|^{2}}{t}-\frac{|\mb{R}_b-\mb{r}|^{2}}{t-T}\right\}\right]\,dt
\tag{8}
\end{align}
この指数因子の位相部分から定数 \(im/2\hbar\) を除いた部分を \(f(t)\) とする：
f(t)=\frac{|\mb{R}_a-\mb{r}|^{2}}{t}-\frac{\mb{R}_b-\mb{r}|^{2}}{t-T}\equiv \frac{r_a^{2}}{t}-\frac{r_b^{2}}{t-T}
\tag{9}
\end{equation}
定数位相法に従って, 関数 \(f(t)\) を \(t\) で微分したものをゼロとする：
&\frac{d f(t)}{dt}=-\frac{r_a^{2}}{t^{2}}+\frac{r_b^{2}}{(t-T)^{2}}=0,\\
&\rightarrow\quad (r_b^{2}-r_a^{2})t^{2}+2r_a^{2}Tt-r_a^{2}T^{2}=0
\tag{10}
\end{align}
この変数 \(t\) についての 2 次方程式の「根と係数の関係」を用いて, 条件を満たす \(t=t_c\) を求めると ( 明らかに符号は + とすべきである),
t_c&=\frac{-r_a^{2}T+\sqrt{r_a^{4}T^{2}+(r_b^{2}-r_a^{2})r_a^{2}T^{2}}}{r_b^{2}-r_a^{2}}=\frac{-r_a^{2}T+r_ar_bT}{r_b^{2}-r_a^{2}}\\
&=\frac{r_aT}{r_b+r_a}=\frac{r_a}{(r_a+r_b)/T}=\frac{r_a}{u}\simeq \frac{R_a}{u}
\tag{11}
\end{align}
従って, 積分の寄与の大部分は時間 \(t_c=R_a/u\) の近傍から由来することが示された．この \(R_a\) は粒子の出発位置 \(a\) と散乱領域の位置 \(c\) との距離 \(r_a\) にほぼ等しいので, この時間 \(t_c\) は「電子が古典的に運動して原子の散乱中心 (原子核) に到達する時間」であると言える．
図 2. 散乱問題の幾何学．電子は \(a\) から出発して自由粒子として運動し \(c\) に到る．\(c\) では原子ポテンシ ャル \(V(r)\) によって散乱される．散乱の後に \(b\) にある計測器に到る．\(b\) は散乱中心 \(O\) から動径ベクトル \(\mb{R}_b\) の所に位置している．この散乱過程で電子は, 非散乱電子線の方向から測って角度 \(\theta\) だけ散乱される．この過程は第 1 次ボルン近似に対応する．2 回の散乱 (散乱の起こる位置を \(c,d\) とする) に対する振幅を含める場合, その結果は第 2 次近似である, 等々となる．
