問題 8-6 の解答例

Problem 8-6
Show that the constants $a_{j α}$ are the same even if the coupling is not just to the nearest neighbors but extends with strengths $λ_{k}$ to atoms $k$ spaces away. Assuming $λ_{k}$ falls rapidly enough for large $k$ , find the values of the frequency $ω_{α}$ when such a coupling is present, i.e., when the potential energy, instead of being given by Eq. (8-66), is given by a similar equation, but one which contains the relative displacements of all pairs of atoms, each one multiplied by the appropriate $λ_{k}$ , that is,

V = \frac{ν^{2}}{2} \sum_{j} \sum_{k} λ_{k} (q_{k + j} - q_{j})^{2}

( 解答 )　この問題に類似したものが, アシュクロフト・マーミン：「個体物理の基礎」第22章の演習問題１に存在し, そこに示されている「分散関係」は次のようになっている：

\begin{matrix} (1) & ω = 2 \sqrt{\sum_{m > 0} \frac{K_{m}}{M} \sin^{2} \frac{m k a}{2}} \end{matrix}

まず, この場合の式 (8-67) に相当するラグランジアンは次となる：

\begin{matrix} (2) & L = T - V = \sum_{j = 1}^{N} \frac{1}{2} {\dot{q}}_{j}^{2} - \frac{ν^{2}}{2} \sum_{j = 1}^{N} \sum_{k = 1}^{M} λ_{k} (q_{j + k} - q_{j})^{2} \end{matrix}

このとき,

k

の範囲は

M

個までとしよう．ただし

M < N / 2

である．すると,

\begin{matrix} (3) & p_{l} = \frac{\partial L}{\partial {\dot{q}}_{l}} = \frac{\partial}{\partial {\dot{q}}_{l}} (\sum_{j = 1}^{N} \frac{1}{2} {\dot{q}}_{j}^{2}) = {\dot{q}}_{l} \end{matrix}

また, ラグランジュの運動方程式から,

\begin{matrix} (4) & \frac{d}{d t} \frac{\partial L}{\partial {\dot{q}}_{l}} - \frac{\partial L}{\partial q_{l}} = 0 \to {\dot{p}}_{l} = \frac{d}{d t} (\frac{\partial L}{\partial {\dot{q}}_{l}}) = \frac{\partial L}{\partial q_{l}} \end{matrix}

式 (3) と式 (4) とから,

\begin{aligned} {\dot{p}}_{l} & = {\ddot{q}}_{l} = \frac{\partial L}{\partial q_{l}} = \frac{\partial}{\partial q_{l}} {- \frac{ν^{2}}{2} \sum_{j} \sum_{k} λ_{k} (q_{j + k} - q_{j})^{2}} \\ = - \frac{ν^{2}}{2} \sum_{j} \sum_{k} λ_{k} \frac{\partial}{\partial q_{l}} (q_{j + k}^{2} - 2 q_{j + k} q_{j} + q_{j}^{2}) \\ (5) & = - \frac{ν^{2}}{2} \sum_{j = 1}^{N} \sum_{k = 1}^{M} λ_{k} {2 q_{j + k} δ_{j + k, l} - 2 q_{j} δ_{j + k, l} - 2 q_{j + k} δ_{j, l} + 2 q_{j} δ_{j, l}} \end{aligned}

従って, 式 (8-68) に相当する式として次が得られる：

\begin{aligned} {\dot{p}}_{l} = {\ddot{q}}_{l} & = - ν^{2} \sum_{k} λ_{k} q_{l} + ν^{2} \sum_{k} λ_{k} q_{l - k} + ν^{2} \sum_{k} λ_{k} q_{l + k} - ν^{2} \sum_{k} λ_{k} q_{l} \\ = ν^{2} \sum_{k} λ_{k} (q_{l - k} - q_{l}) + ν^{2} \sum_{k} λ_{k} (q_{l + k} - q_{l}) \\ (6) & \to {\ddot{q}}_{l} & = ν^{2} \sum_{k} λ_{k} [(q_{l + k} - q_{l}) - (q_{l} - q_{l - k})] = ν^{2} \sum_{k = 1}^{M} λ_{k} (q_{l + k} - 2 q_{l} + q_{l - k}) \end{aligned}

すると, 式 (8-70) に相当する式は次となる：

\begin{matrix} (7) & {\ddot{q}}_{j} = - ω^{2} q_{j} = ν^{2} \sum_{k = 1}^{M} λ_{k} (q_{j + k} - 2 q_{j} + q_{j - k}) \end{matrix}

この方程式 (7) の解は, 静止しているときの原子間隔を

b

として式 (8-71) を多少修正したものとしよう．すると,

j

番目原子の平衡位置からの変位

q_{j}

は次となる：

\begin{aligned} (8) & q_{j} & = A e^{i (K b j - ω t)} = A e^{i K b j} e^{- i ω t} \equiv a_{j} e^{- i ω t} \\ \to q_{j + k} & = A e^{i (K b j + K b k - ω t)} = e^{i K b k} q_{j}, q_{j - k} = A e^{i (K b j - K b k - ω t)} = e^{- i K b k} q_{j} \end{aligned}

式 (8) を式 (7) に代入すると,

\begin{aligned} - ω^{2} q_{j} & = ν^{2} \sum_{k = 1}^{M} λ_{l} (q_{j + k} - 2 q_{j} + q_{j - k}) = ν^{2} \sum_{k} λ_{k} (e^{i K b k} q_{j} - 2 q_{j} + e^{- i K b k} q_{j}) \\ = ν^{2} q_{j} \sum_{k} λ_{k} (e^{i K b k} - 2 + e^{- i K b k}) \end{aligned}

従って,

ω

が満たすべき式として次が得られる：

\begin{aligned} (9) & ω^{2} & = - ν^{2} \sum_{k} λ_{k} (e^{i K b k} - 2 + e^{- i K b k}) = 4 ν^{2} \sum_{k = 1}^{M} λ_{k} \sin^{2} (\frac{K b k}{2}), \\ (10) & \to ω & = 2 ν {| \sum_{k = 1}^{M} λ_{k} \sin^{2} (\frac{K b k}{2}) |}^{1 / 2} \end{aligned}

この分散関係の概略 (ただし

λ_{1} = 1, λ_{2} = 1 / 2, λ_{3} = 1 / 4

とした場合) を図示すると次の図 1 のようになる．また, アシュクロフト・マーミンの第２４章に「中性子散乱によって測定したアルミニウムのフォノン分散関係」の図 24.2 があったので参考のために示しておく(図 2)：

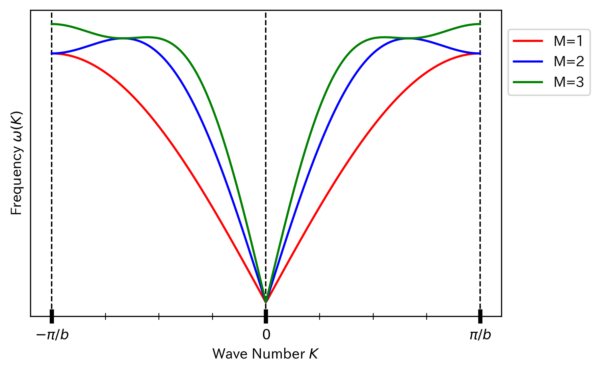
図 1. $M$ 番目まで隣接相互作用がある 1 次元鎖の分散関係．ただし $λ_{1} = 1, λ_{2} = 0.5, λ_{3} = 0.25$ ．

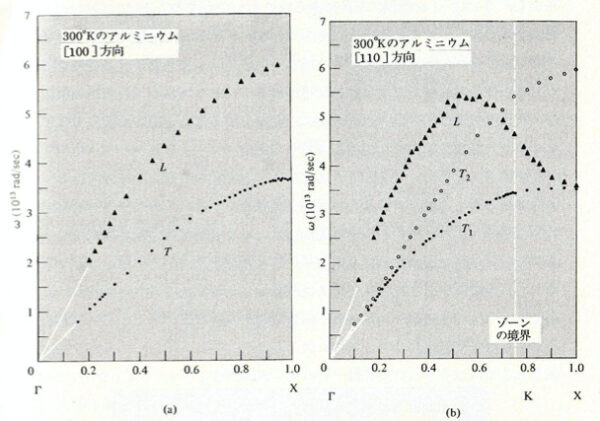
図 2. 中性子散乱によって測定したアルミニウムのフォノン分散関係 (アシュクロフト・マーミン：「個体物理の基礎」による)．

この式 (10) は, 以下のように置き換えるならば, アシュクロフト・マーミンに与えられている式 (1) に相当したものになっている!：

k \to m, K \to k, b \to a, ν^{2} λ_{k} \to \frac{K_{m}}{M}

更に, ここでは周期的境界条件：

q_{j + N} = q_{j}

から, 式 (9) の

K

の値は

K = 2 π α / N b

だけが許される．従って,

ω_{α}

についての式は,

\begin{matrix} (11) & ω_{α}^{2} = 4 ν^{2} \sum_{k = 1}^{M} λ_{k} \sin^{2} (\frac{b k}{2} \cdot \frac{2 π α}{N b}) = 4 ν^{2} \sum_{k = 1}^{M} λ_{k} \sin^{2} (\frac{π k}{N} α) \end{matrix}

よって, 式 (10) は次のように書くことが出来る：

\begin{matrix} (12) & ω_{α} = 2 ν {| \sum_{k = 1}^{M} λ_{k} \sin^{2} (\frac{π k}{N} α) |}^{1 / 2}, where α = 0, 1, 2, \dots, (N - 1) \end{matrix}

更に, このときの振動数

ω_{α}

に対する

j

番目座標の振幅

a_{j α}

は, 式 (8-74) と同じ形で書けることに注意する：

\begin{matrix} (13) & a_{j α} = A e^{i K b j} = A \exp (i \frac{2 π α}{N b} b j) = A \exp (i \frac{2 π}{N} j α) \end{matrix}

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31