\(\)
少し前後するけれども, 本文の「最小作用の原理」に式の導出などを補足しておくことにする．
最小作用の原理
量子電磁力学の仮説は,「式(9-21)と式(9-22)で定義される振動子が量子的振動子である」ということである：
\begin{align}
\def\mb#1{\mathbf{#1}}
&\ddot{\mb{a}}_{\mb{k}}(t)+k^{2}c^{2}\mb{a}_{\mb{k}}(t)=\sqrt{4\pi}\,\mb{j}’_{\mb{k}}(t),\quad \mb{j}’_{\mb{k}}(t)=\mb{j}_{\mb{k}}(t)-\frac{\mb{k}}{k^{2}}\{\mb{k}\cdot\mb{j}_{\mb{k}}(t)\}
\tag{9-20}\\
\rightarrow\quad&\quad \ddot{a}_{1\mb{k}}+k^{2}c^{2}a_{1\mb{k}}=\sqrt{4\pi}\,j_{1\mb{k}}(t)
\tag{9-21}\\
\quad&\quad \ddot{a}_{2\mb{k}}+k^{2}c^{2}a_{2\mb{k}}=\sqrt{4\pi}\,j_{2\mb{k}}(t)
\tag{9-22}
\end{align}
\def\mb#1{\mathbf{#1}}
&\ddot{\mb{a}}_{\mb{k}}(t)+k^{2}c^{2}\mb{a}_{\mb{k}}(t)=\sqrt{4\pi}\,\mb{j}’_{\mb{k}}(t),\quad \mb{j}’_{\mb{k}}(t)=\mb{j}_{\mb{k}}(t)-\frac{\mb{k}}{k^{2}}\{\mb{k}\cdot\mb{j}_{\mb{k}}(t)\}
\tag{9-20}\\
\rightarrow\quad&\quad \ddot{a}_{1\mb{k}}+k^{2}c^{2}a_{1\mb{k}}=\sqrt{4\pi}\,j_{1\mb{k}}(t)
\tag{9-21}\\
\quad&\quad \ddot{a}_{2\mb{k}}+k^{2}c^{2}a_{2\mb{k}}=\sqrt{4\pi}\,j_{2\mb{k}}(t)
\tag{9-22}
\end{align}
ただし \(j_{1\mb{k}}\) と \(j_{2\mb{k}}\) は, これらの方向の \(\mb{j}_k\) の成分である．このとき, なぜ「\(\mb{j}_{\mb{k}}’\) の成分」と言う必要がないのだろうか？．
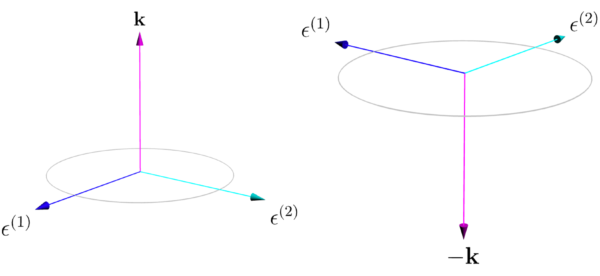
「偏極ベクトル(polarization vector) を \(\mb{\epsilon}^{(\alpha)} (\alpha=1,2)\) としたとき, 単位ベクトルであるこの偏極ベクトルは, \(\mb{k}\) が与えられると \((\mb{\epsilon}^{(1)},\mb{\epsilon}^{(2)},\mb{k})\) が右手系を構成する基底ベクトルの組になるように \(\mb{\epsilon}^{(1)}\) と \(\mb{\epsilon}^{(2)}\) が選ばれる．\(\mb{\epsilon}^{(\alpha)}\) は伝播方向 \(\mb{k}\) と直交しているので「横波条件」が保証される：\(\mb{\epsilon}^{(\alpha)}\cdot\mb{k}=0\)．従って, 式 (9.20) の両辺に \(\mb{\epsilon}^{(\alpha)}\) をかけ合わせると,
\begin{equation}
\mb{\epsilon}^{(\alpha)}\cdot\mb{j}’_{\mb{k}}(t)\equiv j’_{\alpha \mb{k}}(t)
=\mb{\epsilon}^{(\alpha)}\cdot\mb{j}_{\mb{k}}(t)
-\frac{\mb{\epsilon}^{(\alpha)}\cdot\mb{k}}{k^{2}}\{\mb{k}\cdot\mb{j}_{\mb{k}}(t)\}
=\mb{\epsilon}^{(\alpha)}\cdot\mb{j}_{\mb{k}}(t)\equiv j_{\alpha \mb{k}}(t)
\end{equation}
\mb{\epsilon}^{(\alpha)}\cdot\mb{j}’_{\mb{k}}(t)\equiv j’_{\alpha \mb{k}}(t)
=\mb{\epsilon}^{(\alpha)}\cdot\mb{j}_{\mb{k}}(t)
-\frac{\mb{\epsilon}^{(\alpha)}\cdot\mb{k}}{k^{2}}\{\mb{k}\cdot\mb{j}_{\mb{k}}(t)\}
=\mb{\epsilon}^{(\alpha)}\cdot\mb{j}_{\mb{k}}(t)\equiv j_{\alpha \mb{k}}(t)
\end{equation}
よって, 成分 \(j’_{\alpha \mb{k}}(t)\) と成分 \(j_{\alpha \mb{k}}(t)\) は一致することになるからである」．
図 1. 偏極ベクトル
量子化を実行するために, 場の運動方程式と場の中の粒子の運動方程式を与える最小作用の原理を見つけなければならない．作用は次のように表わされる： [1]式 (9-24) から式 (9-26) … Continue reading
\begin{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
S=S_1+S_2+S_3
\tag{9-23}
\end{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
S=S_1+S_2+S_3
\tag{9-23}
\end{equation}
ここで, \(S_1\) は「場を無視したときの全粒子の作用積分」である (粒子間に電気的でない力が働く場合は, それを \(S_1\) に含める)：
\begin{equation}
S_1=\int dt\int d^{3}\mb{r}\,\sum_i \frac{m_i}{2}|\dot{\mb{r}}|^{2}\,\delta^{3}(\mb{r}-\mb{q}_i)
=\int dt\,\sum_i \frac{m_i}{2}\,|\dot{\mb{q}}_i|^{2}
\tag{9-24}
\end{equation}
S_1=\int dt\int d^{3}\mb{r}\,\sum_i \frac{m_i}{2}|\dot{\mb{r}}|^{2}\,\delta^{3}(\mb{r}-\mb{q}_i)
=\int dt\,\sum_i \frac{m_i}{2}\,|\dot{\mb{q}}_i|^{2}
\tag{9-24}
\end{equation}
また, \(S_2\) は「場と粒子間の相互作用を表わす作用積分」である：
\begin{equation}
S_2=-\int dt\int d^{3}\mb{r}\,\left[\rho(\mb{r},t)\,\phi(\mb{r},t)-\reverse{c}\mb{j}(\mb{r},t)\cdot
\mb{A}(\mb{r},t)\right]
\tag{9-25}
\end{equation}
S_2=-\int dt\int d^{3}\mb{r}\,\left[\rho(\mb{r},t)\,\phi(\mb{r},t)-\reverse{c}\mb{j}(\mb{r},t)\cdot
\mb{A}(\mb{r},t)\right]
\tag{9-25}
\end{equation}
そして \(S_3\) は「場の作用積分」である．変数は \(\mb{A}(\mb{r},t)\), \(\phi(\mb{r},t)\), \(\mb{q}_i(t)\) である：
\begin{align}
S_3&=\reverse{8\pi}\int dt\int d^{3}\mb{r}\,(E^{2}-B^{2})\notag\\
&=\reverse{8\pi}\int dt\int d^{3}\mb{r}\,
\left[\,\left|-\nabla\phi-\reverse{c}\ppdiff{\mb{A}}{t}\right|^{2}-|\nabla\times\mb{A}|^{2}\right]
\tag{9-26}
\end{align}
S_3&=\reverse{8\pi}\int dt\int d^{3}\mb{r}\,(E^{2}-B^{2})\notag\\
&=\reverse{8\pi}\int dt\int d^{3}\mb{r}\,
\left[\,\left|-\nabla\phi-\reverse{c}\ppdiff{\mb{A}}{t}\right|^{2}-|\nabla\times\mb{A}|^{2}\right]
\tag{9-26}
\end{align}
変数 \(\mb{a}_k\) を使うと, 運動方程式が最も簡単になるので, 作用をこれらの変数で表してみることは価値がある．式(9-14)の展開を \(S_3\) に代入すると, 次が得られる：
\begin{align}
S_3&=\reverse{2}\int dt \int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(\,\left|\dot{\mb{a}}_k+i\mb{k}
\frac{\phi_k}{\sqrt{4\pi}}\right|^{2}-c^{2}|\mb{k}\times\mb{a}_k|^{2}\,\right)\notag\\
&=\reverse{2}\int dt \int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(\,\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k
+\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k-k^{2}c^{2}\mb{a}_k^{*}\cdot\mb{a}_k\,\right)
\tag{9-27}
\end{align}
S_3&=\reverse{2}\int dt \int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(\,\left|\dot{\mb{a}}_k+i\mb{k}
\frac{\phi_k}{\sqrt{4\pi}}\right|^{2}-c^{2}|\mb{k}\times\mb{a}_k|^{2}\,\right)\notag\\
&=\reverse{2}\int dt \int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(\,\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k
+\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k-k^{2}c^{2}\mb{a}_k^{*}\cdot\mb{a}_k\,\right)
\tag{9-27}
\end{align}
そして \(S_2\) は次となる：
\begin{equation}
S_2=-\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(\rho_{-k}\phi_k-\sqrt{4\pi}\,\mb{j}_{-k}\cdot\mb{a}_k
\Bigr)
\tag{9-28}
\end{equation}
S_2=-\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(\rho_{-k}\phi_k-\sqrt{4\pi}\,\mb{j}_{-k}\cdot\mb{a}_k
\Bigr)
\tag{9-28}
\end{equation}
上式に \(\phi_k=4\pi\rho_k/k^{2}\) を代入し, \(S_2\) と \(S_3\) に在る \(\phi_k\) の項を足し合わせることで次が得られる：
\begin{equation}
S_c=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(-\frac{4\pi\rho_k\rho_{-k}}{2k^{2}}\right)
=\int dt\,\left[\,-\reverse{2}\sum_i\sum_j \frac{e_ie_j}{|\mb{q}_i-\mb{q}_j|}\,\right]
\tag{9-29}
\end{equation}
S_c=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(-\frac{4\pi\rho_k\rho_{-k}}{2k^{2}}\right)
=\int dt\,\left[\,-\reverse{2}\sum_i\sum_j \frac{e_ie_j}{|\mb{q}_i-\mb{q}_j|}\,\right]
\tag{9-29}
\end{equation}
ただし式 (9-16} 並びに \(\displaystyle{\int d^{3}\mb{k}\frac{4\pi}{k^{2}}e^{i\mb{k}\cdot\mb{r}}=\reverse{r}}\) を用いた．この \(S_c\) はまさに,「電荷の間のクーロン相互作用」である．クーロン相互作用を考えるのは通常, 電磁場の放射効果を無視して原子状態を解析するときである． (このとき, \(S_2+S_3=S_c+S_{rad}+S_{int}\) となる)．
【 補助メモ 】 まず \(E^{2}\) と \(B^{2}\) を, 式(9-17)の前に書かれている \(\mb{E}_{\mb{k}},\,\mb{B}_{\mb{k}}\) の式
\begin{equation}
\mb{E}_{\mb{k}}=-i\mb{k}\phi_{\mb{k}}-\sqrt{4\pi}\,\dot{\mb{a}}_{\mb{k}},\quad
\mb{B}_{\mb{k}}=\sqrt{4\pi}\,c i\,(\mb{k}\times\mb{a}_{\mb{k}})
\tag{1}
\end{equation}
\mb{E}_{\mb{k}}=-i\mb{k}\phi_{\mb{k}}-\sqrt{4\pi}\,\dot{\mb{a}}_{\mb{k}},\quad
\mb{B}_{\mb{k}}=\sqrt{4\pi}\,c i\,(\mb{k}\times\mb{a}_{\mb{k}})
\tag{1}
\end{equation}
を用いて表してみると,
\begin{align}
E^{2}&=\mb{E}^{*}\cdot\mb{E}=\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,e^{-i\mb{k}’\cdot\mb{r}}(i\mb{k}\phi_{k’}^{*}-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)\\
&=\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,(i\mb{k}\phi_{k’}^{*}
-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)
\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}\tag{2}\\
B^{2}&=\mb{B}^{*}\cdot\mb{B}=\int \frac{d^{3}\mb{k}^{‘}}{(2\pi)^{3}}\,e^{-i\mb{k}’\cdot\mb{r}}\sqrt{4\pi}
\{-ic(\mb{k}’\times\mb{a}_{k’}^{*})\}\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}
\sqrt{4\pi}ci(\mb{k}\times\mb{a}_k)\\
&=\int \frac{d^{3}\mb{k}^{‘}}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,4\pi c^{2}
(\mb{k}’\times\mb{a}_{k’}^{*})\cdot(\mb{k}\times\mb{a}_k)\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}
\tag{3}
\end{align}
E^{2}&=\mb{E}^{*}\cdot\mb{E}=\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,e^{-i\mb{k}’\cdot\mb{r}}(i\mb{k}\phi_{k’}^{*}-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)\\
&=\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,(i\mb{k}\phi_{k’}^{*}
-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)
\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}\tag{2}\\
B^{2}&=\mb{B}^{*}\cdot\mb{B}=\int \frac{d^{3}\mb{k}^{‘}}{(2\pi)^{3}}\,e^{-i\mb{k}’\cdot\mb{r}}\sqrt{4\pi}
\{-ic(\mb{k}’\times\mb{a}_{k’}^{*})\}\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,e^{i\mb{k}\cdot\mb{r}}
\sqrt{4\pi}ci(\mb{k}\times\mb{a}_k)\\
&=\int \frac{d^{3}\mb{k}^{‘}}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}}{(2\pi)^{3}}\,4\pi c^{2}
(\mb{k}’\times\mb{a}_{k’}^{*})\cdot(\mb{k}\times\mb{a}_k)\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}
\tag{3}
\end{align}
従って式 (9-26) の \(S_3\) は, \(\delta\) -関数の性質を利用して次に書ける：
\begin{align}
S_3&=\reverse{8\pi}\int dt\int d^{3}\mb{r}\,(E^{2}-B^{2})=\int dt\reverse{8\pi}\int d^{3}\mb{r}\,E^{2}-\int dt\reverse{8\pi}\int d^{3}\mb{r}\,B^{2}\\
&=\int dt\reverse{8\pi}\int \frac{d^{3}\mb{k}^{‘}}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,(i\mb{k}\phi_{k’}^{*}-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)\,\int d^{3}\mb{r}\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}\\
&\quad-\int dt\reverse{8\pi}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,4\pi c^{2}(\mb{k}’\times\mb{a}_{k’}^{*})\cdot(\mb{k}\times\mb{a}_k)\,\int d^{3}\mb{r}\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}\\
&=\int dt\reverse{8\pi}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,(i\mb{k}\phi_{k’}^{*}-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)\,(2\pi)^{3}\,\delta^{3}(\mb{k}-\mb{k}’)\\
&\quad-\int dt\reverse{8\pi}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,4\pi c^{2}(\mb{k}’\times\mb{a}_{k’}^{*})\cdot(\mb{k}\times\mb{a}_k)
\,(2\pi)^{3}\,\delta^{3}(\mb{k}-\mb{k}’)\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\reverse{2}\left(\dot{\mb{a}}_k^{*}
-\frac{i\mb{k}}{\sqrt{4\pi}}\phi_k^{*}\right)\left(\dot{\mb{a}}_k
+\frac{i\mb{k}}{\sqrt{4\pi}}\phi_k\right)
-\int dt\reverse{8\pi}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}
\,4\pi c^{2}(\mb{k}\times\mb{a}_k^{*})\cdot(\mb{k}\times\mb{a}_k)\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\reverse{2}\left|\dot{\mb{a}}_k+\frac{i\mb{k}}{\sqrt{4\pi}}\phi_k\right|^{2}
-\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\frac{c^{2}}{2}|\mb{k}\times\mb{a}_k|^{2}\\
&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left(\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k+
\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k-c^{2}|\mb{k}\times\mb{a}_k|^{2}\right)
\tag{4}
\end{align}
S_3&=\reverse{8\pi}\int dt\int d^{3}\mb{r}\,(E^{2}-B^{2})=\int dt\reverse{8\pi}\int d^{3}\mb{r}\,E^{2}-\int dt\reverse{8\pi}\int d^{3}\mb{r}\,B^{2}\\
&=\int dt\reverse{8\pi}\int \frac{d^{3}\mb{k}^{‘}}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,(i\mb{k}\phi_{k’}^{*}-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)\,\int d^{3}\mb{r}\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}\\
&\quad-\int dt\reverse{8\pi}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,4\pi c^{2}(\mb{k}’\times\mb{a}_{k’}^{*})\cdot(\mb{k}\times\mb{a}_k)\,\int d^{3}\mb{r}\,e^{i(\mb{k}-\mb{k}’)\cdot\mb{r}}\\
&=\int dt\reverse{8\pi}\int \frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,(i\mb{k}\phi_{k’}^{*}-\sqrt{4\pi}\dot{\mb{a}}_{k’}^{*})(-i\mb{k}\phi_k-\sqrt{4\pi}\dot{\mb{a}}_k)\,(2\pi)^{3}\,\delta^{3}(\mb{k}-\mb{k}’)\\
&\quad-\int dt\reverse{8\pi}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,4\pi c^{2}(\mb{k}’\times\mb{a}_{k’}^{*})\cdot(\mb{k}\times\mb{a}_k)
\,(2\pi)^{3}\,\delta^{3}(\mb{k}-\mb{k}’)\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\reverse{2}\left(\dot{\mb{a}}_k^{*}
-\frac{i\mb{k}}{\sqrt{4\pi}}\phi_k^{*}\right)\left(\dot{\mb{a}}_k
+\frac{i\mb{k}}{\sqrt{4\pi}}\phi_k\right)
-\int dt\reverse{8\pi}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}
\,4\pi c^{2}(\mb{k}\times\mb{a}_k^{*})\cdot(\mb{k}\times\mb{a}_k)\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\reverse{2}\left|\dot{\mb{a}}_k+\frac{i\mb{k}}{\sqrt{4\pi}}\phi_k\right|^{2}
-\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\frac{c^{2}}{2}|\mb{k}\times\mb{a}_k|^{2}\\
&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left(\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k+
\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k-c^{2}|\mb{k}\times\mb{a}_k|^{2}\right)
\tag{4}
\end{align}
ここで被積分関数の第2項は, ベクトル解析の公式 \((\mb{a}\times\mb{b})\cdot(\mb{c}\times\mb{d})
=(\mb{a}\cdot\mb{c})(\mb{b}\cdot\mb{d})-(\mb{a}\cdot\mb{d})(\mb{b}\cdot\mb{c})\) と, 式 (9-13) の \(\mb{k}\cdot\mb{a}_k=0\) を用いると次に変形できる：
\begin{equation}
|\mb{k}\times\mb{a}_k|^{2}=(\mb{k}\times\mb{a}_k^{*})\cdot(\mb{k}\times\mb{a}_k)
=(\mb{k}\cdot\mb{k})(\mb{a}_k^{*}\cdot\mb{a}_k)-(\mb{k}\cdot\mb{a}_k)(\mb{a}_k^{*}\cdot\mb{k})
=k^{2}(\mb{a}_k^{*}\cdot\mb{a}_k)=k^{2}|\mb{a}_k|^{2}
\tag{5}
\end{equation}
|\mb{k}\times\mb{a}_k|^{2}=(\mb{k}\times\mb{a}_k^{*})\cdot(\mb{k}\times\mb{a}_k)
=(\mb{k}\cdot\mb{k})(\mb{a}_k^{*}\cdot\mb{a}_k)-(\mb{k}\cdot\mb{a}_k)(\mb{a}_k^{*}\cdot\mb{k})
=k^{2}(\mb{a}_k^{*}\cdot\mb{a}_k)=k^{2}|\mb{a}_k|^{2}
\tag{5}
\end{equation}
従って \(S_3\) は次のように書くことも出来る：
\begin{equation}
S_3=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left(\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k+
\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k-c^{2}k^{2}\mb{a}_k^{*}\cdot\mb{a}_k\right)
\tag{6}
\end{equation}
S_3=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left(\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k+
\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k-c^{2}k^{2}\mb{a}_k^{*}\cdot\mb{a}_k\right)
\tag{6}
\end{equation}
次に \(S_2\) を, 同様に式 (9-25) に式 (9-14) を代入して求めるならば次となる：
\begin{align}
S_2&=-\int dt\int d^{3}\mb{r}\,\left[\rho(\mb{r},t)\phi(\mb{r},t)-\reverse{c}\mb{j}(\mb{r},t)\cdot
\mb{A}(\mb{r},t)\right],\\
\int d^{3}\mb{r}\,\rho\,\phi&=\int d^{3}\mb{r}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,\rho_{k’}(t)\,e^{i\mb{k}’\cdot\mb{r}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_k(t)
\,e^{i\mb{k}\cdot\mb{r}}\\
&=\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{k’}(t)\,
\phi_k(t)\int d^{3}\mb{r}\,e^{i(\mb{k}’+\mb{k})\cdot\mb{r}}\\
&=\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{k’}(t)\,
\phi_k(t)\,(2\pi)^{3}\delta^{3}(\mb{k}’+\mb{k})\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{-k}(t)\,\phi_k(t),\\
\reverse{c}\int d^{3}\mb{r}\,\mb{j}\cdot\mb{A}&=\reverse{c}\int d^{3}\mb{r}\,\left(\int
\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,\mb{j}_{k’}(t)\,e^{i\mb{k}’\cdot\mb{r}}\right)\cdot
\left(\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\mb{a}_k(t)\,e^{i\mb{k}\cdot\mb{r}}\right)\\
&=\sqrt{4\pi}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\mb{j}_{k’}(t)\cdot\mb{a}_k(t)\int d^{3}\mb{r}\,e^{i(\mb{k}’+\mb{k})\cdot\mb{r}}\\
&=\sqrt{4\pi}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\mb{j}_{k’}(t)\cdot\mb{a}_k(t)\,(2\pi)^{3}\delta^{3}(\mb{k}’+\mb{k})\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\sqrt{4\pi}\,\mb{j}_{-k}(t)\cdot\mb{a}_k(t),\\
\therefore\quad S_2&=-\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\rho_{-k}(t)\,\phi_k(t)
-\sqrt{4\pi}\,\mb{j}_{-k}(t)\cdot\mb{a}_k(t)\,\right\}
\tag{7}
\end{align}
S_2&=-\int dt\int d^{3}\mb{r}\,\left[\rho(\mb{r},t)\phi(\mb{r},t)-\reverse{c}\mb{j}(\mb{r},t)\cdot
\mb{A}(\mb{r},t)\right],\\
\int d^{3}\mb{r}\,\rho\,\phi&=\int d^{3}\mb{r}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,\rho_{k’}(t)\,e^{i\mb{k}’\cdot\mb{r}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_k(t)
\,e^{i\mb{k}\cdot\mb{r}}\\
&=\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{k’}(t)\,
\phi_k(t)\int d^{3}\mb{r}\,e^{i(\mb{k}’+\mb{k})\cdot\mb{r}}\\
&=\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{k’}(t)\,
\phi_k(t)\,(2\pi)^{3}\delta^{3}(\mb{k}’+\mb{k})\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_{-k}(t)\,\phi_k(t),\\
\reverse{c}\int d^{3}\mb{r}\,\mb{j}\cdot\mb{A}&=\reverse{c}\int d^{3}\mb{r}\,\left(\int
\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\,\mb{j}_{k’}(t)\,e^{i\mb{k}’\cdot\mb{r}}\right)\cdot
\left(\sqrt{4\pi}c\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\mb{a}_k(t)\,e^{i\mb{k}\cdot\mb{r}}\right)\\
&=\sqrt{4\pi}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\mb{j}_{k’}(t)\cdot\mb{a}_k(t)\int d^{3}\mb{r}\,e^{i(\mb{k}’+\mb{k})\cdot\mb{r}}\\
&=\sqrt{4\pi}\int\frac{d^{3}\mb{k}’}{(2\pi)^{3}}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\mb{j}_{k’}(t)\cdot\mb{a}_k(t)\,(2\pi)^{3}\delta^{3}(\mb{k}’+\mb{k})\\
&=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\sqrt{4\pi}\,\mb{j}_{-k}(t)\cdot\mb{a}_k(t),\\
\therefore\quad S_2&=-\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\rho_{-k}(t)\,\phi_k(t)
-\sqrt{4\pi}\,\mb{j}_{-k}(t)\cdot\mb{a}_k(t)\,\right\}
\tag{7}
\end{align}
次に \(S_2\) と \(S_3\) から \(\phi_k\) の項のみを集めて \(S_c\) とすると,
\begin{equation}
S_c=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\reverse{2}\frac{k^{2}}{4\pi}\phi_k^{*}(t)\,\phi_k(t)
-\rho_{-k}(t)\,\phi_k(t)\,\right\}
\tag{8}
\end{equation}
S_c=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\reverse{2}\frac{k^{2}}{4\pi}\phi_k^{*}(t)\,\phi_k(t)
-\rho_{-k}(t)\,\phi_k(t)\,\right\}
\tag{8}
\end{equation}
ここで, 式 (9-14) の \(\phi(\mb{r},t)\) 及び \(\rho(\mb{r},t)\) の複素共役をとってみると,
\begin{equation}
\phi^{*}(\mb{r},t)=\int_{-\infty}^{\infty}\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_k^{*}\,e^{-i\mb{k}\cdot\mb{r}},
\quad
\rho^{*}(\mb{r},t)=\int_{-\infty}^{\infty}\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_k^{*}\,e^{-i\mb{k}\cdot\mb{r}}
\end{equation}
\phi^{*}(\mb{r},t)=\int_{-\infty}^{\infty}\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_k^{*}\,e^{-i\mb{k}\cdot\mb{r}},
\quad
\rho^{*}(\mb{r},t)=\int_{-\infty}^{\infty}\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\rho_k^{*}\,e^{-i\mb{k}\cdot\mb{r}}
\end{equation}
このとき \(\mb{k}\to-\mb{k}\) の変数変換を行ってみると, 例えば \(\phi\) の場合では次となる：
\begin{equation}
\phi^{*}(\mb{r},t)=\int_{-\infty}^{\infty}\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_{-k}^{*}
\,e^{i\mb{k}\cdot\mb{r}},\quad\left[\,\text{(cf.)}\quad
\phi(\mb{r},t)=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_{k}\,e^{i\mb{k}\cdot\mb{r}}\,\right]
\end{equation}
\phi^{*}(\mb{r},t)=\int_{-\infty}^{\infty}\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_{-k}^{*}
\,e^{i\mb{k}\cdot\mb{r}},\quad\left[\,\text{(cf.)}\quad
\phi(\mb{r},t)=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\phi_{k}\,e^{i\mb{k}\cdot\mb{r}}\,\right]
\end{equation}
これを式 (9-14) の \(\phi\) と比較すると \(\phi_k^{*}=\phi_{-k}\) が成り立つことが分かる．また同様なことが \(\rho\) についても成り立つから, 式 (9-17) の複素共役も含めて次が言える：
\begin{align}
&\phi_{-k}^{*}(t)=\phi_k(t),\quad\text{or}\quad \phi_k^{*}(t)=\phi_{-k}(t),\quad\text{where}\quad
\phi_{k}=\frac{4\pi}{k^{2}}\rho_k(t)\\
&\rho_{-k}^{*}(t)=\rho_k(t),\quad\text{or}\quad \rho_k^{*}(t)=\rho_{-k}(t),\\
\rightarrow\quad &\phi_k^{*}(t)=\frac{4\pi}{k^{2}}\rho_k^{*}(t)=\frac{4\pi}{k^{2}}\rho_{-k}(t)=\phi_{-k}(t)
\quad\therefore\quad \phi_k^{*}(t)=\frac{4\pi}{k^{2}}\rho_{-k}(t)
\tag{9}
\end{align}
&\phi_{-k}^{*}(t)=\phi_k(t),\quad\text{or}\quad \phi_k^{*}(t)=\phi_{-k}(t),\quad\text{where}\quad
\phi_{k}=\frac{4\pi}{k^{2}}\rho_k(t)\\
&\rho_{-k}^{*}(t)=\rho_k(t),\quad\text{or}\quad \rho_k^{*}(t)=\rho_{-k}(t),\\
\rightarrow\quad &\phi_k^{*}(t)=\frac{4\pi}{k^{2}}\rho_k^{*}(t)=\frac{4\pi}{k^{2}}\rho_{-k}(t)=\phi_{-k}(t)
\quad\therefore\quad \phi_k^{*}(t)=\frac{4\pi}{k^{2}}\rho_{-k}(t)
\tag{9}
\end{align}
従って, 式 (9-17) とこの式 (9) を式 (8) に代入すると,
\begin{align}
S_c&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\reverse{2}\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k
-\rho_{-k}(t)\,\phi_k(t)\,\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\reverse{2}\frac{k^{2}}{4\pi}
\frac{4\pi}{k^{2}}\rho_{-k}(t)\,\frac{4\pi}{k^{2}}\rho_k(t)
-\rho_{-k}(t)\,\frac{4\pi}{k^{2}}\rho_k(t)\,\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{\reverse{2}\frac{4\pi}{k^{2}}\rho_{-k}(t)\,\rho_k(t)
-\frac{4\pi}{k^{2}}\rho_{-k}(t)\rho_k(t)\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}
\rho_k(t)\rho_{-k}(t)\,\right\}
\tag{10}
\end{align}
S_c&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\reverse{2}\frac{k^{2}}{4\pi}\phi_k^{*}\,\phi_k
-\rho_{-k}(t)\,\phi_k(t)\,\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\left\{\,\reverse{2}\frac{k^{2}}{4\pi}
\frac{4\pi}{k^{2}}\rho_{-k}(t)\,\frac{4\pi}{k^{2}}\rho_k(t)
-\rho_{-k}(t)\,\frac{4\pi}{k^{2}}\rho_k(t)\,\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{\reverse{2}\frac{4\pi}{k^{2}}\rho_{-k}(t)\,\rho_k(t)
-\frac{4\pi}{k^{2}}\rho_{-k}(t)\rho_k(t)\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}
\rho_k(t)\rho_{-k}(t)\,\right\}
\tag{10}
\end{align}
更に, 式 (9-16) から次が言える：
\begin{equation}
\rho_k(t)=\sum_j e_j\,e^{-i\mb{k}\cdot\mb{q}_j(t)},\quad\rightarrow\quad
\rho_{-k}(t)=\sum_i e_i\,e^{i\mb{k}\cdot\mb{q}_i(t)}
\tag{11}
\end{equation}
\rho_k(t)=\sum_j e_j\,e^{-i\mb{k}\cdot\mb{q}_j(t)},\quad\rightarrow\quad
\rho_{-k}(t)=\sum_i e_i\,e^{i\mb{k}\cdot\mb{q}_i(t)}
\tag{11}
\end{equation}
これを上の式 (10) に代入すると,
\begin{align}
S_c&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}\rho_k(t)\rho_{-k}(t)\,\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}
\sum_j e_j\,e^{-i\mb{k}\cdot\mb{q}_j(t)}\sum_i e_i\,e^{i\mb{k}\cdot\mb{q}_i(t)}\,\right\}\\
&=\int dt\,\sum_i\sum_j e_i\,e_j\,\left\{-\reverse{2}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\frac{4\pi}{k^{2}}e^{i\mb{k}\cdot(\mb{q}_i-\mb{q}_j)}\right\}
\tag{12}
\end{align}
S_c&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}\rho_k(t)\rho_{-k}(t)\,\right\}\\
&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}
\sum_j e_j\,e^{-i\mb{k}\cdot\mb{q}_j(t)}\sum_i e_i\,e^{i\mb{k}\cdot\mb{q}_i(t)}\,\right\}\\
&=\int dt\,\sum_i\sum_j e_i\,e_j\,\left\{-\reverse{2}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\frac{4\pi}{k^{2}}e^{i\mb{k}\cdot(\mb{q}_i-\mb{q}_j)}\right\}
\tag{12}
\end{align}
このとき, 問題 9-3 で求めた式 (8) 及び式 (9) から, グリーン関数 \(G(\mb{x})\) について次が言える：
\begin{equation}
G(\mb{x})=\reverse{4\pi|\mb{x}|}=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\frac{e^{i\mb{k}\cdot\mb{r}}}{k^{2}}
\quad\rightarrow\quad \int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\frac{4\pi}{k^{2}}\,e^{i\mb{k}\cdot\mb{r}}
=\reverse{|\mb{x}|}
\tag{13}
\end{equation}
G(\mb{x})=\reverse{4\pi|\mb{x}|}=\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\frac{e^{i\mb{k}\cdot\mb{r}}}{k^{2}}
\quad\rightarrow\quad \int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\frac{4\pi}{k^{2}}\,e^{i\mb{k}\cdot\mb{r}}
=\reverse{|\mb{x}|}
\tag{13}
\end{equation}
これを上式 (12) に用いるならば,
\begin{align}
S_c&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}\rho_k(t)\rho_{-k}(t)
\,\right\}=\int dt\,\sum_i\sum_j e_i\,e_j\,\left\{-\reverse{2}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\frac{4\pi}{k^{2}}e^{i\mb{k}\cdot(\mb{q}_i-\mb{q}_j)}\right\}\\
&=\int dt\,\sum_i\sum_j e_i\,e_j\,\left\{-\reverse{2}\reverse{|\mb{q}_i-\mb{q}_j|}\right\}
=-\reverse{2}\int dt\,\left[\,\sum_i\sum_j \frac{e_i\,e_j}{|\mb{q}_i-\mb{q}_j|}\,\right]
\tag{14}
\end{align}
S_c&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left\{-\reverse{2}\frac{4\pi}{k^{2}}\rho_k(t)\rho_{-k}(t)
\,\right\}=\int dt\,\sum_i\sum_j e_i\,e_j\,\left\{-\reverse{2}\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,
\frac{4\pi}{k^{2}}e^{i\mb{k}\cdot(\mb{q}_i-\mb{q}_j)}\right\}\\
&=\int dt\,\sum_i\sum_j e_i\,e_j\,\left\{-\reverse{2}\reverse{|\mb{q}_i-\mb{q}_j|}\right\}
=-\reverse{2}\int dt\,\left[\,\sum_i\sum_j \frac{e_i\,e_j}{|\mb{q}_i-\mb{q}_j|}\,\right]
\tag{14}
\end{align}
すなわち, 我々はこのクーロン相互作用 \(S_c\) を「物質(matter) の作用 \(S_{mat}\)」 の中に含めることにする：
\begin{equation}
S_{mat}=S_1+S_c=\int dt\,\sum_i\left(\frac{m_i}{2}\dot{q}_i^{2}-\reverse{2}\sum_j\frac{e_i\,e_j}{|\mb{q}_i
-\mb{q}_j|}\right)
\tag{9-30}
\end{equation}
S_{mat}=S_1+S_c=\int dt\,\sum_i\left(\frac{m_i}{2}\dot{q}_i^{2}-\reverse{2}\sum_j\frac{e_i\,e_j}{|\mb{q}_i
-\mb{q}_j|}\right)
\tag{9-30}
\end{equation}
そして, 全体の作用を \(S=S_{mat}+S_{int}+S_{rad}\) と書き表わすことにする．従って, 電磁場の作用 \(S_3\) を2つの部分に分けた訳である：\(S_2+S_3=S_c+S_{rad}+S_{int}\)． 従って, \[ S=S_1+S_2+S_3=S_1+S_c+S_{rad}+S_{int}=S_{mat}+S_{rad}+S_{int}\]
「\(S_c\) は瞬間的なクーロン相互作用」に寄与する．そして残りは「輻射場：\(S_{rad}\)」と呼ぶことにする．(輻射場は瞬間場に対する補正を表わす．例えば, 全体の効果は遅れを伴うものであり, 光の速さを超えて作用することはないからである)．
「輻射場の作用」 \(S_{rad}\) は, \(S_3\) から \(\phi_k\) を含む項を差し引いたものである．すなわち,
\begin{align}
S_{rad}&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k
-k^{2}c^{2}\mb{a}_k^{*}\cdot\mb{a}_k\right)\notag\\
&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(\dot{a}_{1\mb{k}}^{*}\,
\dot{a}_{1\mb{k}}-k^{2}c^{2}a_{1\mb{k}}^{*}a_{1\,\mb{k}}+\dot{a}_{2\mb{k}}^{*}\dot{a}_{2\mb{k}}
-k^{2}c^{2}a_{2\mb{k}}^{*}a_{2\mb{k}}\Bigr)
\tag{9-31}
\end{align}
S_{rad}&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\left(\dot{\mb{a}}_k^{*}\cdot\dot{\mb{a}}_k
-k^{2}c^{2}\mb{a}_k^{*}\cdot\mb{a}_k\right)\notag\\
&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(\dot{a}_{1\mb{k}}^{*}\,
\dot{a}_{1\mb{k}}-k^{2}c^{2}a_{1\mb{k}}^{*}a_{1\,\mb{k}}+\dot{a}_{2\mb{k}}^{*}\dot{a}_{2\mb{k}}
-k^{2}c^{2}a_{2\mb{k}}^{*}a_{2\mb{k}}\Bigr)
\tag{9-31}
\end{align}
この \(S_{rad}\) は, まさに「輻射振動子の作用」である！．
「輻射振動子と粒子の相互作用」の作用積分 \(S_{int}\) は, 式(9-28)の \(S_2\) から \(\phi_k\) の含まれる項を除いたものである．従って次となる：
\begin{equation}
S_{int}=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sqrt{4\pi}\mb{j}_{-k}\cdot\mb{a}_k
=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(j_{1,-\mb{k}}\,a_{1\mb{k}}+j_{2,-\mb{k}}\,
a_{2\mb{k}}\Bigr)
\tag{9-32}
\end{equation}
S_{int}=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sqrt{4\pi}\mb{j}_{-k}\cdot\mb{a}_k
=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(j_{1,-\mb{k}}\,a_{1\mb{k}}+j_{2,-\mb{k}}\,
a_{2\mb{k}}\Bigr)
\tag{9-32}
\end{equation}
\(a_{1\mb{k}}\) と \(a_{2\mb{k}}\) について全作用 \(S\) を変分すると, 運動方程式 (9-21) と式 (9-22) が得られることは明らかである．[2]\(S=S_{mat}+S_{int}+S_{rad}\) の \(a_{1\mb{k}}\) と \(a_{2\mb{k}}\) の変分に関係するのは, 明らかに \(S_{rad}\) と \(S_{int}\) だけである.問題 9-4 … Continue reading
式 (9-16) から \(\mb{j}_{-k}=\sum_j e_j\dot{\mb{q}}_j(t)\,e^{i\mb{k}\cdot\mb{q}_j(t)}\) である．これを式 (9-32) の作用 \(S_{int}\) に代入して, より明示的に書き表わそう． \(\mb{a}\) と \(\mb{q}_j\) を (縦成分, 横成分) の成分表示をするならば, \(\mb{a}_k=(0,a_{1\mb{k}},a_{2\mb{k}})\) 及び \(\dot{\mb{q}}_j=(\dot{q}_{kj},\dot{q}_{1j},\dot{q}_{2j})\) となるので, \(\dot{\mb{q}}_j(t)\cdot\mb{a}_k=\dot{q}_{1j}a_{1k}+\dot{q}_{2j}a_{2k}\) である．よって作用 \(S_{int}\) は次となる：
\begin{align}
S_{int}&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sqrt{4\pi}\mb{j}_{-k}\cdot\mb{a}_k
=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_j e_j\,\dot{\mb{q}}_j(t)\cdot\mb{a}_k
\,e^{i\mb{k}\cdot\mb{q}_j(t)}\notag\\
&=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_j e_j\Bigl(a_{1\mb{k}}\dot{q}_{1j}+
a_{2\mb{k}}\dot{q}_{2j}\Bigr)\,e^{i\mb{k}\cdot\mb{q}_j(t)}
\tag{9-33}
\end{align}
S_{int}&=\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sqrt{4\pi}\mb{j}_{-k}\cdot\mb{a}_k
=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_j e_j\,\dot{\mb{q}}_j(t)\cdot\mb{a}_k
\,e^{i\mb{k}\cdot\mb{q}_j(t)}\notag\\
&=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_j e_j\Bigl(a_{1\mb{k}}\dot{q}_{1j}+
a_{2\mb{k}}\dot{q}_{2j}\Bigr)\,e^{i\mb{k}\cdot\mb{q}_j(t)}
\tag{9-33}
\end{align}
ただし \(q_{1j}\) と \(q_{2j}\) は \(\mb{k}\) に垂直な方向への \(\mb{q}_j\) の成分である．よって, 非相対論的力学と電気力学の全ての法則は, 次の命題(proposition)
にまとめられる．すなわち,「式 (9-30), 式 (9-31), 式 (9-33) の和である作用 \(S\) は, 変数 \(\mb{q}_j(t),a_{1\mb{k}}(t),a_{2\mb{k}}(t)\) の経路の変分に対して停留値をとる」：
\[\delta S=0,\quad S=S_{mat}+S_{rad}+S_{int}\]
ただし,
\begin{align}
S_{mat}&=\int dt\,\sum_i\left(\frac{m_i}{2}\dot{q}_i^{2}-\reverse{2}\sum_j\frac{e_i\,e_j}{|\mb{q}_i-\mb{q}_j|}\right)\\
S_{rad}&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(\dot{a}_{1\mb{k}}^{*}\,
\dot{a}_{1\mb{k}}-k^{2}c^{2}a_{1\mb{k}}^{*}a_{1\,\mb{k}}+\dot{a}_{2\mb{k}}^{*}\dot{a}_{2\mb{k}}
-k^{2}c^{2}a_{2\mb{k}}^{*}a_{2\mb{k}}\Bigr)\\
S_{int}&=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_j e_j\Bigl(a_{1\mb{k}}\dot{q}_{1j}+
a_{2\mb{k}}\dot{q}_{2j}\Bigr)\,e^{i\mb{k}\cdot\mb{q}_j(t)}
\end{align}
S_{mat}&=\int dt\,\sum_i\left(\frac{m_i}{2}\dot{q}_i^{2}-\reverse{2}\sum_j\frac{e_i\,e_j}{|\mb{q}_i-\mb{q}_j|}\right)\\
S_{rad}&=\reverse{2}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\Bigl(\dot{a}_{1\mb{k}}^{*}\,
\dot{a}_{1\mb{k}}-k^{2}c^{2}a_{1\mb{k}}^{*}a_{1\,\mb{k}}+\dot{a}_{2\mb{k}}^{*}\dot{a}_{2\mb{k}}
-k^{2}c^{2}a_{2\mb{k}}^{*}a_{2\mb{k}}\Bigr)\\
S_{int}&=\sqrt{4\pi}\int dt\int\frac{d^{3}\mb{k}}{(2\pi)^{3}}\,\sum_j e_j\Bigl(a_{1\mb{k}}\dot{q}_{1j}+
a_{2\mb{k}}\dot{q}_{2j}\Bigr)\,e^{i\mb{k}\cdot\mb{q}_j(t)}
\end{align}
「量子電気力学は, これらの経路について \(e^{iS/\hbar}\) を積分する結果として生じるものである」．それは次節で記述される．
References
| ↑1 | 式 (9-24) から式 (9-26) の作用積分はどのようにして得られたのかと疑問に思う必要はない．高橋康：「量子力学を学ぶための解析力学入門」に次のような文章があった：
|
|---|---|
| ↑2 | \(S=S_{mat}+S_{int}+S_{rad}\) の \(a_{1\mb{k}}\) と \(a_{2\mb{k}}\) の変分に関係するのは, 明らかに \(S_{rad}\) と \(S_{int}\) だけである.問題 9-4 で述べたオイラー=ラグランジュ方程式は, この場合には \(\mb{k}\) 空間に於ける式と考え, 変数 \(a_{1\mb{k}}\) 及び \(a_{2\mb{k}}\) を \(a_k\) と記すならば次とすればよいであろう： \begin{equation} \sum_{i}\pdiff{k_i}\left(\ppdiff{\mathscr{L}}{(\partial a_k/\partial k_i)}\right) +\pdiff{t}\ppdiff{\mathscr{L}}{(\partial a_k/\partial t)}-\ppdiff{\mathscr{L}}{a_k}=0 \tag{1} \end{equation} このとき関係するラグランジアン密度は次である： \begin{equation} \mathscr{L}=\mathscr{L}_{rad}+\mathscr{L}_{int},\quad \mathscr{L}_{rad}=\reverse{2}\dot{a}_k^{\,2}-\reverse{2} k^{2}c^{2}a_k^{\,2},\quad \mathscr{L}_{int}=\sqrt{4\pi}\,j_{-k}\,a_k \tag{2} \end{equation} 従って, 例えば \(a_{k}=a_{1\mb{k}}\) についてのオイラー=ラグランジュ方程式は次となる： \begin{align} \pdiff{k_x}\ppdiff{\mathscr{L}}{(\partial a_k/\partial k_x)}&+\pdiff{k_y} \ppdiff{\mathscr{L}}{(\partial a_k/\partial k_y)}+\pdiff{k_z} \ppdiff{\mathscr{L}}{(\partial a_k/\partial k_z)}+\pdiff{t}\ppdiff{\mathscr{L}}{\dot{a}_k} -\ppdiff{\mathscr{L}}{a_k}\\ &=\pdiff{t}\ppdiff{\mathscr{L}}{\dot{a}_k}-\ppdiff{\mathscr{L}}{a_k} =\pdiff{t}\reverse{2}2\dot{a}_k+\reverse{2}k^{2}c^{2}\,2a_k-\sqrt{4\pi}\,j_{-k}=0\\ \therefore\quad &\ddot{a}_{1\mb{k}}+k^{2}c^{2}\,a_{1\mb{k}}=\sqrt{4\pi}j_{1,-\mb{k}} \end{align} だが, この結果はその右辺が式 (9-21) と一致していない！．しかしながら, 図１の右図を見れば分かるように, 偏極ベクトル \(\epsilon^{(1)}\) と \(\epsilon^{(2)}\) の位置関係は \((\epsilon^{(1)},\epsilon^{(2)},\mb{k})\) がこの順で右手系となるように選定するのであった．よって, 右図の \(-\mb{k}\) の場合は, 左図の位置関係と全く同じであることになる．従って, 右辺の量 \(\sqrt{4\pi}\,j_{1,-\mb{k}}\) は実質的に \(\sqrt{4\pi}\,j_{1\mb{k}}\) に等価だと考えて良いのであろう(?!)． |
