\(\)

Problem 6-20
Suppose \(V\) is turned on and off slowly. For example, let \(V(x,t)=V(x)f(t)\), where \(f(t)\) is smooth, as shown in Fig. 6-12.
\begin{equation}
\newcommand{\ds}[1]{\mbox{${\displaystyle\strut #1}$}}
\newcommand{\mb}[1]{\mathbf{#1}}
f(t)=\begin{cases} \ds{\frac{1}{2}e^{+\gamma t}} & \text{for}\quad t<0 \\
\ds{1-\frac{1}{2}e^{-\gamma t}} & \text{for}\quad \ds{0<t< \frac{T}{2}}\\
\ds{1-\frac{1}{2}e^{-\gamma (T-t)}} & \text{for}\quad \ds{\frac{T}{2}<t<T}\\
\ds{\frac{1}{2}e^{-\gamma (t-T)}} & \text{for}\quad t>T
\end{cases}
\tag{6-80}
\end{equation}
\newcommand{\ds}[1]{\mbox{${\displaystyle\strut #1}$}}
\newcommand{\mb}[1]{\mathbf{#1}}
f(t)=\begin{cases} \ds{\frac{1}{2}e^{+\gamma t}} & \text{for}\quad t<0 \\
\ds{1-\frac{1}{2}e^{-\gamma t}} & \text{for}\quad \ds{0<t< \frac{T}{2}}\\
\ds{1-\frac{1}{2}e^{-\gamma (T-t)}} & \text{for}\quad \ds{\frac{T}{2}<t<T}\\
\ds{\frac{1}{2}e^{-\gamma (t-T)}} & \text{for}\quad t>T
\end{cases}
\tag{6-80}
\end{equation}
The rise time of the function \(f(t)\) is \(1/\gamma\). Supposing that \(1/\gamma \ll T\), show that probability given by Eq. (6-79) is reduced by a factor \(\displaystyle{\left[\frac{\gamma^{2}}{\gamma^{2}+(E_m-E_n)^{2}/\hbar^{2}}\right]^{2}}\). In this definition of \(f(t)\) we will have a discontinuity in the second derivative with respect to time. Smoother functions make still further reductions.
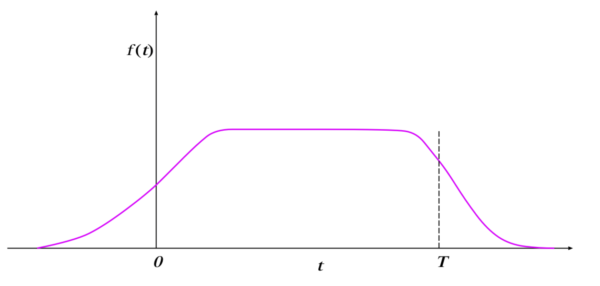
Fig. 6-12 The potential effecting the transition from \(n\) to \(m\) is turned on and off slowly with the time variation \(f(t)\), show here. As this time factor becomes smoother (e.g., as discontinuities appear in successively higher derivatives) the probability of a transition becomes smaller.
(解答) \(V(x,t)=V(x)f(t)\) とすると, 式 (6-71) より,
\begin{align}
V_{m n}(t)&=\int_{-\infty}^{\infty}dx\,\phi^{*}(x)V(x,t)\phi_n(x)=\int_{-\infty}^{\infty}dx\,\phi^{*}(x)V(x)f(t)\phi_n(x)
=f(t)\int_{-\infty}^{\infty}dx\,\phi^{*}(x)V(x)\phi_n(x)\notag\\
&=f(t)V_{mn}
\tag{1}
\end{align}
V_{m n}(t)&=\int_{-\infty}^{\infty}dx\,\phi^{*}(x)V(x,t)\phi_n(x)=\int_{-\infty}^{\infty}dx\,\phi^{*}(x)V(x)f(t)\phi_n(x)
=f(t)\int_{-\infty}^{\infty}dx\,\phi^{*}(x)V(x)\phi_n(x)\notag\\
&=f(t)V_{mn}
\tag{1}
\end{align}
従って式 (6-77) より, 式 (6-78) に相当するものは, \(\omega=(E_m-E_n)/\hbar\) として次となる:
\begin{align}
c_{m}^{(1)}&=\lambda_{mn}^{(1)}\,e^{i(E_m t_2-E_n t_1)/\hbar}
=-\frac{i}{\hbar}\int_{t_1}^{t_2} V_{m n}(t)\,e^{i(E_m-E_n)t/\hbar}\,dt\notag\\
&=-\frac{i}{\hbar}V_{mn}\int_{-\infty}^{\infty}dt\,f(t)\,e^{i\omega t}
\tag{2}
\end{align}
c_{m}^{(1)}&=\lambda_{mn}^{(1)}\,e^{i(E_m t_2-E_n t_1)/\hbar}
=-\frac{i}{\hbar}\int_{t_1}^{t_2} V_{m n}(t)\,e^{i(E_m-E_n)t/\hbar}\,dt\notag\\
&=-\frac{i}{\hbar}V_{mn}\int_{-\infty}^{\infty}dt\,f(t)\,e^{i\omega t}
\tag{2}
\end{align}
この積分部分の \(f(t)\) に式 (6-80) を代入したものを \(I=I_1+I_2+I_3+I_4\) としたとき, 各々の区間の積分は次となる:
\begin{align}
I_1&=\int_{-\infty}^{0}dt\,\frac{1}{2}e^{\gamma t}\,e^{i\omega t}=\frac{1}{2}\frac{1}{(\gamma+i\omega)},\notag\\
I_2&=\int_0^{T/2}dt\,\left(1-\frac{1}{2}e^{-\gamma t}\right)\,e^{i\omega t}
=\frac{e^{i\omega T/2}-1}{i\omega}+\frac{e^{-(\gamma-i\omega)T/2}-1}{2(\gamma-i\omega)},\notag\\
I_3&=\int_{T/2}^{T}dt\,\left(1-\frac{1}{2}e^{-\gamma(T-t)}\right)\,e^{i\omega t}
=\frac{e^{i\omega T}-e^{i\omega T/2}}{i\omega}+\frac{e^{-\gamma T/2}e^{i\omega T/2}
-e^{i\omega T}}{2(\gamma+i\omega)},\notag\\
I_4&=\int_{T}^{\infty}dt\,\frac{1}{2}e^{-\gamma(t-T)}\,e^{i\omega t}
=\frac{e^{i\omega T}}{2(\gamma-i\omega)}
\tag{3}
\end{align}
I_1&=\int_{-\infty}^{0}dt\,\frac{1}{2}e^{\gamma t}\,e^{i\omega t}=\frac{1}{2}\frac{1}{(\gamma+i\omega)},\notag\\
I_2&=\int_0^{T/2}dt\,\left(1-\frac{1}{2}e^{-\gamma t}\right)\,e^{i\omega t}
=\frac{e^{i\omega T/2}-1}{i\omega}+\frac{e^{-(\gamma-i\omega)T/2}-1}{2(\gamma-i\omega)},\notag\\
I_3&=\int_{T/2}^{T}dt\,\left(1-\frac{1}{2}e^{-\gamma(T-t)}\right)\,e^{i\omega t}
=\frac{e^{i\omega T}-e^{i\omega T/2}}{i\omega}+\frac{e^{-\gamma T/2}e^{i\omega T/2}
-e^{i\omega T}}{2(\gamma+i\omega)},\notag\\
I_4&=\int_{T}^{\infty}dt\,\frac{1}{2}e^{-\gamma(t-T)}\,e^{i\omega t}
=\frac{e^{i\omega T}}{2(\gamma-i\omega)}
\tag{3}
\end{align}
これらを足し合わせて整理すると次となる:
\begin{align}
I&=I_1+I_2+I_3+I_4\notag\\
&=(1-e^{i\omega T})\left\{\frac{\gamma-i\omega}{2(\gamma^{2}+\omega^{2})}
-\frac{\gamma+i\omega}{2(\gamma^{2}+\omega^{2})}+\frac{i}{\omega}\right\}
+\frac{1}{2}e^{-\gamma T/2}e^{i\omega T/2}\left\{\frac{\gamma-i\omega}{\gamma^{2}+\omega^{2}}
+\frac{\gamma+i\omega}{\gamma^{2}+\omega^{2}}\right\}\notag\\
&=(1-e^{i\omega T})\frac{i\gamma^{2}}{\omega(\gamma^{2}+\omega^{2})}
+e^{-\gamma T/2}e^{i\omega T/2}\frac{\gamma}{\gamma^{2}+\omega^{2}}\notag\\
&\simeq \frac{\gamma^{2}}{(\gamma^{2}+\omega^{2})}\frac{e^{i\omega T}-1}{i\omega}
\tag{4}
\end{align}
I&=I_1+I_2+I_3+I_4\notag\\
&=(1-e^{i\omega T})\left\{\frac{\gamma-i\omega}{2(\gamma^{2}+\omega^{2})}
-\frac{\gamma+i\omega}{2(\gamma^{2}+\omega^{2})}+\frac{i}{\omega}\right\}
+\frac{1}{2}e^{-\gamma T/2}e^{i\omega T/2}\left\{\frac{\gamma-i\omega}{\gamma^{2}+\omega^{2}}
+\frac{\gamma+i\omega}{\gamma^{2}+\omega^{2}}\right\}\notag\\
&=(1-e^{i\omega T})\frac{i\gamma^{2}}{\omega(\gamma^{2}+\omega^{2})}
+e^{-\gamma T/2}e^{i\omega T/2}\frac{\gamma}{\gamma^{2}+\omega^{2}}\notag\\
&\simeq \frac{\gamma^{2}}{(\gamma^{2}+\omega^{2})}\frac{e^{i\omega T}-1}{i\omega}
\tag{4}
\end{align}
ただし, \(\gamma T\gg 1\) より \(e^{-\gamma T/2}\approx 0\) として第2項を無視する近似を行っている. 式 (2) に, この結果を代入すると,
\begin{equation}
c_{m}^{(1)}=\lambda_{mn}^{(1)}\,e^{i(E_m t_2-E_n t_1)/\hbar}=-\frac{i}{\hbar}V_{mn}
\frac{\gamma^{2}}{\gamma^{2}+\omega^{2}}\frac{e^{i\omega T}-1}{i\omega}
=\frac{\gamma^{2}}{\gamma^{2}+\omega^{2}}\,V_{mn}\,\frac{1-e^{i\omega T}}{\hbar\omega}
\tag{5}
\end{equation}
c_{m}^{(1)}=\lambda_{mn}^{(1)}\,e^{i(E_m t_2-E_n t_1)/\hbar}=-\frac{i}{\hbar}V_{mn}
\frac{\gamma^{2}}{\gamma^{2}+\omega^{2}}\frac{e^{i\omega T}-1}{i\omega}
=\frac{\gamma^{2}}{\gamma^{2}+\omega^{2}}\,V_{mn}\,\frac{1-e^{i\omega T}}{\hbar\omega}
\tag{5}
\end{equation}
この結果は, 式 (6-78) に因子 \(\displaystyle{\frac{\gamma^{2}}{\gamma^{2}+\omega^{2}}}\) だけが付加したものになっている.
また, 「遷移確率」は 遷移振幅 \(c_m^{(1)}\) を2乗したものである. よってそれは, 式 (6-79) に因子 \(\{\gamma^{2}/(\gamma^{2}+\omega^{2})\}^{2}\) を掛けたものとなる:
\begin{equation}
P(n\!\to\! m)=\left|c_m^{(1)}\right|^{2}=\left|\lambda_{mn}^{(1)}\right|^{2}
=\left(\frac{\gamma^{2}}{\gamma^{2}+\omega^{2}}\right)^{2}\times|V_{mn}|^{2}
\frac{4\sin^{2}(\omega T/2)}{(\hbar\omega)^{2}}
\tag{6}
\end{equation}
P(n\!\to\! m)=\left|c_m^{(1)}\right|^{2}=\left|\lambda_{mn}^{(1)}\right|^{2}
=\left(\frac{\gamma^{2}}{\gamma^{2}+\omega^{2}}\right)^{2}\times|V_{mn}|^{2}
\frac{4\sin^{2}(\omega T/2)}{(\hbar\omega)^{2}}
\tag{6}
\end{equation}
ただし, \(\omega=(E_m-E_n)/\hbar\) である.

