\(\)
Problem 9-9
For a complicated system moving nonrelativistically
\begin{equation}
\def\mb#1{\mathbf{#1}}
(j_{1\mb{k}})_{NM}=\sum_b \big(e_b\,\mb{e}_{1}\cdot\dot{\mb{q}}_b\,e^{-i\mb{k}\cdot\mb{q}_b}\big)_{NM}
\tag{9-56}
\end{equation}
\def\mb#1{\mathbf{#1}}
(j_{1\mb{k}})_{NM}=\sum_b \big(e_b\,\mb{e}_{1}\cdot\dot{\mb{q}}_b\,e^{-i\mb{k}\cdot\mb{q}_b}\big)_{NM}
\tag{9-56}
\end{equation}
where \(\mb{e}_1\) is a unit vector in the direction of the polarization of the light and \(e_b\) and \(\mb{q}_b\) are the charge and position of the \(b\)th particle. Assume the wavelength of the light is very large compared with the size of the atom, i.e., that the absolute square of the wave function describing the position of the \(b\)th electron falls to \(0\) over a distance small compared with \(1/k\). Show that we can then approximate \(e^{i\mb{k}\cdot\mb{q}_b}\) by unity and write the matrix element as
\begin{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
(j_{1\mb{k}})_{NM} = i\omega\,\mb{e}\cdot\mb{\mu}_{NM}
\tag{9-57}
\end{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
(j_{1\mb{k}})_{NM} = i\omega\,\mb{e}\cdot\mb{\mu}_{NM}
\tag{9-57}
\end{equation}
where
\begin{equation}
\mb{\mu}_{NM}=\sum_i (e_i\,\mb{q}_i)_{NM}
\tag{9-58}
\end{equation}
\mb{\mu}_{NM}=\sum_i (e_i\,\mb{q}_i)_{NM}
\tag{9-58}
\end{equation}
The function \(\mb{\mu}_{NM}\) is called the matrix element of the electric dipole moment of the atom, and the approximation used to derive Eq. (9-57) is called the dipole approximation. Show that the total probability to emit light in any direction per unit time is
\begin{equation}
\frac{dP}{dt}=\frac{4\omega^{3}}{3\hbar c^{3}}\,\big|\mb{\mu}_{NM}\big|^{2}
\tag{9-59}
\end{equation}
\frac{dP}{dt}=\frac{4\omega^{3}}{3\hbar c^{3}}\,\big|\mb{\mu}_{NM}\big|^{2}
\tag{9-59}
\end{equation}
(Integrate Eq. (9-54) over all directions, remembering that \(\mb{e}\) is perpendicular to \(\mb{k}\) and that there are two possible directions of polarization.)
( 解答 ) まず, 電流密度の展開係数 \(j_{\mb{k}}\) は, 式 (9-16) から
\begin{equation}
\mb{j}_{\mb{k}}=\sum_i e_i\,\dot{\mb{q}}_i(t)\,e^{-i\mb{k}\cdot\mb{q}_i(t)}\quad\rightarrow\quad
j_{1\mb{k}}=\sum_i e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i(t)\,e^{-i\mb{k}\cdot\mb{q}_i(t)}
\end{equation}
\mb{j}_{\mb{k}}=\sum_i e_i\,\dot{\mb{q}}_i(t)\,e^{-i\mb{k}\cdot\mb{q}_i(t)}\quad\rightarrow\quad
j_{1\mb{k}}=\sum_i e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i(t)\,e^{-i\mb{k}\cdot\mb{q}_i(t)}
\end{equation}
であった．従って, この系の場合の行列要素 \( (j_{1\mb{k}})_{NM}\) は式 (9-56) のようになる：
\begin{equation}
(j_{1\mb{k}})_{NM}=\int d^{3}\mb{q}\Psi^{*}_{N}j_{1\mb{k}}\Psi_{M} = \sum_i \Big(e_i \hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\,e^{-i\mb{k}\cdot\mb{q}_i}\Big)_{NM}
\end{equation}
(j_{1\mb{k}})_{NM}=\int d^{3}\mb{q}\Psi^{*}_{N}j_{1\mb{k}}\Psi_{M} = \sum_i \Big(e_i \hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\,e^{-i\mb{k}\cdot\mb{q}_i}\Big)_{NM}
\end{equation}
この問題は, ランダウ=リフシッツ：「力学・場の理論」( L-I とする), 「量子力学」( L-II とする), そしてJ.J.Sakurai：「Advanced Quantum Mechanics」( S-A とする)から関係する部分を抜粋して答えとすることにしよう．
( L-I の§ 76 より)：空間のある有限な体積中の自由な(つまり電荷のない状態での)電磁場を考える．便宜上それは長さ \(A,B,C\) の辺を持つ直方体の形をした十分に大きな体積であると仮定する．この直方体中で, 場を特徴付ける全ての量は3次元フーリエ級数に展開できる．例えば, ベクトルポテンシャル \(\mb{A}\) は, それが実数であることを明らかにした形に書かれる：
\begin{equation}
\mb{A}=\sum_{\mb{k}} \mathrm{Re}\Bigl\{\,\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\Bigr\}\quad\rightarrow\quad
\mb{A}=\sum_{\mb{k}} \Bigl\{\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}+\mb{a}^{\,*}_{\mb{k}}(t)
\,e^{-i\mb{k}\cdot\mb{r}}\Bigr\}
\tag{1}
\end{equation}
\mb{A}=\sum_{\mb{k}} \mathrm{Re}\Bigl\{\,\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\Bigr\}\quad\rightarrow\quad
\mb{A}=\sum_{\mb{k}} \Bigl\{\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}+\mb{a}^{\,*}_{\mb{k}}(t)
\,e^{-i\mb{k}\cdot\mb{r}}\Bigr\}
\tag{1}
\end{equation}
ベクトルポテンシャルは, 次の「横波の条件」(transversality condition) を満足しているもの, すなわち「放射ゲージ」(radiation gauge) を採用する．これは真空中( \(\rho=0\) , 従って \(\phi=0\) )に於ける「クーロンゲージ」(Coulomb gauge) を言う( S-A の§ 2-1)：
\begin{equation}
\phi=0,\quad \mathrm{and}\quad \mathrm{div}\,\mb{A}=0
\tag{2}
\end{equation}
\phi=0,\quad \mathrm{and}\quad \mathrm{div}\,\mb{A}=0
\tag{2}
\end{equation}
この方程式から, 各 \(\mb{k}\) に対して複素ベクトル \(\mb{a}_{\mb{k}}(t)\) が対応する波数ベクトル \(\mb{k}\) に直交することが導かれる：
\begin{align}
\nabla\cdot\mb{A}&=\sum_{\mb{k}}\mb{a}_{\mb{k}}(t)\cdot\nabla e^{i\mb{k}\cdot\mb{r}}+\sum_{\mb{k}}
\mb{a}^{\,*}_{\mb{k}}(t)\cdot\nabla e^{-i\mb{k}\cdot\mb{r}}
=\sum_{\mb{k}}i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,e^{i\mb{k}\cdot\mb{r}}+\sum_{\mb{k}}-i\mb{a}^{\,*}_{\mb{k}}(t)
\cdot\mb{k}\, e^{-i\mb{k}\cdot\mb{r}}\\
&=\sum_{\mb{k}} \left\{(i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,e^{i\mb{k}\cdot\mb{r}})+(i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,
e^{i\mb{k}\cdot\mb{r}})^{*}\right\}=0\quad\rightarrow\quad i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,e^{i\mb{k}\cdot\mb{r}}=0\\
&\qquad\qquad\therefore\quad \mb{a}_{\mb{k}}(t)\cdot\mb{k}=0
\end{align}
\nabla\cdot\mb{A}&=\sum_{\mb{k}}\mb{a}_{\mb{k}}(t)\cdot\nabla e^{i\mb{k}\cdot\mb{r}}+\sum_{\mb{k}}
\mb{a}^{\,*}_{\mb{k}}(t)\cdot\nabla e^{-i\mb{k}\cdot\mb{r}}
=\sum_{\mb{k}}i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,e^{i\mb{k}\cdot\mb{r}}+\sum_{\mb{k}}-i\mb{a}^{\,*}_{\mb{k}}(t)
\cdot\mb{k}\, e^{-i\mb{k}\cdot\mb{r}}\\
&=\sum_{\mb{k}} \left\{(i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,e^{i\mb{k}\cdot\mb{r}})+(i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,
e^{i\mb{k}\cdot\mb{r}})^{*}\right\}=0\quad\rightarrow\quad i\mb{a}_{\mb{k}}(t)\cdot\mb{k}\,e^{i\mb{k}\cdot\mb{r}}=0\\
&\qquad\qquad\therefore\quad \mb{a}_{\mb{k}}(t)\cdot\mb{k}=0
\end{align}
勿論ベクトル \(\mb{a}_{\mb{k}}(t)\) は時間の関数で, 次の方程式を満たす：[1]本文の式 (9-12) にあるように, \(\mb{A}\) は進行平面波で \(\mb{A}(\mb{r},t)=\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\) と仮定すると, 振幅 \(\mb{a}_{\mb{k}}\) … Continue reading
\begin{equation}
\ddot{\mb{a}}_{\mb{k}}(t)+k^{2}c^{2}\mb{a}_{\mb{k}}(t)=0
\tag{3}
\end{equation}
\ddot{\mb{a}}_{\mb{k}}(t)+k^{2}c^{2}\mb{a}_{\mb{k}}(t)=0
\tag{3}
\end{equation}
従って, ベクトル \(\mb{a}_{\mb{k}}(t)\) は振動数 \(\omega=kc\) を持つ単一周期を持つ関数になる．場の展開を, 進行平面波への分解となるような形に行うことにする．そのために, 各々の \(\mb{a}_{\mb{k}}(t)\) が時間的に \(e^{-i\omega t}\) という因子で依存するとしよう：
\begin{equation}
\mb{a}_{\mb{k}}(t)=\mb{a}_{\mb{k}}\, e^{-i\omega t},\quad \mb{a}_{\mb{k}}^{\,*}(t)=\mb{a}_{\mb{k}}^{\,*}e^{i\omega t}
\quad \omega=kc
\tag{4}
\end{equation}
\mb{a}_{\mb{k}}(t)=\mb{a}_{\mb{k}}\, e^{-i\omega t},\quad \mb{a}_{\mb{k}}^{\,*}(t)=\mb{a}_{\mb{k}}^{\,*}e^{i\omega t}
\quad \omega=kc
\tag{4}
\end{equation}
こうすると和(1)の各項は, 差 \((\mb{k}\cdot\mb{r}-\omega t)\) だけの関数となり, ベクトル \(\mb{k}\) の方向に伝播する波に対応するものとなるからである．また線形の演算だけをこれらの量に対して行なう限りにでは, 実数部分をとるという記号を落として, 複素数の量自体について演算を行なうことが出来る：
\begin{equation}
\mb{A}=\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
\tag{5}
\end{equation}
\mb{A}=\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
\tag{5}
\end{equation}
スカラーポテンシャル \(\phi=0\) のクーロンゲージを用いたときの, 真空中の電場 \(\mb{E}\) は式(5)から次となる：
\begin{equation}
\mb{E}=-\reverse{c}\ppdiff{\mb{A}}{t}-\mathrm{grad}\,\phi=-\reverse{c}\ppdiff{\mb{A}}{t}
=-\reverse{c}\times(-i\omega)\,\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}=\frac{i\omega}{c}\,\mb{A}
\tag{6}
\end{equation}
\mb{E}=-\reverse{c}\ppdiff{\mb{A}}{t}-\mathrm{grad}\,\phi=-\reverse{c}\ppdiff{\mb{A}}{t}
=-\reverse{c}\times(-i\omega)\,\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}=\frac{i\omega}{c}\,\mb{A}
\tag{6}
\end{equation}
この原子系中心位置 \(\mb{r}\) を原点とする座標系 \(\mb{q}\) で \(i\) 番目の電子位置を \(\mb{q}_i\) とすると, それは原子系の大きさ \(a\) の範囲内にあるべきだから \(\mb{q}_i\le \pm a\) である．よって, 位置 \(\mb{q}_i\) での電場 \(\mb{E}_i(\mb{q}_i)\) は式(6)を用いることで次のように表せよう：
\begin{align}
&\mb{E}(\mb{r})=\frac{i\omega}{c}\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}\equiv \mb{E}_0
\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}\ \rightarrow\quad
\mb{E}(\mb{q}_i)=\mb{E}_0\,\,e^{i(\mb{k}\cdot\mb{q}_i-\omega t)}\approx \exp(\pm ika)\,\mb{E}_0\,e^{-i\omega t}
\tag{7}
\end{align}
&\mb{E}(\mb{r})=\frac{i\omega}{c}\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}\equiv \mb{E}_0
\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}\ \rightarrow\quad
\mb{E}(\mb{q}_i)=\mb{E}_0\,\,e^{i(\mb{k}\cdot\mb{q}_i-\omega t)}\approx \exp(\pm ika)\,\mb{E}_0\,e^{-i\omega t}
\tag{7}
\end{align}
原子系に入射する輻射の電場(調和振動成分)の波長 \(\lambda=2\pi/k\) が原子系の大きさ\(a\) (原子内電子の波動関数の絶対値の2乗がその目安となる) に比べて大きく \(a\ll \lambda\) と仮定すると \(a\ll 2\pi/k\) すなわち \(ka\ll 1\) で微小量であるとして, 次のように展開近似することが出来るであろう：
\begin{equation}
\exp(i\mb{k}\cdot\mb{q}_i)\approx\exp(\pm ika)=1\pm ika +\reverse{2!}(\pm ika)^{2}+\dotsb, \qquad\therefore
\quad \exp(i\mb{k}\cdot\mb{q}_i)\approx 1
\tag{8}
\end{equation}
\exp(i\mb{k}\cdot\mb{q}_i)\approx\exp(\pm ika)=1\pm ika +\reverse{2!}(\pm ika)^{2}+\dotsb, \qquad\therefore
\quad \exp(i\mb{k}\cdot\mb{q}_i)\approx 1
\tag{8}
\end{equation}
よって, 原子内では電場の位置依存性は殆どなく \(\mb{E}(\mb{q}_i)=\mb{E}_0\,e^{-i\omega t}\) として良いと言える．
( L-II の§ 97 より)：光子の波長 \(\lambda\) が発光系(原子系)の大きさ \(a\) に較べて大きいときには上記のように \(\exp(i\mb{k}\cdot\mb{q}_i)\) を \(1\) で近似することが出来る．このような置き換えは「系に於いて, 粒子運動量に比べて光子運動量を無視することであり, この近似は輻射の古典論の双極輻射の場合に相当する」.
( L-II の§ 11 より)：まず物理量 \(f\) の行列についてまとめておく．便宜上, 考えている系は離散的エネルギースペクトルを持つと仮定する(以下で得られる全ての関数は連続的スペクトルの場合にも直ちに拡張出来る)．任意の波動関数 \(\varPsi(t)\) は, エネルギーの確定した定常状態の波動関数 \(\varPsi_n(t)\) によって展開することが出来るのであった：
\begin{equation}
\varPsi(t)=\sum_n c_n\varPsi_n(t),\quad \text{where}\quad \varPsi_n(t)=e^{-i\omega_n t}\phi_n(q)
\tag{9}
\end{equation}
\varPsi(t)=\sum_n c_n\varPsi_n(t),\quad \text{where}\quad \varPsi_n(t)=e^{-i\omega_n t}\phi_n(q)
\tag{9}
\end{equation}
また, 物理量演算子 \(\hat{f}\) の平均値 \(\bar{f}\) は次で定義された：
\begin{equation}
\bar{f}=\int \varPsi^{*}\left(\hat{f}\,\varPsi\right)\,dq=\int \varPsi^{*}\,\hat{f}\,\varPsi\,dq
\tag{10}
\end{equation}
\bar{f}=\int \varPsi^{*}\left(\hat{f}\,\varPsi\right)\,dq=\int \varPsi^{*}\,\hat{f}\,\varPsi\,dq
\tag{10}
\end{equation}
これに式(9)を代入すると次が得られる：
\begin{align}
\bar{f}&=\int \sum_n c_n^{*}\Psi^{*}_n(t)\hat{f}\sum_m c_m \Psi_m(t)
=\sum_n\sum_m c_n^{*}c_m\int \Psi^{*}_n(t)\hat{f}\,\Psi_m(t)\,dq
=\sum_n\sum_m c^{*}_nc_m\,f_{nm}(t),\\
&\quad \text{where}\quad f_{nm}(t)=\langle n|f|m\rangle=\int \varPsi^{*}_n\,\hat{f}\,\varPsi_m\,dq
\tag{11}
\end{align}
\bar{f}&=\int \sum_n c_n^{*}\Psi^{*}_n(t)\hat{f}\sum_m c_m \Psi_m(t)
=\sum_n\sum_m c_n^{*}c_m\int \Psi^{*}_n(t)\hat{f}\,\Psi_m(t)\,dq
=\sum_n\sum_m c^{*}_nc_m\,f_{nm}(t),\\
&\quad \text{where}\quad f_{nm}(t)=\langle n|f|m\rangle=\int \varPsi^{*}_n\,\hat{f}\,\varPsi_m\,dq
\tag{11}
\end{align}
このとき, 可能な全ての \(n,m\) をとる量 \(f_{nm}(t)\) の全体を, 量 \(f\) の「行列」と呼ぶ．また各 \(f_{nm}(t)\) を「状態 \(m\) から状態 \(n\) への遷移に対応する行列要素」と呼ぶ．
行列要素 \(f_{nm}(t)\) の時間依存性は, 演算子 \(\hat{f}\) が時間を顕に含まない場合には, 関数 \(\varPsi_n\) の時間依存性によって決められる．式(9)を式(11)に代入すれば, 次が得られる：
\begin{align}
f_{nm}(t)&=\int e^{+i\omega_n t}\phi_n(q)\hat{f}\,e^{-i\omega_m t}\phi_m(q)
=e^{i(\omega_n-\omega_m)t}\int \phi_n^{*}(q)\hat{f}\,\phi_m(q)\,dq \equiv f_{nm}\,e^{i\omega_{nm}t},\\
&\mathrm{where}\quad \omega_{nm}=\omega_n-\omega_m=\frac{E_n-E_m}{\hbar},\quad
f_{nm}=\int \phi_n^{*}(q)\,\hat{f}\,\phi_m(q)\,dq
\tag{12}
\end{align}
f_{nm}(t)&=\int e^{+i\omega_n t}\phi_n(q)\hat{f}\,e^{-i\omega_m t}\phi_m(q)
=e^{i(\omega_n-\omega_m)t}\int \phi_n^{*}(q)\hat{f}\,\phi_m(q)\,dq \equiv f_{nm}\,e^{i\omega_{nm}t},\\
&\mathrm{where}\quad \omega_{nm}=\omega_n-\omega_m=\frac{E_n-E_m}{\hbar},\quad
f_{nm}=\int \phi_n^{*}(q)\,\hat{f}\,\phi_m(q)\,dq
\tag{12}
\end{align}
このとき \(\omega_{nm}\) は状態 \(m\) と \(n\) の間のいわゆる「遷移振動数」であり, 量 \(f_{nm}\) は物理量 \(f\) の普通に用いられている時間に依存しない行列要素である．
この物理量 \(f\) が時間依存しない場合, 物理量 \(f\) の時間微分 \(\dot{f}\) の行列要素は,「導関数 \(\dot{f}\) の平均値 \(\overline{\dot{f}}\) は , 平均値 \(\overline{f}\) の導関数 \(\dot{\overline{f}}\) に一致すること」から直ちに得られる：
\begin{equation}
\overline{\dot{f}}=\dot{\overline{f}}=\frac{d}{dt}\int \Psi^{*}f\Psi\,dq
=\frac{d}{dt}\sum_{n,m}c_n^{*}c_m\,f_{nm}(t)=\sum_{n,m} c_n^{*}c_m\frac{d}{dt}f_{nm}(t)
\end{equation}
\overline{\dot{f}}=\dot{\overline{f}}=\frac{d}{dt}\int \Psi^{*}f\Psi\,dq
=\frac{d}{dt}\sum_{n,m}c_n^{*}c_m\,f_{nm}(t)=\sum_{n,m} c_n^{*}c_m\frac{d}{dt}f_{nm}(t)
\end{equation}
従って \(\dot{f}\) の行列要素 \((\dot{f})_{mn}(t)\) は, 形式的には単純に式(12)を時間微分して得られる：
\begin{align}
\frac{d}{dt} f_{nm}(t) &=\frac{d}{dt}\left(f_{nm}e^{i\omega_{nm}t}\right)
=f_{nm}\frac{d}{dt}e^{i\omega_{nm}t}
=i\omega_{nm}f_{nm}e^{i\omega_{nm}t}=i\omega_{nm}f_{nm}(t),\\
(\dot{f})_{nm}(t)&\equiv e^{i\omega_{nm}t}(\dot{f})_{nm},
\tag{13}
\end{align}
\frac{d}{dt} f_{nm}(t) &=\frac{d}{dt}\left(f_{nm}e^{i\omega_{nm}t}\right)
=f_{nm}\frac{d}{dt}e^{i\omega_{nm}t}
=i\omega_{nm}f_{nm}e^{i\omega_{nm}t}=i\omega_{nm}f_{nm}(t),\\
(\dot{f})_{nm}(t)&\equiv e^{i\omega_{nm}t}(\dot{f})_{nm},
\tag{13}
\end{align}
或いは, 両式から時間因子 \(e^{i\omega_{nm}t}\) を落とせば, 時間に依存しない行列要素 \((\dot{f})_{nm}\) が得られる：
\begin{align}
&(\dot{f})_{nm}(t)= e^{i\omega_{nm}t}(\dot{f})_{nm}=\frac{d}{dt} f_{nm}(t)
=i\omega_{nm}f_{nm}e^{i\omega_{nm}t},\\
\rightarrow &\quad (\dot{f})_{nm}=i\omega_{nm}\,f_{nm}=\frac{i}{\hbar}(E_n-E_m)\,f_{nm}
\tag{14}
\end{align}
&(\dot{f})_{nm}(t)= e^{i\omega_{nm}t}(\dot{f})_{nm}=\frac{d}{dt} f_{nm}(t)
=i\omega_{nm}f_{nm}e^{i\omega_{nm}t},\\
\rightarrow &\quad (\dot{f})_{nm}=i\omega_{nm}\,f_{nm}=\frac{i}{\hbar}(E_n-E_m)\,f_{nm}
\tag{14}
\end{align}
以上の結果式を, 具体的に \(f\) を位置ベクトル \(\mb{q}_i\) として考えて行く． \(\omega_{nm}=\omega\) と記すならば, 式(12)に相当する行列要素 \((\mb{q}_i)_{NM}\) と, 式(14)に相当する時間微分 \((\dot{\mb{q}}_i)_{NM}\) の時間依存しない行列要素は次になる：
\begin{align}
\left(\mb{q}_i\right)_{NM}(t)&=\left(\mb{q}_i\right)_{NM}\,e^{i\omega t},\quad\text{where}\quad
\left(\mb{q}_i\right)_{NM}=\int \psi_N^{*}(\mb{q})\,\mb{q}_i\,\psi_M(\mb{q})\,d^{3}\mb{q}
\tag{15}\\
&\left(\dot{\mb{q}}_i\right)_{NM}=i\omega_{NM}\left(\mb{q}_i\right)_{NM}
\tag{16}
\end{align}
\left(\mb{q}_i\right)_{NM}(t)&=\left(\mb{q}_i\right)_{NM}\,e^{i\omega t},\quad\text{where}\quad
\left(\mb{q}_i\right)_{NM}=\int \psi_N^{*}(\mb{q})\,\mb{q}_i\,\psi_M(\mb{q})\,d^{3}\mb{q}
\tag{15}\\
&\left(\dot{\mb{q}}_i\right)_{NM}=i\omega_{NM}\left(\mb{q}_i\right)_{NM}
\tag{16}
\end{align}
他方, 電気双極子モーメント \(\mb{\mu}\) の時間依存しない行列要素は次に書ける：
\begin{equation}
\mb{\mu}_{NM}=\sum_i \left(\mb{\mu}_i\right)_{NM}=\sum_i \left(e_i\mb{q}_i\right)_{NM}
\tag{17}
\end{equation}
\mb{\mu}_{NM}=\sum_i \left(\mb{\mu}_i\right)_{NM}=\sum_i \left(e_i\mb{q}_i\right)_{NM}
\tag{17}
\end{equation}
従って \(e^{i\mb{k}\cdot\mb{q}_i}\approx 1\) と近似した場合では, 偏極方向 \(1\) の光の「遷移電流密度」(transition current density)： \(\displaystyle{j_1=\sum_i e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i}\) のフーリエ変換 \(j_{1\mb{k}}\) に対する時間依存しない行列要素 \((j_{1\mb{k}})_{NM}\) は, 式(17)と式(16)から次に書ける：
\begin{align}
&j_{1\mb{k}}=\sum_i e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\,e^{-i\mb{k}\cdot\mb{q}_i}
\approx \sum_i e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\\
\rightarrow\quad \left(j_{1\mb{k}}\right)_{NM}&=\sum_i \left(e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\right)_{NM}
=\sum_i \hat{\mb{e}}_1\cdot\left(e_i\dot{\mb{q}}_i\right)_{NM}
=i\omega\,\hat{\mb{e}}_1\cdot\sum_i \left(e_i\mb{q}_i\right)_{NM}\\
&=i\omega\,\hat{\mb{e}}_1\cdot\mb{\mu}_{NM}
\tag{18}
\end{align}
&j_{1\mb{k}}=\sum_i e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\,e^{-i\mb{k}\cdot\mb{q}_i}
\approx \sum_i e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\\
\rightarrow\quad \left(j_{1\mb{k}}\right)_{NM}&=\sum_i \left(e_i\,\hat{\mb{e}}_1\cdot\dot{\mb{q}}_i\right)_{NM}
=\sum_i \hat{\mb{e}}_1\cdot\left(e_i\dot{\mb{q}}_i\right)_{NM}
=i\omega\,\hat{\mb{e}}_1\cdot\sum_i \left(e_i\mb{q}_i\right)_{NM}\\
&=i\omega\,\hat{\mb{e}}_1\cdot\mb{\mu}_{NM}
\tag{18}
\end{align}
この結果を本文の式 (9-54)：
\begin{equation*}
\frac{dP}{dt}=\frac{\omega}{2\pi\hbar c^{3}}\,\big|\bigl(j_{1\mb{k}}\bigr)_{NM}\big|^{2}\,d\Omega
\tag{9-54}
\end{equation*}
\frac{dP}{dt}=\frac{\omega}{2\pi\hbar c^{3}}\,\big|\bigl(j_{1\mb{k}}\bigr)_{NM}\big|^{2}\,d\Omega
\tag{9-54}
\end{equation*}
に代入し, 全ての方向について積分すると, 偏極方向 \(1\) の光についての単位時間に任意の方向に光が放出される全確率の式が得られる．
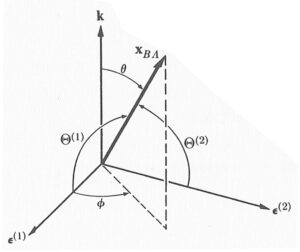
図 1. 電子の電気双極子モーメントを \(\mb{\mu}=e\mb{X}\) としたとき, その行列要素 \(\mb{\mu}_{BA}=e\mb{X}_{BA}\) と偏極ベクトル \(\mb{e}^{(i)}\) との位置関係を示す．光子の伝播方向は波数ベクトル \(\mb{k}\) の向きであり, 偏極ベクトル \(\mb{e}^{(1)},\mb{e}^{(2)}\) はそれに垂直な平面内に存在する． (J.J.Sakurai)
ただし, 各々の \(\mb{k}\) については2つの独立な偏極状態からの寄与がある．従ってそれらについて和をとり, 全ての可能な放射方向について積分を実行する．図 1 に示す通り, 角度の関係は次のように表される．
\begin{equation}
\cos\Theta^{(1)}=\sin\theta\cos\phi,\quad \cos\Theta^{(2)}=\sin\theta\sin\phi
\tag{19}
\end{equation}
\cos\Theta^{(1)}=\sin\theta\cos\phi,\quad \cos\Theta^{(2)}=\sin\theta\sin\phi
\tag{19}
\end{equation}
2つの偏極状態に関する和は, 単に \(\sin^{2}\theta\) という因子を与える：
\begin{equation}
\int \left\{\cos^{\,2}\Theta^{(1)}+\cos^{\,2}\Theta^{(2)}\right\}\,d\Omega
=\int \big\{\sin^{\,2}\theta\cos^{\,2}\phi+\sin^{\,2}\theta\sin^{\,2}\phi \big\}\,d\Omega
=\int \sin^{\,2}\theta\,d\Omega
\tag{20}
\end{equation}
\int \left\{\cos^{\,2}\Theta^{(1)}+\cos^{\,2}\Theta^{(2)}\right\}\,d\Omega
=\int \big\{\sin^{\,2}\theta\cos^{\,2}\phi+\sin^{\,2}\theta\sin^{\,2}\phi \big\}\,d\Omega
=\int \sin^{\,2}\theta\,d\Omega
\tag{20}
\end{equation}
空間内で \(\mb{\mu}_{NM}\) すなわち図の \(\mb{X}\) の方向を固定して考え, 全ての可能な放射方向に関する積分を考える．\(\cos\theta=x\) と置くと \(d(\cos\theta)=-\sin\theta\,d\theta=dx\) なので,
\begin{align}
\int_{\Omega} \sin^{\,2}\theta\,d\Omega&=\int \sin^{\,2}\theta\,\sin\theta\,d\theta d\phi
=\int_{0}^{2\pi}\,d\phi\int_{0}^{\pi}\sin^{\,2}\theta\sin\theta\,d\theta
=2\pi\int_{-1}^{1}\sin^{\,2}\theta\,d(\cos\theta)\\
&=2\pi\int_{-1}^{1}(1-x^{2})\,dx=\frac{8\pi}{3}
\tag{21}
\end{align}
\int_{\Omega} \sin^{\,2}\theta\,d\Omega&=\int \sin^{\,2}\theta\,\sin\theta\,d\theta d\phi
=\int_{0}^{2\pi}\,d\phi\int_{0}^{\pi}\sin^{\,2}\theta\sin\theta\,d\theta
=2\pi\int_{-1}^{1}\sin^{\,2}\theta\,d(\cos\theta)\\
&=2\pi\int_{-1}^{1}(1-x^{2})\,dx=\frac{8\pi}{3}
\tag{21}
\end{align}
以上を踏まえて, 次となる：
\begin{align}
\frac{d P}{d t}\biggl|_{\mathrm{whole}}
&=\frac{\omega}{2\pi\hbar c^{3}}\int \left\{\big|\bigl(j_{1\mb{k}}\bigr)_{NM}\big|^{2}_{NM}+\big|\bigl(j_{2\mb{k}}\bigr)_{NM}\big|^{2}\right\}\,d\Omega\\
&=\frac{\omega}{2\pi\hbar c^{3}}\int \left\{\Big|i\omega\,\hat{\mb{e}}_1\cdot\mb{\mu}_{NM}\Big|^{2}
+\Big|i\omega\,\hat{\mb{e}}_2\cdot\mb{\mu}_{NM}\Big|^{2}\right\}\,d\Omega\\
&=\frac{\omega}{2\pi\hbar c^{3}}\int \omega^{2}\big|\mb{\mu}_{NM}\big|^{2}\left\{
\cos^{\,2}\Theta^{(1)}+\cos^{\,2}\Theta^{(2)}\right\}\,d\Omega\\
&=\frac{\omega^{3}}{2\pi\hbar c^{3}}\Bigl|\mb{\mu}_{NM}\Bigr|^{2}\int \sin^{\,2}\theta\,d\Omega
=\frac{\omega^{3}}{2\pi\hbar c^{3}}\Bigl|\mb{\mu}_{NM}\Bigr|^{2}\times \frac{8\pi}{3}\\
&=\frac{4\omega^{3}}{3\hbar c^{3}}\left|\mb{\mu}_{NM}\right|^{2}
\tag{22}
\end{align}
\frac{d P}{d t}\biggl|_{\mathrm{whole}}
&=\frac{\omega}{2\pi\hbar c^{3}}\int \left\{\big|\bigl(j_{1\mb{k}}\bigr)_{NM}\big|^{2}_{NM}+\big|\bigl(j_{2\mb{k}}\bigr)_{NM}\big|^{2}\right\}\,d\Omega\\
&=\frac{\omega}{2\pi\hbar c^{3}}\int \left\{\Big|i\omega\,\hat{\mb{e}}_1\cdot\mb{\mu}_{NM}\Big|^{2}
+\Big|i\omega\,\hat{\mb{e}}_2\cdot\mb{\mu}_{NM}\Big|^{2}\right\}\,d\Omega\\
&=\frac{\omega}{2\pi\hbar c^{3}}\int \omega^{2}\big|\mb{\mu}_{NM}\big|^{2}\left\{
\cos^{\,2}\Theta^{(1)}+\cos^{\,2}\Theta^{(2)}\right\}\,d\Omega\\
&=\frac{\omega^{3}}{2\pi\hbar c^{3}}\Bigl|\mb{\mu}_{NM}\Bigr|^{2}\int \sin^{\,2}\theta\,d\Omega
=\frac{\omega^{3}}{2\pi\hbar c^{3}}\Bigl|\mb{\mu}_{NM}\Bigr|^{2}\times \frac{8\pi}{3}\\
&=\frac{4\omega^{3}}{3\hbar c^{3}}\left|\mb{\mu}_{NM}\right|^{2}
\tag{22}
\end{align}
References
| ↑1 | 本文の式 (9-12) にあるように, \(\mb{A}\) は進行平面波で \(\mb{A}(\mb{r},t)=\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\) と仮定すると, 振幅 \(\mb{a}_{\mb{k}}\) に対する方程式は次の様に求まる： \begin{align} \nabla^{2}\mb{A}=\frac{\partial^{2}}{\partial\mb{r}^{2}}\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}} &=\mb{a}_{\mb{k}}(t)\Bppdiff{e^{i\mb{k}\cdot\mb{r}}}{\mb{r}}=(i\mb{k})^{2}\mb{a}_{\mb{k}}(t)e^{i\mb{k} \cdot\mb{r}},\quad \Bppdiff{\mb{A}}{t}=\Bppdiff{\mb{a}_{\mb{k}}(t)}{t}\,e^{i\mb{k}\cdot\mb{r}} =\ddot{\mb{a}}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\\ \rightarrow\quad \nabla^{2}\mb{A}-\reverse{c^{2}}\Bppdiff{\mb{A}}{t}&=-{\mb{k}}^{2}\mb{a}_{\mb{k}}(t) e^{i\mb{k}\cdot\mb{r}}-\reverse{c^{2}}\ddot{\mb{a}}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}=0 \quad \rightarrow\quad k^{2}\mb{a}_{\mb{k}}(t)+\reverse{c^{2}}\ddot{\mb{a}}_{\mb{k}}(t)=0\\ \therefore\qquad &\ddot{\mb{a}}_{\mb{k}}(t)=-c^{2}k^{2}\,\mb{a}_{\mb{k}}(t) \end{align} これより \(\mb{a}_{\mb{k}}\) は, \(\mb{a}_k\) の各成分の方向について振動数 \(\omega=kc\) の単純な調和振動子であることが分かる．しかし実際には2つの独立な横波だけが存在する． |
|---|
