時間に依存するポテンシャル問題

問題 6-22 に答える準備として， J.J.Sakuri の § 5.5 の「時間に依存するポテンシャル：相互作用」の抜粋を示しておこう．

時間に依存するポテンシャル問題
時間に依存する２準位問題：核磁気共鳴やメーザーなど
1. スピン磁気共鳴
時間を含む摂動論

時間に依存するポテンシャル問題

系のハミルトニアンが二つの部分に分けられる場合を考える：

\begin{matrix} (1) & H = H_{0} + V (t), H_{0} | n ⟩ = E_{n} | n ⟩ \end{matrix}

ただし

H_{0}

は時間を露らわに含まない．始めに, すなわち

t = 0

で, 物理系の状態ケットは次で与えられると仮定する：

\begin{matrix} (2) & | α, t = 0 ⟩ = | α ⟩ = \sum_{n} c_{n} (0) | n ⟩ \end{matrix}

このとき, 時間

t > 0

のときの系の状態ケットを基礎ケットによって展開した時の展開係数

c_{n} (t)

を求めよう：

\begin{matrix} (3) & | α, t ⟩_{S} = \sum_{n} c_{n} (t) e^{- i E_{n} t / ℏ} | n ⟩ \end{matrix}

この式はシュレディンガー表示である．これを次のような「相互作用表示」で表現すると,

\begin{aligned} | α, t ⟩_{I} = e^{i H_{0} t / ℏ} | α, t ⟩_{S}, A_{I} = e^{i H_{0} t / ℏ} A_{S} e^{- i H_{0} t / ℏ}, \\ (4) & \to & H_{I} = e^{i H_{0} t / ℏ} {H_{0} + V (t)} e^{- i H_{0} t / ℏ} = H_{0} + e^{i H_{0} t / ℏ} V (t) e^{- i H_{0} t / ℏ} \end{aligned}

また, 相互作用表示の状態ケットの時間変化を定める基礎的な微分方程式はシュレディンガー方程式を用いて次となる：

\begin{aligned} i ℏ \frac{\partial}{\partial t} | α, t ⟩_{I} & = i ℏ \frac{\partial}{\partial t} (e^{i H_{0} t / ℏ} | α, t ⟩_{S}) \\ = i ℏ \cdot \frac{i H_{0}}{ℏ} e^{i H_{0} t / ℏ} | α, t ⟩_{S} + e^{i H_{0} t / ℏ} i ℏ \frac{\partial}{\partial t} | α, t ⟩_{S} \\ = - H_{0} | α, t ⟩_{I} + e^{i H_{0} t / ℏ} H | α, t ⟩_{S} \\ = - H_{0} | α, t ⟩_{I} + H_{0} e^{i H_{0} t / ℏ} | α, t ⟩_{S} + e^{i H_{0} t / ℏ} V (t) | α, t ⟩_{S} \\ = (e^{i H_{0} t / ℏ} V (t) e^{- i H_{0} t / ℏ}) (e^{i H_{0} t / ℏ} | α, t ⟩_{S}) \\ (5) & \to i ℏ \frac{\partial}{\partial t} | α, t ⟩_{I} & = V_{I} (t) | α, t ⟩_{I} \end{aligned}

また, 観測量

A

の時間変化を決定する基礎方程式は次となる：

\begin{matrix} (6) & i ℏ \frac{d A_{I}}{d t} = [A_{I}, H_{0}] \end{matrix}

これはハイゼンベルグ方程式と似ているが，

H

が

H_{0}

に置き換わっていることに注意する．
　次に上式(4)に式(3)を代入することで, 相互作用表示された状態ケット

| α, t ⟩_{I}

を基礎ケット

| n ⟩

で展開してみる：

\begin{aligned} | α, t ⟩_{I} & = e^{i H_{0} t / ℏ} | α, t ⟩_{S} = \sum_{n} c_{n} (t) e^{- i E_{n} t / ℏ} e^{i H_{0} t / ℏ} | n ⟩ \\ (7) & = \sum_{n} c_{n} (t) e^{- i E_{n} t / ℏ} e^{i E_{n} t / ℏ} | n ⟩ = \sum_{n} c_{n} (t) | n ⟩ \end{aligned}

これを式(5)に用いた後で, 両辺に左からブラ

⟨ m |

を掛け合わせると,

\begin{aligned} i ℏ \frac{\partial}{\partial t} ⟨ m | α, t ⟩_{I} & = i ℏ \frac{\partial}{\partial t} ⟨ n | (\sum_{n} c_{n} (t) | n ⟩) = i ℏ \frac{\partial}{\partial t} c_{m} (t) \\ = ⟨ m | V_{I} (t) (\sum_{n} c_{n} (t) | n ⟩) = \sum_{n} c_{n} (t) ⟨ m | V_{I} (t) | n ⟩ \\ = \sum_{n} c_{n} (t) ⟨ m | (e^{i H_{0} t / ℏ} V (t) e^{- i H_{0} t / ℏ}) | n ⟩ \\ = \sum_{n} c_{n} (t) ⟨ m | e^{i E_{m} t / ℏ} V (t) e^{- i E_{n} t / ℏ} | n ⟩ \\ (8) & = \sum_{n} c_{n} (t) e^{i (E_{m} - E_{n}) t / ℏ} ⟨ m | V (t) | n ⟩ \end{aligned}

従って次を得る：

\begin{matrix} (9) & i ℏ \frac{d}{d t} c_{m} (t) = \sum_{n} e^{i ω_{m n} t} V_{m n} (t) c_{n} (t), \end{matrix}

ただし

V_{m n} (t)

と

ω_{m n}

は次である：

\begin{matrix} (10) & V_{m n} (t) = ⟨ m | V (t) | n ⟩ ， ω_{m n} \equiv \frac{E_{m} - E_{n}}{ℏ} = - ω_{n m} \end{matrix}

式(9)を行列で表すならば次となる：

\begin{matrix} (11) & i ℏ (\begin{matrix} {\dot{c}}_{1} \\ {\dot{c}}_{2} \\ {\dot{c}}_{3} \\ ⋮ \end{matrix}) = (\begin{array}{cccc} V_{11} & V_{12} e^{i ω_{12} t} & \dots \\ V_{21} e^{i ω_{21} t} & V_{22} & \dots \\ V_{33} \\ ⋮ & ⋮ & ⋱ \end{array}) (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \\ ⋮ \end{matrix}) \end{matrix}

この式は, 系が状態

| n ⟩

に見出される確率を

t

の関数として求めるための基本的な微分方程式である．

時間に依存する２準位問題：核磁気共鳴やメーザーなど

時間依存するポテンシャル問題で厳密に解けるものは稀にしか存在しない．連立方程式(11)を解くには, 多くの場合は摂動展開に頼るしかない．しかし実際上大変重要でしかも厳密に解ける問題が一つある．それは「正弦的振動ポテンシャルを持つ２準位問題」である．
　この問題は $H_{0}$ と $V (t)$ が次で定義されるような問題である：

\begin{aligned} (12) & H_{0} & = E_{1} | 1 ⟩ ⟨ 1 | + E_{2} | 2 ⟩ ⟨ 2 |, V (t) = γ e^{i ω t} | 1 ⟩ ⟨ 2 | + γ e^{- i ω t} | 2 ⟩ ⟨ 1 |, (E_{2} > E_{1}) \end{aligned}

ただし

γ

と

ω

は正の実数である．このとき基礎ケットの規格直行性や式(8)から,

\begin{aligned} H_{0} | 1 ⟩ & = (E_{1} | 1 ⟩ ⟨ 1 | + E_{2} | 2 ⟩ ⟨ 2 |) | 1 ⟩ = E_{1} | 1 ⟩ ⟨ 1 | 1 ⟩ + E_{2} | 2 ⟩ ⟨ 2 | 1 ⟩ = E_{1} | 1 ⟩, H_{0} | 2 ⟩ = E_{2} | 2 ⟩, \\ V_{11} & = ⟨ 1 | V (t) | 1 ⟩ = ⟨ 1 | (γ e^{i ω t} | 1 ⟩ ⟨ 2 | + γ e^{- i ω t} | 2 ⟩ ⟨ 1 |) | 1 ⟩ = 0, \\ V_{12} & = ⟨ 1 | V (t) | 2 ⟩ = ⟨ 1 | (γ e^{i ω t} | 1 ⟩ ⟨ 2 | + γ e^{- i ω t} | 2 ⟩ ⟨ 1 |) | 2 ⟩ = γ e^{i ω t} ⟨ 1 | 1 ⟩ ⟨ 2 | 2 ⟩ = γ e^{i ω t}, \\ V_{21} & = ⟨ 2 | V (t) | 1 ⟩ = ⟨ 2 | (γ e^{i ω t} | 1 ⟩ ⟨ 2 | + γ e^{- i ω t} | 2 ⟩ ⟨ 1 |) | 1 ⟩ = γ e^{- i ω t} ⟨ 2 | 2 ⟩ ⟨ 1 | 1 ⟩ = γ e^{- i ω t}, \\ V_{22} & = ⟨ 2 | V (t) | 1 ⟩ = ⟨ 1 | (γ e^{i ω t} | 1 ⟩ ⟨ 2 | + γ e^{- i ω t} | 2 ⟩ ⟨ 1 |) | 2 ⟩ = 0, \end{aligned}

従って,この場合の摂動ポテンシャル

V

の行列要素は次であると言える：

\begin{matrix} (13) & V_{21} = V_{12}^{*} = γ e^{- i ω t}, V_{11} = V_{22} = 0 \end{matrix}

このとき, 時間依存するポテンシャル

V (t)

は

H_{0}

の２つのエネルギー固有状態を結ぶ作用を持っているので，２準位間の遷移

| 1 ⟩ ⟺ | 2 ⟩

が起こり得ることになる．
　この問題では厳密解が利用できる．

t = 0

の初期状態で, 系は低い方の準位のみが占められているとする：

\begin{matrix} (14) & c_{1} (0) = 1, c_{2} (0) = 0 \end{matrix}

すると式(11)から得られる次の連立方程式を解けばよい：

\begin{aligned} i ℏ \frac{d}{d t} c_{1} & = V_{11} (t) c_{1} + V_{12} e^{i ω_{12} t} c_{2} = V_{12} e^{- i ω_{21} t} c_{2} = γ e^{i ω t} e^{- i ω_{21} t} c_{2} \\ (15) & = γ e^{i (ω - ω_{12}) t} c_{2} \\ i ℏ \frac{d}{d t} c_{2} & = V_{21} (t) e^{i ω_{21} t} c_{1} + V_{22} c_{2} = V_{21} e^{i ω_{21} t} c_{1} = γ e^{- i ω t} e^{i ω_{21} t} c_{1} \\ (16) & = γ e^{- i (ω - ω_{12}) t} c_{1} \end{aligned}

ただし

ω_{21} = (E_{2} - E_{1}) / ℏ = - ω_{21}

である．第２式を更に時間微分したものに第１式を代入することで, 次のような

c_{2}

についての2次の定数係数の線形同次方程式が得られる：

\begin{matrix} (17) & {\ddot{c}}_{2} + i (ω - ω_{21}) {\dot{c}}_{2} + a^{2} c_{2} = 0, た だ し a = \frac{γ}{ℏ} \end{matrix}

これを初期条件

c_{2} (0) = 0

{\dot{c}}_{2} (0) = - i a

で解けばよい．その結果次の解が得られる：

\begin{matrix} (18) & c_{2} (t) = \frac{- 2 i \frac{γ}{ℏ} e^{- i (ω - ω_{21}) t / 2}}{\sqrt{(ω - ω_{21})^{2} + 4 {(\frac{γ}{ℏ})}^{2}}} \sin (\frac{\sqrt{(ω - ω_{21})^{2} + 4 {(\frac{γ}{ℏ})}^{2}}}{2} t) \end{matrix}

よって, 系がその後で２準位状態の各々に見出される確率は次で与えられる：

\begin{aligned} | c_{2} (t) |^{2} & = \frac{γ^{2} / ℏ^{2}}{\frac{γ^{2}}{ℏ^{2}} + \frac{(ω - ω_{21})^{2}}{4}} \sin^{2} (\sqrt{\frac{γ^{2}}{ℏ^{2}} + \frac{(ω - ω_{21})^{2}}{4}} t), \\ (19) & | c_{1} (t) |^{2} & = 1 - | c_{2} (t) |^{2}, た だ し ω_{21} \equiv \frac{E_{2} - E_{1}}{ℏ} \end{aligned}

これは, 分子線技術の父である I.I.ラビの名を取り, 「ラビの公式」と呼ばれている．
　式(19)の第1式から, エネルギー

E_{2}

の高い準位に系を見出す確率

| c_{2} (t) |^{2}

は, 次の角振動数の2倍で振動する時間依存性を示すことが分かる：

\begin{matrix} (20) & Ω = \sqrt{\frac{γ^{2}}{ℏ^{2}} + \frac{(ω - ω_{21})^{2}}{4}} \end{matrix}

また振動の振幅は，

\sin^{2}

の係数部分から角振動数

ω

が次の場合に最大となることが分かる：

\begin{matrix} (21) & ω ≃ ω_{21} \equiv \frac{E_{2} - E_{1}}{ℏ} \end{matrix}

こうなるのは普通, 外部から受ける電場や磁場によるポテンシャルの角振動数が２準位系を特徴づける角振動数とほぼ等しいときである．そのため, 等式(21)は「共鳴条件」と呼ばれている．
　共鳴点すなわち

ω = ω_{21}, Ω = γ / ℏ

のとき, 確率

| c_{1} (t) |^{2} $ と $ | c_{2} (t) |^{2}

を時間

t

に対してプロットすると次の図1 のようになり, 吸収と放出が交互に繰り返されることが分かる．

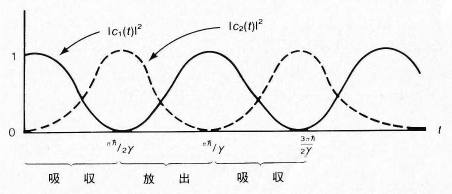
図 1. ちょうど共鳴していて $ω = ω_{21}, Ω = γ / ℏ$ である時の $| c_{1} (t) |^{2}$ と $| c_{2} (t) |^{2}$ を時間に対して描いたグラフ．系の状態は, 固有状態 $| 1 ⟩$ と $| 2 ⟩$ の間を往復することが分かる．

　また, 吸収-放出サイクルは共鳴点から離れていても起こっている．しかし式(15)からその振動振幅は減っている．今度は確率 $| c_{2} (t) |^{2}$ を角振動数 $ω$ の関数としてプロットすると図2 のようになり, 曲線は $ω = ω_{21}$ の周りを中心とした共鳴のピークを持ち, 半値幅の全幅は $4 γ / ℏ$ となる．また, それはポテンシャル $V (t)$ が弱い程 ( $γ$ が小さい程), 共鳴ピークが狭くなる．

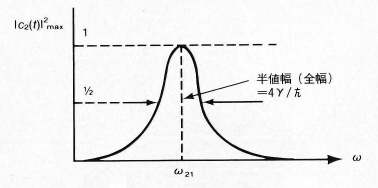
図 2. $| c_{2} (t) |^{2}$ を角振動数 $ω$ の関数として描いたグラフ．

スピン磁気共鳴

式(12)で定義される２準位問題には, 数多くの物理的応用がある．その例としてスピン $1 / 2$ の系 — 例えば原子核中の陽子 — が時間に依らない一様な $z$ -方向の磁場中に在り, 更に $x y$ -平面内を回転する時間依存する磁場も印加されている場合を考える：

\begin{matrix} (22) & B = B_{0} + B_{1} (t) = B_{0} \hat{z} + B_{1} (\hat{x} \cos ω t + \hat{y} \sin ω t) \end{matrix}

ただし

B_{0}, B_{1}

は定数である．時間依存性のない一様な磁場の効果を

H_{0}

とし, 回転磁場の効果は摂動項

V (t)

と見做して取り扱うことが出来る．磁気モーメント

μ

は次式で表された：

\begin{matrix} (23) & μ = \frac{e}{m_{e} c} S, S = \frac{ℏ}{2} σ \end{matrix}

よって

H_{0}

と

V (t)

は次のように表すことが出来る：

\begin{aligned} H_{0} & = - μ \cdot B_{0} = - \frac{e}{m_{e} c} S \cdot \hat{z} B_{0} = - \frac{e B_{0}}{m_{e} c} S_{z} \\ = - \frac{e B_{0}}{m_{e} c} \cdot \frac{ℏ}{2} (| + ⟩ ⟨ + | - | - ⟩ ⟨ - |) \\ V (t) & = - μ \cdot B_{1} = - \frac{e}{m_{e} c} S \cdot (\hat{x} B_{1} \cos ω t + \hat{y} B_{1} \sin ω t) \\ = - \frac{e B_{1}}{m_{e} c} (S_{x} \cos ω t + S_{y} \sin ω t) \\ (24) & = - \frac{e B_{1}}{m_{e} c} \cdot \frac{ℏ}{2} [\cos ω t (| + ⟩ ⟨ - | + | - ⟩ ⟨ + |) + \sin ω t (- i | + ⟩ ⟨ - | + i | - ⟩ ⟨ + |)] \end{aligned}

この時，

\begin{aligned} H_{0} | + ⟩ & = - \frac{e ℏ B_{0}}{2 m_{e} c} (| + ⟩ ⟨ + | - | - ⟩ ⟨ - |) | + ⟩ = - \frac{e ℏ B_{0}}{2 m_{e} c} | + ⟩ \equiv E_{+} | + ⟩ \\ (25) & H_{0} | - ⟩ & = - \frac{e ℏ B_{0}}{2 m_{e} c} (| + ⟩ ⟨ + | - | - ⟩ ⟨ - |) | - ⟩ = + \frac{e ℏ B_{0}}{2 m_{e} c} | - ⟩ \equiv E_{-} | - ⟩ \end{aligned}

従って,

\begin{matrix} (26) & E_{-} = \frac{e ℏ B_{0}}{2 m_{e} c}, E_{+} = - \frac{e ℏ B_{0}}{2 m_{e} c}, E_{-} > E_{+} \end{matrix}

よって, 陽子の場合では

E_{-}

は

E_{+}

よりもエネルギーが高いので, 式(12)の記法と対応させると,

\begin{matrix} (27) & | + ⟩ \to | 2 ⟩, | - ⟩ \to | 1 ⟩, E_{-} \to E_{2}, E_{+} \to E_{1} \end{matrix}

のように同定できる．そして, この２準位系を特徴づける角振動数は,

\begin{matrix} (28) & ω_{21} = \frac{E_{-} - E_{+}}{ℏ} = \frac{E_{-}}{ℏ} - \frac{E_{+}}{ℏ} = \frac{e B_{0}}{2 m_{e} c} + \frac{e B_{0}}{2 m_{e} c} = \frac{e B_{0}}{m_{e} c} \end{matrix}

であり, これはスピン歳差運動の角振動数に相当している．

z

-軸の正方向から見て反時計回りのスピン歳差運動によって期待値

⟨ S_{x} ⟩

⟨ S_{y} ⟩

は変化するが, 回転磁場

B_{1}

が無ければ確率

| c_{+} |^{2}

と

| c_{-} |^{2}

はいつまで経っても変化しない．しかし回転磁場が存在すると,

\begin{aligned} V_{- +} & = ⟨ - | V (t) | + ⟩ = - \frac{e ℏ B_{1}}{2 m_{e} c} (\cos ω t - i \sin ω t) | + ⟩ ⟨ - | + (\cos ω t + i \sin ω t) | - ⟩ ⟨ + | \\ = - \frac{e ℏ B_{1}}{2 m_{e} c} e^{i ω t} | - ⟩ ⟨ + | - \frac{e ℏ B_{1}}{2 m_{e} c} e^{- i ω t} | + ⟩ ⟨ - | \\ (29) & \equiv γ_{r o t} e^{i ω t} | - ⟩ ⟨ + | + γ_{r o t} e^{- i ω t} | + ⟩ ⟨ - | \end{aligned}

これは前述の式(13)に対応する式であるから, 確率

| c_{+}^{2} |

と

| c_{-}^{2} |

とが前図2のように時間の関数として変化することになる．このとき式(12)の記法に対応させて,

\begin{matrix} (30) & γ_{r o t} \to - \frac{e ℏ B_{1}}{2 m_{e} c}, ω \to ω \end{matrix}

と置くことが出来る．これはスピン

1 / 2

の系がスピンの歳差運動に加えて, スピンの反転

| + ⟩ \leftrightarrow | - ⟩

を繰り返していることを示している．半古典的には, このようなスピン反転は回転場

B_{1} (t)

によって引き起こされるトルクのためであると解釈できる．
　共鳴条件は, 回転磁場の振動数

ω

が, 一様な磁場の強さ

B_{0}

により決まる式(24)のスピン歳差振動数

ω_{21}

と一致すれば, いつでも満足される．この時スピン反転の確率は特に大きいことが分かる．
　回転磁場を作るのは困難であるが, 実際の実験では水平に振動する磁場 —例えば

x

-方向の磁場— で十分に実現することが出来る．これは, そのような振動磁場は反時計回りの成分と時計回りの成分に分解できることにまず注目する：

\begin{aligned} 2 B_{1} \hat{x} \cos ω t & = B_{1} (\hat{x} \cos ω t + \hat{y} \sin ω t) + B_{1} (\hat{x} \cos ω t - \hat{y} \sin ω t) \\ (31) & = B_{1} (\hat{x} \cos ω t + \hat{y} \sin ω t) + B_{1} (\hat{x} \cos (- ω t) + \hat{y} \sin (- ω t)) \end{aligned}

このとき第2項目は時計回りの項になっている．共鳴条件が反時計回りの成分に対して満されているとしよう：

\begin{matrix} (32) & ω ≃ ω_{21} \end{matrix}

典型的な実験条件下では

B_{1} ≪ B_{0}

である．これを式(25)の

γ_{r o t}

で表現するならば,

\begin{matrix} (33) & | \frac{γ_{r o t}}{ℏ} | = \frac{e B_{1}}{2 m_{e} c} ≪ ω_{21} = \frac{e B_{0}}{2 m_{e} c} \end{matrix}

この結果, 共鳴条件が反時計回り成分に対して満たされているときはいつも, 時計回り成分の効果は完全に無視できる．なぜなら, 時計回り成分に対しては

ω \to - ω

となるから, 式(15)の振幅の大きさは小さく, また角振動数はずっと大きくなって非常に早く振動するからである：

\begin{matrix} (34) & | c_{+}^{2} | ≃ {\begin{cases} \sin^{2} \frac{γ}{ℏ} t & when counterclockwise \\ \frac{1}{1 + \frac{ℏ^{2} (ω + ω_{21})^{2}}{4 γ^{2}}} \sin^{2} (\frac{γ^{2}}{ℏ^{2}} + \frac{(ω + ω_{21})^{2}}{4} t) & when clockwise \end{cases} \end{matrix}

　ここで解いた共鳴の問題は, 原子分子線や核磁気共鳴の実験を解釈する際に基礎となる重要な問題である．振動磁場の振動数を変化させることで, 磁気モーメントの非常に精密な測定をすることが可能である．
　一般に時間を含む２準位系の問題には, 他の原子時計や光学的ポンピングといった多くの応用がある．実際, 物理部門のノーベル賞が4件も, 時間を含むある種の２準位系を研究した人々に与えられた．２準位系の共鳴を扱ってノーベル賞を受賞した人達は, 分子線と核磁気共鳴に対してラビ(1944), 原子核に於ける

B

場と核磁気モーメントに対してブロッホとパーセル(1952), メーザーとレーザー及び量子光学に対してタウンズ, バソフ及びプロチョロフ(1954), 光学的ポンピングに対してカストラー(1966)である．

時間を含む摂動論

前節で扱った時間に依存する２準位問題のような少数の問題は例外にして， $c_{n} (t)$ に対する微分方程式の厳密解は通常は求められない．よって前節の式(11)の近侍解として, 次式のように摂動展開で得られるもので満足しなければならない：

\begin{matrix} (35) & c_{n} (t) = c_{n}^{(0)} (t) + c_{n}^{(1)} (t) + c_{n}^{(2)} (t) + \dots \end{matrix}

ただし

c_{n}^{(i)} (t)

は, 時間に依存するポテンシャルの大きさのパラメータに関して, 1次, 2次,

\dots

の振幅を表わす．この時間を含む摂動展開は1927年にディラックが発展させたものである．
　

c_{n} (t)

の摂動展開を直接考える代わりに, 相互作用表示での時間発展演算子

U_{I} (t, t_{0})

の摂動展開をまず求め, その行列要素を

c_{n} (t)

と関係付けることでその摂動展開を求めることが出来る．相互作用表示での時間発展演算子は次で定義される：

\begin{matrix} (36) & | α, t ⟩ = U_{I} (t, t_{0}) | α, t_{0} ⟩_{I} \end{matrix}

そこで始状態のシュレディンガー表示での状態ケットを

| i, t_{0} ⟩_{S} = e^{- i E_{i} t_{0}} | i ⟩

とすると, 相互作用表示での始状態ケットは簡単な形：

| i, t_{0} ⟩_{I} = | i ⟩

となる．そして, 時間

t

後での状態ケットは次で与えられる：

\begin{matrix} (37) & | i, t ⟩_{I} = U_{I} (t, t_{0}) | i ⟩ = \sum_{n} c_{n} (t) | n ⟩ \end{matrix}

これに左から基礎ブラ

⟨ n |

を作用させることで，

c_{n} (t)

は次のように求められることになる：

\begin{matrix} (38) & c_{n} (t) = ⟨ n | U_{I} (t, t_{0}) | i ⟩ \end{matrix}

相互作用表示での状態ケットに対する微分方程式(5)は次と同値である：

\begin{matrix} (39) & i ℏ \frac{d}{d t} U_{I} (t, t_{0}) = V_{I} (t) U_{I} (t, t_{0}) \end{matrix}

この演算子に対する微分方程式を, 初期条件

\begin{matrix} (40) & U_{I} (t, t_{0}) |_{t = t_{0}} = 1 \end{matrix}

で解く必要がある．するとこれは次の積分方程式と同値であることになる：

\begin{matrix} (41) & U_{I} (t, t_{0}) = 1 - \frac{i}{ℏ} \int_{t_{0}}^{t} V_{I} (t^{'}) U_{I} (t^{'}, t_{0}) d t^{'} \end{matrix}

この近似解は, 逐次近似の方法により次のように求められる：

\begin{aligned} U_{I} (t, t_{0}) & = 1 - \frac{i}{ℏ} \int_{t_{0}}^{t} V_{I} (t^{'}) [1 - \frac{i}{ℏ} \int_{t_{0}}^{t^{‘}} V_{I} (t^{”}) U_{I} (t^{”}, t_{0}) d t^{”}] d t^{'} \\ = 1 - \frac{i}{ℏ} \int_{t_{0}}^{t} V_{I} (t^{'}) d t^{'} + {(- \frac{i}{ℏ})}^{2} \int_{t_{0}}^{t} d t^{'} \int_{t_{0}}^{t^{‘}} d t^{”} V_{I} (t^{'}) V_{I} (t^{”}) \\ (42) & + \dots + {(- \frac{i}{ℏ})}^{2} \int_{t_{0}}^{t} d t^{'} \int_{t_{0}}^{t^{‘}} d t^{”} \dots \int_{t_{0}}^{t^{(n - 1)}} d t^{n} V_{I} (t^{'}) V_{I} (t^{”}) \dots V_{I} (t^{(n)}) + \dots \end{aligned}

この級数は, この方法を共変的量子電気力学(QED) に応用したフリーマン・ダイソンの名に因んで, 「ダイソン級数」と呼ばれている．
　式(38)に式(42)を代入すると，

c_{n} (t)

の摂動展開の各々の項を得ることが出来る：

\begin{aligned} c_{n}^{(0)} & = δ_{n i} (t に依存しない) \\ c_{n}^{(1)} & = - \frac{i}{ℏ} \int_{t_{0}}^{t} ⟨ n | V_{I} (t^{'}) | i ⟩ d t^{'} = - \frac{i}{ℏ} \int_{t_{0}}^{t} e^{i ω_{n i} t^{'}} V_{n i} (t^{'}) d t^{'} \\ (43) & c_{n}^{(2)} & = {(- \frac{i}{ℏ})}^{2} \sum_{m} \int_{t_{0}}^{t} d t^{'} \int_{t_{0}}^{t^{'}} d t^{”} e^{i ω_{n m} t^{'}} V_{n m} (t^{'}) e^{i ω_{m i} t^{”}} V_{m i} (t^{”}) \\ ⋮ \end{aligned}

始状態

| i ⟩

から終状態

| n ⟩

へ移る遷移確率は，

n \neq i

として次式で与えられる：

\begin{matrix} (44) & P (i \to n) = | c_{n}^{(1)} (t) + c_{n}^{(2)} (t) + \dots | \end{matrix}

2025年5月
月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31