高次の項 (The Higher-order Terms) の文章について

問題 6-26 の次に書かれている「高次の項(The Higher-order Terms)」の文章が少し分かりづらいと感じたので, その部分を翻訳してそれに自分なりの補足を付加したもの(補足した部分は鍵カッコで囲み灰色で色付けした)を示しておこう．

▼ 高次の項　摂動展開に於ける2次の項を見ることは興味深い．この2次の項が特に重要となるのは,注目する特定な状態 $m$ と $n$ に対して $V_{m n} = 0$ であるような問題のときである．そのような問題が存在するとし, さらにそのとき $V_{k n} \neq 0$ となるような他の状態 $k \neq n$ も存在すると仮定しよう．1次の項はゼロである．そして $n \neq m$ である限り 0次の項もやはりゼロである．従って, この問題で遷移振幅の計算に入って来る最低次の項は 2次の項となる．[ 例えば, 第9章の荷電粒子と電磁場との相互作用の場合では, § 9.6 「Lambシフト」の議論がこの場合に相当する．従って, 「Lambシフト」での摂動補正は 2次近似で生じるので, ここでの議論を用いる必要がある．]
ポテンシャル $V$ が $t$ に依存しないものとする [ 従って行列要素 $V_{m k}, V_{k n}$ は時間積分の外に出せる]．すると遷移振幅の2次の項は $λ_{m n}^{(2)}$ である．従って $T = t_{2} - t_{1}$ とすると, それは式 (6-74) から次式となる：

\begin{aligned} e^{+ i (E_{m} t_{2} - E_{n} t_{1}) / ℏ} λ_{m n}^{(2)} & = {(- \frac{i}{ℏ})}^{2} \sum_{k} V_{m k} V_{k n} \int_{0}^{T} d t_{4} e^{i (E_{m} - E_{k}) t_{4} / ℏ} \int_{0}^{t_{4}} d t_{3} e^{i (E_{k} - E_{n}) t_{3} / ℏ} \\ = (\frac{- i}{ℏ}) \sum_{k} V_{m k} V_{k n} \int_{0}^{T} d t_{4} e^{i ω_{m k} t_{4}} \frac{1 - e^{i ω_{k n} t_{4}}}{ℏ ω_{k n}} \\ = \sum_{k} \frac{V_{m k} V_{k n}}{ℏ ω_{k n}} (\frac{1 - e^{i ω_{m k} T}}{ℏ ω_{m k}} - \frac{1 - e^{i ω_{m n} T}}{ℏ ω_{m n}}) \\ (6-98) & = \sum_{k} \frac{V_{m k} V_{k n}}{E_{k} - E_{n}} (\frac{e^{i (E_{m} - E_{n}) T / ℏ} - 1}{E_{m} - E_{n}} - \frac{e^{i (E_{m} - E_{k}) T / ℏ} - 1}{E_{m} - E_{k}}) \end{aligned}

【参考】上式は,

ω_{k n} = (E_{k} - E_{n}) / ℏ

としたときの次の積分結果, 及び関係

ω_{m k} + ω_{k n} = ω_{m n}

を用いている：

\begin{aligned} (\frac{- i}{ℏ}) \int_{0}^{t} d t^{‘} e^{i ω_{k n} t^{‘}} & = (\frac{- i}{ℏ}) {[\frac{e^{i ω_{k n} t^{‘}}}{i ω_{k n}}]}_{0}^{t} = (\frac{- i}{ℏ}) \frac{e^{i ω_{k n} t} - 1}{i ω_{k n}} = \frac{1 - e^{i ω_{k n} t}}{ℏ ω_{k n}} \\ = \frac{1 - e^{i (E_{k} - E_{n}) t / ℏ}}{E_{k} - E_{n}} \end{aligned}

この結果の最後の因子に於ける2つの項の内, 初めの項は1次の結果で見たものと同じ時間依存性を持つ．従って, 当面2番目の項を無視すると, 結果は前と同じように「

E_{m} = E_{n}

を満たす状態間のみで遷移が起こる」ことになり, その確率は

T

に比例する．単位時間当たりの確率は式(6-86) と同様な形であり

M_{n \to m}

を,

\begin{matrix} (6-99) & M_{n \to m} = \sum_{k} \frac{V_{m k} V_{k n}}{E_{k} - E_{n}} \end{matrix}

で置き換えたものになっている．状態が連続スペクトルの中にあるものとすると, 和は積分となる．
【参考】 1次の場合では, 遷移振幅は式 (6-78) となるのだった：

\begin{matrix} (6-78) & λ_{m n}^{(1)} e^{i (E_{m} t_{2} - E_{n} t_{1}) / ℏ} = V_{m n} \frac{1 - e^{i (E_{m} - E_{n}) T / ℏ}}{E_{m} - E_{n}} \end{matrix}

この式で

- V_{m n}

を式 (6-99) で置き換えると式 (6-98) の第1項の形となる．そして遷移確率

P (n \to [m])

は1次の場合, 式 (6-85) のように

T

に比例し, 従って「遷移率」

w_{n \to [m]}

は式 (6-86) の形に表せるのであった：

P (n \to [m]) = \frac{2 π}{ℏ} | V_{m n} |^{2} ρ (E_{m}) T |_{E_{m} ≃ E_{n}}, w_{n \to [m]} = \frac{2 π}{ℏ} | M_{n \to [m]} |^{2} ρ (E_{m}) |_{E_{m} ≃ E_{n}}

この遷移確率

P (n \to [m])

と遷移率

w_{n \to [m]}

の形と式 (6-98) の第1項とを比較するならば, ただ

| V_{m n} |^{2}

を式 (6-99) の

| M_{n \to m} |^{2}

で置き換えるだけでよく, その結果式は1次のときと同様な解釈ができる訳である．
式 (6-99) が正しいのは, 初期状態

n

から特定な状態

m

への遷移も, また初期状態と同じエネルギーを持ったどんな状態

k

への遷移も, 1次遷移では不可能であるという状況のときである．そのような状況では

E_{k} = E_{n}

となる状態間に対しては

V_{k n} = 0

である [ 仮定から当然である ]．すると式 (6-98) 括弧内の第2項は決して大きくならない．なぜなら, 分母

E_{m} - E_{k}

がほぼゼロでない限りこの項は大きく成り得ないが, そのとき [ 遷移は

E_{m} = E_{n}

を満たす状態間のみで起こり, かつ

E_{n}

と同じエネルギー状態

k

への1次遷移も不可能であるとすると, 結局

E_{m}

と同じエネルギー状態

k

への1次遷移も不可能と言えるから ] 分子の

V_{m k}

はゼロだからである．よって全ての効果は第1項から由来するため, 式 (6-99) は正しい．さらに式 (6-98) の

k

についての和に於いて,

E_{k} = E_{m}

の所での極に曖昧さはない．なぜなら

E_{k}

がその値のときには, 分子もゼロとなるからである．
【参考】原書では, 上記の青色部分が

E_{n} - E_{k}

及び

V_{k n}

となっている．しかしこれはミスプリントではないかと思われた？そこで, ここでは本文の記述を変更して書いたので注意する．また

E_{k}

が

E_{n}

とも

E_{m}

とも異なる場合には

ω_{m k} = (E_{m} - E_{k}) / ℏ \neq 0

となるが, その場合第2項目は

ω_{m k}

の増大と共に速く振動する減衰振動となり,

T

と共に増大する遷移確率にはやはり寄与することはない (J.J.Sakurai より)．

他方, ある状況下では, ある別の連続状態へ一次遷移出来るということも真となり得よう (例えば, 原子核は一つ以上のやり方で崩壊可能である)．そのような場合, 式 (6-99) の和は無意味である．なぜなら,「極の近傍では何をすべきか」を定義する必要があるからである．ここで助けてくれるのが式 (6-98) で無視した第2項目である．それにより $ε \to 0$ の極限に於ける $M_{n \to m}$ の正しい表現が, 次式となることを示してくれる (ただし一般化のために今度は 1次の項も含めている)：

\begin{matrix} (6-100) & M_{n \to m} = V_{m n} + \sum_{k} \frac{V_{m k} V_{k n}}{E_{k} - E_{n} - i ε} \end{matrix}

これがどのようにして出てくるのかを以下で分析して行く．
まず最初に気付くことは, 大きな

T

では,

E_{n}

と

E_{m}

が (

ℏ / T

の周りの範囲内では) 実質的に等しい場合以外では, 大きな遷移確率 (すなわちそれは

T

に比例する) を得ることが出来ないということである．式 (6-98) の最初の項ではこれは明らかである． [ 図 6-13 を書き直した下図1 と同じような変化をするので, 摂動が印加されている時間を

T

とするならば, 比較的大きな確率を持つ遷移が可能なのは

T Δ E \sim π ℏ

のときのみである．このときエネルギー変化の範囲はおよそ

- π ℏ / T \leq Δ E \leq π ℏ / T

と言える．摂動が長い時間

T

だけ掛かっているときは, ピークの幅は狭くなり, 比較的大きな確率の遷移が可能なのは近似的にエネルギーが保存されるときである．そのとき

w = 0

の周りの中央ピークは高さが

T^{2}

で幅が

1 / T

に比例しているので, その面積は大体

T

に比例したものとなる]．

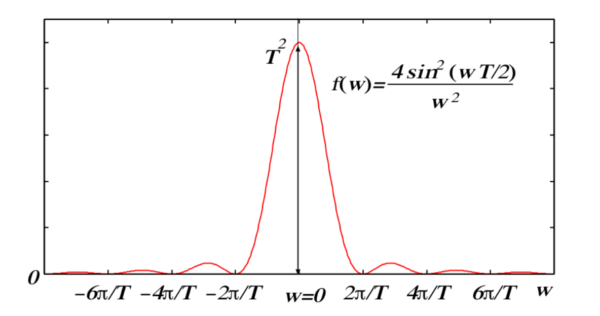
図 1. この図では, エネルギー差 $E_{m} - E_{n}$ は変数 $w = (E_{m} - E_{n}) / ℏ$ で置き換えてある．これらのエネルギーがほぼ等しいとき (つまり $w$ が非常に小さいとき), 関数 $(s i n^{2} w T / 2) / w^{2}$ は最大値を取る．エネルギー差が大きいと, この関数は非常に小さくなる．よって, この関数を含む表式で, 最も重要な寄与は中央の $w = 0$ 周辺の領域から来る．すなわち， 2つのエネルギーがほぼ等しい領域から来るのである．

第2項目の場合では, 大きな振幅が生じるのは $E_{k} \approx E_{m}$ のときだけである．しかしもし $E_{m}$ が $E_{n}$ にあまり近くない場合には, 最初の因子は, $E_{k}$ が $E_{m}$ に近いとき $E_{k}$ の滑らかな関数である． [ 例えば, $Δ = E_{m} - E_{k} = E_{m} - E_{k} + E_{k} - E_{n} = x + ε$ , $x = E_{k} - E_{n}$ , $ε = E_{m} - E_{k}$ とすると, $Δ$ は微小ではないので $ε$ は微小量と見做せるが $x$ は小さくない．よって $f (x) = V_{m k} V_{k n} / x$ は滑らかな関数と考えることが出来る．そこで $x = E_{k} - E_{n}$ 自体は $E_{k}$ に依存はするが, $E_{k}$ が $E_{m}$ に近くに来たときでも $x$ は微小とはならず $f (x)$ が急激に変化することはしない]．よって, $E_{k} = E_{m}$ 近傍の小さな範囲ではそれをほぼ一定と見做してしまうならば,

\begin{aligned} - \sum_{k} (\frac{V_{m k} V_{k n}}{E_{k} - E_{n}}) \frac{e^{i (E_{m} - E_{k}) T / ℏ} - 1}{E_{m} - E_{k}} & ≃ - \int d E_{k} (\frac{V_{m k} V_{k n}}{E_{k} - E_{n}}) \frac{e^{i (E_{m} - E_{k}) T / ℏ} - 1}{E_{m} - E_{k}} \\ \approx (\frac{V_{m k} V_{k n}}{E_{k} - E_{n}}) \int (- d E_{k}) \frac{e^{i (E_{m} - E_{k}) T / ℏ} - 1}{E_{m} - E_{k}} \end{aligned}

[ よって, 上式で

ε = E_{m} - E_{k}

とおくと,

d ε = - d E_{k}

であるから], 第2項目は, 積分量に定数を掛け合わせたものとして近似できる：

f (x) \int d ε \frac{e^{i ε T / ℏ} - 1}{ε} = C \times \int \frac{e^{i ε T / ℏ} - 1}{ε} d ε

ただし

ε = (E_{m} - E_{k})

は, ある微小区間, 例えば

- δ

から

+ δ

で積分されるものとする．しかし [ 変数変換

y = ε T / ℏ

を行うと

ε = ℏ y / T

d ε = ℏ d y / T \to d ε / ε = d y / y

となるので],

\begin{aligned} \int_{- δ}^{+ δ} (e^{i ε T / ℏ} - 1) \frac{d ε}{ε} & = \int_{- T δ / ℏ}^{T δ / ℏ} (e^{i y} - 1) \frac{d y}{y} \\ = \int_{- T δ / ℏ}^{T δ / ℏ} (\cos y + i \sin y - 1) \frac{d y}{y} \\ (6-101) & = \int_{- T δ / ℏ}^{T δ / ℏ} (\frac{c o s y - 1}{y} + i \frac{\sin y}{y}) d y \end{aligned}

最初の積分は奇関数の積分なのでゼロとなる．2番目の積分は

T \to \infty

のとき (従って

T δ / ℏ \to \infty

のとき), ある有限な極値に近づく．すなわち,

i \int_{- \infty}^{\infty} \frac{\sin y}{y} d y = 2 i \int_{0}^{\infty} \frac{\sin y}{y} d y = π i

【参考】原書では最後の結果に因子

2

が書かれているがここではそれを除いた．なぜなら, 岩波の数学公式

I

のp.250 を参照すると, 次の公式が記してあったからである：

\int_{0}^{\infty} \frac{\sin a x}{x} d x = {\begin{cases} + \frac{π}{2}, & a > 0 \\ - \frac{π}{2} & a < 0 \end{cases}

従って大きな遷移確率は生じない．「

E_{n}

と

E_{m}

が本質的に等しい場合にのみ, 大きな影響が生じ得る」．その場合には,

(E_{k} - E_{n})^{- 1}

と

(E_{m} - E_{k})^{- 1}

由来の２つの極が二重に一致するので, そのことが第 2 項目を重要たらしめる．従って, 以下では「

E_{m}

と

E_{n}

はほぼ等しい」と仮定して分析を続けて行く．
式(6-98)中の

k

についての和は, 非常に小さなエネルギー

Δ

を選ぶことで２つの部分に別けることが出来る．そして和を

| E_{k} - E_{n} | \geq Δ

に対する部分

A

と

| E_{k} - E_{n} | \leq Δ

に対する部分

B

とに分割する[下図2.を参照]．

Δ

の大きさを選ぶには,

E_{k}

が

E_{n}

の周りでこのエネルギー範囲

2 Δ

に渉って変化するときに, 因子

V_{m k} V_{k n}

が感知できるほど変化しないよう十分小さいものとする．この

Δ

はある有限なエネルギーであり, 時間

T

は十分長く摂って

ℏ / T ≪ Δ

となるようにする．それは

| E_{n} - E_{m} | ≪ Δ

であることを意味している．

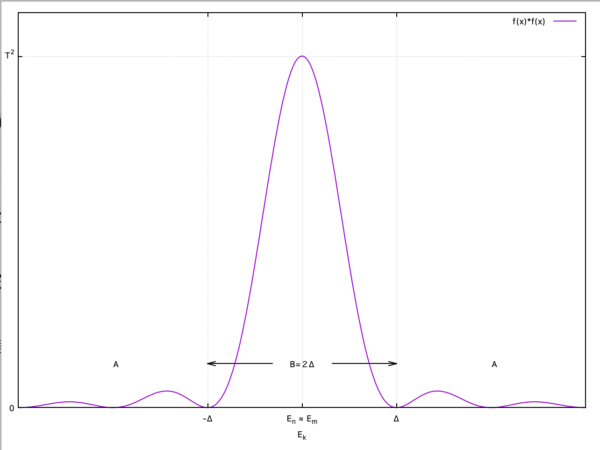
図 2. $E_{k} = E_{n} \approx E_{m}$ を中心に $[- Δ, Δ]$ の範囲を B とし,その外側の部分を A とする．

まず部分

A

では

| E_{k} - E_{m} | \geq Δ

である．このとき第2項目は大きくは成り得ない．なぜなら, 極が回避されるからである．よって第1項目だけが寄与し, その寄与値は次である：

\begin{matrix} (6-102) & \sum_{k}^{(A)} \frac{V_{m n} V_{k n}}{E_{k} - E_{n}} \frac{e^{i (E_{m} - E_{n}) T / ℏ} - 1}{E_{m} - E_{n}} \equiv a \frac{e^{i x} - 1}{x} \frac{T}{ℏ} \end{matrix}

ただし,

x = \frac{E_{m} - E_{n}}{ℏ} T, a = \sum_{k}^{(A)} \frac{V_{m k} V_{k n}}{E_{k} - E_{n}}

和は

E_{m}

の

\pm Δ

以内を除く全ての

E_{k}

に及ぶ．この和は

Δ

には殆ど依存しない．そして

Δ \to 0

のとき「主値積分」( principal-value integral ) の定義となる．即ち, 極限

Δ \to 0

で次のように書くことが出来る：

\begin{matrix} (6-103) & a = V_{m n} + \sum_{k} V_{m k} V_{k n} P . P . \frac{1}{E_{k} - E_{n}} \end{matrix}

ただし P.P. は主値部分を表している[前ブログ記事「複素積分の公式について」を参照のこと]．そして1次の項

V_{m n}

を回復させた．これは

V_{m n}

がゼロとならない場合を考慮したからである．
次に領域

B

の場合であるが, この場合の

V_{m k} V_{k n}

は,「

E_{k} - E_{m} = 0

のときの値であり一定である」と考える(take)．[そして前と同様に, 和は積分に置き換えて考える]：

\begin{aligned} \sum_{k}^{(B)} V_{m k} V_{k n} F (E_{k}) & = \sum_{k}^{(B)} \frac{V_{m k} V_{k n} δ (E_{k} - E_{m})}{E_{k} - E_{n}} (\frac{e^{i (E_{m} - E_{n}) T / ℏ} - 1}{E_{m} - E_{n}} - \frac{e^{i (E_{m} - E_{k}) T / ℏ} - 1}{E_{m} - E_{k}}) \\ \to \int d E_{k} \frac{V_{m k} V_{k n} δ (E_{k} - E_{m})}{E_{k} - E_{n}} (\frac{e^{i (E_{m} - E_{n}) T / ℏ} - 1}{E_{m} - E_{n}} - \frac{e^{i (E_{m} - E_{k}) T / ℏ} - 1}{E_{m} - E_{k}}) \end{aligned}

即ち,

\sum_{k}^{(B)} V_{m k} V_{k n} F (E_{k})

を次で置き換え, これを

b I

と書くことにする：

\begin{matrix} (6-104) & [\sum_{k} V_{m k} V_{k n} δ (E_{k} - E_{m})] \int_{E_{m} - Δ}^{E_{m} + Δ} F (E_{k}) d E_{k} \equiv b I \end{matrix}

ただし, [

E_{n}

と

E_{m}

は本質的に等しいので ]

\begin{matrix} (6-105) & b = \sum_{k} V_{m k} V_{k n} δ (E_{k} - E_{m}) = \sum_{k} V_{m k} V_{k n} δ (E_{k} - E_{n}) \end{matrix}

そして,

\begin{matrix} (6-106) & I = \int_{E_{m} - Δ}^{E_{m} + Δ} \frac{d E_{k}}{E_{k} - E_{n}} (\frac{e^{i (E_{m} - E_{n}) T / ℏ} - 1}{E_{m} - E_{n}} - \frac{e^{i (E_{m} - E_{k}) T / ℏ} - 1}{E_{m} - E_{k}}) \end{matrix}

さてここで

(E_{m} - E_{n}) (T / ℏ) = x

そして

(E_{k} - E_{n}) (T / ℏ) = y

とおく．
すると,

\begin{aligned} (E_{m} - E_{k}) \frac{T}{ℏ} = (E_{m} - E_{n} + E_{n} - E_{k}) \frac{T}{ℏ} = (E_{m} - E_{n}) \frac{T}{ℏ} - (E_{k} - E_{n}) \frac{T}{ℏ} = x - y, \\ \frac{d E_{k} (T / ℏ)}{(E_{k} - E_{n}) (T / ℏ)} = \frac{d y}{y}, \frac{1}{E_{m} - E_{n}} = (\frac{T}{ℏ}) \frac{1}{x}, \frac{1}{E_{m} - E_{k}} = (\frac{T}{ℏ}) \frac{1}{x - y}, \\ E_{k} - E_{m} ≃ E_{k} - E_{n} = \pm Δ \to y = (E_{k} - E_{n}) \frac{T}{ℏ} = \pm Δ \frac{T}{ℏ} \end{aligned}

従って次を得る：

\begin{matrix} (6-107) & I = \frac{T}{ℏ} \int_{- T Δ / ℏ}^{+ T Δ / ℏ} \frac{d y}{y} (\frac{e^{i x} - 1}{x} - \frac{e^{i (x - y)} - 1}{x - y}) \end{matrix}

この積分は

y

を複素変数と見做した周積分 (contour integral) を考え, 閉曲線を変化させることで非常に容易に評価することが出来る．

- T Δ / ℏ

から

T Δ / ℏ

までの直線上の積分の代わりに, 実軸より下を通る半径

T Δ / ℏ

の半円上の積分に移る(go on)．

T Δ / ℏ

は非常に大きいので, 第2項の寄与は無視できる．従って, この閉曲線上で [

f (x) = 1

の場合を考えると, そのときの主値はゼロなので]

\begin{aligned} \oint_{C} \frac{f (z)}{z - a} d z = P \int_{- \infty}^{\infty} \frac{f (x)}{x - a} d x ＋ i π f (a), \to \int_{- \infty}^{\infty} \frac{1}{x - a} d x = 0 + i π = i π \\ \Rightarrow \int_{- T Δ / ℏ}^{T Δ / ℏ} \frac{d y}{y} \approx \int_{- \infty}^{\infty} \frac{d y}{y} = i π \end{aligned}

となるので

I

は次となる：

I \approx \frac{T}{ℏ} \frac{e^{i x} - 1}{x} \int_{- T Δ / ℏ}^{T Δ / ℏ} \frac{d y}{y} = i π \frac{T}{ℏ} \frac{e^{i x} - 1}{x}

部分 A と部分 B とを一緒にすることで, [即ち式 (6-102) と式 (6-105) 及び式 (6-107) から振幅は

x ≪ 1

として] 次となる：

\begin{aligned} a \frac{e^{i x} - 1}{x} \frac{T}{ℏ} + b I & = a \frac{T}{ℏ} \frac{e^{i x} - 1}{x} + i π b \frac{T}{ℏ} \frac{e^{i x} - 1}{x} \\ (6-108) & = (a + i π b) \frac{T}{ℏ} \frac{e^{i x} - 1}{x} \end{aligned}

[ここで, 式中の因子

(T / ℏ) (e^{i x} - 1) / x

は

x = (E_{m} - E_{n}) T / ℏ

であった．更に, このとき

E_{m} \approx E_{n}

であったから

E_{m} - E_{n} \approx x, (x ≪ 1)

と近似しても構わないであろう．更にまた, 式 (6-86) では

M_{n \to m}

の絶対値を取るので虚数単位

i

は無視してしまってよい．すると,]

\begin{aligned} \frac{T}{ℏ} \frac{e^{i x} - 1}{x} = \frac{e^{i x} - 1}{E_{m} - E_{n}} \approx \frac{e^{i x} - 1}{x} ≃ i (x ≪ 1), \\ \Rightarrow (a + i π b) \frac{T}{ℏ} \frac{e^{i x} - 1}{x} \approx (a + i π b) i \to a + i π b \end{aligned}

これにより, 式 (6-86) の形の遷移確率は

M_{n \to m}

を次としたものとなる：

\begin{aligned} M_{n \to m} & = a + i π b = V_{m n} + \sum_{k} V_{m k} V_{k n} P . P . \frac{1}{E_{k} - E_{n}} + i π \sum_{k} V_{m k} V_{k n} δ (E_{k} - E_{n}) \\ (6-109) & = V_{m n} + \sum_{k} V_{m k} V_{k n} [P . P . \frac{1}{E_{k} - E_{n}} + i π δ (E_{k} - E_{n})] \end{aligned}

最後の鍵カッコ部分は,

ε \to 0

の極限で

(E_{k} - E_{m} - i ε)^{- 1}

と書くことが出来る．[前ブログ「複素積分の公式について」の式(9)で

x \to E_{k}, a \to E_{n}

とした場合になる]：

\begin{matrix} (9) & lim_{ε \to 0} \frac{1}{x - a - i ε} = P \frac{1}{x - a} d x + i π δ (x - a) \end{matrix}

よって

M_{n \to m}

は, 式 (6-100) の形に書くことが出来たことになる：

\begin{aligned} M_{n \to m} & = V_{m n} + \sum_{k} V_{m k} V_{k n} [P . P . \frac{1}{E_{k} - E_{n}} + i π δ (E_{k} - E_{n})] \\ (6-100) & = V_{m n} + \sum_{k} V_{m k} V_{k n} \frac{1}{E_{k} - E_{n} - i ε} \end{aligned}

式 (6-100) から,

n

から

m

への直接的な遷移がそのときには不可能であっても,「仮想状態」(virtual state)と呼ばれる状態を通じて遷移は可能であることが分かる．即ち, 系は

n

から

k

へ, そして

k

から

m

へと遷移すると考えることが出来る．
間接的な遷移過程の遷移振幅は式 (6-99) で与えられている．「系は実際に一つまたは別の中間状態

k

を経るというのではなく, むしろ量子力学に特徴的なこととして、様々な中間状態

k

を経る振幅があって, その寄与が干渉を起こすと言うのが正しい」ことに注意する．
中間状態は始状態や終状態と同じエネルギー状態ではない．しかしエネルギー保存は破掟していない．なぜなら, 仮想状態は永久的に占有されるものではないからである．和への寄与の強さは, このエネルギー不一致量(discrepancy) に反比例して変化する．
これらの中間状態に絶対的なものは全く存在しない．それは,

V

を系

H

の摂動と考え,

H + V

の真の状態について

H

だけの状態で表現して見れば分かることである．無摂動問題と摂動問題の区別を別の仕方で行ったならば,その処方には異なる公式と中間状態が現れるであろう．
ポテンシャルが時間に (例えば周期的に) 依存する場合には, 多くの興味深い効果が起こる(result)．それらのほとんどは, マイクロ波実験に於いて観測される．その場合の摂動

V (x, t)

は, 周期的な時間変化をする弱い電場または磁場である．

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31