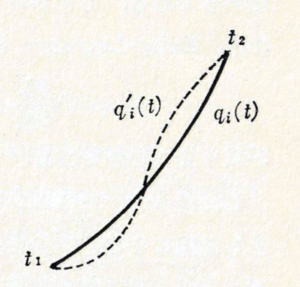\(\)
少しくどいとは思うが, ランダウ=リフシッツによる解析力学的なローレンツ力の導出法も示しておこう．
ランダウとリフシッツの肖像
最小作用の原理
力学系の運動法則の最も一般的な定式化は,「最小作用の原理」または「ハミルトンの原理」で与えられる．この原理に従えば, 各々の力学系はある特定な関数
\begin{equation}
L=L(q_{1},\,q_{2},\,\dotsb,\,q_{f},\dot{q}_{1},\,\dot{q}_{2},\,\dotsb,\,\dot{q}_{f})\equiv L(q,\dot{q},t)
\tag{1}
\end{equation}
L=L(q_{1},\,q_{2},\,\dotsb,\,q_{f},\dot{q}_{1},\,\dot{q}_{2},\,\dotsb,\,\dot{q}_{f})\equiv L(q,\dot{q},t)
\tag{1}
\end{equation}
によって特徴づけられる．その際, その系の運動は「時刻 \(t=t_1\) 及び \(t=t_2\) に, 系が２組の座標系 \(q^{(1)},\,q^{(2)}\) で示される位置に居た」という条件を満たすものとする．そのとき, これら２点間の系の運動は, 次の積分
\begin{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\odiff#1{\frac{d}{d #1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\ket#1{|#1\rangle}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
S\equiv \int_{t_{1}}^{t_{2}} L(q,\dot{q},t)\,dt
\tag{2}
\end{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\odiff#1{\frac{d}{d #1}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2}#1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\ket#1{|#1\rangle}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
S\equiv \int_{t_{1}}^{t_{2}} L(q,\dot{q},t)\,dt
\tag{2}
\end{equation}
が最小値を取るようなものとなる．このときの関数 \(L\) を, 与えられた系の「ラグランジアン」と言い, 積分 (2) を「作用(action)」という．
「積分 (2) を最小にする」という問題を解くための微分方程式を導こう．ただし系は自由度が１で一つの関数 \(q(t)\) で決定されるとする．\(q(t)\) が丁度 \(S\) を最小にするような関数であったとする．これは \(q(t)\) の代わりに別の任意関数 \(q(t)+\delta q(t)\) を持って来ると \(S\) が増加してしまうことを意味する．ここで \(\delta q(t)\) は関数 \(q(t)\) の「変分」といい, \(t_1\) から \(t_2\) までの時間全体に渡って小さな関数であり, かつ \(t=t_1\) と \(t=t_2\) ではゼロでなければならない (図 1 を参照)：
\begin{equation}
\delta q(t_1)=\delta q(t_2)=0
\tag{3}
\end{equation}
\delta q(t_1)=\delta q(t_2)=0
\tag{3}
\end{equation}
図 1. 任意関数 \(q’_i(t)=q_i(t)+\delta q_i(t)\) の取り方
最小作用の原理は「\(q\) を \(q+\delta q\) に変えたとき, \(S\) の変分 \(\delta S\) がゼロになること」である：
\begin{align}
\delta S &=\int_{t_{1}}^{t_{2}} L(q+\delta q,\dot{q}+\delta\dot{q},t)\,dt\ – \int_{t_{1}}^{t_{2}} L(q,\dot{q},t)\,dt\\
&=\int_{t_{1}}^{t_{2}} \big\{ L(q+\delta q,\dot{q}+\delta\dot{q},t)-L(q,\dot{q},t)\big\}\,dt\\
&=\int_{t_{1}}^{t_{2}} \delta L(q,\dot{q},t)\,dt
=\int_{t_{1}}^{t_{2}} \left(\ppdiff{L}{q}\delta q + \ppdiff{L}{\dot{q}}\delta \dot{q}\right)\,dt\\
&=\int_{t_{1}}^{t_{2}} \ppdiff{L}{q}\delta q\,dt + \int_{t_{1}}^{t_{2}} \ppdiff{L}{\dot{q}}\delta \dot{q}\,dt=0
\tag{4}
\end{align}
\delta S &=\int_{t_{1}}^{t_{2}} L(q+\delta q,\dot{q}+\delta\dot{q},t)\,dt\ – \int_{t_{1}}^{t_{2}} L(q,\dot{q},t)\,dt\\
&=\int_{t_{1}}^{t_{2}} \big\{ L(q+\delta q,\dot{q}+\delta\dot{q},t)-L(q,\dot{q},t)\big\}\,dt\\
&=\int_{t_{1}}^{t_{2}} \delta L(q,\dot{q},t)\,dt
=\int_{t_{1}}^{t_{2}} \left(\ppdiff{L}{q}\delta q + \ppdiff{L}{\dot{q}}\delta \dot{q}\right)\,dt\\
&=\int_{t_{1}}^{t_{2}} \ppdiff{L}{q}\delta q\,dt + \int_{t_{1}}^{t_{2}} \ppdiff{L}{\dot{q}}\delta \dot{q}\,dt=0
\tag{4}
\end{align}
ここで第2項目を部分積分する．すると \(\displaystyle{\delta \dot{q}=\frac{d\delta q}{dt}}\) であることから,
\begin{equation}
\int_{t_{1}}^{t_{2}}\ppdiff{L}{\dot{q}}\delta \dot{q}\,dt=\int_{t_{1}}^{t_{2}}\ppdiff{L}{\dot{q}}\frac{d\delta q}{dt}\,dt
=\left[\ppdiff{L}{\dot{q}}\delta q\right]_{t_1}^{t_2} -\int_{t_1}^{t_2} \frac{d}{dt}\left(\ppdiff{L}{\dot{q}}\right)\delta q\,dt
\tag{5}
\end{equation}
\int_{t_{1}}^{t_{2}}\ppdiff{L}{\dot{q}}\delta \dot{q}\,dt=\int_{t_{1}}^{t_{2}}\ppdiff{L}{\dot{q}}\frac{d\delta q}{dt}\,dt
=\left[\ppdiff{L}{\dot{q}}\delta q\right]_{t_1}^{t_2} -\int_{t_1}^{t_2} \frac{d}{dt}\left(\ppdiff{L}{\dot{q}}\right)\delta q\,dt
\tag{5}
\end{equation}
このとき, 条件式 (3) から第1項目はゼロとなることに注意する．よって, 式 (4) の \(\delta S\) は,
\begin{equation}
\delta S =\int_{t_{1}}^{t_{2}} \ppdiff{L}{q}\delta q\,dt -\int_{t_1}^{t_2} \frac{d}{dt}\left(\ppdiff{L}{\dot{q}}\right)\delta q\,dt
= \int_{t_1}^{t_2} \left(\ppdiff{L}{q}-\frac{d}{dt}\ppdiff{L}{\dot{q}}\right)\delta q(t)\,dt=0
\tag{5}
\end{equation}
\delta S =\int_{t_{1}}^{t_{2}} \ppdiff{L}{q}\delta q\,dt -\int_{t_1}^{t_2} \frac{d}{dt}\left(\ppdiff{L}{\dot{q}}\right)\delta q\,dt
= \int_{t_1}^{t_2} \left(\ppdiff{L}{q}-\frac{d}{dt}\ppdiff{L}{\dot{q}}\right)\delta q(t)\,dt=0
\tag{5}
\end{equation}
この残った項では「\(\delta q(t)\) が任意に選べ, その積分がゼロとなる」ことになる．それが可能なのは, 括弧内の量が常にゼロであるときだけである．よって,
\begin{equation}
\ppdiff{L}{q}-\frac{d}{dt}\ppdiff{L}{\dot{q}}=0,\quad \mr{or}\quad \frac{d}{dt}\ppdiff{L}{\dot{q}}-\ppdiff{L}{q}=0
\tag{6}
\end{equation}
\ppdiff{L}{q}-\frac{d}{dt}\ppdiff{L}{\dot{q}}=0,\quad \mr{or}\quad \frac{d}{dt}\ppdiff{L}{\dot{q}}-\ppdiff{L}{q}=0
\tag{6}
\end{equation}
自由度が1以上の場合には, 最小作用の原理に於いて, \(s\) 個の関数 \(q_i(t)\) を独立に変えなければならない．このとき \(s\) 個の方程式を得ることは明らかである：
\begin{equation}
\frac{d}{dt}\ppdiff{L}{\dot{q}_i}-\ppdiff{L}{q_i}=0\qquad \big( i= 1,2,\dotsb, s \big)
\tag{7}
\end{equation}
\frac{d}{dt}\ppdiff{L}{\dot{q}_i}-\ppdiff{L}{q_i}=0\qquad \big( i= 1,2,\dotsb, s \big)
\tag{7}
\end{equation}
これが求める微分方程式であって「ラグランジュ方程式」または「オイラーの方程式」と呼ばれている．
ラグランジアンの決定には, 座標と時間の任意関数 \(f(q,t)\) の時間についての完全導関数を付け加えてもよいという任意性が残る：
\begin{equation}
L'(q,\dot{q},t)=L(q,\dot{q},t)+\frac{d}{dt}f(q,t)
\tag{8}
\end{equation}
L'(q,\dot{q},t)=L(q,\dot{q},t)+\frac{d}{dt}f(q,t)
\tag{8}
\end{equation}
場の中の電荷
場の4元ポテンシャル
与えられた電磁場の中で運動する粒子に対する作用は二つの部分から, すなわち, 自由粒子の作用 \(S_{1}\) と, 粒子と場との相互作用を記述する項 \(S_{int}\) とからなる．後者は, 粒子を特徴付ける量と, 場を特徴付ける量との両方を含むはずである．場の性質は「4元ポテンシャル」と呼ばれる4元ベクトル \(A_{\mu}=(\phi,\mb{A})\) によって特徴付けられる．その成分は座標と時間の関数である．これらは次の形で作用の中に現れる：
\begin{equation}
S_{int}=-\frac{e}{c}\int_{a}^{b} A_{\mu}\,dx^{\mu}=-\frac{e}{c}\int_{a}^{b} \big(\phi,-\mb{A}\big)\big(cdt,d\mb{r}\big)
=-\frac{e}{c}\int_{a}^{b} \big(\phi cdt-\mb{A}\cdot d\mb{r}\big)
\tag{9}
\end{equation}
S_{int}=-\frac{e}{c}\int_{a}^{b} A_{\mu}\,dx^{\mu}=-\frac{e}{c}\int_{a}^{b} \big(\phi,-\mb{A}\big)\big(cdt,d\mb{r}\big)
=-\frac{e}{c}\int_{a}^{b} \big(\phi cdt-\mb{A}\cdot d\mb{r}\big)
\tag{9}
\end{equation}
ただし \(A_{\mu}\) は, 粒子の世界線上の点に於けるものであり, 乗数 \(1/c\) は便宜のために導入してある．従って, 電磁場の中の粒子に対する作用関数の形は次のようになる：
\begin{align}
S&=S_{1}+S_{int}=-mc\int_{a}^{b} ds -\frac{e}{c}\int_{a}^{b} A_{\mu}\,dx^{\mu}\\
&=\int_{a}^{b}\left(-mc\,ds+\frac{e}{c}\mb{A}\cdot d\mb{r}-e\phi\,dt\right)
\tag{10}
\end{align}
S&=S_{1}+S_{int}=-mc\int_{a}^{b} ds -\frac{e}{c}\int_{a}^{b} A_{\mu}\,dx^{\mu}\\
&=\int_{a}^{b}\left(-mc\,ds+\frac{e}{c}\mb{A}\cdot d\mb{r}-e\phi\,dt\right)
\tag{10}
\end{align}
あるいは, 粒子の速度 \(\mb{v}=d\mb{r}/dt\) を導入して時間についての積分にすると, 世界間隔は固有時を \(d\tau\) そして \(\beta=v/c\) とすれば \(ds=cd\tau=cdt\sqrt{1-\beta^{2}}\) であるから次となる：
\begin{equation}
S = \int_{a}^{b}\left(-mc^{2}\sqrt{1-\frac{v^{2}}{c^{2}}} +\frac{e}{c}\mb{A}\cdot\mb{v}-e\phi\right)\,dt
\equiv \int_{a}^{b}L\,dt
\tag{11}
\end{equation}
S = \int_{a}^{b}\left(-mc^{2}\sqrt{1-\frac{v^{2}}{c^{2}}} +\frac{e}{c}\mb{A}\cdot\mb{v}-e\phi\right)\,dt
\equiv \int_{a}^{b}L\,dt
\tag{11}
\end{equation}
よって, 電磁場の中の電荷のラグランジアン \(L\) は次である：
\begin{equation}
L = -mc^{2}\sqrt{1-\frac{v^{2}}{c^{2}}} + \frac{e}{c}\mb{A}\cdot\mb{v} – e\phi
\tag{12}
\end{equation}
L = -mc^{2}\sqrt{1-\frac{v^{2}}{c^{2}}} + \frac{e}{c}\mb{A}\cdot\mb{v} – e\phi
\tag{12}
\end{equation}
このラグランジアンは自由粒子のそれと \((e/c)\mb{A}\cdot\mb{v}-e\phi\) だけ異なっているから, この項が電荷と場の相互作用を表わしていることになる．
一般化運動量 \(\mb{P}\) は導関数 \(\partial L/\partial\dot{\mb{r}}\) であった． よって,
\begin{equation}
\mb{P}=\ppdiff{L}{\mb{v}}=\frac{m\mb{v}}{\ds{\sqrt{1-\frac{v^{2}}{c^{2}}}}}+\frac{e}{c}\mb{A}=\mb{p}+\frac{e}{c}\mb{A}
\tag{13}
\end{equation}
\mb{P}=\ppdiff{L}{\mb{v}}=\frac{m\mb{v}}{\ds{\sqrt{1-\frac{v^{2}}{c^{2}}}}}+\frac{e}{c}\mb{A}=\mb{p}+\frac{e}{c}\mb{A}
\tag{13}
\end{equation}
ただし \(\mb{p}\) は通常の運動量であり, 単に「運動量」と言えばこれのことを指すものとする．
場の中の電荷の運動方程式
場の中に置かれた電荷は, 場からの力を受けるだけでなく, 反対に場に対しても作用を及ぼし, 場を変化させる．けれども, 電荷 \(e\) が大きくなければ, 場に対する電荷の作用, すなわち, 電荷による場の変化は無視することが出来る (電荷をこの意味で小さいと見做して良い条件は, その運動によって生じるいわゆる放射減衰力が小さいことである)．この場合には, 与えられた場の中の電荷の運動を考察する際に, 場自体は電荷の座標や速度には依らないと仮定してよい．
与えられた電磁場の中の電荷の運動方程式は, 式 (6) のラグランジュ方程式から見出される：
\begin{equation}
\frac{d}{dt}\ppdiff{L}{\mb{v}}=\ppdiff{L}{\mb{r}}
\tag{14}
\end{equation}
\frac{d}{dt}\ppdiff{L}{\mb{v}}=\ppdiff{L}{\mb{r}}
\tag{14}
\end{equation}
このとき, 導関数 \(\partial L/\partial \mb{v}\) は式 (13) の一般化運動量である．また, \(L\) は前式 (12) であるから,
\begin{equation}
\ppdiff{L}{\mb{r}}\equiv \nabla L =\frac{e}{c}\nabla\,(\mb{A}\cdot\mb{v})\, – \,e\nabla\,\phi
\tag{15}
\end{equation}
\ppdiff{L}{\mb{r}}\equiv \nabla L =\frac{e}{c}\nabla\,(\mb{A}\cdot\mb{v})\, – \,e\nabla\,\phi
\tag{15}
\end{equation}
ここで次のベクトル解析の公式を利用する：
\begin{equation}
\nabla(\mb{a}\cdot\mb{b})=\mb{a}\cdot(\nabla\,\mb{b})+\mb{b}\cdot(\nabla\,\mb{a})+\mb{b}\times(\nabla\times\mb{a})
+\mb{a}\times(\nabla\times\mb{b})
\tag{16}
\end{equation}
\nabla(\mb{a}\cdot\mb{b})=\mb{a}\cdot(\nabla\,\mb{b})+\mb{b}\cdot(\nabla\,\mb{a})+\mb{b}\times(\nabla\times\mb{a})
+\mb{a}\times(\nabla\times\mb{b})
\tag{16}
\end{equation}
この公式を式 (15) の \(\mb{A}\cdot\mb{v}\) に適用し,「速度 \(\mb{v}=\dot{\mb{r}}\) は定数」と見做すならば \(\nabla\mb{v}=0\), \(\nabla\times\mb{v}=0\) となることに注意すると,
\begin{align}
\nabla\,(\mb{A}\cdot\mb{v})&=\mb{A}\cdot(\nabla\mb{v})+\mb{v}\cdot(\nabla \mb{A})+\mb{v}\times(\nabla\times\mb{A})
+\mb{A}\times(\nabla\times\mb{v})\\
&=\mb{v}\cdot(\nabla \mb{A})+\mb{v}\times(\nabla\times\mb{A})
=\mb{v}\cdot(\nabla \mb{A})+\mb{v}\times\mr{rot}\,\mb{A}
\tag{17}
\end{align}
\nabla\,(\mb{A}\cdot\mb{v})&=\mb{A}\cdot(\nabla\mb{v})+\mb{v}\cdot(\nabla \mb{A})+\mb{v}\times(\nabla\times\mb{A})
+\mb{A}\times(\nabla\times\mb{v})\\
&=\mb{v}\cdot(\nabla \mb{A})+\mb{v}\times(\nabla\times\mb{A})
=\mb{v}\cdot(\nabla \mb{A})+\mb{v}\times\mr{rot}\,\mb{A}
\tag{17}
\end{align}
従って式 (15) は,
\begin{equation}
\ppdiff{L}{\mb{r}}=\frac{e}{c}\mb{v}\cdot(\nabla\mb{A})+\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A}-e\,\mr{grad}\,\phi
\tag{18}
\end{equation}
\ppdiff{L}{\mb{r}}=\frac{e}{c}\mb{v}\cdot(\nabla\mb{A})+\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A}-e\,\mr{grad}\,\phi
\tag{18}
\end{equation}
よって, 式 (14) のラグランジュ方程式は
\begin{equation}
\frac{d}{dt}\ppdiff{L}{\mb{v}}=\frac{d}{dt}\left(\mb{p}+\frac{e}{c}\mb{A}\right)
=\frac{d\mb{p}}{dt}+\frac{e}{c}\frac{d\mb{A}}{dt}
=\ppdiff{L}{\mb{r}}=\frac{e}{c}\mb{v}\cdot(\nabla\mb{A})+\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A} -e\,\mr{grad}\,\phi
\tag{19}
\end{equation}
\frac{d}{dt}\ppdiff{L}{\mb{v}}=\frac{d}{dt}\left(\mb{p}+\frac{e}{c}\mb{A}\right)
=\frac{d\mb{p}}{dt}+\frac{e}{c}\frac{d\mb{A}}{dt}
=\ppdiff{L}{\mb{r}}=\frac{e}{c}\mb{v}\cdot(\nabla\mb{A})+\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A} -e\,\mr{grad}\,\phi
\tag{19}
\end{equation}
さらにこの式 (19) 中のベクトルポテンシャル \(\mb{A}\) の微分 \(d\mb{A}\) は, 時間的変化と空間的変化の２つから成るから,
\begin{equation}
d\mb{A}=\ppdiff{\mb{A}}{t}dt+\ppdiff{\mb{A}}{\mb{r}}\cdot d\mb{r}
=\ppdiff{\mb{A}}{t}dt+(\nabla\mb{A})\cdot d\mb{r}
\end{equation}
d\mb{A}=\ppdiff{\mb{A}}{t}dt+\ppdiff{\mb{A}}{\mb{r}}\cdot d\mb{r}
=\ppdiff{\mb{A}}{t}dt+(\nabla\mb{A})\cdot d\mb{r}
\end{equation}
すると \(\mb{v}=d\mb{r}/dt\) より,
\begin{equation}
\frac{d\mb{A}}{dt}=\ppdiff{\mb{A}}{t}+(\nabla\mb{A})\cdot\frac{d\mb{r}}{dt}
=\ppdiff{\mb{A}}{t}+\mb{v}\cdot(\nabla\mb{A})
\tag{20}
\end{equation}
\frac{d\mb{A}}{dt}=\ppdiff{\mb{A}}{t}+(\nabla\mb{A})\cdot\frac{d\mb{r}}{dt}
=\ppdiff{\mb{A}}{t}+\mb{v}\cdot(\nabla\mb{A})
\tag{20}
\end{equation}
これを式 (19) 中の \(d\mb{A}/dt\) に用いて整理すれば, 次のような「電磁場中の粒子の運動方程式」が得られる：
\begin{equation}
\frac{d\mb{p}}{dt}=-\frac{e}{c}\ppdiff{\mb{A}}{t}-e\,\rm{grad}\,\phi +\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A}
=e\left(-\frac{1}{c}\ppdiff{\mb{A}}{t}-\mr{grad}\,\phi\right)+\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A}
\tag{21}
\end{equation}
\frac{d\mb{p}}{dt}=-\frac{e}{c}\ppdiff{\mb{A}}{t}-e\,\rm{grad}\,\phi +\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A}
=e\left(-\frac{1}{c}\ppdiff{\mb{A}}{t}-\mr{grad}\,\phi\right)+\frac{e}{c}\mb{v}\times\mr{rot}\,\mb{A}
\tag{21}
\end{equation}
この右辺は, 電磁場の中の電荷に働く力に相当するはずで, それは粒子の速度に依らない部分と粒子速度に依存する最終項とから成る．それは速度に比例し速度に直交している．更に, 次の「電場の強さ \(\mb{E}\)」と「磁場の強さ \(\mb{H}\)」とを用いる：
\begin{equation}
\mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t}-\mr{grad}\,\phi,\quad
\mb{H}=\mr{rot}\,\mb{A}=\nabla\times\mb{A}
\tag{22}
\end{equation}
\mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t}-\mr{grad}\,\phi,\quad
\mb{H}=\mr{rot}\,\mb{A}=\nabla\times\mb{A}
\tag{22}
\end{equation}
すると,式 (21) は最終的に次のような「電荷の運動方程式」の形に書くことが出来る：
\begin{equation}
\frac{d\mb{p}}{dt}=e\,\mb{E}+\frac{e}{c}\mb{v}\times\mb{H}
\tag{23}
\end{equation}
\frac{d\mb{p}}{dt}=e\,\mb{E}+\frac{e}{c}\mb{v}\times\mb{H}
\tag{23}
\end{equation}
この右辺の表現は, まさに前のブログに記した「ローレンツ力」になっている．速度が光速度に比べて小さいときは, 運動量 \(\mb{p}\) は近似的に古典論の表現 \(m\mb{v}\) に等しく, 運動方程式 (23) は次となる：
\begin{equation}
m\frac{d\mb{v}}{dt} = e\,\mb{E}+\frac{e}{c}\mb{v}\times\mb{H}
\tag{24}
\end{equation}
m\frac{d\mb{v}}{dt} = e\,\mb{E}+\frac{e}{c}\mb{v}\times\mb{H}
\tag{24}
\end{equation}
以上のようにして, ラグランジアン \(L\) から前のブログ記事と同じ「電荷の運動方程式」を得ることが出来た．
上記の導出手順をちょっと眺めただけであると, 如何にも運動方程式はラグランジュ方程式から自動的に導出されたように思える．しかしこの場合,「ラグランジアン \(L\) は式 (12) で最初に与えた」ことに注意しなければならない．その式 (12) のラグランジアンは, 式(9)と式(10)から適当に作られたものだ．このように, ラグランジュ方程式から運動方程式を得るには, まず「ラグランジアン \(L\) を適当に選定する必要がある」ことに注意しなければならない．「運動方程式に対するラグランジアンを得るには色々と推論する他なく, 一定の方法というのはない」(高橋康：「解析力学入門」より) のである．
