はてなブログ：「ファインマンさんの肩に乗って晴耕雨読の日々」に書いていた記事を今日から順にこちらに移していこう．先ずはファインマン経路積分の第6章の問題をまとめて移してしまう．
\(\)
Problem 6-1
Suppose the potential can be written as \(U+V\), where \(V\) is small but \(U\) is large. Suppose further that the kernel for motion in the potential of \(U\) alone can be worked out ( for example, \(U\) might be quadratic in \(x\) and independent of time ). Show that the motion in the complete potential \(U+V\) is described by Eqs. (6-4), (6-11), (6-13), and (6-14) with \(K_0\) replaced by \(K_{U}\), where \(K_{U}\) is the kernel for motion in the potential \(U\) alone. Thus we can consider \(V\) as a perturbation on the potential \(U\). We can say that \((-i/\hbar)V\) is the amplitude to be scattered by the perturbing part of the potential ( per unit volume and per unit time ). \(K_{U}\) is the amplitude for the motion in the system in the unperturbed potential \(U\).
この場合, 式 (6.1) に相当する式は次となる：
K_{U+V}(b,a)&=\int_{a}^{b}\mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\left\{\frac{m}{2}\dot{x}^{2}-U(x,t)-V(x,t)\right\}\right]\notag\\
&=\int_{a}^{b}\mathscr{D}x(t)\,\exp\left[\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\left\{\frac{m}{2}\dot{x}^{2}-U(x,t)\right\}\right]\exp\left[-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,t)\right]
\tag{1}
\end{align}
今度は, ポテンシャル \(U+V\) の内の \(V\) だけを「ポテンシャルの小さい部分」とすることで, やはり式 (6.3) と同様な級数展開が出来る：
\exp\left[-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,t)\right]=1-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,t)
+\frac{1}{2!}\left(\frac{i}{\hbar}\right)^{2}\left[\int_{t_a}^{t_b}dt\,V(x,t)\right]^{2}+\dotsb
\tag{2}
\end{align}
これを式 (1) に代入すれば, 式 (6.4) に相当する式として次が得られる：
K_{U+V}(b,a)&=\int_{a}^{b}\mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,
\left[\frac{m}{2}\dot{x}^{2}-U(x,t)\right]\right\}\\
&\qquad\times\Bigg[1-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,t)
+\frac{1}{2!}\left(\frac{i}{\hbar}\right)^{2}\left[\int_{t_a}^{t_b}dt\,V(x,t)\right]^{2}+\dotsb\Bigg]\\
&=K_{U}(b,a)+K^{(1)}(b,a)+K^{(2)}(b,a)+\dotsb
\tag{3}
\end{align}
ただし式 (6.5) の \(K_0(b,a)\) に相当するのは, 次の \(K_U(b,a)\) となる：
K_{U}(b,a)=\int_{a}^{b}\mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\left[\frac{m}{2}\dot{x}^{2}-U(x,t)\right]\right\}
\tag{4}
\end{equation}
また \(K^{(1)}(b,a)\) や \(K^{(2)}(b,a)\) は次となる：
K^{(1)}(b,a)&=-\frac{i}{\hbar}\int_a^{b}\mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt
\,\left[\frac{m\dot{x}^{2}}{2}-U(x,t)\right]\right\}\int_{t_a}^{t_b}ds\,V\bigl[x(s),s\bigr],
\tag{5}\\
K^{(2)}(b,a)&=-\frac{1}{2\hbar^{2}}\int_a^{b}\mathscr{D}x(t)\,\exp\left\{\frac{i}{\hbar}
\int_{t_a}^{t_b}dt\,\left[\frac{m\dot{x}^{2}}{2}-U(x,t)\right]\right\}\\
&\qquad\qquad\times\int_{t_a}^{t_b}ds\,V\bigl[x(s),s\bigr]\int_{t_a}^{t_b}ds^{‘}\,V\bigl[x(s^{‘}),s^{‘}\bigr]
\tag{6}
\end{align}
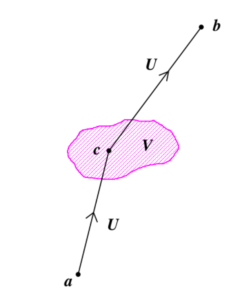
そしてポテンシャル \(U+V\) による散乱を, 摂動ポテンシャル \(V\) による散乱と解釈するには, 式 (6.12) における自由粒子核 \(K_0(b,a)\) を, ポテンシャル \(U\) の下での粒子核 \(K_{U}(b,a)\) で置き換えればよい：
K_{U} (b,c)\,\left[-\frac{i}{\hbar}V(c)\,dx_c\,dt_c\right]\,K_{U}(c,a)
\tag{7}
\end{equation}
ただし \(V(c)\) は点 \(c\) におけるポテンシャルの摂動部分である (下図を参照)．よって, 式 (6.11) や 式 (6.13), 式 (6.14) に相当する式は次となる：
K_{U+V}(b,a)&=K_U(b,a)+K^{(1)}(b,a)+K^{(2)}(b,a)+\dotsb,\tag{8}\\
K^{(1)}(b,a)&=-\frac{i}{\hbar}\int_{t_a}^{t_b}dt_c\int_{-\infty}^{\infty}dx_c\,K_U(b,c)\,V(c)\,K_U(c,a),\tag{9}\\
K^{(2)}(b,a)&=\left(-\frac{i}{\hbar}\right)^{2}\int d\tau_c\int d\tau_d\,K_U(b,c)\,V(c)\,K_U(c,d)\,V(d)\,K_U(d,a),\tag{10}\\
K^{(i)}(b,a)&=0,\quad (\,t_b < t_a\,),\quad i=1,2,3,\dotsb \label{11} \end{align}
図 1. この場合には, 自由粒子でなく, ポテンシャル \(U\) の下で運動している粒子が, 点 \(c\) で小さなポテンシャル \(V\) による散乱を受け, その後また同様にポテンシャル \(U\) の下で運動して行くと考える．
