\(\)
Problem 6-9
Suppose we introduce the fact that the atomic nucleus has a finite radius given by
\def\mr#1{\mathrm{#1}}
r=1.2\times 10^{-13}\times (\mr{mass}\ \mr{number})^{1/3} \,\mr{cm}
\tag{6-56}
\end{equation}
and assume that the nuclear charge is distributed approximately uniformly in a sphere of this radius. What is the effect of this assumption on the cross section for the scattering of electrons by atoms at large values of the momentum transfer \(q\) ?
Show how the nuclear radius can be determined along with some of the details of the nuclear charge distribution by making use of this effect. How large must the momentum \(p\) of the incoming electrons be in order to produce an appreciable effect? Would one observe more carefully the large or small scattering angles? Why?
Note : In this type of experiment the required electron momentum is so high that actually the relativistic formula \(E=\sqrt{m^{2}c^{4}+c^{2}p^{2}}-mc^{2}\) must be used to find the kinetic energy. So, strictly, we should not be allowed to use non relativistic formulas to describe the interaction. However, the relations between momentum and wavelength and between energy and frequency are not changed in the relativistic region. Since it is the wavelength which determines the resolving power of this “electron microscope” , the momentum calcuculated by non relativistic formulas is still correct.
( 解答 ) 関数 \(v(q)\) は前のブログ記事の式(6-50′) に於いて, 原子内電子の遮蔽効果を無視し「核の電荷分布関数 \(\rho_n(\mathbf{r})\)」だけを考えることで得ることが出来ることに注意する ( その根拠はこの記事の最後の方に記してある )：
\def\mb#1{\mathbf{#1}}
F(q)&\equiv\int d^{3}\mb{r}\,e^{i\mb{q}\cdot\mb{r}/\hbar}\,\rho_n(\mb{r}),\\
\rightarrow &\quad v(\mb{q})=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}F(q)
\tag{1}
\end{align}
このときの核電荷分布関数 \(\rho\_n(r)\) の「規格化条件」は次である：
\int \rho_n(\mb{r})\,d^{3}\mb{r}=1
\end{equation}
従って,
\int \rho_n(\mb{r})\,d^{3}\mb{r}&=4\pi\int_0^{\infty}\rho_n(r)r^{2}\,dr=4\pi\rho_0\int_0^{r_n}r^{2}\,dr\\
&=\frac{4}{3}\pi r_n^{3}\,\rho_0=1,\quad \rightarrow\quad \rho_0=\frac{3}{4\pi r_n^{3}}
\tag{2}
\end{align}
式 (1) から「形状因子 \(F(q)\) は, 核電荷分布関数 \(\rho\_n(\mb{r})\) をフーリエ変換したものに相当している」ことが分かる．球対称である場合, 核電荷分布関数 \(\rho\_n(\mb{r})\) は半径 \(r\) にのみに依存する．形状因子 \(F(q)\) の角度積分だけを積分(全立体角で積分)すると,
F(q)&=\int e^{i\mb{q}\cdot\mb{r}/\hbar}\,\rho(\mb{r})\,d^{3}\mb{r}
=\iiint e^{iqr\cos\theta/\hbar}\rho(r)\,r^{2}dr\sin\theta\,d\theta\,d\phi\\
&=\int_0^{2\pi}d\phi\int_0^{\infty}r^{2}dr\,\rho(r)
\int_0^{\pi}d\theta\,e^{iqr\cos\theta/\hbar}\sin\theta
\tag{3}
\end{align}
ここで \(t=\cos\theta\) とすると次となる：
F(q)&=2\pi\int_0^{\infty}r^{2}dr\,\rho(r)\int_{-1}^{1}e^{i q r t/\hbar}\,dt\\
&=2\pi\int_0^{\infty}r^{2}dr\,\rho(r)\frac{2\hbar}{q r}\sin\left(\frac{q r}{\hbar}\right)\\
&=4\pi\int_0^{\infty}\rho(r)\frac{\sin q r/\hbar}{q r/\hbar}r^{2}\,dr \\
&=\frac{4\pi\hbar}{q}\int_0^{\infty}r\,\rho(r)\sin\left(\frac{q}{\hbar}r\right)\,dr
\tag{4}
\end{align}
この場合電荷密度は一定： \(\rho(r)=\rho_0\) なので, 積分の外に出すことが出来る．前のブログ記事に示した公式
I_1=\int_0^{a}x\sin k x\,dx=\frac{1}{k^{2}}\big(\sin k a -k a\cos k a\big)
\end{equation}
及び, 式 (2) より得られる \(\rho_0=3/4\pi r_n^{3}\) も利用すると「電子散乱の形状因子 \(F(q)\)」は次となる：
F(q)&=4\pi\rho_0\int_0^{\infty}\frac{\sin q r/\hbar}{q r/\hbar}r^{2}\,dr
=\frac{4\pi\hbar\,\rho_0}{q}\int_0^{r_n}r\,\sin\left(\frac{q}{\hbar}r\right)\,dr\\
&=\frac{4\pi\hbar}{q}\cdot\frac{3}{4\pi r_n^{3}}\cdot\frac{\hbar^{2}}{q^{2}}\left\{\sin\left(\frac{r_n}{\hbar}q\right)
-\left(\frac{r_n}{\hbar}q\right)\cos\left(\frac{r_n}{\hbar}q\right)\right\}\\
&=3\left(\frac{r_n}{\hbar}q\right)^{-3}\left\{\sin\left(\frac{r_n}{\hbar}q\right)
-\left(\frac{r_n}{\hbar}q\right)\cos\left(\frac{r_n}{\hbar}q\right)\right\}
\tag{5}
\end{align}
この形状因子 \(F(q)\) は \(\alpha=q r_n/\hbar\equiv aq,\ a=r_n/\hbar\) とすると次のように表せる：
F(q)=\frac{3}{\alpha^{3}}\left(\sin\alpha -\alpha\cos\alpha\right)
\tag{6}
\end{equation}
この \(F(q)\) と \(|F(q)|^{2}\) のグラフの概形は前のブログ記事に示してある．
関数 \(v(q)\) は, 式 (1) と式 (5) とから次となる：
v(q)&=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}F(q)\\
&=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}\frac{3}{(q r_n/\hbar)^{3}} \left\{\sin\left(\frac{r_n}{\hbar}q\right)
-\left(\frac{r_n}{\hbar}q\right)\cos\left(\frac{r_n}{\hbar}q\right)\right\}
\tag{7}
\end{align}
運動量移行 \(q\) と散乱角度 \(\theta\) との関係は, 問題 6-6 中の式 (6-47) で与えられている：
q=2p\sin\frac{\theta}{2}
\tag{6-47′}
\end{equation}
従って, 小さな \(q\) は小さな振れか小さな運動量(遅い電子)かに対応する．このどちらの場合でも遮蔽されたクーロン力場による散乱のときと同様に, 運動量移行 \(q\) が小さい場合 (波長が原子核の拡がり \(r_n\) よりもずっと大きい場合), 式 (11) の \(\alpha=r_n q/\hbar\) は非常に小さくなる．よって,「原子核半径 \(r_n\) に関する情報は, 形状因子の極小値の位置だけでなくて, 形状因子の \(q^{2}\to 0\) での振舞いを調べることでも得ることが出来る」と言える ( 以下は B. Povh に依る)．運動量移行 \(q\) が小さい場合には, 式 (1) の \(F(q)\) は \(q\) で冪級数展開できる：
F(q)&=\int d^{3}\mb{r}\,\rho_n(\mb{r})\,e^{i\mb{q}\cdot\mb{r}/\hbar}
=\int d^{3}\mb{r}\,\rho_n(\mb{r})\sum_{n=0}^{\infty}\frac{1}{n!}
\left(\frac{i q r\cos\theta}{\hbar}\right)^{n}\\
&=\int_0^{2\pi}d\phi \int_0^{\infty} r^{2}\,dr\int_{-1}^{1}d(\cos\theta)\,\left[1+\frac{i q r\cos\theta}{\hbar}-\frac{1}{2!}
\left(\frac{q r\cos\theta}{\hbar}\right)^{2}+\dotsb\right]\rho_n(\mb{r})\\
&\equiv F(0)+F^{‘}(0)q+\frac{F^{”}(0)}{2}q^{2}+\dotsb
\tag{8}
\end{align}
このとき, 変数変換 \(t=\cos\theta\) としたときの \(dt=d(\cos\theta)\) 積分の積分範囲は \([-1,1]\) となる．このことから \(\cos\theta\) が奇数乗のべきはゼロになってしまうことに注意する．よって，
F(q)=4\pi\int_0^{\infty}\rho(r)r^{2}\,dr-\frac{1}{6}\frac{q^{2}}{\hbar^{2}}4\pi \int_0^{\infty}\rho(r)r^{4}\,dr+\dotsb
\tag{9}
\end{equation}
このため, 以降では形状因子は \(F(\mb{q}^{2})\) と表現することにする．
式 (6-50’) 下の核の電荷分布関数 \(\rho_n(\mb{r})\) の「規格化」より第 1 項は \(1\) である．また更には, 電荷の「平均二乗半径」(mean square radius) を次式で定義する：
\left\langle r^{2}\right\rangle \equiv 4\pi\int_0^{\infty}r^{2}\,\rho_n(r)\,dr
\tag{10}
\end{equation}
すると, 式 (8) は次のように書くことが出来る：
F(q^{2})=F(0)+\frac{F^{”}(0)}{2}q^{2}+\dotsb =1-\frac{1}{6}\frac{q^{2}}{\hbar^{2}}\left\langle r^{2}\right\rangle+\dotsb
\tag{11}
\end{equation}
また, 核電荷分布関数として \(\rho_n(r)=3/4\pi r_n^{3}\) を用いると, 平均二乗半径 \(\left\langle r^{2}\right\rangle\) は核半径 \(r_n\) と次のような関係となることに注意する：
\left\langle r^{2}\right\rangle&=4\pi\int_0^{\infty}r^{2}\,\rho_n(r)\,dr
=4\pi\int_0^{r_n} r^{2}\frac{3}{4\pi r_n^{3}}\,r^{2}\,dr =\frac{3}{r_n^{3}}\int_0^{r_n}r^{4}\,dr =\frac{3}{5}r_n^{2}\\
&\mr{therefore}\quad r_n^{2}=\frac{5}{3} \left\langle r^{2}\right\rangle
\tag{12}
\end{align}
式 (11) から「平均二乗半径 \(\left\langle r^{2}\right\rangle\) を決めるには, 形状因子 \(F(\mb{q}^{2})\) を \(q\) を非常に小さな値まで測定する \([q^{2}\to0]\) ことが必要」と言える．その場合, 式 (16) の両辺を \(q^{2}\) で微分すると,
\frac{d F(q^{2})}{d q^{2}}\simeq -\frac{1}{6\hbar^{2}} \left\langle r^{2}\right\rangle
\tag{13}
\end{equation}
よって \(q^{2}\to 0\) として, 次式を用いることが出来る：
\left\langle r^{2}\right\rangle \simeq \left. -6\hbar^{2}\frac{dF(q^{2})}{d q^{2}}\right|_{q^{2}=0}
\quad\mr{or,}\quad r_n^{2}\simeq \left.-10\hbar^{2}\frac{dF(q^{2})}{d q^{2}}\right|_{q^{2}=0}
\tag{14}
\end{equation}
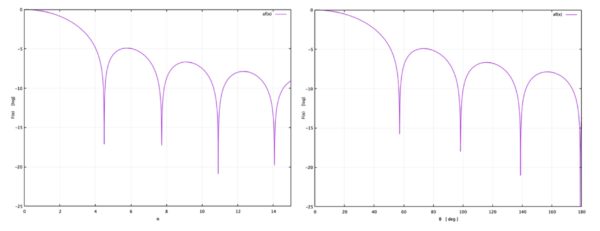
図 1. log スケールに於ける形状因子 \(F(q)\) と散乱角 \(\theta\) との関係． 大きな運動量移行 \(q\) では, 大きな散乱角度にも極小値が出現することが分かる．
次に, 運動量移行 \(q\) が大きい場合を考えてみる．形状因子 \(F(q)\) を更に詳しくプロットしてみると図 1. の右図のようになる．図 1. から, 大きな散乱角度にまで極小値が存在することが分かる．入射電子の運動量 \(p\) が小さい場合には, 式 (8) から「形状因子すなわち微分断面積は角度依存しない」ことが分かる．断面積が目に見えて角度依存し始める運動量は, 上式 (11) で第 1 項と第 2 項とが大体同じ位になる場合として, 次が言えるときであろう：
F(0)\simeq \frac{F^{”}(0)}{2}q^{2} \quad\rightarrow\quad \frac{F^{”}(0)}{F(0)}\frac{q^{2}}{2} \simeq 1
\tag{15}
\end{equation}
大体の場合, これは \(\alpha=r_n q/\hbar\simeq1\) つまり
q\simeq \frac{\hbar}{r_n}\quad \rightarrow\quad q=2p\sin\left(\frac{\theta}{2}\right) \simeq \frac{\hbar}{r_n},
\quad\mr{or,}\quad p\sin\left(\frac{\theta}{2}\right)\simeq\frac{\hbar}{2r_n}
\end{equation}
の場所で起こる．即ち \(\sin(\theta/2)\le 1\) だから, 「散乱断面積の散乱角度に対する顕著な依存性は, 入射電子の運動量 \(p_a\) がおよそ \(p_c=\hbar/2r_n\) 以上になって初めて現れ出すと言えるであろう」．他方, この量 \(p_c\) は『粒子を半径 \(r_n\) 程度の場所に押し込めて置く際に,「不確定性関係」によって要求される程度の運動量である』と言える：
\Delta p\cdot \Delta x =p_c\cdot r_n\simeq \frac{\hbar}{2}\quad \rightarrow\quad p_c\simeq \frac{\hbar}{2r_n}
\tag{16}
\end{equation}
『入射運動量 \(p_a\) が \(p_a r_n\simeq \hbar\) になる位に十分大きいとき, すなわち入射粒子の持つ波長 \(\lambda=h/p_a\) がポテンシャルが大きい領域を通過する際に顕著に振動する程十分に短いとき, 散乱波は角度に依存し始める．換言すれば,「\(p_a r_n\simeq \hbar\) となるまでは, 原子核のポテンシャル井戸の一つの形を別の何らかの形と区別する手段は無い」のである』 (D.Bohmより)．
以下は B.Povh et.al：「素粒子・原子核物理入門」の § 5 を参照して書いている．微分散乱断面積 \(d\sigma/d\Omega\) は式 (6-44) で与えられた：
\frac{d\sigma}{d\Omega}=\left(\frac{m}{2\pi\hbar^{2}}\right)^{2}\left|v(\mb{q})\right|^{2}
\end{equation}
よって,
\frac{d\sigma}{d\Omega}=\left(\frac{m}{2\pi\hbar^{2}}\right)^{2} \left|-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}F(q)\right|^{2}
=\left(\frac{2mZe^{2}}{q^{2}}\right)^{2}\left|F(q)\right|^{2}
\tag{17}
\end{equation}
そこで, 形状因子 \(F(q)\) の絶対値の2乗をプロットしてみると 図 2. のようになる．
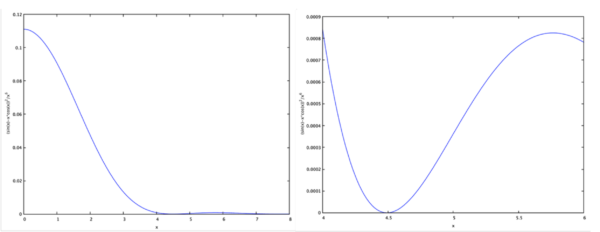
図 2. 左図は式 (6) の形状因子 \(F(q)\) の絶対値の2乗を \(\alpha\) に対して描いたグラフである． 右図は \(\alpha=4\) 付近を拡大したもので, 最初の極小値は \(\alpha=q r_n/\hbar\simeq 4.5\) の位置にあることが分かる．
この図から, 最初の極小値は,
\alpha=\frac{q r_n}{\hbar}\approx 4.5
\tag{18}
\end{equation}
のところに来ることが分かる．従って,「極小値の位置から原子核の拡がり, すなわち核半径を直接に決めることが出来る」と言える．
式 (17) の \(F(q)\) に式 (7) を代入すると次を得る：
\frac{d\sigma}{d\Omega}
=\left(\frac{2mZe^{2}}{q^{2}}\right)^{2} \left|\frac{3}{(qr_n/\hbar)^{3}}\left\{\sin\left(\frac{r_n}{\hbar}q\right)
-\left(\frac{r_n}{\hbar}q\right)\cos\left(\frac{r_n}{\hbar}q\right)\right\}\right|^{2}
\tag{19}
\end{equation}
運動量移行 \(q\) と散乱角度 \(\theta\) の間には式 (6-47) の関係があったから, 散乱角度が小さい場合には次のような近似が可能である：
q=2p\sin\left(\frac{\theta}{2}\right) \quad \rightarrow\quad q\approx 2p \left(\frac{\theta}{2}\right)=p\theta
\tag{20}
\end{equation}
従って, 散乱角が小さい場合では運動量移行 \(q\) は入射電子の運動量 \(p\) と散乱角度にほぼ比例すると言える．形状因子 \(F(q)\) の式 (7) に式 (6-47) の \(q=2p\sin(\theta/2)\) を代入して, 形状因子 \(F(q)\) の散乱角度\(\theta\) への依存の様子をプロットしてみると 図 3. のようになる．この図から,「入射粒子の運動量 \(p\) が大きい場合には, 微分断面積に極小値が出現すること」が分かる．
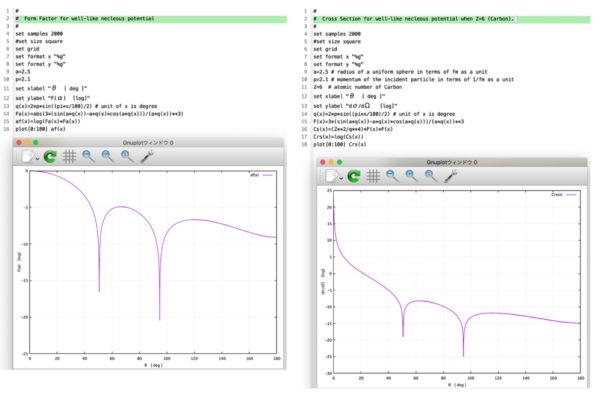
図 3. gnuplot で形状因子 \(F(q)\) と散乱角度 \(\theta\) との関係, 及び炭素原子 \({}^{12}\)C の場合の散乱断面積 \(d\sigma/d\Omega\) と散乱角度 \(\theta\) との関係を描いてみた．縦軸は log スケールである．
例として \({}^{12}\)C の電子散乱の場合, 微分断面積 (従って形状因子) は次の 図 4. のようである．
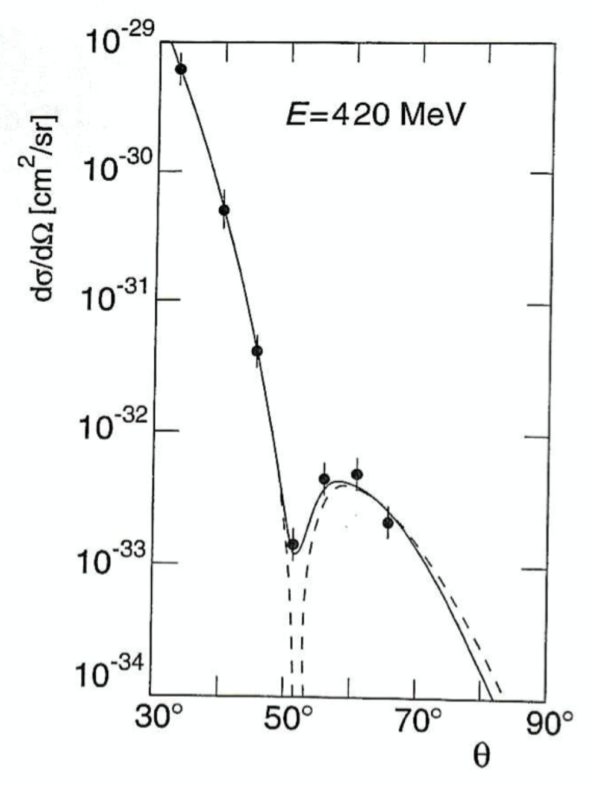
図 4. 電子散乱による \({}^{12}\)C の形状因子の測定．ビームのエネルギーは一定で， \(420\) MeVである． 微分断面積を7つの散乱角度で測定されている．点線はぼけた縁を持つ一様な球により平面波が散乱された場合 (ボルン近似)に相当する．実線は実験データにフィットした厳密な位相差解析を示している．( B. Povh の図 5.5 をコピーしたものである )．
この場合, 極小値の位置は角度 \(51\)° にあることが分かる．これは \(q/\hbar\approx 1.8\,\mr{fm}^{-1}\) に相当する．なぜなら, 原子核・素粒子物理学で使用される単位は次のようである：
1\,&\mr{fm}=10^{-15}\,\mr{m}\ [\mr{Length}],\\
\hbar&=1.0546\times 10^{-34}\,\mr{Js}
=\frac{1.0546\times 10^{-34}\,\mr{Js}}{1.602\times 10^{-19}\mr{J}}\,\mr{eV}\\
&=6.582\times 10^{-22}\,\mr{MeVs}\ [\mr{Angular}\ \mr{Momentum}],\\
\hbar c &=6.582\times 10^{-22}\,\mr{MeVs}\times 3.0\times 10^{8}\,\mr{m}\,\mr{s}^{-1}\\
&= 1.973\times 10^{-13}\,\mr{MeVm}= 197.3\,\mr{MeV}\,\mr{fm}
\end{align}
重要な物理量の次元と質量次元の対応関係は次である( 坂本：「場の量子論」より )：
&[\mr{Momentum}]=[\mr{Energy}]=[\mr{Mass}]=\frac{1}{[\mr{Length}]}=\frac{1}{[\mr{Time}]},\\
&[\mr{Velocity}]=[\mr{Angular Momentum}]=[1]
\end{align}
従って \(\hbar c\) の値から,「\(c=1,\,\hbar=1\) とする自然単位系」では, 次の関係が成り立つと言える：
&\hbar c =1=197.3\,\mr{MeV fm},\ [\mr{Energy}]\times[\mr{Length}]\\
&\rightarrow\quad 197.3\,\mr{MeV}\,[\mr{Energy}]=1\mr{fm}^{-1}\,\frac{1}{[\mr{Length}]}
\end{align}
従って, 電子ビームのエネルギーが \(E=420\) MeVの場合, その運動量は次の量に相当する：
p=\frac{E}{c}=E=420\,\mr{MeV}=\frac{420}{197.3}\mr{fm}^{-1}=2.1\,\mr{fm}^{-1}
\end{equation}
この場合に角度を約 \(\theta=51\)° とすると,
&q=2p\sin\frac{\theta}{2}=2p\sin\left(\frac{51}{180}\pi\right)=2\times 2.1\,\mr{fm}^{-1}
\times 0.43\approx 1.8\,\mr{fm}^{-1},\\
&\rightarrow q/\hbar=1.8\,\mr{fm}^{-1}
\end{align}
となるからである．すると式 (18) より \(r_n\approx 4.5\hbar/q\) であるから, この場合の炭素の原子核半径は, およそ
r_n=\frac{4.5\hbar}{q}=\frac{4.5}{1.8\,\mr{fm}^{-1}}=2.5\,\mr{fm}
\tag{21}
\end{equation}
であると結論することが出来る．因みに, 式 (6-56) から炭素原子 (\(Z=6\), \(A=12\)) の核半径 \(r\) を求めてみると,
r=1.2\times 10^{-13}\times 12^{1/3}\simeq 2.7\times 10^{-13}\,\mathrm{cm}=2.7\,\mathrm{fm}
\end{equation}
となる．
以下は D. ボーム：「量子論」§ 21 からの引用である．
『原子による電子散乱の場合， Born 近似はその妥当性の一般的規準を全く満たしていないにも拘らず, しばしば驚く程よい結果をもたらす．その理由は次の如くである：「原子の端の近くでは Coulomb 的なものとは程遠い．しかし, そこでは核の電荷は殆ど電子によって遮蔽されてしまうため, 非常に弱くなっている．従って, ポテンシャル \(V\) が非常に小さいという単純な理由から, その部分では Born 近似が使える．原子中では, ポテンシャル \(V\) が非常に大きいために Born 近似が破れると期待されるかも知れないが, その辺では遮蔽が無くなって力が Coulomb 的となり, 偶然ながら厳密な結果と Born 近似による結果とが近いものとなる．すなわち, 一般的根拠からでは正当とはなし得ないにも拘らず, 原子全体に亘って Born 近似は相当に良い近似を与えるのである．よって「遮蔽の無い Coulomb 力の場合, Born 近似が当て嵌まるかどうかには無関係に, 散乱断面積は同じものになる』．
そこで, 「原子内電子の遮蔽効果の影響」を式 (6-50′) から考えてみよう：
v(q)&=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}\left[1+\int_{-\infty}^{\infty}\,\rho_n(\mb{r})
e^{i\mb{q}\cdot\mb{r}/\hbar}\,d^{3}\mb{r}-\int \rho_e(\mb{r})\,e^{i\mb{q}
\cdot\mb{r}/\hbar}\,d^{3}\mb{r}\right]
\tag{6-50′}\\
&\equiv v_{Ruth}+v_n(q)+v_e(q),\\
&v_{Ruth}(q)=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}},\qquad
v_n(q)=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}F_n(q),\\
&v_e(q)=\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}\int \rho_e(\mb{r})\,e^{i\mb{q}\cdot\mb{r}/\hbar}\,d^{3}\mb{r}
\end{align}
ただし \(F_n(q)\) は原子核による形状因子で, 今まで \(F(q)\) と記してきたものである．第 3 項目の \(v_e(q)\) が原子内電子の遮蔽効果を与える．その式 (7) に与える影響は, 問題 6-8 の結果から次のように表わすことが出来るであろう：
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
v(q)&=v_{Ruth}(q)+v_n(q)+v_e(q)\\
&=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}\left[1+F_n(q) – \frac{1}{1+\left(\ds{\frac{a}{\hbar}q}\right)^{-2}}\right]
\tag{22}
\end{align}
ただし \(a\) は式 (6-51) で述べられている原子半径 \(a=a_0/Z^{1/3}\) である．その大きさは, 例えば 炭素原子 (\(Z=6\)) を考えるならば,
a=\frac{a_0}{Z^{1/3}}=\frac{5.29\times 10^{-11}\,\mathrm{m}}{6^{1/3}}
\simeq 2.91\times 10^{-11}\,\mathrm{m}=2.91\times 10^{4} \,\mathrm{fm}
\end{equation}
これは式 (21) の炭素原子核の半径 \(r_n\sim 2.5\,\) fm に比べると非常に大きい．よって, 式 (22) の鍵括弧中の第 2 項にある \((a q/\hbar)^{-2}\) は無視してよい．よって式(22) は次のように近似される：
v(q)\simeq -\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}\Bigl[ 1+ F_n(q)-1 \Bigr]
=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}}F_n(q)
\end{equation}
すなわち「核の形状因子 \(F_n(q)\) を考える場合には, 原子内電子の遮蔽効果は無視してよい」と言えよう．
