断熱不変量

水素原子スペクトルの「微細構造」に関連して「ボーア=ゾンマーフェルト模型」を調べていたら, 「断熱不変量」という物理量に遭遇した．朝永：「量子力学」§5 と M.ボルン：「現代物理学」の第5章から,「断熱不変量」についての文章を抜粋してまとめておく．

断熱不変量

〈朝永：「量子力学」§5より〉ある正弦振動を行なうような振動系があったとする．これは簡単な系で吊るした振り子であってもよいし, また引っ張られた弦のようなものでもよい．あるいは空洞内の輻射であってもよい．ただし空洞輻射といっても, 壁を通じて熱溜と熱エネルギーのやり取りをするものではなく, 完全に独立した輻射を考える．この力学系がある固有振動を行なっているとき,「その系の形をゆっくりと変化させて行く」．例えば, 振り子の糸をだんだん短くしたり弦の長さや張力を変化させたり, または空洞の壁の一つをピストン仕掛けにしておいてそれを中に押し込んだりする．そのとき,「この変形が十分ゆっくり行われると, 変化した後に, 系はやはり一つの固有振動を行なっている」ということが証明される．
このとき, 力学系の形の変化によって, もちろん固有振動の振動数 $\nu$ は変化して来るし, またその振幅も変化して来る．従って振動のエネルギー $E$ も変化して来る.それは言い換えると,「その変形の際に, それだけの仕事を行わなければならない」ということである．しかしそのとき注意すべきことは,「$E$ の変化の割合と $\nu$ の変化の割合とが相等しく, 従って $E/\nu$ はこの変化に於いて不変の値を持ち続ける」のである．この $J=E/\nu$ のことを「断熱不変量」という．もしも初めに系が固有振動の状態に無かったら, それは色々な固有振動を重ね合わせたもので表わすことが出来る．そうすると, 各々の固有振動毎に $E/\nu$ が不変なのである．

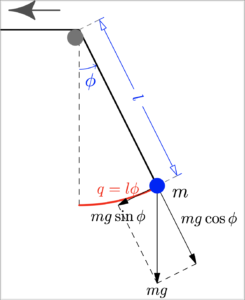
図3．長さを変え得る単振子．長さを十分ゆっくり短くするなら, 振動数 $\nu$ に対するエネルギー $E$ の比 $E/\nu$ は一定である．

〈M.ボルン：「現代物理学」第1章§2から抜粋〉以上の事実を簡単な振り子の例で示そう．長さが例えば滑車を用いて手繰りながら変えることが出来るような単振り子を考えよう (図 3 参照)．もし糸を「ゆっくり縮める」ならば, 我々は第１に重力に対し, 第２に振動子の遠心力に対して仕事をすることになる．糸の長さが $l$ から $l+\Delta l$ に「ゆっくり変った」としよう．ただし $\Delta l$ は負であるとしておこう．そうすれば, 振り子は短かくされたことになる．糸を引いている重さの成分は $mg\cos\phi$ であり, 遠心力は $ml\dot{\phi}^{2}$ である．$\dot{\phi}$ は角速度である．重力および遠心力に対して為された仕事 $W$ は,

\begin{equation}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\half{\frac{1}{2}}
W=\int_{l}^{l+\Delta l} \bigl\{mg\cos\phi + ml\dot{\phi}^{2}\bigr\}\,(-dl)
\tag{1}
\end{equation}

である．ところが糸を「非常にゆっくり短かくしている」と仮定しているのであるから, この変化の間に振り子は何回もあちらこちらに振動している．そこで振動の振幅の変化(すなわち振れ角 $\phi$ の変化) を糸の長さ $l$ に比べて無視し, 振幅 $l\cos\phi$ は一定である (従って $\cos\phi=$ 一定) として, 運動について積分すれば,

\begin{equation}
W=\left\{mg\,\overline{\cos\phi}+ml\,\overline{\dot{\phi}}\,\right\}\int_{l}^{l+\Delta l}\,(-dl)
=-\left\{mg\,\overline{\cos\phi}+ml\,\overline{\dot{\phi}}\,\right\}\Delta l
\tag{2}
\end{equation}

を得る．ただし「横線は変化を受けない運動についての平均を表す」．更に, もし微小振幅に限る ($\phi$ が微小) ならば, $\cos\phi$ を級数展開して $\cos\phi\approx 1-\phi^2/2$ と近似してよいから, 上式は次となる：

\begin{align}
W&=-\left\{mg\left(1-\half\overline{\phi^{2}}\right)+ml\,\overline{\dot{\phi}}\right\}\Delta l =-mg\,\Delta l + \left(mg\,\frac{\overline{\phi^{2}}}{2}-ml\,\overline{\dot{\phi}^{2}}\right)\Delta l \tag{3}\\
&= -mg\,\Delta l +\Delta E, \qquad\mathrm{where}\quad \Delta E=\left(mg\,\frac{\overline{\phi^{2}}}{2}-ml\,\overline{\dot{\phi}^{2}}\right)\Delta l \notag
\end{align}

第1項は平衡位置の上昇に対応するが, これは興味がない．第2項すなわちカッコ内の式と $\Delta l$ との積は「振り子運動」のエネルギー増加分 $\Delta E$ を表している．変化を受けない(元の)振り子運動のエネルギーは次である：

\begin{equation}
E = T+V= \frac{m}{2}(l\dot{\phi})^2 + mgl(1-\cos\phi)
\tag{4}
\end{equation}

この第1項は運動エネルギー $T$ を, 第2項は静止位置に対するポテンシャルエネルギー $V$ を表す．$1-\cos\phi$ を近似的に $\phi^{2}/2$ で置き換えれば,

\begin{equation}
E =\frac{m}{2}l^{2}\dot{\phi}^{2}+mgl\frac{\phi^{2}}{2}
=\half m (l\dot{\phi})^{2} + \half m\frac{g}{l}(l\phi)^{2}
=\half m\dot{q}^{2}+\half m\omega^{2}q^{2}
\tag{4′}
\end{equation}

しかしこれは丁度, 振幅が $q=l\phi$ なる線形振動子のエネルギー関数である．それゆえ運動は単調和振動 $\phi=\phi_0 \cos\omega t$ である．ゆえに,

\begin{equation}
\overline{\phi^{2}}=\phi_0^{2}\times \overline{\cos^{2}\omega t}=\frac{\phi_0^{2}}{2},\quad
\overline{\dot{\phi}^{2}}=\overline{(\phi_0(-\omega)\sin\omega t)^{2}}
=\phi_0^{2}\omega^{2}\times \overline{\sin^{2}\omega t}=\frac{\phi_0^{2}\omega^{2}}{2},
\tag{5}
\end{equation}

これから, $\displaystyle \omega=\sqrt{\frac{g}{l}}$ であるから, 容易に次式が得られる：

\begin{align}
E&=\frac{m}{2}l^{2}\overline{\dot{\phi}^{2}}+mgl\frac{\overline{\phi^{2}}}{2}
=\frac{m}{2}l^{2}\times\frac{\phi_0^{2}\omega^{2}}{2}+ mgl\half\times \frac{\phi_0^{2}}{2}
=\frac{1}{4}ml^{2}\phi_0^{2}\omega^{2}+\frac{1}{4}mgl\phi_0^{2}\notag\\
&=\frac{1}{4}ml^{2}\phi_0^{2}\omega^{2}+\frac{1}{4}m(l\omega^{2})l\phi_0^{2}
=\half ml^{2}\phi_0^{2}\omega^{2},\tag{6}\\
\mathrm{or}\quad E &=\frac{1}{4}ml^{2}\phi_0^{2}\frac{g}{l}+\frac{1}{4}mgl\phi_0^{2}
=\frac{1}{2}mgl\phi_0^{2}\notag
\end{align}

しかるに $W$ の表式 (3) の第2項 $\Delta E$に, 式 (5) とこの結果を用いると,

\begin{align}
\Delta E &=\left(mg\,\frac{\overline{\phi^{2}}}{2}-ml\,\overline{\dot{\phi}^{2}}\right)\Delta l
=\left(\half ml\,\omega^{2}\frac{\phi_0^{2}}{2}-ml\,\frac{\omega^{2}\phi_0^{2}}{2}\right)\Delta l
=\left(-\frac{1}{4}ml\,\omega^{2}\phi_0^{2}\right)\Delta l\notag\\
&=-\left(\half ml^{2}\phi_0^{2}\,\omega^{2}\right)\times \frac{1}{2l}\Delta l
= -\frac{E}{2l}\Delta l,
\tag{7}
\end{align}

従って,

\begin{equation}
\frac{\Delta E}{E}=-\half \frac{\Delta l}{l}
\tag{8}
\end{equation}

である．しかし他方, $\displaystyle \omega=2\pi\nu=\sqrt{\frac{g}{l}}$ より $\nu$ は $l^{-1/2}$ で変化する．$\displaystyle \nu=\frac{1}{2\pi}\sqrt{\frac{g}{l}}$ の両辺の微分をとると,

\begin{equation*}
d\nu=\frac{d\nu}{dl}dl =-\frac{\sqrt{g}}{2\pi}\frac{1}{2}l^{\,-3/2}\,dl
=-\frac{1}{2\pi}\sqrt{\frac{g}{l}}\times \frac{dl}{2l}=-\nu\frac{dl}{2l},
\quad \rightarrow\quad \frac{d\nu}{\nu}=-\frac{1}{2}\frac{dl}{l}
\end{equation*}

よって,

\begin{equation}
\frac{\Delta\nu}{\nu}=-\half \frac{\Delta l}{l},
\tag{9}
\end{equation}

この右辺は式 (8) の右辺に等しい．従って,

\begin{equation}
\frac{\Delta E}{E}=\frac{\Delta\nu}{\nu},\quad\mathrm{or}\quad \frac{dE}{E}=\frac{d\nu}{\nu}
\tag{10}
\end{equation}

である．これは $E$ を振動数 $\nu$ の関数と見た微分方程式で, その解は

\begin{equation}
\frac{E}{\nu}=Const=J
\tag{11}
\end{equation}

となる．このような振り子を「ゆっくり(断熱的に)縮めている間, $J$ という量(断熱不変量)は一定である」．よって「エーレンフェストの原理」から, これは $h$ の整数倍に等しいと置くことが出来る．すなわち,

\begin{equation}
E=n h\nu
\tag{12}
\end{equation}

従って, 調和振動子のエネルギー準位がプランクの基礎仮定と一致して得られたことになる．

他の力学系の断熱不変量も同様にして理論的に決定できる．しかしこの変換の方法は一般に非常に厄介であるから, 見出すのにより簡単な方法がないかどうかを考えて見よう．さて前の振動子の例(微小振動をする単振子)を特別な場合と考え,　不変量 $J=E/\nu$ を幾何学的に解釈することによって, それがどうしたら可能であるかを示そう．

エネルギーを幾分違った記号 $(q=l\phi,\ p=m\dot{q},\ f=mg/l)$ を用いてもうー度書き下すと,

\begin{equation}
E=\frac{1}{2m}p^{2}+\half fq^{2},\quad\rightarrow\quad
\frac{p^{2}}{2mE}+\frac{q^{2}}{2E/f}=1
\tag{13}
\end{equation}

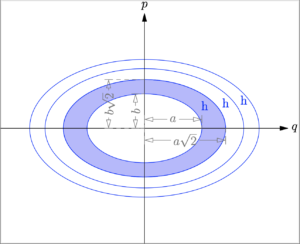
右式のように書き換えると, この式は $p$-$q$平面 (位相平面) で半軸 $a=\sqrt{2mE}$, $b=\sqrt{2E/f}$ を持つ楕円を表していることが分かる．楕円の面積は,

\begin{equation}
\oint p\,dq = \pi ab
\tag{14}
\end{equation}

であるから, この場合の面積は次となる：

\begin{equation}
\oint p\,dq = 2\pi E \sqrt{\frac{m}{f}}
\tag{15}
\end{equation}

(ただし記号 $\displaystyle\oint$ は, 全周期についての積分, 即ちここでは楕円の全周についての積分を意味している)．然るに $\displaystyle 2\pi\nu =\sqrt{f/m}$ であるから

\begin{equation}
\oint p\,dq = \frac{E}{\nu}=J
\tag{16}
\end{equation}

である．それ故に「断熱不変量とは単純に楕円の面積である」と言える．量子仮定で言えば,「位相平面 ($p$-$q$面) 内で描かれた閉曲線の面積は, 運動の一周期には $h$ の整数倍である」と言える (デバイ, 1913)．

図 4. 調和振動子の位相軌道．$p$-$q$平面(位相空間)では位相点が楕円を描き, その面積は$h$の整数倍だ．

このようにして定式化された闘係は直ちに一般化することができる．まず最初に, 自由度が $1$ なる場合の例として,「回転子」の円運動を考えてみる．そこでは座標は方位角 $q=\phi$ である．これに「正準共役」な「一般化運動量」として角運動量(即ち, 運動量の能率) $p=L$ が伴う．自由回転子では $L$ はー定, すなわち回転する角に無関係であるから,

\begin{equation}
J=\oint p\,dq =p\oint dq=\oint L\,d\phi =L\oint d\phi=2\pi L
\tag{17}
\end{equation}

である．もし運動を $p$-$q$ 面で表せば, この積分は閉曲線に沿ってでなく, $p=$一定なる直線に沿って取られるべきである．しかしこの面内で $q$-座標は $2\pi$ だけ違っているが, 同じ $p$ を持つ点はやはり回転子の同じ状態を表わすことに注意しなければならない．すなわち, 実を言えば $p$-$q$ 平面でなく, 周が $2\pi$ なる $p$-$q$-円筒を考えなければならない (第 5 図)．

図 5. 円筒面上に回転子の位相軌道を表している．

従って, 積分は円筒の周辺に沿って取られるべきであり, その値は $2\pi$ である．故に $J=2\pi L$ である．さて, もし我々の量子化規則

\begin{equation*}
J=\oint p\,dq = nh = 2\pi L
\end{equation*}

が正しいと仮定すれば, $L=n(h/2\pi)$ は前に全く別な方法で水素原子に対して発見した公式であるから, これが「帯スペクトル」を解釈するための回転子にうまく応用できることは当然であろう．

量子化規則 $\displaystyle \oint p\,dq=nh$ は自由度が $1$ なる体系にばかりでなく, 多くの自由度を持つ複雑な体系にも応用でき, しかも常に実験と一致する結果を得る．自由度が $1$ 以上の体系への拡張は, 多くの場合「一般化座標 $q_1,q_2,\dotsb$ が, それらに伴う一般化運動量 $p_i$ が $q_i$ のみに関係するような性質を持つ」ように導入されることで行われた (ゾンマーフェルト, W.Wilson, 1916)．この種の体系は「分離可能」であると言われる．一般にこれらは「多重周期」である．その場合には運動は単周期振動およびその調和振動の重ね合わせに分解される(いわゆるリサジューの図)．一例として, 一平面内での運動の例を考えよう．ここで直角座標 $x$ と $y$ は２つの振動数 $\nu_1$ と $\nu_2$ を持って振動している．もし $\nu_1$ が $\nu_2$ に等しいならば, 軌道は位相開係によって円, あるいは楕円になる．もし $\nu_2$ に対する $\nu_1$ の比が, ある有理数ならば, 軌道は再び閉じる．また, もし $\nu_1$ と $\nu_2$ が公約数を持たない, 即ちその比が有理数でないならば，曲線は閉じないで変数の動く範囲で矩形全体を漸次埋めて行く．一般に多重周期運動では, 軌道はこのような型になる．しかしながら, もし何回転か後に２つの軌道が閉じるならば, 実際には1周期だけがあって,

\begin{equation*}
\oint p\,dq = nh
\end{equation*}

なる形の「量子条件」が唯一つあることになろう．もし曲線が閉じないならば, 即ち２つ或はそれ以上の通約できない周期があるならば, その場合は周期のあるだけ量子条件がたくさんあることになろう:

\begin{align}
\oint p_1\,dq_1 = n_1 h,\quad \oint p_2\,dq_2 = n_2 h,\quad \dotsb
\tag{18}
\end{align}

これは一般の場合であって, また「非縮退」と考えられる場合であるが, これに反し, 一致したあるいは通約できる周期を持っている場合は「縮退している」と言われる．もし $u$ が周期の数で $v$ が自由度の数であるならば, そのとき $w=v-u$ を「縮退度」と言う．

このような古典力学と量子条件との奇妙な組合わせは, 整数 $n_1,n_2,\dotsb$ がもっと自然な方法で入ってくる首尾一貫した「量子力学」で置き換えられてしまった．しかしながら,「対応原理」から期待できるように, この理論は近似的ではあるが高い量子数に対しては (即ち $h$ が積分 $\displaystyle \oint p\,dq$ の値に比べて小さいならば) 成り立つのである．

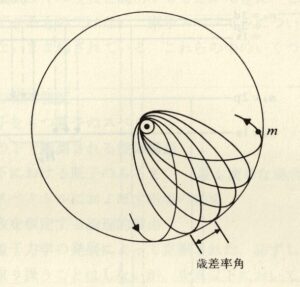
上の規則の一例として,「水素原子についてゾンマーフェルトが行った完全な量子条件」について議論しよう．ケプラーの法則によれば, 核の周りの電子の軌道は楕円である．それ故に単周期運動である．電子は3つの自由度を持っているから, これは2重に縮退している例である($3-1=2$)．縮退は「質量の相対論的変化」すなわち「電子の質量がその速度に関係すること」を考慮することによって一部が取り除かれる．この場合には軌道は, ゾンマーフェルトにより「歳差楕円」(バラ結び)となり, その長軸は核の周りを一定の角速度で楕円面内で回転する (第 7 図)．

図 7. 核の周りの電子のバラ型軌道．これは質量が相対論的に変わることを説明している．運動は2重周期的であり, 近日点は回転毎に角度 $\Delta\phi$ だけ変位する．

さて軌道は2重周期であるから歳差運動が小さいときには, 回転初期の不変な周期の他に「歳差運動の周期」が必要になる．このため２つの量子条件がこのときは必要である：

\begin{equation}
J_1 = nh,\quad J_2 = kh
\tag{19}
\end{equation}

ここで $n$ は近似的な楕円の半長軸 $a$ を決め $k$ はその半直弦を決める：$a=n^{2}a_0$, $q=k^{2}a_0$．さらに計算の結果, 全角運動量は

\begin{equation}
p=L=\hbar k,\quad\mathrm{where}\quad \hbar =\frac{h}{2\pi}
\tag{20}
\end{equation}

であり, しかもエネルギーはバルマー項の他にもう一つ項を含んでいる：

\begin{equation}
E= -\frac{R_0 h Z^{2}}{n^{2}} + \varepsilon(n,k)
\tag{21}
\end{equation}

式 (20) から $k=0$ のときは角運動量は消える．これは「振り子」の場合であり, 軌道楕円は縮退して「直線」になる．$k=n$ の場合は, ある固定した $n$ に対し最大可能な角運動量が得られ, これは「円軌道」になる．$k<n$ に対しては「楕円軌道」になる．スペクトルでは「振り子軌道」に対応したエネルギー項の徴候(サイン)は何ら見出されなかった．エネルギー項が現れないのであるから, 理論的には「それはスペクトル項から除かなければならない」．エネルギー項を除く理由はこうである：「振り子軌道は核を通過することになり, そのため電子は核と衝突することになる．これは勿論不可能である」．

次に付加項 $\varepsilon(n,k)$ についてだが, 水素スペクトル線について一層詳しいことを表している．この効果により, 全てのバルマー項は量子数 $k$ に対応する多くのエネルギー項に分かれる．それゆえ, スペクトル線自身が微細な線の系から出来上がっていることになり, それは上位状態 $n=n_1,k=1,2,\dotsb,n_1$ と下位状態 $n=n_2,k=1,2,\dotsb,n_2$ 間の遷移によって決定される．これをスペクトル線の「微細構造」と言う．その理論は水素型の原子 $(\mathrm{H},\mathrm{He}^{+},\mathrm{Li}^{2+})$ に対してはゾンマーフェルトによって与えられ, 一価にイオン化したヘリウム $(\mathrm{He}^{+})$ についてはファウラー(A.Fowler) 及びパッシェンによって実験され, 理論と完全に一致することが分かった．$(\mathrm{He}^{+})$ については実験が $(\mathrm{H})$ の実験よりも容易であることは次の理由に依る．すなわち $(\mathrm{He}^{+})$ のエネルギー項は, 核電荷数が２倍であるため４倍だけ離れている．しかるに微細構造の分離に対応する因子は, 理論が示すように$16$である ^[3][ブログ註] ボーア-ゾンマーフェルト模型に於ける水素類似原子のエネルギー準位は次式により与えられる： \begin{equation*} E_n=-\frac{RZ^{2}}{n^{2}} – … Continue reading．従って $(\mathrm{He}^{+})$ の微細構造はずっと容易に立証され, かつ測定される．

References[+]

References
↑1	[ブログ註] 単振り子の復元力は錘に働く重力の振動方向成分 $\displaystyle -mg\sin\phi\approx -mg\,\frac{g}{l}$ である (図 3 参照)．バネ振り子でこれに相当するのは $-kq=-m\omega^{2}q$ であるから $\displaystyle k=m\omega^{2}=\frac{mg}{l}$ 従って $\displaystyle \omega^{2}=\frac{g}{l}$ である．調和振動子のエネルギーは振幅を $q$ として次式で表される： \begin{equation} E=\half m\dot{q}^{2}+\half m\omega^{2}q^{2} \end{equation}
↑2	[ブログ註] 「Ehrenfest の断熱仮説」: 力学系に外部から何らか変化を与えるとき, この変化が無限にゆっくりと行われるなら, その経過の途中, 力学系の運動を通常の力学を用いて論ずることが許される．そしてこのとき, 変化の始まる前に系が量子的に許される状態(整数値のみを取り得る量によって表される状態)にあれば, この変化の途中およびその後に於いて系はいつも量子的に許される状態にある．従って, これらの量は変化を受けると, ある整数だけひとっ飛びに変わるか, 或いは変わらないままでいるかの何れかである．系に作用する変化がゆっくり行われるならば, 後の場合が起こるに違いない．即ちこの場合, これらの量は「断熱的に不変」であるという．従って「断熱的不変量」だけが量子化できると言ってもよい．(朝永,ボルンより)
↑3	[ブログ註] ボーア-ゾンマーフェルト模型に於ける水素類似原子のエネルギー準位は次式により与えられる： \begin{equation} E_n=-\frac{RZ^{2}}{n^{2}} – \frac{\alpha^{2}RZ^{4}}{n^{3}}\left(\frac{1}{k}-\frac{3}{4n}\right) \end{equation} すなわち, 付加項は $\displaystyle \varepsilon=- \frac{\alpha^{2}RZ^{4}}{n^{3}}\left(\frac{1}{k}-\frac{3}{4n}\right)$ である．ただし $R=me^{4}/4\pi\hbar^{3}c$ はリュードベリ定数, $\alpha=e^{2}/\hbar c$ は微細構造定数である．従って, 核電荷数 $Z$ が２倍になると付加項の微細構造因子は $Z^{4}\to 2^{4}=16$ 倍となる．

月	火	水	木	金	土	日
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31