\(\)
Fourteenth Lecture
行列要素の求め方(METHODS OF OBTAINING MATRIX ELEMENTS)
始状態 \(u_1\) と終状態 \(u_2\) 間での演算子 \(M\) の行列要素は, 次で表現されるであろう：
\(
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\def\half{\frac{1}{2}}
\def\slashed#1{#1\llap{/}\,}
\def\slashW{W\!\!\llap{/}\,}
\def\BraKet#1#2#3{\left\langle #1 | #2 | #3 \right\rangle}
\def\BK#1#2{\left\langle #1 | #2 \right\rangle}
\)
(\tilde{u}_2 M u_1)
\end{equation*}
ガンマ行列の表示がユニタリーな等価変換 \(S\) で関係しているならば, 行列要素は表示には依存しない．すなわち [1][訳註] 変換 \(S\) は特性 \(\tilde{S}=S^{-1}\) を持つと仮定するので, この \(S\) は数学的に厳密な「ユニタリー」ではない．\(S^{\dagger}S=1\) ではなく … Continue reading,
\begin{align*}
u’_{1}=Su_{1},\quad u’_{2}=Su_{2},\quad M’ = S M S^{-1}= S M S^{\dagger},\quad
\tilde{u’}_{2}=\tilde{u}_2\tilde{S}
\end{align*}
従って,
\tilde{u’}_{2} M’ u’_{1}=(\tilde{u}_{2}\tilde{S})(S M S^{-1})(Su_{1})
=\tilde{u}_{2}(S^{-1}S) M (S^{-1}S) u_{1}=\tilde{u}_{2}M u_{1}
\end{equation*}
ただし, 変換 \(S\) は特性 \(\tilde{S}=S^{-1}\) を持つと仮定している．
行列要素を計算する簡単な方法は, 単純に行列形式で書き出し, 演算を実行することである．このようにして, 第13講の表 13-1 のデータが得られた．しかし他の方法を用いてもよく, 次の例で示すように, より単純で, 時には補足的な情報を導くこともある．規格化の取り決めにより,
\tilde{u}u = 2mc^{2}
\end{equation*}
従って, 方程式 \(\slashed{p}u=mc\,u\) を用いると,
(\tilde{u}\slashed{p}u)=\tilde{u}(\slashed{p}u)=\tilde{u}(mc\,u)
=mc(\tilde{u}u)=mc\times 2mc^{2}=2m^{2}c^{3}
\end{equation*}
同様にして,
(\tilde{u}\gamma^{\mu}\slashed{p}u)=\tilde{u}\gamma^{\mu}(\slashed{p}u)
=\tilde{u}\gamma^{\mu}(mc\,u)=mc(\tilde{u}\gamma^{\mu}u)
\tag{A}
\end{equation*}
しかし, 関係式 \(\tilde{u}\slashed{p}=\slashed{p}\tilde{u}=mc\tilde{u}\) が言えるので次式も成立することに注意しよう：
(\tilde{u}\slashed{p}\gamma^{\mu}u)=(\tilde{u}\slashed{p})\gamma^{\mu}u
=(mc\tilde{u})\gamma^{\mu}u=mc(\tilde{u}\gamma^{\mu}u)
\tag{B}
\end{equation*}
上の式 (A) と (B) を足し合わせると次式が得られる：
(\tilde{u}[\gamma^{\mu}\slashed{p}+\slashed{p}\gamma^{\mu}]u)
=2mc(\tilde{u}\gamma^{\mu}u)
\tag{C}
\end{equation*}
更に, 練習問題で証明した次の関係式
\slashed{a}\slashed{b}+\slashed{b}\slashed{a}=2a\cdot b,\qquad a\cdot b = a^{\mu}b_{\mu}
\end{equation*}
に於いて,
\slashed{a}=\slashed{p}=p_{\nu}\gamma^{\nu},\quad
\slashed{b}=b_{\nu}\gamma^{\nu}=\eta^{\mu}_{\ \nu}\gamma^{\nu}=\delta^{\mu}_{\ \nu}\gamma^{\nu}=\gamma^{\mu}
,\quad \eta^{\mu\rho}\eta_{\rho\nu}=\eta^{\mu}_{\ \nu}=\delta^{\mu}_{\ \nu}=I
\end{equation*}
とするならば, 関係式 \(\gamma^{\mu}\gamma^{\nu}+\gamma^{\nu}\gamma^{\mu}=2\eta^{\mu\nu}\) を用いて次式が成り立つことが分かる：
\slashed{p}\gamma^{\mu}+\gamma^{\mu}\slashed{p}
=p_{\nu}\gamma^{\nu}\gamma^{\mu}+\gamma^{\mu}\gamma^{\nu}p_{\nu}
=\bigl(\gamma^{\nu}\gamma^{\mu}+\gamma^{\mu}\gamma^{\nu}\bigr)p_{\nu}
=2\eta^{\mu\nu}p_{\nu} = 2p^{\mu} ,\quad \gamma^{\mu}
=\delta^{\mu}_{\ \nu}\gamma^{\nu}=\slashed{I}
\tag{D}
\end{equation*}
しかしながら \(p^{\mu}\) は単なる数値である．従って, 式 (C) と式 (D) から次が言える：
(\tilde{u}[\gamma^{\mu}\slashed{p}+\slashed{p}\gamma^{\mu}]u)
=\tilde{u}2p^{\mu}u = 2p^{\mu}(\tilde{u}u)=2mc(\tilde{u}\gamma^{\mu}u)
\end{equation*}
そして規格化により \(\tilde{u}u=2mc^{2}\) であったので,
2p^{\mu}\times 2mc^{2}=2mc(\tilde{u}\gamma^{\mu}u)\quad\rightarrow\quad
(\tilde{u}\gamma^{\mu}u)=2c p^{\mu}
\end{equation*}
この結果または前節の式 (3) を用いると, さらに次の一般的関係が得られる：
\frac{(\tilde{u}\gamma^{\mu}u)}{(\tilde{u}u)}=\frac{2cp^{\mu}}{2mc^{2}}=\frac{p^{\mu}}{mc},
\quad\rightarrow\quad
\frac{(\tilde{u}\gamma^{0}u)}{(\tilde{u}u)}=\frac{p^{0}}{mc}=\frac{2E}{2mc^{2}}=\frac{E}{mc^{2}}
\end{equation*}
相対論的に不変な規格化の可能性は4元ベクトルの第 0 成分に等しくすることであったから
\frac{(\tilde{u}\gamma^{\mu}u)}{(\tilde{u}u)}=\frac{(\tilde{u}\gamma^{0}u)}{(\tilde{u}u)}=
\frac{E}{mc^{2}}
\end{equation*}
としてみる．すると次式の規格化は \((\tilde{u}u)=1\) としたことに等しい：
(\tilde{u}\gamma^{\mu}u)=\frac{E}{mc^{2}}
\end{equation*}
【 問題 】次式が成立することを, 今まで説明した方法と同じやり方で示してみよ：
(\tilde{u}\gamma^{5}u)=0
\end{equation*}
〈解答例〉本文解説の式 (A) 及び式 (B) と同様にして,
\begin{align*}
(\tilde{u}\gamma^{5}\slashed{p}u)&=\tilde{u}\gamma^{5}(\slashed{p}u)
=\tilde{u}\gamma^{5}(mcu)=mc(\tilde{u}\gamma^{5}u),\tag{1}\\
(\tilde{u}\slashed{p}\gamma^{5}u)&=(mc\tilde{u})\gamma^{5}u=mc(\tilde{u}\gamma^{5}u),\tag{2}
\end{align*}
式 (1) と式 (2) を足し合わせると,
(\tilde{u}[\gamma^{5}\slashed{p}+\slashed{p}\gamma^{5}]u)=2mc(\tilde{u}\gamma^{5}u)=0
\tag{3}
\end{equation*}
ところが, 交換関係 \(\gamma^{5}\gamma^{\mu}+\gamma^{\mu}\gamma^{5}=0\) より次が言えるので, 上式 (3) はゼロであることが分かる：
\gamma^{5}\slashed{p}+\slashed{p}\gamma^{5}
=\gamma^{5}\gamma^{\mu}p_{\mu}+\gamma^{\mu}p_{\mu}\gamma^{5}
=(\gamma^{5}\gamma^{\mu}+\gamma^{\mu}\gamma^{5})p_{\mu}=0
\tag{4}
\end{equation*}
よって,
(\tilde{u}\gamma^{5}u)=0
\end{equation*}
負エネルギー状態の解釈(INTERPRETATION OF NEGATIVE ENERGY STATES)
Dirac方程式の解が存在するための必要条件は, 前述により式 (13-10) であることが分かっている：
E^{2}=c^{2}\mb{p}^{2}+m^{2}c^{4}\quad\rightarrow\quad
E=\pm\sqrt{c^{2}\mb{p}^{2}+m^{2}c^{4}}
\end{equation*}
「正のエネルギー」の意味は明らかであるが,「負のエネルギー」の意味はそうではない．シュレーディンガーは一時期,「負のエネルギー」には意味がないとして恣意的に排除するべきだと提案した．しかし, 負のエネルギー状態を排除することには２つの根本的な難点 (objection) があることが分かった．一つは物理的な難点, すなわち理論物理的な難点である．ディラック方程式の場合,「正のエネルギー状態から出発しても, 負のエネルギー状態へ誘導遷移する確率が存在する」という結果をもたらすからである．従って, それらを排除するならば, これは矛盾しているであろう．２番目は数学的な難点である．すなわち, 負のエネルギー状態を排除すると, 波動関数が完全集合にならない(incomplete set of wave function) からである．任意の関数を完全でない集合の関数で展開することは不可能なのである．この状況は, シュレディンガーを克服できない困難(insurmountable difficulties) に導いてしまった．
【 問題 】\(t<0\) のとき, 粒子は正のエネルギー状態にあり \(z\) 方向にスピン \((s=+1)\) を持ち \(x\) 方向を運動していると仮定する．そして \(t=0\) で一定なポテンシャル \(\mb{A}=A_{z}(A_x=A_y=0)\) が印加され, それは \(t=T\) で消えるとする．この時刻 \(t=T\) に於いて, 粒子が負のエネルギー状態にある確率を見出せ．
(答え)：\(t=T\) で負のエネルギー状態に在る確率 \(\mathrm{Prb}\) は, 次である：
\end{equation*}
(注意) \(E=-mc^{2}\) で \(1/\sqrt{F}=\infty\) のとき, スピノル \(u\) は明らかに`爆発する(blow up)’． しかし \(E=-mc^{2}\) のとき, 実際にはスピノル \(u\) の成分もゼロとなってしまう．従って, 極限過程は必然的に含まれている．単純に \(1/\sqrt{F}\) を省略し, そして \(u\) 成分中の \(F\) をゼロそして \(p_{\pm}\) を \(1\) に置き換えるだけで, この極限過程は避けることが出来て, 正しい結果が得られる．
〈解答例〉題意よりこの摂動は, 下の左図のような鋸歯状に時間変化する摂動ポテンシャルと見做せる．従って, 問題は「時間に依存する摂動論」で扱えばよいであろう．
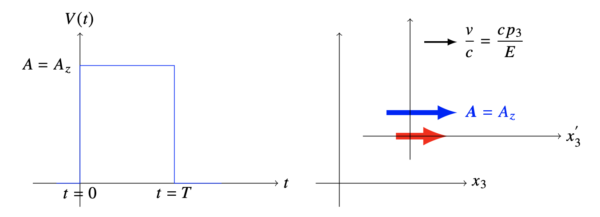
図 14.1 (左図)：摂動ポテンシャルの時間変化．(右図)：電子が正のヘリシティーを持ち \(x_3\) 軸方向に運動量 \(\mb{p}\) で運動している．この電子が静止して見えるような \(x’_{3}\) 座標系を選択する．太い赤色の矢印はスピンの向きを表す．
時間を含む摂動論の遷移振幅 \(c_n(t)=\BraKet{n}{U_I(t,t_0)}{i}\) の「１次の振幅 \(c_n^{(1)}\)」は次で与えられた：
c_{n}^{(1)}=-\frac{i}{\hbar}\int_{t_0}^{t}\BraKet{n}{V_I(t’)}{i}\,dt’
=-\frac{i}{\hbar}\int_{t_0}^{t}e^{i\omega_{ni}t’}V_{ni}(t’)\,dt,\quad
\omega_{ni}=\frac{E_n-E_i}{\hbar}
\tag{1}
\end{equation*}
「\(t=0\) で摂動 \(V(t)\) が印加され, その摂動は一定値 \(V_0\) を保つ」という特別な場合のハミルトニアンを考える：
H=H_0 + V(t),\quad
V(t)=\begin{cases}
0, & t<0 \\ V_0, & t>0
\end{cases}
\tag{2}
\end{equation*}
時刻 \(t=0\) で初期状態は固有状態 \(\ket{i}\) に在るならば, 行列要素は次となる：
\BraKet{n}{V_I(t’)}{i}=\bra{n}e^{iH_0 t/\hbar}{V(t)}e^{-iH_0t/\hbar}\ket{i}
=V_{ni}e^{i(E_n-E_i)t/\hbar}=V_{ni}e^{i\omega_{ni}t}
\end{equation*}
従って, 時間 \(t_0=0\) から \(t=T\) までを考えると, 上式 (1) は次となる：
c_{n}^{(1)}=-\frac{i}{\hbar}V_{ni}\int_{0}^{T}e^{i\omega_{ni}t’}\,dt’
=\frac{V_{ni}}{E_n-E_i}\bigl(1-e^{i\omega_{ni}T}\bigr),\quad
V_{ni}=\BraKet{n}{V_I}{i}=V_0\BK{n}{i}
\tag{3}
\end{equation*}
よって, 一次の遷移確率は次で与えられる：
\mathrm{Prb}=\left|c_{n}^{(1)}\right|^{2}
=\frac{\left|V_{ni}\right|^{2}}{\left|E_n-E_i\right|^{2}}
\bigl(2-2\cos\omega_{ni}T\bigr)
=\frac{4\left|V_{ni}\right|^{2}}{\left|E_n-E_i\right|^{2}}
\sin^{2}\left[\frac{(E_n-E_i)T}{2\hbar}\right]
\tag{4}
\end{equation*}
電磁相互作用を含む Dirac 方程式のハミルトニアンは, 式 (10.24) から次である：
H=c\mb{\alpha}\left(\mb{p}-\frac{e}{c}\mb{A}\right) + e\phi + \beta mc^{2}
=\bigl[c\mb{\alpha}\cdot\mb{p}+ e\phi + \beta mc^{2}\bigr] -e\mb{\alpha}\cdot\mb{A}
\tag{5}
\end{equation*}
これは次のように書き直すことが出来る：
H = H_0 + V,\quad\mathrm{where}\quad H_0=c\mb{\alpha}\cdot\mb{p}+ e\phi + \beta mc^{2},\quad
V=-e\mb{\alpha}\cdot\mb{A}
\tag{6}
\end{equation*}
このとき, \(H_0\) は外場の印加されていないときの自由粒子のハミルトニアンであり, そして \(V\) は自由粒子に作用する摂動ポテンシャルと見做せる．これを今の問題に適用するならば,
H_0=c\alpha_1 p_x +\beta mc^{2},\quad V=-\alpha_3 eA_z=-\gamma^{0}\gamma^{3} eA_z
\tag{7}
\end{equation*}
始状態のスピノールは, ローレンツ逆変換 \(S^{-1}\) によって粒子が静止して見える座標系においては \(p_{+}=0\), \(E=mc^{2}\), \(F=2mc^{2}\) として次となる：
u_{i}=\frac{1}{\sqrt{2mc^{2}}}\begin{pmatrix} mc^{2}+mc^{2} \\ 0 \\ 0 \\ 0 \end{pmatrix}
=\sqrt{2mc^{2}}\begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}
\tag{8}
\end{equation*}
他方, 終状態である負エネルギーのスピノール \(u_{f}\) は, 同じ座標系から見て次とする：
u_{f}=v^{(2)}=\frac{1}{\sqrt{F_2}}\begin{pmatrix} cp’_{3} \\ 0 \\ F_2 \\ 0 \end{pmatrix},
\quad F_2=|-mc^{2}|+mc^{2}=2mc^{2}
\tag{9}
\end{equation*}
以上から摂動 \(V\) の行列要素は,
\begin{align*}
V_{fi}&=u^{\dagger}_{f}Vu_{i} =-(u^{\dagger}_{f}\gamma^{0}\gamma^{3}eA_{z}u_{i})
= -eA_{z}(\tilde{u}_{f}\gamma^{3}u_{i})
=-eA_{z}2mc^{2}\begin{pmatrix} cp’_{3} & 0 & -1 & 0 \end{pmatrix}
\begin{pmatrix} 0 \\ 0 \\ -1 \\ 0 \end{pmatrix}\\
&=-2mc^{2}eA_{z}\quad\rightarrow\quad -eA_{z}
\tag{10}
\end{align*}
ただし \(2mc^{2}\) は, 式 (13-14) 規格化条件から由来しているので除いておく．
また, エネルギー変化 \(\Delta E = (E_{f}-E_{i})\) は運動量変化 \(\Delta p=(p_f-p_i)\) を用いて次のように表せる：
E_{f}-E{i} = \Delta E =\sqrt{c^{2}(\Delta p)^{2}+m^{2}c^{4}}
\tag{11}
\end{equation*}
ここで, 第 11 講義の問題から, 場が静的な場合に次の量は「運動の定数」であった：
\mb{\Sigma}\cdot\left(\mb{p}-\frac{e}{c}\mb{A}\right)
\tag{12}
\end{equation*}
これを今の場合の終状態 \((\mb{p}’_{3},\mb{A}=A_z)\) と初状態 \((\mb{p}=\mb{A}=0)\) とに当てはめるならば,
\mb{\Sigma}\cdot\left(p’_{3}-\frac{e}{c}A_z\right)=\sigma_3\left(p’_{3}-\frac{e}{c}A_z\right)=0,
\quad\rightarrow\quad cp’_{3}=eA_{z}
\tag{13}
\end{equation*}
従って, 運動量変化 \(c\Delta p\) は \(eA_z\) を \(A\) と表記し直してしまえば \(A\) と見積もれる：
\Delta (cp) = cp’_{3}-0 = A
\tag{14}
\end{equation*}
すると, 式 (11) のエネルギー変化は次のように書ける：
E_{f}-E_{i}=\sqrt{(\Delta cp)^{2}+m^{2}c^{4}}=\sqrt{A^{2}+m^{2}c^{4}}
\tag{15}
\end{equation*}
以上の結果式 (10), 式 (15) を式 (4) に用いると,「遷移確率」として次式を得る：
\mathrm{Prb}=\left|c_{n}^{(1)}\right|^{2}
=\frac{4|-A|^{2}}{A^{2}+m^{2}c^{4}}
\sin^{2}\left[\frac{\sqrt{A^{2}+m^{2}c^{4}}T}{2\hbar}\right]
\tag{16}
\end{equation*}
更に \(\theta\) が微小であるときには, 次のような近似が可能であろう：
\sin\frac{\theta}{2}\approx \frac{\theta}{2}\approx \frac{\sin\theta}{2},
\quad\rightarrow\quad \sin^{2}\frac{\theta}{2}\approx \frac{\sin^{2}\theta}{4}
\tag{17}
\end{equation*}
これを用いるならば, 結果式 (16) は問題に示された回答となり得る：
\begin{align*}
\mathrm{Prb}
&=\frac{A^{2}}{A^{2}+m^{2}c^{4}}\times 4\times\frac{
\sin^{2}\left[\sqrt{A^{2}+m^{2}c^{4}}\bigl(T/\hbar\bigr)\right]}{4}\\
&=\frac{A^{2}}{A^{2}+m^{2}c^{4}}\sin^{2}
\left[\sqrt{A^{2}+m^{2}c^{4}}\bigl(T/\hbar\bigr)\right]
\tag{18}
\end{align*}
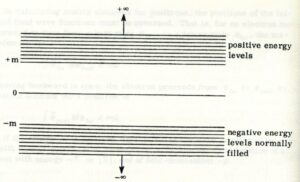
正エネルギー準位は \(E=mc^{2}\) から \(+\infty\) まで続く連続体を形成している．そして負エネルギーも同様に認めるならば, もう一つの連続体を \(E=-mc^{2}\) から \(-\infty\) まで形成している．\(+mc^{2}\) と \(-mc^{2}\) の間に, 占有できるエネルギー準位は存在しない (図 14-2 を参照)．
図 14-2
ディラックは「通常では負のエネルギー準位はすべて占有されている」という考えを提唱した．「負エネルギー状態の電子の海」という不明瞭に思えるものがもし存在するとしても, そのような説明は大抵心理学的な側面を含んでおり, あまり納得のいくものではない．しかしながら, もしそのような状況が存在すると仮定されるならば, 重要な結論が幾つか得られる：
- 正エネルギー状態の電子は通常では負エネルギー状態へ遷移することは観測されない．なぜなら, それらの状態はすでに充満しているので利用できないからである．
- 負エネルギー準位の電子の海が観測出来なくても, 準位中の一つの電子が正エネルギー準位へ遷移することで海の中に「ホール」が生成するというのは明瞭である．ホールの出現は「陽電子」と見做され, 正電荷を持つ電子の様に振る舞う．
- 負の海が満たされているためには「パウリの排他原理」が関係している．すなわち, ある状態に 1 個だけでなく任意個の電子が占有するとしたならば, 全ての負エネルギー状態を万杯にすることは不可能だからである．この様にして, ディラック理論は排他原理の証拠と見做されることがある．
著者は負エネルギー状態の別の解釈を提案している．基本的な考えは, `負エネルギー’状態は「時間を逆行する電子の状態」だというものだ．
古典力学的な運動方程式
m\frac{d^{2}z_{\mu}}{ds^{2}} = e\frac{dZ_{\nu}}{ds}F_{\mu\nu}
\end{equation*}
に於いては,「時間を逆行する」ことは「電荷を逆にする」ことと同じになり, 従って「時間を逆行する電子」は「時間を順行する陽電子」のように見える．
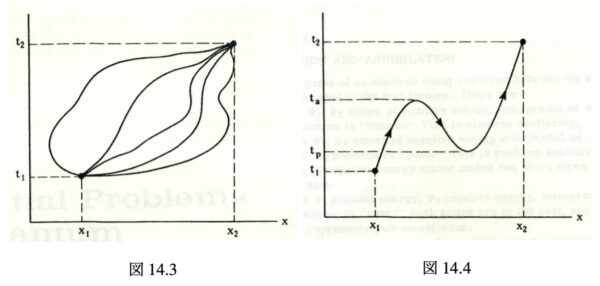
初歩的な量子力学において, 電子が \((x_1,t_1)\) から \((x_2,t_2)\) へ行くための全振幅は \((x_1,t_1)\) と \((x_2,t_2)\) の間の全ての可能な経路にわたって振幅を合計することによって計算される．その際には, 経路は常に時間的に順行すると仮定する．これらの経路は図 14.2 に示すように 1 次元で現れるかも知れない．しかし, 新しい観点では, 可能な経路は図 14.3 に示すようになるかも知れない．「観察者は普通に時を刻んでいて, 現在と過去のみが分かる」と自分自身を想像すると, 一連の事象は以下のように見えるであろう：
\(t_1 \to t_p\) : 最初の電子のみが存在する．
\(t_p\to\quad\) : 最初の電子はまだ存在するが, 何処か別の場所で電子と陽電子の対が形成される．
\(t_p \to t_a\) : 最初の電子と新たに出現した電子と陽電子が存在する．
\(t_a \to\quad\,\) : 陽電子は最初の電子と出会い, 両方とも消滅し, 以前に生成された電子だけが残る．
\(t_a \to t_2\,\) : 電子のみが存在する．
この考えを量子力学的に扱うためには次の2つの規則に従わなければならない：
- 陽電子の行列要素を計算するには,始状態と終状態の波動関数は逆でなければならない．すなわち, 電子が時間を過去の状態 \(\psi_{\mathrm{past}}\) から未来の状態 \(\psi_{\mathrm{fut}}\) へと前向きに移動する場合, 行列要素は次となる：
\begin{equation*}
\int \tilde{\psi}_{\mathrm{fut}}\, M\, \psi_{\mathrm{past}}\,d Vol
\end{equation*}
しかし時間を逆行する時, 電子は \(\psi_{\mathrm{fut}}\) から \(\psi_{\mathrm{past}}\) へ進むので, 陽電子の行列要素は次となる：
\begin{equation*}
\int \tilde{\psi}_{\mathrm{past}}\, M\, \psi_{\mathrm{fut}}\,d Vol
\end{equation*} - エネルギー \(E\) が正であると, 因子 \(e^{-ip\cdot x/\hbar}\) はエネルギー \(cp_0=E\) を持つ「電子」の波動関数である．もし \(E\) が負であると, 因子 \(e^{-ip\cdot x/\hbar}\) はエネルギー \((-E)\) または \(|E|\) そして４元運動量 \((-\mb{p})\) を持つ「陽電子」の波動関数である．
References
| ↑1 | [訳註] 変換 \(S\) は特性 \(\tilde{S}=S^{-1}\) を持つと仮定するので, この \(S\) は数学的に厳密な「ユニタリー」ではない．\(S^{\dagger}S=1\) ではなく \(S^{\dagger}\gamma^{0}S=1\) となるからである． |
|---|
