記事「式 (8-79) の再考察」の修正

2021.09.04

Feynman-Hibbs-cover
\(\)
はてなブログ：「ファインマンさんの肩に乗って晴耕雨読の日々」の２つの記事(2017年８月16日, 31日) は適切でないように思えたので削除し, その代わりとして, 改めてその部分の本文の文章
§ 8-4 THE ONE-DIMENSIONAL CRYSTAL —- Solving the Classical Equations of Motion.
を, 多少の補足を加えて示しておく．

古典的運動方程式の解 (Solving the Classical Equations of Motion)

変位 \(q\) は振動数 \(\omega\) で周期的変動をすると仮定する．すると \(\ddot{q}_j=-\omega^{2}q_j\) と出来るから, 式 (8-68) と一緒にして次式を解かなければならない：

\begin{equation}
-\omega^{2}q_j= \nu^{2}(q_{j+1}-2q_j+q_{j-1})
\tag{8-70}
\end{equation}

この連立方程式を行列式の形に表わすことも出来, その行列式方程式は数学の定理によって評価することが出来る．しかし, このことは方程式が直接解けるということを意味するのであるから, 直接解いてしまう方が簡単である．
記号 \(i\) は \(\sqrt{-1}\) を意味するものとし, 添字としては用いないことにする．解は次のようになる：
\[q_j=A\,e^{i(Kj-\omega t)}=Ae^{iK j}e^{-i\omega t}\equiv a_j^{*}\,e^{i\omega t}, \qquad \mathrm{where}\quad a_j = A e^{-iKj}\tag{8-71}\]
ただし \(K\) は離散的な値をとる定数である．(また, この \(a_j\) には時間 \(t\) が含まれないことに注意する)．これが解であることは,　式 (8-70) に代入することによって確かめられる．そして振動数は次式で与えられる：
\begin{align}
\def\reverse#1{\frac{1}{#1}}
\def\half{\frac{1}{2}}
-\omega^{2}A e^{i(Kj-\omega t)}&=\nu^{2}\Bigl(Ae^{i(Kj+K-\omega t)}-2Ae^{i(Kj-\omega t)}+Ae^{i(Kj-K-\omega t)}\Bigr),\notag\\
\mathrm{therefore}\quad -\omega^{2}&=\nu^{2}(e^{iK}-2+e^{-iK})=\nu^{2}(2\cos K-2)=-2\nu^{2}\times 2\sin^{2}\frac{K}{2}\notag\\
&=-4\nu^{2}\sin^{2}\left(\reverse{2}K\right)
\tag{8-72}
\end{align}

ここで \(K\) によって \(\omega\) の値が与えられているが, \(K\) の全ての値が許されている訳ではない．周期的境界条件の式 (8-69) 中の \(q_{N+j}=q_j\) から， \(K=2\pi\alpha/N\) であるべきである：
\begin{align*}
&Ae^{iK(N+j)-i\omega t}=Ae^{iKj-i\omega t}\quad\rightarrow\quad e^{iK N}=1,\\
\mathrm{therefore} \quad & K N =2\pi \alpha \quad\rightarrow\quad K=\frac{2\pi}{N}\alpha,\quad \mathrm{where}
\quad \alpha=0,1,2,\dotsb,N-1
\end{align*}
ただし \(\alpha=0\) の場合は並進運動であり,　必要なら無視することが出来る．さらに,　\(\alpha=N+\alpha’\) の場合の振動数は \(\alpha’\) の場合と同じである．よって特定の \(\alpha\) の値に対して振動数 \(\omega_\alpha\) は次となる：
\begin{equation}
\omega^{2}=4\nu^{2}\sin^{2}\left(\reverse{2}\times\frac{2\pi}{N}\alpha\right) \quad\rightarrow\quad
\omega_\alpha=2\nu\left|\,\sin\frac{\pi}{N}\alpha\,\right|
\tag{8-73}
\end{equation}

この振動数 \(\omega_\alpha\) に対する \(j\) 番目の座標の振幅 \(a_{j,\alpha}\) または \(a_{j,-\alpha}=a^{*}_{j,\alpha}\) は次である：
\begin{equation}
a_{j,\alpha}=Ae^{-iK_{\alpha}j}=A\exp\left(-i\frac{2\pi}{N}\alpha j\right),\qquad
a_{j,-\alpha}=a_{j,\alpha}^{*}=A\exp\left(i\frac{2\pi}{N}\alpha j\right)
\tag{8-74}
\end{equation}

この最後の式で決定された定数 \(a_{j\alpha}\) は複素数である．\(\alpha\) と \(-\alpha\) (または \(\alpha\) と　\(N-\alpha\))　に対する解の結合を取ることにより, この定数を実数にすることも出来るであろう．しかし,　そのまま複素数の形にしておく方が便利である．また，\(\alpha\) の値として正と負の両方を考えると便利な場合がある．従って,　例えば \(N\) が奇数のときの \(\alpha\) の値域としては, \(0\) から \(N-1\) ではなくて, \(-(N-1)/2\) から \(+(N-1)/2\) を考えるとよい．
弦中の原子の相対的な変位は \(\alpha\) の大きさに依存する． \(\alpha\) の2つの値( \(\alpha\) の小さい場合と \(\alpha=N/2\) の場合)に対応する振動の様子を 図 8-3 に示した．

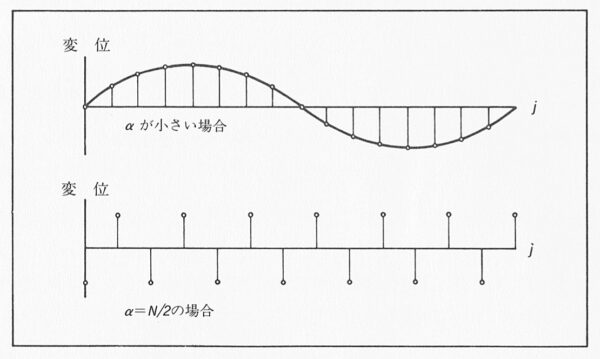
fig. 8-4

図 8-3. ひもの上に並んでいる原子の変位を縦軸にし, 横軸には等間隔に並んでいる平衡位置 j を示す．
上図の場合, 波長は原子間隔と比較して長い (\( \alpha\) が小さい)．
下図の場合, \(\alpha=N/2\) であり, 変位はもはや滑らかな正弦波の様相を示さない．

それぞれの定数 \(a_{j\alpha}\) の相対的な大きさは式 (8-74) によって決まるが, 定数 \(A\) によって決まる全体の大きさは任意である．これを式 (8-48) と類似の規格化方程式によって決定する．従って \(A\) は次式となるように選ぶ：

\begin{equation}
\sum_{j=1}^{N} a_{j\alpha}^{\,*}\,a_{j\beta} = \delta_{\alpha\,\beta}
\tag{8-75}
\end{equation}

これは \(\alpha=\beta\) の場合から, 次であることを意味する：
\begin{align}
\sum_{j=1}^{N} a_{j\alpha}^{\,*}a_{j\alpha}&=\sum_{j=1}^{N} Ae^{i2\pi\alpha j/N}Ae^{-i2\pi\alpha j/N}
=\sum_{j=1}^{N}A^{2}=NA^{2}=1\notag\\
&\mathrm{therefore}\quad A=\reverse{\sqrt{N}}
\tag{8-76}
\end{align}

さて今や我々は, 様々なモードを基準座標で表現する局面にある．式 (8-74) と式 (8-76) の結果から
\begin{equation*}
a_{j\alpha}=Ae^{-iK_\alpha j}=\frac{1}{\sqrt{N}}\exp\left(-i\frac{2\pi}{N}\alpha j\right)
\end{equation*}

従って, 基準座標は次のように表わすことが出来る：
\begin{equation}
Q_\alpha=\sum_{j=1}^{N} a_{j\alpha}q_j(t)=\sum_{j=1}^{N}\reverse{\sqrt{N}}\,\exp\left(-i\frac{2\pi}{N}\alpha j
\right)\,q_j(t)=\reverse{\sqrt{N}}\sum_{j=1}^{N}q_j(t)\,e^{-i2\pi\alpha j/N}
\tag{8-77}
\end{equation}

ただし式 (8-42) との類似性から, 変位は \(q_j(t)=\sum_{\alpha} c_\alpha a_{j\alpha}^{*}\,e^{-i\omega_\alpha t}\) である．．これらの基準座標も複素数である．しかし「それから得られるラグランジアンは実数であること」を, それを次のように書くことで保証することが出来る：
\begin{align}
L&=\reverse{2}\sum_{\alpha=0}^{N-1} \left(\dot{Q}_{\alpha}^{\,*}\dot{Q}_{\alpha}
-\omega_{\alpha}^{\,2}Q_{\alpha}^{\,*}Q_{\alpha}\right),
\tag{8-78}\\
\quad\text{or,}\quad
L&=\half\sum_{\alpha=-\half(N-1)}^{\half(N-1)}\left(\dot{Q}_{\alpha}^{\,*}\dot{Q}_{\alpha}
-\omega_{\alpha}^{\,2}Q_{\alpha}^{\,*}Q_{\alpha}\right)=\sum_{\alpha=0}^{\half(N-1)}\left(\dot{Q}_{\alpha}^{\,*}
\dot{Q}_{\alpha}-\omega_{\alpha}^{\,2}Q_{\alpha}^{\,*}Q_{\alpha}
\right)\tag{8-78′}
\end{align}

複素数の座標を用いることに関して一言述べておく必要がある． \(q_j\) は物理的座標であるから実数である．よって式 (8-77) は「 \(Q_\alpha^{\,*}=Q_{-\alpha}\) 」を含意している．すなわち, それぞれの複素座標 \(Q_\alpha\) を特定するには 2 つの実数が必要であるが, 全体では \(N\) 個の独立な実数が有ればよい [1][A]. \(q_j(t)\) が実数であることに注意して, 式 (8-77) の複素共役をとると次が言えるからである： \begin{equation} Q_\alpha^{\,*}=\reverse{\sqrt{N}}\sum_{j=1}^{N} … Continue reading．
実数座標を用いたいならば, 以下のような 2 つの実数 \(Q_{\alpha}^{\,C},\,Q_{\alpha}^{\,S}\) を座標とすればよい：
\begin{align}
&Q_{\alpha}=\reverse{\sqrt{2}}\bigl(Q_{\alpha}^{C}-iQ_{\alpha}^{S}\bigr),\qquad
Q_{\alpha}Q_{\alpha}^{*}=\half\left[\bigl(Q_{\alpha}^{C}\bigr)^{2}+\bigl(Q_{\alpha}^{S}\bigr)^{2}\right]
\tag{8-79}\\
&Q_{\alpha}^{C}=\reverse{\sqrt{2}}\bigl(Q_{\alpha}+Q_{-\alpha}\bigr),\qquad
Q_{\alpha}^{S}=\frac{i}{\sqrt{2}}\bigl(Q_{\alpha}-Q_{-\alpha}\bigr)
\tag{8-80}
\end{align}

このとき \(Q_{\alpha}^{\,C}\), \(Q_{\alpha}^{\,S}\) の　\(\alpha\) の値は \(0\) から \(\displaystyle{\frac{1}{2}(N-1)}\) までとなる． ( \(\alpha=0\) は並進運動に相当したので, 運動エネルギーも考えるときは \(\alpha=0\) を必ず含めなければならないからであろう?!)． 運動エネルギーの項を実数座標で表わすならば式 (8-53)： \(\displaystyle{T=\reverse{2}\sum_{\alpha=0}^{N-1}\dot{Q}_{\alpha}^{\,2}}\) となるのだった．そこで「 \(Q_{\alpha}^{\,C}\) と \(Q_{\alpha}^{\,S}\) を一緒にしたものがこの実数座標である」と見做すならば, 運動エネルギー \(T\) の項は式 (8-79) を利用して次となる：
\begin{align}
T&=\half \sum_{\alpha=0}^{N-1}\dot{Q}_{\alpha}^{*}\dot{Q}_{\alpha}
=\half \sum_{\alpha=-\half(N-1)}^{\half(N-1)}\dot{Q}_{\alpha}^{*}\dot{Q}_{\alpha}\notag\\
&=\half \sum_{\alpha=0}^{\half(N-1)}\dot{Q}_{-\alpha}\dot{Q}_{-\alpha}^{*}
+\half \sum_{\alpha=0}^{\half(N-1)}\dot{Q}_{\alpha}^{*}\dot{Q}_{\alpha}\notag\\
&=\sum_{\alpha=0}^{\half(N-1)}\dot{Q}_{\alpha}^{*}\dot{Q}_{\alpha}\notag\\
&=\sum_{\alpha=0}^{\half(N-1)}\half\Big[\big(\dot{Q}_{\alpha}^{C}\big)^{2}
+\big(\dot{Q}_{\alpha}^{S}\big)^{2}\Big]
=\half \sum_{\alpha=0}^{\half(N-1)}\Big[\big(\dot{Q}_{\alpha}^{C}\big)^{2}
+\big(\dot{Q}_{\alpha}^{S}\big)^{2}\Big]
\tag{8-81}
\end{align}

[ 式 (8-78) には 因子 \(\frac{1}{2}\) が再び現れている．これが必要なのは， \(\alpha\) の範囲を\(\alpha=0\sim N-1\) ではなくて, 式 (8-78′) のように \(\alpha=-\frac{1}{2}(N-1)\sim \frac{1}{2}(N-1)\) までとした場合 \(\alpha\) の正負の全ての値について和をとると \(Q_{-\alpha}^{\,*}Q_{-\alpha}=Q_{\alpha}Q_{\alpha}^{\,*}\) であるので,[2]式 (8-80) より, \begin{equation} Q_{-\alpha}^{\ C}=\reverse{\sqrt{2}}(Q_{-\alpha}+Q_{\alpha})=Q_{\alpha}^{\ C},\quad\mathrm{and}\quad Q_{-\alpha}^{\ … Continue reading それぞれの項を 2 度数えることになるからである]．
よって, 以前に求めた実数量に対する 2 次形式, 例えば式 (8-67) は, ここでは 1 つの複素数にその複素共役を掛け合わせたものの和の形となる．

———————————————————————————————————————————————

References

References
↑1 [A]. \(q_j(t)\) が実数であることに注意して, 式 (8-77) の複素共役をとると次が言えるからである：
\begin{equation}
Q_\alpha^{\,*}=\reverse{\sqrt{N}}\sum_{j=1}^{N} q_j^{*}(t)e^{i2\pi\alpha j/N}
=\reverse{\sqrt{N}}\sum_{j=1}^{N} q_j(t)e^{-i2\pi(-\alpha)j/N}=Q_{-\alpha}
\tag{1}
\end{equation}

従って, 例えば \(\alpha\) が奇数であり, \(N\) を偶数として \(\alpha=-\frac{1}{2}(N-1)\sim \frac{1}{2}(N-1)\) の \((N+1)\) 個であるとすると, \(\alpha\) はゼロと \(\alpha=1\sim \frac{1}{2}(N-1)\) の \(\frac{1}{2}(N-1)\) 個でよい．ゼロ以外の各 \(\alpha\) に対する \(Q_\alpha\) を特定するには 2 つの実数が必要であるから, 結局 \(1+2\times \frac{1}{2}(N-1)=N\) 個の独立な実数が必要だと言える．

[B]. 変位 \(q_j(t)=\sum_{\alpha} c_\alpha a_{j\alpha}^{*}\,e^{-i\omega_\alpha t}\) に於いて, ある一つの \(\alpha\) の基準振動だけがゼロでないとすると, \(q_j\) は式 (8-71) の形に表され, 振動数は全ての \(j\) に共通な \(\omega_\alpha\) を持つが, 振幅は位置 \(j\) ごとに違う \(a_{j\alpha}\) を持つ：

\begin{equation}
q_j=\sum_{\alpha} c_\alpha a_{j\alpha}^{*}\,e^{-i\omega_\alpha t}=a_{j\alpha}^{*}e^{-i\omega_{\alpha} t}=\frac{1}{\sqrt{N}}e^{iK_{\alpha} j}\,e^{-i\omega_{\alpha} t}
= \frac{1}{\sqrt{N}}e^{i(K_{\alpha} j-\omega_{\alpha} t)}=Q_{\alpha}
\tag{2}
\end{equation}

この式の形から,『基準振動 \(Q_{\alpha}\) は, 角波数 \(K_\alpha=2\pi\alpha/(N b)\) を持つ「進行波」である』と言える．ただし \(b\) は格子間隔とする．

[C]. テル・ハールによれば,『基準座標 \(Q_\alpha\) の代わりに, \(Q_\alpha^{\ C}\) と \(Q_\alpha^{\ S}\) を使って基準モードを記述するとき, 上記の進行波に代わって「定常波」を得ることが出来る』．それを示すには, 前述の結果式 (2) から \(Q_{-\alpha}\) を求め, それから式 (8-80) を用いて \(Q_{\alpha}^{\ C}\) と \(Q_{\alpha}^{\ C}\) を書いてみるとよい．

\begin{equation}
Q_{\alpha}=Ae^{i(K_\alpha j -\omega_\alpha t)},\qquad Q_{-\alpha}=Ae^{i(-K_\alpha j -\omega_\alpha t)}
\tag{3}
\end{equation}

従って,
\begin{align}
Q_{\alpha}^{\ C}&= \frac{1}{\sqrt{2}}\Big( Q_{\alpha}+Q_{-\alpha}\Big)
=\frac{A}{\sqrt{2}}e^{-i\omega_{\alpha}t}\Big( e^{iK_{\alpha}j} + e^{-iK_{\alpha}j} \Big)\notag\\
&= \sqrt{2}\,Ae^{-i\omega_{\alpha}t}\cos(K_{\alpha}j),
\tag{4}
\end{align}

\begin{align}
Q_{\alpha}^{\ S}&= \frac{i}{\sqrt{2}}\Big( Q_{\alpha}-Q_{-\alpha} \Big)
=\frac{iA}{\sqrt{2}}e^{-i\omega_{\alpha}t}\Big( e^{iK_{\alpha}j} – e^{-iK_{\alpha}j} \Big)\notag\\
&= -\sqrt{2}\,Ae^{-i\omega_{\alpha}t}\sin(K_{\alpha}j)
\tag{5}
\end{align}

これらは何方も,「時間 \(t\) 依存性と位置 \(j\) 依存性とは分離されている」．従って, これらの波動は「定常波である」と言える．
↑2 式 (8-80) より,
\begin{equation}
Q_{-\alpha}^{\ C}=\reverse{\sqrt{2}}(Q_{-\alpha}+Q_{\alpha})=Q_{\alpha}^{\ C},\quad\mathrm{and}\quad
Q_{-\alpha}^{\ S}=\frac{i}{\sqrt{2}}(Q_{-\alpha}-Q_{\alpha})=-Q_{\alpha}^{\ S}
\tag{6}
\end{equation}

が言える．従って,
\begin{align}
Q_{-\alpha}^{\,*}Q_{-\alpha}&=\reverse{\sqrt{2}}\left(Q_{-\alpha}^{C}+iQ_{-\alpha}^{S}\right)\times
\reverse{\sqrt{2}}\left(Q_{-\alpha}^{C}-iQ_{-\alpha}^{S}\right)\notag\\
&=\reverse{\sqrt{2}}\left(Q_{\alpha}^{C}-iQ_{\alpha}^{S}\right)\times\reverse{\sqrt{2}}
\left(Q_{\alpha}^{C}+iQ_{\alpha}^{S}\right)\notag\\
&=Q_{\alpha}Q_{\alpha}^{*}
\tag{7}
\end{align}