
\(\)
Problem 6-8
In an atom the potential follows the Coulomb law only for very small radii. As the radius is increased the atomic electrons gradually shield, or cancel out, the nuclear charge until, for sufficiently large values of \(r\), the potential is zero. The shielding effect of atomic electrons can be accounted for in a very rough approximate manner with the formula
\begin{equation}
V(r)=-\frac{Z e^{2}}{r} e^{-r/a}
\tag{6-51}
\end{equation}
V(r)=-\frac{Z e^{2}}{r} e^{-r/a}
\tag{6-51}
\end{equation}
In this expression \(a\) is called the radius of the atom. It is not the same as the outer radius of the atom as used by chemists, but instead is given by \(a_0/Z^{1/3}\), where \(a_0\) is the Bohr radius and \(a_0=\hbar^{2}/m e^{2}=0.0529\) nm.
Show that in such a potential
\begin{equation}
v(q)=-\frac{4\pi Z e^{2} \hbar^{2}}{q^{2}+(\hbar/a)^{2}}
\tag{6-52}
\end{equation}
v(q)=-\frac{4\pi Z e^{2} \hbar^{2}}{q^{2}+(\hbar/a)^{2}}
\tag{6-52}
\end{equation}
and hence
\begin{equation}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\frac{d \sigma}{d\Omega}=\frac{Z^{2}e^{4}}{\ds{\left(\frac{m u^{2}}{2}\right)^{2}\left(4\sin^{2}\frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}}\right)^{2}}}
\tag{6-53}
\end{equation}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\frac{d \sigma}{d\Omega}=\frac{Z^{2}e^{4}}{\ds{\left(\frac{m u^{2}}{2}\right)^{2}\left(4\sin^{2}\frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}}\right)^{2}}}
\tag{6-53}
\end{equation}
The total cross section \(\sigma_{T}\) is defined as the integral of \(d\sigma/d\Omega\) of over the unit sphere; thus
\begin{equation}
\sigma_{T}=\int_{0}^{4\pi} \frac{d\sigma}{d\Omega}\,d\Omega
\tag{6-54}
\end{equation}
\sigma_{T}=\int_{0}^{4\pi} \frac{d\sigma}{d\Omega}\,d\Omega
\tag{6-54}
\end{equation}
In the present example show that \(\sigma_{T}\) is given by
\begin{equation}
\sigma_{T}=\pi a^{2}\frac{4Z^{2}e^{4}/(u \hbar)^{2}}{1+\hbar^{2}/(2p a)^{2}}
\tag{6-55}
\end{equation}
\sigma_{T}=\pi a^{2}\frac{4Z^{2}e^{4}/(u \hbar)^{2}}{1+\hbar^{2}/(2p a)^{2}}
\tag{6-55}
\end{equation}
( 解答 ) 問題 6-6 で得られた結果式 (6-45) 中の \(V(r)\) に, 式 (6-51) を代入すると,
\begin{align}
v(q)&=\frac{4\pi\hbar}{q}\int_0^{\infty}dr\,r\,\sin\left(\frac{q}{\hbar}r\right)\,V(r)\\
&=\frac{4\pi\hbar}{q}\int_0^{\infty}dr\,r\,\sin\left(\frac{q}{\hbar}r\right)\times\left(-\frac{Ze^{2}}{r}e^{-r/a}\right)\\
&=-\frac{4\pi\hbar Ze^{2}}{q}\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr
\tag{1}
\end{align}
v(q)&=\frac{4\pi\hbar}{q}\int_0^{\infty}dr\,r\,\sin\left(\frac{q}{\hbar}r\right)\,V(r)\\
&=\frac{4\pi\hbar}{q}\int_0^{\infty}dr\,r\,\sin\left(\frac{q}{\hbar}r\right)\times\left(-\frac{Ze^{2}}{r}e^{-r/a}\right)\\
&=-\frac{4\pi\hbar Ze^{2}}{q}\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr
\tag{1}
\end{align}
このときの積分部分 \(I_1\) は, 部分積分法を用いると,
\begin{align}
I_1&=\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr\\
&=-\frac{\hbar}{q}\left[\cos\left(\frac{q}{\hbar}r\right)e^{-r/a}\right]_0^{\infty}+\frac{\hbar}{q}
\times\left(-\frac{1}{a}\right)\int_0^{\infty}\cos\left(\frac{q}{\hbar}r\right)e^{-r/a}\,dr\\
&=\frac{\hbar}{q}-\frac{\hbar}{qa}\int_0^{\infty}e^{-r/a}\,\cos\left(\frac{q}{\hbar}r\right)\,dr
\tag{2}
\end{align}
I_1&=\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr\\
&=-\frac{\hbar}{q}\left[\cos\left(\frac{q}{\hbar}r\right)e^{-r/a}\right]_0^{\infty}+\frac{\hbar}{q}
\times\left(-\frac{1}{a}\right)\int_0^{\infty}\cos\left(\frac{q}{\hbar}r\right)e^{-r/a}\,dr\\
&=\frac{\hbar}{q}-\frac{\hbar}{qa}\int_0^{\infty}e^{-r/a}\,\cos\left(\frac{q}{\hbar}r\right)\,dr
\tag{2}
\end{align}
この式中の積分を \(I_2\) とするならば,それはやはり部分積分法を用いて,
\begin{align}
I_2&=\int_0^{\infty}e^{-r/a}\,\cos\left(\frac{q}{\hbar}r\right)\,dr\\
&=\frac{\hbar}{q}\left[\sin\left(\frac{q}{\hbar}r\right)e^{-r/a}\right]_0^{\infty}-\frac{\hbar}{q}\times\left(-\frac{1}{a}\right)
\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr\\
&=\frac{\hbar}{aq}\,I_1
\tag{3}
\end{align}
I_2&=\int_0^{\infty}e^{-r/a}\,\cos\left(\frac{q}{\hbar}r\right)\,dr\\
&=\frac{\hbar}{q}\left[\sin\left(\frac{q}{\hbar}r\right)e^{-r/a}\right]_0^{\infty}-\frac{\hbar}{q}\times\left(-\frac{1}{a}\right)
\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr\\
&=\frac{\hbar}{aq}\,I_1
\tag{3}
\end{align}
以上から,
\begin{equation}
I_1=\frac{\hbar}{q}-\frac{\hbar}{qa}\times\frac{\hbar}{aq}\,I_1,\ \rightarrow\
I_1=\frac{\hbar a^{2}q}{\hbar^{2}+a^{2}q^{2}}=\frac{\hbar q}{q^{2}+(\hbar/a)^{2}}
\tag{4}
\end{equation}
I_1=\frac{\hbar}{q}-\frac{\hbar}{qa}\times\frac{\hbar}{aq}\,I_1,\ \rightarrow\
I_1=\frac{\hbar a^{2}q}{\hbar^{2}+a^{2}q^{2}}=\frac{\hbar q}{q^{2}+(\hbar/a)^{2}}
\tag{4}
\end{equation}
従って式 (1) は次に書ける:
\begin{align}
v(q)&=-\frac{4\pi\hbar Ze^{2}}{q}\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr\\
&=-\frac{4\pi\hbar Ze^{2}}{q}\times\frac{\hbar q}{q^{2}+(\hbar/a)^{2}}\\
&=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}+(\hbar/a)^{2}}
\tag{5}
\end{align}
v(q)&=-\frac{4\pi\hbar Ze^{2}}{q}\int_0^{\infty}e^{-r/a}\,\sin\left(\frac{q}{\hbar}r\right)\,dr\\
&=-\frac{4\pi\hbar Ze^{2}}{q}\times\frac{\hbar q}{q^{2}+(\hbar/a)^{2}}\\
&=-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}+(\hbar/a)^{2}}
\tag{5}
\end{align}
この結果を式 (6-44) に代入し, \(q=2p\sin(\theta/2)=2mu\sin(\theta/2)\) であることを用いると, 散乱断面積
\begin{equation}
\def\mb#1{\mathbf{#1}}
I=\frac{d\sigma(\theta)}{d\Omega}=\left(\frac{m}{2\pi\hbar^{2}}\right)^{2}\bigl|v(\mb{q})\bigr|^{2}
\end{equation}
\def\mb#1{\mathbf{#1}}
I=\frac{d\sigma(\theta)}{d\Omega}=\left(\frac{m}{2\pi\hbar^{2}}\right)^{2}\bigl|v(\mb{q})\bigr|^{2}
\end{equation}
は次となる:
\begin{align}
I&=\left(\frac{m}{2\pi\hbar^{2}}\right)^{2}\left|-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}+(\hbar/a)^{2}}\right|^{2}\\
&=\frac{m^{2}}{4\pi^{2}\hbar^{4}}\times 16\pi^{2}Z^{2}e^{4}\hbar^{4}\left\{4p^{2}\sin^{2}\frac{\theta}{2}
+\frac{\hbar^{2}}{a^{2}}\right\}^{-2}\\
&=4m^{2}Z^{2}e^{4} \left[ p^{2}\left\{ 4\sin^{2} \frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}}\right\}\right]^{-2}\\
&=Z^{2}e^{4} \left[ \frac{m^{2}u^{2}}{2m} \left\{ 4\sin^{2}\frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}} \right\} \right]^{-2}\\
&=\frac{Z^{2} e^{4}}{\ds{\left(\frac{mu^{2}}{2}\right)^{2}\left[ 4\sin^{2}\frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}} \right]^{2}}}
\tag{6}
\end{align}
I&=\left(\frac{m}{2\pi\hbar^{2}}\right)^{2}\left|-\frac{4\pi\hbar^{2}Ze^{2}}{q^{2}+(\hbar/a)^{2}}\right|^{2}\\
&=\frac{m^{2}}{4\pi^{2}\hbar^{4}}\times 16\pi^{2}Z^{2}e^{4}\hbar^{4}\left\{4p^{2}\sin^{2}\frac{\theta}{2}
+\frac{\hbar^{2}}{a^{2}}\right\}^{-2}\\
&=4m^{2}Z^{2}e^{4} \left[ p^{2}\left\{ 4\sin^{2} \frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}}\right\}\right]^{-2}\\
&=Z^{2}e^{4} \left[ \frac{m^{2}u^{2}}{2m} \left\{ 4\sin^{2}\frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}} \right\} \right]^{-2}\\
&=\frac{Z^{2} e^{4}}{\ds{\left(\frac{mu^{2}}{2}\right)^{2}\left[ 4\sin^{2}\frac{\theta}{2}+\frac{\hbar^{2}}{(p a)^{2}} \right]^{2}}}
\tag{6}
\end{align}
このとき, 上式は Rutherford 散乱の断面積の式 (6-46) に較べて, 分母の因子 \(4\sin^{2}(\theta/2)\) に余分な因子 \(\hbar^{2}/(p a)^{2}\) が付加された形になっていることに注意する.
単位球上での微小立体角 \(d\Omega\) は \(d\Omega=2\pi\sin\theta d\theta\) である (下図 1 を参照).従って, 式 (6-53) の単位立体角上の積分を, 方向角 \(\theta\) による積分に変換するならば次となる:
\begin{equation}
I_T=\sigma_T=\int_0^{4\pi} \frac{d\sigma}{d\Omega}\,d\Omega=\int_0^{\pi}\frac{d\sigma(\theta)}{d\Omega}\,2\pi\sin\theta\,d\theta
\end{equation}
I_T=\sigma_T=\int_0^{4\pi} \frac{d\sigma}{d\Omega}\,d\Omega=\int_0^{\pi}\frac{d\sigma(\theta)}{d\Omega}\,2\pi\sin\theta\,d\theta
\end{equation}
よって,
\begin{align}
I_T &=\int_0^{\pi} \frac{Z^{2} e^{4}2\pi\sin\theta}{\ds{\left(\frac{mu^{2}}{2}\right)^{2}\left[ 4\sin^{2}\frac{\theta}{2}
+\frac{\hbar^{2}}{(p a)^{2}} \right]^{2}}}\,d\theta\\
&=\frac{4Z^{2}e^{4}}{(mu^{2})^{2}}\int_0^{\pi} \frac{2\pi\sin\theta\,d\theta}{\ds{\left[ 2(1-\cos\theta)
+\frac{\hbar^{2}}{(p a)^{2}}\right]^{2}}}
\tag{7}
\end{align}
I_T &=\int_0^{\pi} \frac{Z^{2} e^{4}2\pi\sin\theta}{\ds{\left(\frac{mu^{2}}{2}\right)^{2}\left[ 4\sin^{2}\frac{\theta}{2}
+\frac{\hbar^{2}}{(p a)^{2}} \right]^{2}}}\,d\theta\\
&=\frac{4Z^{2}e^{4}}{(mu^{2})^{2}}\int_0^{\pi} \frac{2\pi\sin\theta\,d\theta}{\ds{\left[ 2(1-\cos\theta)
+\frac{\hbar^{2}}{(p a)^{2}}\right]^{2}}}
\tag{7}
\end{align}
ここでさらに \(t=\cos\theta\) の変数変換を行ない, \(B = \hbar^{2}/(p a)^{2}\) と置くならば, 求めるべき式 (6-55)が次のように得られる:
\begin{align}
I_T &=\frac{4Z^{2}e^{4}}{(mu^{2})^{2}}\int_{-1}^{1}\frac{2\pi\,dt}{\Bigl[2(1-t)+B\Bigr]^{2}}
=\frac{4Z^{2}e^{4}}{(mu^{2})^{2}}\frac{4\pi}{B(B+4)}\\
&=\pi a^{2}\frac{4Z^{2}e^{4}/(u\hbar)^{2}}{1+\hbar^{2}/(2pa)^{2}}
\tag{8}
\end{align}
I_T &=\frac{4Z^{2}e^{4}}{(mu^{2})^{2}}\int_{-1}^{1}\frac{2\pi\,dt}{\Bigl[2(1-t)+B\Bigr]^{2}}
=\frac{4Z^{2}e^{4}}{(mu^{2})^{2}}\frac{4\pi}{B(B+4)}\\
&=\pi a^{2}\frac{4Z^{2}e^{4}/(u\hbar)^{2}}{1+\hbar^{2}/(2pa)^{2}}
\tag{8}
\end{align}
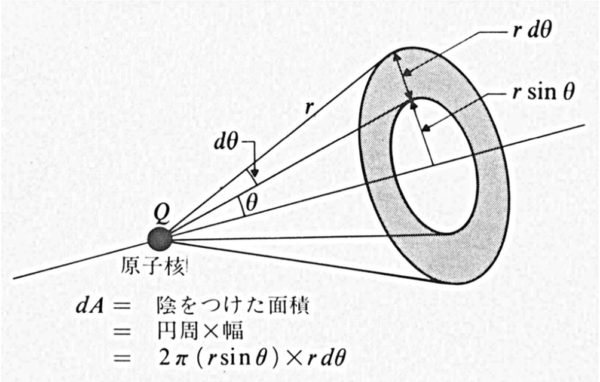
図 1. 陰を付けた面積は円周×幅として, \(dS=2\pi\times r\sin\theta\times r d\theta\) である.従って, それに対する立体角は \(d\Omega=dS/r^{2}=2\pi\sin\theta\,d\theta\) となる.
( 参考 ) 式 (6-52) は, D.Bohm : 「QUANTUM THEORY」 の第 21 章「応用例 : 遮蔽された Coulomb 力」の式 (34a) と等価である.ただし, 散乱を起させる粒子の電荷を \(Z_1\) とし散乱される方の粒子の電荷を \(Z_2\) として, 遮蔽されたクーロンポテンシャルは次としている:
\begin{equation}
V=\frac{Z_1 Z_2 e^{2}}{r}\exp\left(-\frac{r}{r_0}\right)
\tag{34}
\end{equation}
V=\frac{Z_1 Z_2 e^{2}}{r}\exp\left(-\frac{r}{r_0}\right)
\tag{34}
\end{equation}
よって \(Z_1=Z\), \(Z_2=-1\), \(r_0=a\) とすれば, 式(6-52) に一致する訳である.そして \(v(q)\) に等価な表現である \(V(\mb{k}-\mb{k}_0)\) では, \(q=\hbar (\mb{k}-\mb{k}_0)\) に相当している.問題 5. で,「この \(V(\mb{k}-\mb{k}_0)\) を求めよ」となっている.それには p.618 の式 (38a) 中に式 (34) の \(V(r)\) を代入してやればよいので次となる:
\begin{align}
&V(\mb{k}-\mb{k}_0)=\frac{2\pi}{i|\mb{k}-\mb{k}_0|}\int_0^{\infty} V(r)\big( e^{i|\mb{k}-\mb{k}_0|r}-e^{-i|\mb{k}-\mb{k}_0|r} \big)\,r\,dr \tag{38a}\\
&=\frac{2\pi}{i|\mb{k}-\mb{k}_0|}\int \frac{Z_1 Z_2 e^{2}}{r}\exp\left(-\frac{r}{r_0}\right)\big(e^{i|\mb{k}-\mb{k}_0|r}
-e^{-i|\mb{k}-\mb{k}_0|r} \big)\,r\,dr\\
&=\frac{2\pi}{i|\mb{k}-\mb{k}_0|}Z_1 Z_2 e^{2}\int_0^{\infty} \exp\left(-\frac{r}{r_0}\right)\times
2i\sin(|\mb{k}-\mb{k}_0|r)\,dr\\
&=\frac{4\pi Z_1 Z_2 e^{2}}{|\mb{k}-\mb{k}_0|}\int_0^{\infty} \exp\left(-\frac{r}{r_0}\right) \sin(|\mb{k}-\mb{k}_0|r)\,dr\\
&=\frac{4\pi Z_1 Z_2 e^{2}}{|\mb{k}-\mb{k}_0|^{2}+(1/r_0)^{2}}
\tag{34a}
\end{align}
&V(\mb{k}-\mb{k}_0)=\frac{2\pi}{i|\mb{k}-\mb{k}_0|}\int_0^{\infty} V(r)\big( e^{i|\mb{k}-\mb{k}_0|r}-e^{-i|\mb{k}-\mb{k}_0|r} \big)\,r\,dr \tag{38a}\\
&=\frac{2\pi}{i|\mb{k}-\mb{k}_0|}\int \frac{Z_1 Z_2 e^{2}}{r}\exp\left(-\frac{r}{r_0}\right)\big(e^{i|\mb{k}-\mb{k}_0|r}
-e^{-i|\mb{k}-\mb{k}_0|r} \big)\,r\,dr\\
&=\frac{2\pi}{i|\mb{k}-\mb{k}_0|}Z_1 Z_2 e^{2}\int_0^{\infty} \exp\left(-\frac{r}{r_0}\right)\times
2i\sin(|\mb{k}-\mb{k}_0|r)\,dr\\
&=\frac{4\pi Z_1 Z_2 e^{2}}{|\mb{k}-\mb{k}_0|}\int_0^{\infty} \exp\left(-\frac{r}{r_0}\right) \sin(|\mb{k}-\mb{k}_0|r)\,dr\\
&=\frac{4\pi Z_1 Z_2 e^{2}}{|\mb{k}-\mb{k}_0|^{2}+(1/r_0)^{2}}
\tag{34a}
\end{align}
また, 1977年の第 8 刷の本では, 式 (34) の下にある式が,
\begin{equation}
V(\mb{k}-\mb{k}_0)=Z_1 Z_2 e^{2}\int \exp\left(-\frac{r}{r_0}\right)\exp\frac{[i(\mb{k}-\mb{k}_0)\cdot\mb{p}]d\mb{p}}{r}
\end{equation}
V(\mb{k}-\mb{k}_0)=Z_1 Z_2 e^{2}\int \exp\left(-\frac{r}{r_0}\right)\exp\frac{[i(\mb{k}-\mb{k}_0)\cdot\mb{p}]d\mb{p}}{r}
\end{equation}
となっている.しかし, これは明らかに印刷ミスではなかろうか?. (D. ボーム:「量子論」は, 新装版が2019年に出版されているようである.そちらがどうなっているかは確認していない.)

