
\(\)
Problem 6-13
Assume \(V(\mathbf{r},t)\) is actually independent of \(t\). Substituting for the free-particle kernel \(K_{0}\) in Eq.(6-61), integrate the result over \(t\) to show that
\begin{equation}
\def\mb#1{\mathbf{#1}}
\psi(\mb{R}_{b},t_{b})= e^{-(i/\hbar)E_{a} t_{b}}\left[ e^{(i/\hbar)\mb{p}_{a}\cdot\mb{R}_{b}}
+ \frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,\frac{1}{r_{b c}}e^{(i/\hbar) p r_{b c}} V(\mb{r}_{c}) e^{(i/\hbar)\mb{p}_{a}\cdot\mb{r}_{c}}\right]
\tag{6-62}
\end{equation}
\def\mb#1{\mathbf{#1}}
\psi(\mb{R}_{b},t_{b})= e^{-(i/\hbar)E_{a} t_{b}}\left[ e^{(i/\hbar)\mb{p}_{a}\cdot\mb{R}_{b}}
+ \frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,\frac{1}{r_{b c}}e^{(i/\hbar) p r_{b c}} V(\mb{r}_{c}) e^{(i/\hbar)\mb{p}_{a}\cdot\mb{r}_{c}}\right]
\tag{6-62}
\end{equation}
where \(r_{b c}\) is the distance from the final point \(b\) to the variable point of integration \(c\) and \(p\) is the magnitude of the momentum of the electron.
Once more, suppose that the potential drops to \(0\) for distances which are short compared to either \(R_{a}\) or \(R_{b}\). Show that Eq.(6-62) can be written as
\begin{equation}
\psi(\mb{R}_{b},t_{b})=e^{(i/\hbar)E_{b} t_{b}} e^{(i/\hbar)\mb{p}_{a}\cdot\mb{R}_{b}}
+ f(\mb{q})\frac{e^{(i/\hbar) p R_{b}}}{R_{b}}
\tag{6-63}
\end{equation}
\psi(\mb{R}_{b},t_{b})=e^{(i/\hbar)E_{b} t_{b}} e^{(i/\hbar)\mb{p}_{a}\cdot\mb{R}_{b}}
+ f(\mb{q})\frac{e^{(i/\hbar) p R_{b}}}{R_{b}}
\tag{6-63}
\end{equation}
where the scattering amplitude \(f(\mb{q})\) is defined in terms of \(v(\mb{q})\) [ see Eq.(6-39) ] as
\begin{align}
f(\mb{q}) &=-\frac{m}{2\pi\hbar^{2}}v(\mb{q}),\tag{6-64}\\
\mathrm{where}&\quad v(\mb{q})=\int d^{3}\mb{r}\,e^{i\mb{q}\cdot\mb{r}/\hbar}V(\mb{r}),\qquad \mb{q}=\mb{p}_{a}-\mb{p}_{b}
\notag
\end{align}
f(\mb{q}) &=-\frac{m}{2\pi\hbar^{2}}v(\mb{q}),\tag{6-64}\\
\mathrm{where}&\quad v(\mb{q})=\int d^{3}\mb{r}\,e^{i\mb{q}\cdot\mb{r}/\hbar}V(\mb{r}),\qquad \mb{q}=\mb{p}_{a}-\mb{p}_{b}
\notag
\end{align}
The last term of Eq.(6-63), \(f(\mb{q})\,e^{I p R_{b}/\hbar}/R_{b}\), can be thought of as the spatial part of the scattered wave function. It has the form of a spherical wave radiating outward from the center of the scattering atom. The amplitude of this spherical wave at some particular scattering angle depends upon that angle through the function \(f(\mb{q})\), which, by Eq.(6-64), varies with the momentum transfer \(\mb{q}\). Thus the complete wave functions for the electrons after scattering can be thought of as the sum of two terms. The first term is the plane wave of nonscattered electrons, \(e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}\), and the second term is the spherical wave of scattered electrons, as indicated in Fig.6-10. Use this point of view to derive the formula for the cross section \(d\sigma/d\Omega\).
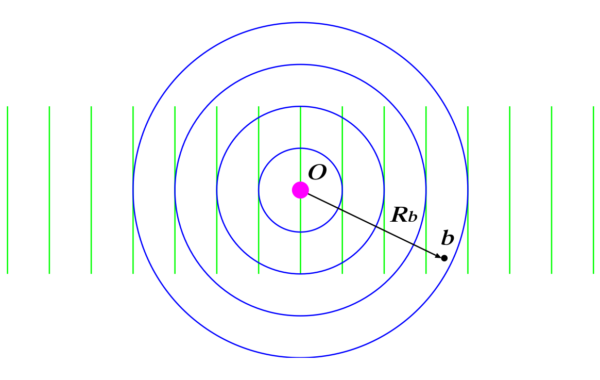
Fig. 6-10. a beam of electrons, represented by its equivalent wave, moves toward the atomic nucleus at \(0\). The strongest fraction of beam moves on undisturbed as a plane wave with momentum \(\mb{p}_{a}\). A small fraction of the beam is scattered from the atomic nucleus and moves away from \(O\) as a spherical wave pattern. The resulting strength of the wave of electrons (the number of electrons) at some point \(b\) located at \(\mb{R}_{b}\) measured from the atomic nucleus \(0\), is then made up of two parts. The first is the nonscattered beam given by the plane wave \(e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}\). To this is added the scattered wave with the spherical form given by \(e^{i p R_{b}/\hbar}/R_{b}\) and multiplied by the function \(f(\mb{q})\), which determines the angular dependence. The combination of these two waves gives the spherical part of the scattered wave function.
( 解答例 ) 原書では式(6-62)の [ ]が抜けている. また, 式(6-64)では \(f(\mb{q})\) に負符号が付いていない. しかし J.J.Sakurai の式と一致させるためにマイナス符号を付けたので注意する. Emended Edition by D.F.Styer では負符号がキチンと付いている.
式(6.61) において \(V(\mb{r},t_{c})=V(\mb{r}_{c})\) とし, また \(K_{0}\) として, 問題4-12 で求めた次の3次元自由粒子核
\begin{equation}
K_{0}=\left(\frac{m}{2\pi i\hbar(t_{b}-t_{c})}\right)^{3/2}\exp\left[\frac{i m (\mb{R}_{b}-\mb{r}_{c})^{2}}{2\hbar(t_{b}-t_{c})}\right]
\tag{1}
\end{equation}
K_{0}=\left(\frac{m}{2\pi i\hbar(t_{b}-t_{c})}\right)^{3/2}\exp\left[\frac{i m (\mb{R}_{b}-\mb{r}_{c})^{2}}{2\hbar(t_{b}-t_{c})}\right]
\tag{1}
\end{equation}
を用いるならば, 式(6-61)から次式が得られる :
\begin{align}
\psi(\mb{R}_{b},t_{b})&= e^{i\mb{p}_{a}\cdot\mb{R}_{b} – i E_{a} t_{b}/\hbar}
-\frac{i}{\hbar}\int_{0}^{t_{b}} dt_{c}\int d^{3}\mb{r}_{c}\,K_{0}(\mb{R}_{b},t_{b};\mb{r}_{c},t_{c})\,V(\mb{r})
\,e^{i\mb{p}_{a}\cdot\mb{r}/\hbar}\,e^{-i E_{a} t_{c}/\hbar}\notag\\
&=e^{i\mb{p}_{a}\cdot\mb{R}_{b}-i E_{a} t_{b}/\hbar}
-\frac{i}{\hbar}\int_{0}^{t_{b}}dt_{c}\int d^{3}\mb{r}_{c}\,\left(\frac{m}{2\pi i\hbar(t_{b}-t_{c})}\right)^{3/2}
\exp\left[\frac{i m (\mb{R}_{b}-\mb{r}_{c})^{2}}{2\hbar(t_{b}-t_{c})}\right]\,V(\mb{r}_{c})
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,e^{-i E_{a} t_{c}/\hbar}
\tag{2}
\end{align}
\psi(\mb{R}_{b},t_{b})&= e^{i\mb{p}_{a}\cdot\mb{R}_{b} – i E_{a} t_{b}/\hbar}
-\frac{i}{\hbar}\int_{0}^{t_{b}} dt_{c}\int d^{3}\mb{r}_{c}\,K_{0}(\mb{R}_{b},t_{b};\mb{r}_{c},t_{c})\,V(\mb{r})
\,e^{i\mb{p}_{a}\cdot\mb{r}/\hbar}\,e^{-i E_{a} t_{c}/\hbar}\notag\\
&=e^{i\mb{p}_{a}\cdot\mb{R}_{b}-i E_{a} t_{b}/\hbar}
-\frac{i}{\hbar}\int_{0}^{t_{b}}dt_{c}\int d^{3}\mb{r}_{c}\,\left(\frac{m}{2\pi i\hbar(t_{b}-t_{c})}\right)^{3/2}
\exp\left[\frac{i m (\mb{R}_{b}-\mb{r}_{c})^{2}}{2\hbar(t_{b}-t_{c})}\right]\,V(\mb{r}_{c})
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,e^{-i E_{a} t_{c}/\hbar}
\tag{2}
\end{align}
この第2項目を \(I\) とし, これだけを考える. \((\mb{R}_{b}-\mb{r}_{c})=r_{b c}\) とおくと次となる:
\begin{align}
I&=-\frac{i}{\hbar}\left(\frac{m}{2\pi i\hbar}\right)^{3/2}\int_{0}^{t_{b}}dt_{c}\int d^{3}\mb{r}_{c}\,
(t_{b}-t_{c})^{-3/2}\exp\left[\frac{i m r_{b c}^{2}}{2\hbar (t_{b}-t_{c})}\right]\,V(\mb{r}_{c})
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,e^{-i E_{a} t_{c}/\hbar}\\
&=-\frac{m}{2\pi\hbar^{2}}\left(\frac{m}{2\pi i\hbar}\right)^{1/2}\int d^{3}\mb{r}_{c}
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,V(\mb{r}_{c})\int_{0}^{t_{b}} dt_{c}\,(t_{b}-t_{c})^{-3/2}
\exp\left[\frac{i m r_{b c}^{\ 2}}{2\hbar(t_{b}-t_{c})}\right]\,e^{-i E_{a} t_{c}/\hbar}
\tag{3}
\end{align}
I&=-\frac{i}{\hbar}\left(\frac{m}{2\pi i\hbar}\right)^{3/2}\int_{0}^{t_{b}}dt_{c}\int d^{3}\mb{r}_{c}\,
(t_{b}-t_{c})^{-3/2}\exp\left[\frac{i m r_{b c}^{2}}{2\hbar (t_{b}-t_{c})}\right]\,V(\mb{r}_{c})
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,e^{-i E_{a} t_{c}/\hbar}\\
&=-\frac{m}{2\pi\hbar^{2}}\left(\frac{m}{2\pi i\hbar}\right)^{1/2}\int d^{3}\mb{r}_{c}
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,V(\mb{r}_{c})\int_{0}^{t_{b}} dt_{c}\,(t_{b}-t_{c})^{-3/2}
\exp\left[\frac{i m r_{b c}^{\ 2}}{2\hbar(t_{b}-t_{c})}\right]\,e^{-i E_{a} t_{c}/\hbar}
\tag{3}
\end{align}
さらにこの内の時間積分 \(I_{1}\) だけを取り出して考える:
\begin{align}
I_{1}&=\int_{0}^{t_{b}}dt_{c}\,(t_{b}-t_{c})^{-3/2}\exp\left[\frac{i m r_{b c}^{\ 2}}{2\hbar (t_{b}-t_{c})}\right]
\,e^{i E_{a}(t_{b}-t_{c}-t_{b})/\hbar}\\
&=e^{-i E_{a}t_{b}/\hbar}\int_{0}^{t_{b}} dt_{c}\,(t_{b}-t_{c})^{-3/2}\exp\left[\frac{i m r_{b c}^{\ 2}}{2\hbar(t_{b}-t_{c})}
+\frac{i E_{a}}{\hbar}(t_{b}-t_{c})\right]
\tag{4}
\end{align}
I_{1}&=\int_{0}^{t_{b}}dt_{c}\,(t_{b}-t_{c})^{-3/2}\exp\left[\frac{i m r_{b c}^{\ 2}}{2\hbar (t_{b}-t_{c})}\right]
\,e^{i E_{a}(t_{b}-t_{c}-t_{b})/\hbar}\\
&=e^{-i E_{a}t_{b}/\hbar}\int_{0}^{t_{b}} dt_{c}\,(t_{b}-t_{c})^{-3/2}\exp\left[\frac{i m r_{b c}^{\ 2}}{2\hbar(t_{b}-t_{c})}
+\frac{i E_{a}}{\hbar}(t_{b}-t_{c})\right]
\tag{4}
\end{align}
ここで \((t_{b}-t_{c})^{-1/2}=y\) と置くと, \((t_{b}-t_{c})^{-3/2}dt=2dy\) で積分範囲は \([1/\sqrt{t_{b}},\infty]\) であるが \(t_{b}\) は十分に大きな時間であるとするならば \(1/\sqrt{t_{b}}\simeq 0\) と近似してよかろう. すると,
\begin{equation}
I_{1}\simeq e^{-i E_{a} t_{b}/\hbar}\, 2\int_{0}^{\infty}dy\,
\exp\left[\frac{i m r_{bc}^{\ 2}}{2\hbar}y^{2}+i\frac{E_{a}}{\hbar}\frac{1}{y^{2}}\right]
\tag{5}
\end{equation}
I_{1}\simeq e^{-i E_{a} t_{b}/\hbar}\, 2\int_{0}^{\infty}dy\,
\exp\left[\frac{i m r_{bc}^{\ 2}}{2\hbar}y^{2}+i\frac{E_{a}}{\hbar}\frac{1}{y^{2}}\right]
\tag{5}
\end{equation}
巻末の「役に立つ積分」から次の公式を利用する :
\begin{equation}
\int_{0}^{\infty}\exp\left\{\frac{i a}{x^{2}}+i b x^{2}\right\}\,dx=\sqrt{\frac{i\pi}{4b}}\exp\Big[i 2\sqrt{a b}\Big]
\tag{A-3}
\end{equation}
\int_{0}^{\infty}\exp\left\{\frac{i a}{x^{2}}+i b x^{2}\right\}\,dx=\sqrt{\frac{i\pi}{4b}}\exp\Big[i 2\sqrt{a b}\Big]
\tag{A-3}
\end{equation}
この場合, \(a=E_{a}/\hbar\), \(b=m r_{bc}^{\ 2}\,/2\hbar\) である. また \(E_{a}=p^{2}/2m\) を用いる. すると積分 \(I_{1}\) は次となる:
\begin{equation}
I_{1}=2\, e^{-i E_{a} t_{b}/\hbar}\sqrt{\frac{i\pi}{4}\frac{2\hbar}{m r_{b c}^{\ 2}}}
\exp\left\{i2\sqrt{\frac{m E_{a} r_{b c}^{\ 2}}{2\hbar^{2}}}\right\}
=2\,e^{-i E_{a} t_{b}/\hbar}\frac{1}{r_{b c}}\sqrt{\frac{i\pi\hbar}{2m}}\,\exp\left[\frac{i p r_{bc}}{\hbar}\right]
\tag{6}
\end{equation}
I_{1}=2\, e^{-i E_{a} t_{b}/\hbar}\sqrt{\frac{i\pi}{4}\frac{2\hbar}{m r_{b c}^{\ 2}}}
\exp\left\{i2\sqrt{\frac{m E_{a} r_{b c}^{\ 2}}{2\hbar^{2}}}\right\}
=2\,e^{-i E_{a} t_{b}/\hbar}\frac{1}{r_{b c}}\sqrt{\frac{i\pi\hbar}{2m}}\,\exp\left[\frac{i p r_{bc}}{\hbar}\right]
\tag{6}
\end{equation}
従って式(3)の \(I\) は次となる:
\begin{align}
I&=-\frac{m}{2\pi\hbar^{2}}\left(\frac{m}{2\pi i\hbar}\right)^{1/2}\int d^{3}\mb{r}_{c}\,
e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,V(\mb{r}_{c})\,2\,e^{-i E_{a} t_{b}/\hbar}\frac{1}{r_{bc}}
\left(\frac{i\pi\hbar}{2m}\right)^{1/2}\,\exp\left[\frac{i p r_{bc}}{\hbar}\right]\\
&=-e^{-i E_{a} t_{b}/\hbar}\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,
\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}V(\mb{r}_{c})\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}
\tag{7}
\end{align}
I&=-\frac{m}{2\pi\hbar^{2}}\left(\frac{m}{2\pi i\hbar}\right)^{1/2}\int d^{3}\mb{r}_{c}\,
e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\,V(\mb{r}_{c})\,2\,e^{-i E_{a} t_{b}/\hbar}\frac{1}{r_{bc}}
\left(\frac{i\pi\hbar}{2m}\right)^{1/2}\,\exp\left[\frac{i p r_{bc}}{\hbar}\right]\\
&=-e^{-i E_{a} t_{b}/\hbar}\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,
\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}V(\mb{r}_{c})\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}
\tag{7}
\end{align}
この結果式(7)より, 式(2)の \(\psi(\mb{R}_{b},t_{b})\) は最終的に次のように書くことが出来る:
\begin{align}
\psi(\mb{R}_{b},t_{b})&=e^{i\mb{p}_{a}\cdot\mb{R}_{b}-i E_{a} t_{b}/\hbar}-e^{-i E_{a} t_{b}/\hbar}\frac{m}{2\pi\hbar^{2}}
\int d^{3}\mb{r}_{c}\,\frac{e^{i p r_{bc}/\hbar}}{r_{b c}}V(\mb{r}_{c})\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\\
&=e^{-i E_{a} t_{b}/\hbar}\left[e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}-\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}
\,\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}V(\mb{r}_{c})\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\right]
\tag{8}
\end{align}
\psi(\mb{R}_{b},t_{b})&=e^{i\mb{p}_{a}\cdot\mb{R}_{b}-i E_{a} t_{b}/\hbar}-e^{-i E_{a} t_{b}/\hbar}\frac{m}{2\pi\hbar^{2}}
\int d^{3}\mb{r}_{c}\,\frac{e^{i p r_{bc}/\hbar}}{r_{b c}}V(\mb{r}_{c})\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\\
&=e^{-i E_{a} t_{b}/\hbar}\left[e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}-\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}
\,\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}V(\mb{r}_{c})\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}\right]
\tag{8}
\end{align}
次にポテンシャルが影響を与える領域 \(\mb{r}_{c}\) が \(R_{a},R_{b}\) に比べて非常に小さい場合を考える. このとき前と同様に, \(r_{b c}\simeq R_{b}-\mb{i}_{b}\cdot\mb{r}_{c}\simeq R_{b}\) として近似するならば,
\begin{align}
\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}\simeq \frac{1}{R_{b}-\mb{i}_{b}\cdot\mb{r}_{c}}\exp\left[
\frac{ip\,(R_{b}-\mb{i}_{b}\cdot\mb{r}_{c})}{\hbar}\right]
\simeq \frac{1}{R_{b}}\exp\left[i\frac{p R_{b}}{\hbar}-i\frac{\mb{p}_{b}\cdot\mb{r}_{c}}{\hbar}\right]
\end{align}
\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}\simeq \frac{1}{R_{b}-\mb{i}_{b}\cdot\mb{r}_{c}}\exp\left[
\frac{ip\,(R_{b}-\mb{i}_{b}\cdot\mb{r}_{c})}{\hbar}\right]
\simeq \frac{1}{R_{b}}\exp\left[i\frac{p R_{b}}{\hbar}-i\frac{\mb{p}_{b}\cdot\mb{r}_{c}}{\hbar}\right]
\end{align}
従って, 式 (8) の第 2 項は次のように書ける:
\begin{align}
-\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}V(\mb{r}_{c})
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}
&\simeq -\frac{m}{2\pi\hbar^{2}}\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}\,e^{i\mb{p}_{a}\cdot
\mb{r}_{c}/\hbar}\,e^{-i\mb{p}_{b}\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})\\
&=-\frac{m}{2\pi\hbar^{2}}\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}
\,e^{i(\mb{p}_{a}-\mb{p}_{b})\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})\\
&=-\frac{m}{2\pi\hbar^{2}}\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}\,e^{i\mb{q}\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})
\tag{9}
\end{align}
-\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,\frac{e^{i p r_{b c}/\hbar}}{r_{b c}}V(\mb{r}_{c})
\,e^{i\mb{p}_{a}\cdot\mb{r}_{c}/\hbar}
&\simeq -\frac{m}{2\pi\hbar^{2}}\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}\,e^{i\mb{p}_{a}\cdot
\mb{r}_{c}/\hbar}\,e^{-i\mb{p}_{b}\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})\\
&=-\frac{m}{2\pi\hbar^{2}}\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}
\,e^{i(\mb{p}_{a}-\mb{p}_{b})\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})\\
&=-\frac{m}{2\pi\hbar^{2}}\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}\,e^{i\mb{q}\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})
\tag{9}
\end{align}
よって, 式(6-62) は次のように近似した表現式とすることが出来る:
\begin{align}
\psi(\mb{R}_{b},t_{b})&\simeq e^{-i E_{b} t_{b}/\hbar}\left[e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}-\frac{m}{2\pi\hbar^{2}}
\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}\,e^{i\mb{q}\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})\right]\\
&=e^{-i E_{b} t_{b}/\hbar}\left[e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}+\frac{e^{i p R_{b}/\hbar}}{R_{b}}\,f(\mb{q})\right],\\
\quad \mathrm{where}&\quad f(\mb{q})=-\frac{m}{2\pi\hbar^{2}}v(\mb{q})
=-\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,e^{i\mb{q}\cdot\mb{r}_{c}/\hbar}\,V(\mb{r}_{c})
\tag{10}
\end{align}
\psi(\mb{R}_{b},t_{b})&\simeq e^{-i E_{b} t_{b}/\hbar}\left[e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}-\frac{m}{2\pi\hbar^{2}}
\frac{e^{i p R_{b}/\hbar}}{R_{b}}\int d^{3}\mb{r}_{c}\,e^{i\mb{q}\cdot\mb{r}_{c}/\hbar}V(\mb{r}_{c})\right]\\
&=e^{-i E_{b} t_{b}/\hbar}\left[e^{i\mb{p}_{a}\cdot\mb{R}_{b}/\hbar}+\frac{e^{i p R_{b}/\hbar}}{R_{b}}\,f(\mb{q})\right],\\
\quad \mathrm{where}&\quad f(\mb{q})=-\frac{m}{2\pi\hbar^{2}}v(\mb{q})
=-\frac{m}{2\pi\hbar^{2}}\int d^{3}\mb{r}_{c}\,e^{i\mb{q}\cdot\mb{r}_{c}/\hbar}\,V(\mb{r}_{c})
\tag{10}
\end{align}
最後に, 微分断面積は式(6-44) から求めることが出来る :
\begin{equation}
\frac{d\sigma}{d\Omega}=\big| f(\mb{q}) \big|^{2}=\left|-\frac{m}{2\pi\hbar^{2}}v(\mb{q})\right|^{2}
\tag{11}
\end{equation}
\frac{d\sigma}{d\Omega}=\big| f(\mb{q}) \big|^{2}=\left|-\frac{m}{2\pi\hbar^{2}}v(\mb{q})\right|^{2}
\tag{11}
\end{equation}


