\(\)
Problem 6-2
Suppose a system consists of two particles which interact only through a potential \(V(x,y)\), where \(x\) represents the coordinates of the first particle and \(y\) represents the coordinates of the second [cf. Sec. 3-8 and Eq. (3-75) ]. Apart from this interaction, the particles are free. If \(V\) were \(0\), then \(K\) would be simply a product of the two free-particle kernels. Using this fact, develop a perturbation expansion for \(K_V(x_b,y_b, t_b ; x_a, y_a, t_a)\). By what rules of physical reasoning can the various terms in this expression be described ?
(解答) 式 (3.75)を参照して, この場合の核を書くならば次となる：
\begin{equation}
K_V(b,a)=\int_a^{b}\mathscr{D}x(t)\int_a^{b}\mathscr{D}y(t)\,\exp\left[\frac{i}{\hbar}\int_{t_a}^{t_b}
dt\,\left\{\frac{m}{2}\dot{x}^{2}+\frac{M}{2}\dot{y}^{2}-V(x,y)\right\}\right]
\tag{1}
\end{equation}
K_V(b,a)=\int_a^{b}\mathscr{D}x(t)\int_a^{b}\mathscr{D}y(t)\,\exp\left[\frac{i}{\hbar}\int_{t_a}^{t_b}
dt\,\left\{\frac{m}{2}\dot{x}^{2}+\frac{M}{2}\dot{y}^{2}-V(x,y)\right\}\right]
\tag{1}
\end{equation}
これをまず経路 \(y(t)\) について積分するならば, 形式的に次のように書ける：
\begin{equation}
K_V(b,a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right)T_V\big[x(t)\big],
\tag{2}
\end{equation}
K_V(b,a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right)T_V\big[x(t)\big],
\tag{2}
\end{equation}
ただし,
\begin{equation}
T_{V}\bigl[x(t)\bigr]=\int_a^{b}\mathscr{D}y(t)\exp\left[\frac{i}{\hbar}
\int_{t_a}^{t_b}dt\,\left\{\frac{M}{2}\dot{y}^{2}-V(x,y)\right\}\right]
\tag{3}
\end{equation}
T_{V}\bigl[x(t)\bigr]=\int_a^{b}\mathscr{D}y(t)\exp\left[\frac{i}{\hbar}
\int_{t_a}^{t_b}dt\,\left\{\frac{M}{2}\dot{y}^{2}-V(x,y)\right\}\right]
\tag{3}
\end{equation}
このとき式 (3) で定義された汎関数 \(T_{V}\big[x(t)\big]\) は, ポテンシャル \(V(x,y)\) の影響下で第 2 粒子のみが端点 \(y_a,\,\,y_b\) の間を動く振幅 \(T_{V}(b,a)\) である．
このときポテンシャル \(V(x,y)\) が小さければ， \(V(x,y)\) は式 (6.3) と同様に級数展開できる：
\begin{equation}
\exp\left[-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,y)\right]
=1-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,y)+\frac{1}{2!}\left(\frac{i}{\hbar}\right)^{2}\left[
\int_{t_a}^{t_b}dt\,V(x,y)\right]^{2}+\dotsb
\tag{4}
\end{equation}
\exp\left[-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,y)\right]
=1-\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,V(x,y)+\frac{1}{2!}\left(\frac{i}{\hbar}\right)^{2}\left[
\int_{t_a}^{t_b}dt\,V(x,y)\right]^{2}+\dotsb
\tag{4}
\end{equation}
この展開を式 (3) に代入すれば, 振幅 \(T_V(b,a)\) は次のように書ける：
\begin{equation}
T_{V}(b,a)=T_{V}\big[x(t)\big]=T_{0}(b,a)+T^{(1)}(b,a)+T^{(2)}(b,a)+\dotsb
\label{5}
\end{equation}
T_{V}(b,a)=T_{V}\big[x(t)\big]=T_{0}(b,a)+T^{(1)}(b,a)+T^{(2)}(b,a)+\dotsb
\label{5}
\end{equation}
ただし各項は次である：
\begin{align}
T_0(b,a)&=\int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right),\tag{6}\\
T^{(1)}(b,a)&=-\frac{i}{\hbar}\int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}
\int_{t_{a}}^{t_{b}}dt\,\frac{M}{2}\dot{y}^{2}\right)\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr],\tag{7}\\
T^{(2)}(b,a)&=-\frac{1}{2\hbar^{2}}\int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}
\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right)
\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr]\int_{t_a}^{t_b}ds^{‘}\,V\bigl[x(s^{‘}),y(s^{‘})\bigr]
\tag{8}
\end{align}
T_0(b,a)&=\int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right),\tag{6}\\
T^{(1)}(b,a)&=-\frac{i}{\hbar}\int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}
\int_{t_{a}}^{t_{b}}dt\,\frac{M}{2}\dot{y}^{2}\right)\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr],\tag{7}\\
T^{(2)}(b,a)&=-\frac{1}{2\hbar^{2}}\int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}
\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right)
\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr]\int_{t_a}^{t_b}ds^{‘}\,V\bigl[x(s^{‘}),y(s^{‘})\bigr]
\tag{8}
\end{align}
すると, 式 (2) の \(K_V(b,a)\) は次のように書ける：
\begin{align}
&K_V(b,a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right)\left(T_{0}(b,a)+T^{(1)}(b,a)+T^{(2)}(b,a)+\dotsb\right)\\
&=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right)
T_0(b,a)+\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}
\right)T^{(1)}(b,a)\\
&\qquad+\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right)T^{(2)}(b,a)+\dotsb
\end{align}
&K_V(b,a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right)\left(T_{0}(b,a)+T^{(1)}(b,a)+T^{(2)}(b,a)+\dotsb\right)\\
&=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right)
T_0(b,a)+\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}
\right)T^{(1)}(b,a)\\
&\qquad+\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right)T^{(2)}(b,a)+\dotsb
\end{align}
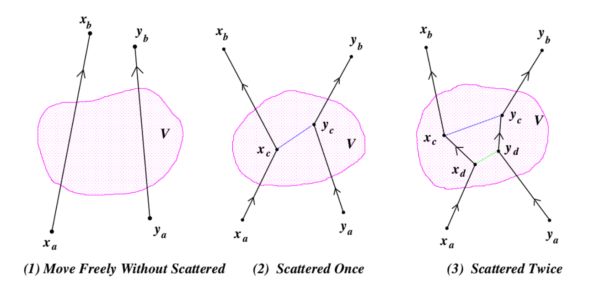
この第 1 項は, 第 1 粒子と第 2 粒子が相互作用せず自由に運動する場合の振幅である：
\begin{align}
&K_0(x_b,y_b,t_b;x_a,y_a,t_a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,
\frac{m}{2}\dot{x}^{2}\right)T_{0}(b,a)\\
&=\int_a^{b}\mathscr{D}x(t)\,\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right) \int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right)\\
&\rightarrow\ K_0(b,a)=K_0(x_b,t_b;x_a,t_a)\,K_0(y_b,t_b;y_a,t_a)
\tag{9}
\end{align}
&K_0(x_b,y_b,t_b;x_a,y_a,t_a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,
\frac{m}{2}\dot{x}^{2}\right)T_{0}(b,a)\\
&=\int_a^{b}\mathscr{D}x(t)\,\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right) \int_a^{b}\mathscr{D}y(t)\,\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right)\\
&\rightarrow\ K_0(b,a)=K_0(x_b,t_b;x_a,t_a)\,K_0(y_b,t_b;y_a,t_a)
\tag{9}
\end{align}
第 2 項は, 単一散乱 (一度だけ相互作用 \(V(x_c,y_c)\) をする) の振幅 \(K^{(1)}(b,a)\) である：
\begin{align}
&K^{(1)}(b,a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right)T^{(1)}(b,a)\\
&=\int_a^{b}\mathscr{D}x(t)\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right\}\left(-\frac{i}{\hbar}\right)\int_a^{b}\mathscr{D}y(t)\exp\left\{\frac{i}{\hbar}
\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right\}\\
&\qquad\times\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr]\\
&=-\frac{i}{\hbar}\int_{t_a}^{t_b}dt_c\int_{-\infty}^{\infty}dx_c\,K_0(b,c)\,V[x_c,y_c]\,K_0(c,a)
\tag{10}
\end{align}
&K^{(1)}(b,a)=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right)T^{(1)}(b,a)\\
&=\int_a^{b}\mathscr{D}x(t)\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right\}\left(-\frac{i}{\hbar}\right)\int_a^{b}\mathscr{D}y(t)\exp\left\{\frac{i}{\hbar}
\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right\}\\
&\qquad\times\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr]\\
&=-\frac{i}{\hbar}\int_{t_a}^{t_b}dt_c\int_{-\infty}^{\infty}dx_c\,K_0(b,c)\,V[x_c,y_c]\,K_0(c,a)
\tag{10}
\end{align}
第 3 項は 2 重散乱の振幅, すなわち 2 粒子は位置 \(d\) で相互作用 \(V[x_d,y_d]\) を行なった後, 自由運動して行き, 再び位置 \(c\) で 2 回めの相互作用 \(V[x_c,y_c]\) を行い, その後は互いに自由運動して去って行く振幅である：
\begin{align}
K^{(2)}(b,a)&=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right)T^{(2)}(b,a)\\
&=\int_a^{b}\mathscr{D}x(t)\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right\}
\left(-\frac{1}{2\hbar^{2}}\right)\int_a^{b}\mathscr{D}y(t)\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right\}\\
&\qquad\times\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr]\int_{t_a}^{t_b}ds^{‘}\,V\bigl[x(s^{‘}),y(s^{‘})\bigr]\\
&=\left(-\frac{i}{\hbar}\right)^{2}\int d\tau_c\int d\tau_d\,K_0(b,c)\,V[x_c,y_c]\,K_0(c,d)\,V[x_d,y_d]\,K_0(d,a)
\tag{11}
\end{align}
K^{(2)}(b,a)&=\int_a^{b}\mathscr{D}x(t)\exp\left(\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}
\dot{x}^{2}\right)T^{(2)}(b,a)\\
&=\int_a^{b}\mathscr{D}x(t)\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{m}{2}\dot{x}^{2}\right\}
\left(-\frac{1}{2\hbar^{2}}\right)\int_a^{b}\mathscr{D}y(t)\exp\left\{\frac{i}{\hbar}\int_{t_a}^{t_b}dt\,\frac{M}{2}\dot{y}^{2}\right\}\\
&\qquad\times\int_{t_a}^{t_b}ds\,V\bigl[x(s),y(s)\bigr]\int_{t_a}^{t_b}ds^{‘}\,V\bigl[x(s^{‘}),y(s^{‘})\bigr]\\
&=\left(-\frac{i}{\hbar}\right)^{2}\int d\tau_c\int d\tau_d\,K_0(b,c)\,V[x_c,y_c]\,K_0(c,d)\,V[x_d,y_d]\,K_0(d,a)
\tag{11}
\end{align}
ただし \(d\tau_c=dx_c dt_c\) 及び \(d\tau_d=dx_d dt_d\) である．
以上の各項をまとめて書くならば, 次のような摂動展開をしたことになる：
\begin{equation}
K_V(b,a)=K_0(b,a)+K^{(1)}(b,a)+K^{(2)}(b,a)+\dotsb
\tag{12}
\end{equation}
K_V(b,a)=K_0(b,a)+K^{(1)}(b,a)+K^{(2)}(b,a)+\dotsb
\tag{12}
\end{equation}
この摂動展開の物理的な意味は下図 1. を参照して欲しい．
図 1. (1) では, 第 1 粒子と第 2 粒子は相互作用せずに自由に運動する．(2) では, 各々が自由粒子の運動をして来て, 位置 \(x_c\) と \(y_c\) で相互作用 \(V(x_c,y_c)\) をした (散乱) 後, 自由粒子として去って行く．(3) では, 各粒子は位置 \((x_d,y_d)\) と \((x_c,y_c)\) で相互作用 \(V(x_d,y_d)\) 及び \(V(x_c,y_c)\) を受けて 2 回の散乱をした後で, 自由粒子として去って行く．
