\(\)
Problem 7-7
Show that for any quadratic action
\begin{equation}
\langle x(t) \rangle = \bar{x}(t)\langle 1 \rangle
\tag{7-57}
\end{equation}
\langle x(t) \rangle = \bar{x}(t)\langle 1 \rangle
\tag{7-57}
\end{equation}
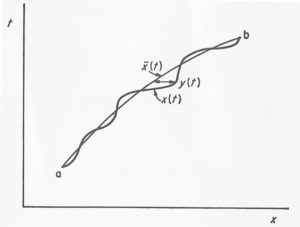
( 解答 ) § 3-5 の議論にあるように, 指定された端点 \(a,\,b\) 間の古典軌道を \(\bar{x}(t)\) とし, 変数 \(x\) を古典軌道 \(\bar{x}(t)\) とそれからのズレ \(y(t)\) を用いて \(x(t)=\bar{x}(t)+y(t)\) と表現する(下図 1. を参照).
このとき \(dx_i=dy_i\) かつ \(\mathscr{D}x(t)=\mathscr{D}y(t)\) であり, さらに端点は固定することが暗黙の了解になっているので \(y(t_b)=y(t_a)=0\) である.すると, 遷移要素の定義式 (7-3) から
\begin{align}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
&\BraKet{\chi}{x(t)}{\psi}_S=\BraKet{\chi}{\bar{x}(t)+y(t)}{\psi}_S\\
&\quad =\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\int_a^{b} \mathscr{D}x(t)\,\chi^{*}(x_b)
\,\bigl\{\bar{x}(t)+y(t)\bigr\}\,e^{iS/\hbar}\,\psi(x_a)\\
&\quad=\int dx_b\int dx_a\int_{a}^{b} \mathscr{D}x(t)\,\chi^{*}(x_b)\,\bar{x}(t)\,e^{iS/\hbar}\,\psi(x_a)\\
&\qquad +\int dx_b\int dx_a\int_0^{0} \mathscr{D}y(t)\,\chi^{*}(x_b)\,y(t)\,e^{iS/\hbar}\,\psi(x_a)
\tag{1}
\end{align}
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
&\BraKet{\chi}{x(t)}{\psi}_S=\BraKet{\chi}{\bar{x}(t)+y(t)}{\psi}_S\\
&\quad =\int_{-\infty}^{\infty} dx_b\int_{-\infty}^{\infty} dx_a\int_a^{b} \mathscr{D}x(t)\,\chi^{*}(x_b)
\,\bigl\{\bar{x}(t)+y(t)\bigr\}\,e^{iS/\hbar}\,\psi(x_a)\\
&\quad=\int dx_b\int dx_a\int_{a}^{b} \mathscr{D}x(t)\,\chi^{*}(x_b)\,\bar{x}(t)\,e^{iS/\hbar}\,\psi(x_a)\\
&\qquad +\int dx_b\int dx_a\int_0^{0} \mathscr{D}y(t)\,\chi^{*}(x_b)\,y(t)\,e^{iS/\hbar}\,\psi(x_a)
\tag{1}
\end{align}
このとき, § 3-5「ガウス積分」での議論により,「作用が 2 次式である場合には, \(y\) の1次の項の積分はゼロになるべき」である.よって, 上式の第 2 項はゼロであるから,
\begin{align}
\langle x(t) \rangle=\BraKet{\chi}{x(t)}{\psi}_S &=\int dx_b\int dx_a\int_{x_a}^{x_b} \mathscr{D}x(t)\,\chi^{*}(x_b)\,\bar{x}(t)\,e^{iS/\hbar}\,\psi(x_a)\\
&=\BraKet{\chi}{\bar{x}(t)}{\psi}_S=\langle \bar{x}(t)\rangle
\tag{2}
\end{align}
\langle x(t) \rangle=\BraKet{\chi}{x(t)}{\psi}_S &=\int dx_b\int dx_a\int_{x_a}^{x_b} \mathscr{D}x(t)\,\chi^{*}(x_b)\,\bar{x}(t)\,e^{iS/\hbar}\,\psi(x_a)\\
&=\BraKet{\chi}{\bar{x}(t)}{\psi}_S=\langle \bar{x}(t)\rangle
\tag{2}
\end{align}
さらに, この古典的経路 \(\bar{x}(t)\) は決まった経路で経路積分には依存しない量である.従って \(\bar{x}(t)\) は積分の外へ出せる:
\begin{align}
\langle x(t) \rangle=\BraKet{\chi}{\bar{x}(t)}{\psi}_S
&=\int dx_b\int dx_a\int_{x_a}^{x_b} \mathscr{D}x(t)\,\chi^{*}(x_b)\,\bar{x}(t)\,e^{iS/\hbar}\,\psi(x_a)\\
&=\bar{x}(t)\int dx_2\int dx_1\int_a^{b} \mathscr{D}x(t)\,\chi^{*}(x_2)\,e^{iS/\hbar}\,\psi(x_1)\\
&=\bar{x}(t)\BraKet{\chi}{1}{\psi}_S=\bar{x}(t)\,\langle\, 1 \,\rangle
\tag{3}
\end{align}
\langle x(t) \rangle=\BraKet{\chi}{\bar{x}(t)}{\psi}_S
&=\int dx_b\int dx_a\int_{x_a}^{x_b} \mathscr{D}x(t)\,\chi^{*}(x_b)\,\bar{x}(t)\,e^{iS/\hbar}\,\psi(x_a)\\
&=\bar{x}(t)\int dx_2\int dx_1\int_a^{b} \mathscr{D}x(t)\,\chi^{*}(x_2)\,e^{iS/\hbar}\,\psi(x_1)\\
&=\bar{x}(t)\BraKet{\chi}{1}{\psi}_S=\bar{x}(t)\,\langle\, 1 \,\rangle
\tag{3}
\end{align}
よって, ラグランジアン \(L\) が2次関数で作用 \(S\) が2次形式となる場合には, 式 (7-57) が成り立つと言える:
\begin{equation}
\langle x(t) \rangle=\langle \bar{x}(t)+y(t) \rangle=\langle \bar{x}(t) \rangle=\bar{x}(t)\,\langle\,1\,\rangle
\tag{4}
\end{equation}
\langle x(t) \rangle=\langle \bar{x}(t)+y(t) \rangle=\langle \bar{x}(t) \rangle=\bar{x}(t)\,\langle\,1\,\rangle
\tag{4}
\end{equation}