\(\)
J.D.ジャクソンの電磁気学§11.4から「相対論的なドップラー効果」について, そして J.B.ハートルの「重力」§5.5から「相対論的ビーミング」についての文章を抜粋し, それに多少の補足を与えたものを示す．
相対論的なドップラー効果
相対論的な Doppler 効果の公式は, 光波の位相が不変量であることから導くことが出来る．Lorentz 変換の下では, どんな平面波でもその位相は不変である．位相は, 座標系には無関係な計数の操作に関連するからである．座標系 \(K\) で,振動数 \(\omega\),波数ベクトル \(\def\mb#1{\mathbf{#1}}\mb{k}\) の平面波を考える．座標 \(\mb{x}\) の点 \(P\) の観測者が, ある時間内に到達する波頭の数を記録する装置を持っているとする．観測者は \(t=0\) で原点を通過した波頭を (観測者の所まで来た時) 第１番目の波頭と記録する場合, その観測者は時刻 \(t\) までに次の個数の波頭を計測する：
\begin{equation}
N=\frac{1}{2\pi}(\omega t -\mb{k}\cdot\mb{x})
\tag{1}
\end{equation}
N=\frac{1}{2\pi}(\omega t -\mb{k}\cdot\mb{x})
\tag{1}
\end{equation}
なぜなら, 波動の式 \(f(x)=A\sin(\omega t -kx)\) に於いて, 位相 \(\omega t-kx\) を \(2\pi\) で割った量が時間 \(t\) の間に通過した波頭の数 \(N\) になるからである．
いま, 系 \(K\) に対して \(z\)-軸の方向に速度 \(\mb{v}\) で運動している別の座標系 \(K’\) を考える．\(t=0\) で, 系 \(K’\) の原点は系 \(K\) の原点と一致していたとする．系 \(K’\) では座標 \(\mb{x}’\) の点 \(P’\) で, 観測者が系 \(K\) の観測者と同じ装置を持っている．この観測者は, 原点を通過した波頭が観測点 \(P’\) まで到達した瞬間から波頭の数を計数し始めて, 時刻 \(t’\) まで計数を続ける．計数を終了した瞬間に \(P’\) の位置が点 \(P\) と一致する場合, 両観測者が記録した波頭の数は等しい．すると, 系 \(K’\) での平面波の波動ベクトルと振動数を \(\mb{k}’\) 及び \(\omega’\) とするならば, 系 \(K’\) の観測者は次の個数の波頭を数えたはずである：
\begin{equation}
N=\frac{1}{2\pi}(\omega’ t’-\mb{k}’\cdot\mb{x}’)
\tag{2}
\end{equation}
N=\frac{1}{2\pi}(\omega’ t’-\mb{k}’\cdot\mb{x}’)
\tag{2}
\end{equation}
すなわち, 波の位相は不変である．従って, 式 (1) と式 (2) から次が得られる：
\begin{equation}
\omega t-\mb{k}\cdot\mb{x}=\omega’t’-\mb{k}’\cdot\mb{x}’
\tag{3}
\end{equation}
\omega t-\mb{k}\cdot\mb{x}=\omega’t’-\mb{k}’\cdot\mb{x}’
\tag{3}
\end{equation}
この式は, ４-位置ベクトル \(x^{\mu}\) と ４-波数ベクトル \(k^{\mu}\) のスカラー積 \(k^{\mu}x_{\mu}\) の不変性を表した式になっている．これは, ４次元の波数ベクトルを \(k^{\mu}=(\omega/c,\mb{k})\) としてよいことを示している．
そこで, ４-ベクトル \((A_0,A_1,A_2,A_3)\) のローレンツ変換公式
\begin{equation}
A’_{0}=\gamma(A_0-\mb{\beta}\cdot\mb{A}),\quad A’_{\parallel}=\gamma(A_{\parallel}-\beta A_0),\quad
\mb{A}’_{\perp}=\mb{A}_{\perp}
\tag{4}
\end{equation}
A’_{0}=\gamma(A_0-\mb{\beta}\cdot\mb{A}),\quad A’_{\parallel}=\gamma(A_{\parallel}-\beta A_0),\quad
\mb{A}’_{\perp}=\mb{A}_{\perp}
\tag{4}
\end{equation}
を用いるならば, ４-波数ベクトル \(k^{\mu}\) の \(k’^{\mu}\) への変換は次のように表される：
\begin{equation}
k’_{0}=\gamma(k_{0}-\mb{\beta}\cdot\mb{k}),\quad k’_{\parallel}=\gamma(k_{\parallel}-\mb{\beta}k_{0}),\quad
\mb{k}’_{\perp}=\mb{k}_{\perp}
\tag{5}
\end{equation}
k’_{0}=\gamma(k_{0}-\mb{\beta}\cdot\mb{k}),\quad k’_{\parallel}=\gamma(k_{\parallel}-\mb{\beta}k_{0}),\quad
\mb{k}’_{\perp}=\mb{k}_{\perp}
\tag{5}
\end{equation}
光波の場合は \(k=|\mb{k}|=k_{0}\) で \(\omega=ck=ck_{0}\) であるから \(k_{0}=\omega/c\) である．よって, この場合は次となる：
\begin{align}
&k’_{0}=\frac{\omega’}{c}=\gamma\left(\frac{\omega}{c}-\frac{v}{c}k_z\right)
\quad\rightarrow\quad \omega’=\gamma(\omega-vk_z),\notag\\
&k’_z=\gamma\left(k_z-\frac{v}{c}\frac{\omega}{c}\right)=\gamma\left(k_z-\frac{v}{c^{2}}\omega\right),\quad
k’_x=k_x,\quad k’_y=k_y
\tag{6}
\end{align}
&k’_{0}=\frac{\omega’}{c}=\gamma\left(\frac{\omega}{c}-\frac{v}{c}k_z\right)
\quad\rightarrow\quad \omega’=\gamma(\omega-vk_z),\notag\\
&k’_z=\gamma\left(k_z-\frac{v}{c}\frac{\omega}{c}\right)=\gamma\left(k_z-\frac{v}{c^{2}}\omega\right),\quad
k’_x=k_x,\quad k’_y=k_y
\tag{6}
\end{align}
更に, 波の伝搬方向も表している波数ベクトル \(\mb{k}\) が, 系 \(K’\) の移動速度 \(\mb{v}\) と成す角度を \(\theta\) とするならば,
\begin{equation}
k_z=k\cos\theta=\frac{\omega}{c}\cos\theta,\quad \tan\theta=\frac{\mb{k}_{\perp}}{k_{\parallel}}
\tag{7}
\end{equation}
k_z=k\cos\theta=\frac{\omega}{c}\cos\theta,\quad \tan\theta=\frac{\mb{k}_{\perp}}{k_{\parallel}}
\tag{7}
\end{equation}
これを上式 (6) の \(\omega’\) に代入すると,
\begin{align}
\omega’&=\gamma(\omega-vk_z)=\gamma\left(\omega-v\frac{\omega}{c}\cos\theta\right)
=\gamma\omega\left(1-\frac{v}{c}\cos\theta\right)\notag\\
&=\gamma\omega(1-\beta\cos\theta)
\tag{8}
\end{align}
\omega’&=\gamma(\omega-vk_z)=\gamma\left(\omega-v\frac{\omega}{c}\cos\theta\right)
=\gamma\omega\left(1-\frac{v}{c}\cos\theta\right)\notag\\
&=\gamma\omega(1-\beta\cos\theta)
\tag{8}
\end{align}
また, 系 \(K’\) から見た波数 \(\mb{k}’\) と系 \(K’\) の移動速度 \(\mb{v}\) との成す角度を \(\theta’\) とするならば, 式 (5) を用いて次が言える：
\begin{align}
\tan\theta’&=\frac{\mb{k}’_{\perp}}{k’_{\parallel}}=\frac{\mb{k}_{\perp}}{\gamma(k_{\parallel}-\mb{\beta} k_0)}
=\frac{\mb{k}_{\perp}/k_{\parallel}}{\gamma(1-\mb{\beta} k_0/k_{\parallel})}
=\frac{\tan\theta}{\gamma(1-\beta/\cos\theta)}\notag\\
&=\frac{\sin\theta}{\gamma(\cos\theta-\beta)}
\tag{9}
\end{align}
\tan\theta’&=\frac{\mb{k}’_{\perp}}{k’_{\parallel}}=\frac{\mb{k}_{\perp}}{\gamma(k_{\parallel}-\mb{\beta} k_0)}
=\frac{\mb{k}_{\perp}/k_{\parallel}}{\gamma(1-\mb{\beta} k_0/k_{\parallel})}
=\frac{\tan\theta}{\gamma(1-\beta/\cos\theta)}\notag\\
&=\frac{\sin\theta}{\gamma(\cos\theta-\beta)}
\tag{9}
\end{align}
系 \(K’\) での波の方向 \(\theta’\) を用いて, 角振動数 \(\omega’\) を表わすと便利なことがある．式 (8) の逆変換は, ダッシュを入れ替え \(\beta\to-\beta\) とすれば良い：
\begin{equation}
\omega=\gamma\omega'(1+\beta\cos\theta’)
\tag{10}
\end{equation}
\omega=\gamma\omega'(1+\beta\cos\theta’)
\tag{10}
\end{equation}
これを使うと, 求める式は次となる：
\begin{equation}
\omega’=\frac{\omega}{\gamma\left(1+\beta\cos\theta’\right)}
=\frac{\omega\sqrt{1-\beta^{2}}}{1+\beta\cos\theta’}
\tag{11}
\end{equation}
\omega’=\frac{\omega}{\gamma\left(1+\beta\cos\theta’\right)}
=\frac{\omega\sqrt{1-\beta^{2}}}{1+\beta\cos\theta’}
\tag{11}
\end{equation}
導出過程から, この式は「角振動数\(\omega\)の光源に対して,観測者が速度\(\mb{v}\)で遠ざかる場合」を考えたときの結果である．それに対して, 例えば J.B.ハートル 「重力」 §5.5 では「光源が観測者に近づいて来る場合」を議論している．その場合は \(\beta\to-\beta\), または角度 \(\theta’\) が \(\pi-\theta’\) となる．その結果, 分母の符号がマイナスになるので注意が必要である：
\begin{equation}
\cos(\pi-\theta’)=-\cos\theta’,\quad\rightarrow\quad
\omega’=\frac{\omega\sqrt{1-\beta^{2}}}{1-\beta\cos\theta’}
\tag{11′}
\end{equation}
\cos(\pi-\theta’)=-\cos\theta’,\quad\rightarrow\quad
\omega’=\frac{\omega\sqrt{1-\beta^{2}}}{1-\beta\cos\theta’}
\tag{11′}
\end{equation}
式(8)は, 普通の Doppler 効果の公式に分母の平方根の因子による修正が加わったものである．速度 \(\mb{v}\) が小さい場合では \(\gamma\approx 1\) として, 式 (11)’ は \(\omega’\approx \omega(1+\beta\cos\theta’)\) と近似される． \(\theta’=0\) のとき, 光子は光源の運動方向と同じ方向に放出されており, \(\cos\theta’=1\) であるから, 光子の振動数は青方偏移 \(\Delta\omega=+\beta\omega\) を受ける． また, \(\theta’=\pi\) のとき, 光子は光源の運動方向と反対方向に運動しており, \(\cos\theta’=-1\) であるから, 赤方偏移 \(\Delta\omega=-\beta\omega\) を受けることになる． ( 下図 2. を参照のこと)．
平方根の因子の存在は, \(\theta’=\pi/2\) の場合にも「横方向のDoppler効果」が存在することを表している．この場合 \(\cos\theta’=0\) であるから, 式 (11′) は,
\begin{equation}
\omega’=\omega\sqrt{1-\beta^{2}},\quad\rightarrow\quad
\omega’\approx \omega\left(1-\frac{1}{2}\beta^{2}\right)\quad\Rightarrow\quad
\Delta\omega’=-\frac{1}{2}\beta^{2}\omega
\tag{12}
\end{equation}
\omega’=\omega\sqrt{1-\beta^{2}},\quad\rightarrow\quad
\omega’\approx \omega\left(1-\frac{1}{2}\beta^{2}\right)\quad\Rightarrow\quad
\Delta\omega’=-\frac{1}{2}\beta^{2}\omega
\tag{12}
\end{equation}
物体の固有時を \(\tau_0\), 観測者の時間を \(\tau\) とすると,
\begin{equation}
\tau_0=\frac{\tau}{\sqrt{1-\beta^{2}}},\quad \omega’\tau_0 = \omega\tau,\quad \rightarrow\
\omega’=\omega\frac{\tau}{\tau_0}=\omega\sqrt{1-\beta^{2}}
\tag{13}
\end{equation}
\tau_0=\frac{\tau}{\sqrt{1-\beta^{2}}},\quad \omega’\tau_0 = \omega\tau,\quad \rightarrow\
\omega’=\omega\frac{\tau}{\tau_0}=\omega\sqrt{1-\beta^{2}}
\tag{13}
\end{equation}
従って, 式 (12) は単に「時間の遅れの式」に等価であることが分かる．式 (12) から, この「横ドップラー効果」は \(\beta^{2}\) のオーダーの「赤方偏移」である．この「相対論的な横方向のDoppler効果」は, 運動中の原子の分光測定によって観測されている．また, 高速で回転している円筒の軸上にガンマ線源を置き, 円筒面上に吸収体を取り付けた装置を用いて, 精密な共鳴吸収の技術によってこの効果を観測することが出来る．
相対論的ビーミング
相対論的ビーミングの現象は, 光子の空間的運動量の公式から得ることが出来る．「系 \(K\) に対して, 系\(K’\) 上の光源は速度 \(\mb{v}=c\mb{\beta}\) で動いている」とする．そのときの「光源速度 \(\mb{v}\) に対して角度 \(\theta\) をなす方向に放射される光線 (光子)」について考えて見る．この場合の ４-波数ベクトルのローレンツ変換は, 光源が動いているので式 (5) に於いて \(\beta\to-\beta\) としたものとなる：
\begin{equation}
k’_{0}=\gamma(k_{0}+\mb{\beta}\cdot\mb{k})=\gamma(k_{0}+\beta k_{\parallel}),\quad
k’_{\parallel}=\gamma(k_{\parallel}+\mb{\beta}k_{0}),\quad
\mb{k}’_{\perp}=\mb{k}_{\perp}
\tag{14}
\end{equation}
k’_{0}=\gamma(k_{0}+\mb{\beta}\cdot\mb{k})=\gamma(k_{0}+\beta k_{\parallel}),\quad
k’_{\parallel}=\gamma(k_{\parallel}+\mb{\beta}k_{0}),\quad
\mb{k}’_{\perp}=\mb{k}_{\perp}
\tag{14}
\end{equation}
また, 通常の ３ 次元波数ベクトルの大きさを \(k=|\mb{k}|\) とすると, 波数ベクトルの空間的関係について次のことが言える：
\begin{equation}
\mb{k}=\mb{k}_{\perp}+\mb{k}_{\parallel},\quad k=\frac{\omega}{c}=k^{0},\quad
\cos\theta=\frac{\mb{k}_{\parallel}}{k}=\frac{\mb{k}_{\parallel}}{k^{0}},\quad
\cos\theta’=\frac{\mb{k}’_{\parallel}}{k’^{0}}
\tag{15}
\end{equation}
\mb{k}=\mb{k}_{\perp}+\mb{k}_{\parallel},\quad k=\frac{\omega}{c}=k^{0},\quad
\cos\theta=\frac{\mb{k}_{\parallel}}{k}=\frac{\mb{k}_{\parallel}}{k^{0}},\quad
\cos\theta’=\frac{\mb{k}’_{\parallel}}{k’^{0}}
\tag{15}
\end{equation}
そこで, 式 (14) を用いて \(\cos\theta\) を表わすと,
\begin{equation}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\cos\theta’ =\frac{k’_{\parallel}}{k’_{0}}=\frac{\gamma(k_{\parallel}+\mb{\beta}k_{0})}{\gamma(k_{0}+\beta k_{\parallel})}
=\frac{\ds{\frac{k_{\parallel}}{k_{0}}+\beta}}{\ds{1+\beta\frac{k_{\parallel}}{k_{0}}}}
=\frac{\cos\theta+\beta}{1+\beta\cos\theta}
\tag{16}
\end{equation}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\cos\theta’ =\frac{k’_{\parallel}}{k’_{0}}=\frac{\gamma(k_{\parallel}+\mb{\beta}k_{0})}{\gamma(k_{0}+\beta k_{\parallel})}
=\frac{\ds{\frac{k_{\parallel}}{k_{0}}+\beta}}{\ds{1+\beta\frac{k_{\parallel}}{k_{0}}}}
=\frac{\cos\theta+\beta}{1+\beta\cos\theta}
\tag{16}
\end{equation}
よって, 次の関係が得られる：
\begin{equation}
\cos\theta’=\frac{\beta+\cos\theta}{1+\beta\cos\theta}
\tag{17}
\end{equation}
\cos\theta’=\frac{\beta+\cos\theta}{1+\beta\cos\theta}
\tag{17}
\end{equation}
または \(c=1\) の単位系で表わすならば \(\beta=v/c=v\) であるから,
\begin{equation}
\cos\theta’=\frac{v+\cos\theta}{1+v\cos\theta}
\tag{17′}
\end{equation}
\cos\theta’=\frac{v+\cos\theta}{1+v\cos\theta}
\tag{17′}
\end{equation}
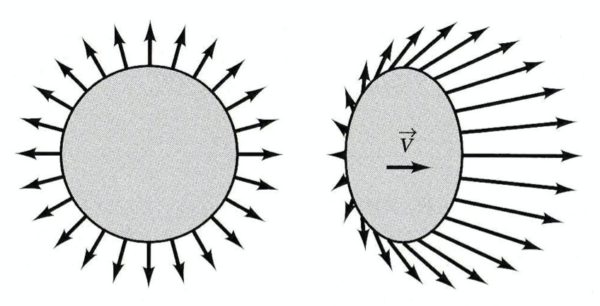
この式から, 光源系で前面の半球内 (\(|\theta|<\pi/2\)) に放出された光子は, 小さい円錐 \(|\theta’|<\alpha\) に放出されたと観測者には見える．ただし \(\alpha\) は \(\theta=\pi/2\) のときの角度 \(\theta’\) である． \(v\) が \(1\) に近いと, 開いた角度 \(\alpha\) は小さくなるであろう．つまり, 光子は光源の運動方向に絞られる (図 1. 及び 図 2. を参照のこと)．
ドップラー偏移から前面に放出された光子のエネルギーは, 後方の光子よりも大きいことが分かる． これは, 放射の強度が運動方向に強く集中することを意味する．一様に放射を放ちながら向かって来る物体は,離れて行く方向から見るよりも明るくなる．これが「相対論的ビーミング」である．
また, 特殊相対性理論の可視化の観点から式 (17) を解釈するならば, 「光の収差」( Aberration of light ) が生じることが分かる．式 (17) から,「観測者は「前方の物体は周辺より小さい立体角(視野角)中にある」と認識するので, 前方の物体はずっと遠くの方にあるように見える事になる．更にまた, 静止した観測者に背後から斜めに到着する光線は, 動いている観測者には前方から斜めにやって来る事になる．このため, ハイスピードカメラであれば背後に位置する物体を写すことが出来るであろう」．
図 1. 式 (15) で \(v=0.9\) の場合に, \(\theta\) を \(\pi/15\) ごとに増やしたときの, \(\theta’\) の増加する様子を光線 (矢印) で表したもの．ただし, 運動方向すなわち \(v\) の向きは右横向きである．
図 2. 相対論的ビーミング．左図は静止系で全ての方向に同じように光を放っている物体である．表面から垂直に 24 本の光子の波数ベクトルが出ている．右図に, 速さ \(V=0.75\) で右に運動する系に静止している物体が同じ 24 個の光子とともにローレンツ収縮しているところを示した． \(V\) が光速に近づくと光子は運動方向に向いて行き, 波数ベクトルの運動方向の成分は, ドップラー効果のために大きくなって行くので, 放射強度は益々運動方向に集中されて行く．また, 物体が球体であると, その物体は運動方向にローレンツ収縮をするので回転楕円体の様になる．
