
\(\)
§ 7.7 THE HAMILTONIAN は,「時間のズレに対する遷移要素の1次変化からシュレディンガー方程式およびハミルトニアン \(H\) の表現が得られる」ことを述べている.しかし, 最後の結果であるシュレディンガー方程式の符号が違っている!.結果式が違うのだから, その導出過程の何処かが間違っているはずである.そこで, この節の文章全体を, 正しい符号となるように修正して (式への補足や図も加えて) 示しておくことにする.
7-7 ハミルトニアン(THE HAMILTONIAN)
これまで導いてきた事柄を用いると, ハミルトニアンに対する遷移振幅を書き下すことは非常に容易であるように思われる.運動量の2乗に対する遷移振幅を求め, それを \(2m\) で割り算する.そしてポテンシャルに対する遷移振幅を加えるのである.このやり方をするならば, 時刻 \(t_k\) に於けるハミルトニアン自体は次のように書くことが出来るだろう:
\def\BraKet#1#2#3{\langle #1 | #2 | #3 \rangle}
\def\BK#1#2{\langle #1 | #2 \rangle}
\def\reverse#1{\frac{1}{#1}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
H_k=\frac{m}{2}\left(\frac{x_{k+1}-x_k}{\varepsilon}\right)\left(\frac{x_k-x_{k-1}}{\varepsilon}\right)
+V(x_k)
\tag{7-112}
\end{equation}
一方, 演算子の形式ではハミルトニアンの遷移要素は次である:
\BraKet{\chi}{H}{\psi}=\int_{-\infty}^{\infty}\chi^{*}\,\left[\frac{p^{2}}{2m}+V(x)\right]\,\psi\,dx
=\int_{-\infty}^{\infty} \chi^{*}\,H\,\psi\,dx
\tag{7-113}
\end{equation}
ハミルトニアンに対する遷移振幅を定義するこの方法は, 完全に正しい結果を与えるけれども, 多少不自然なものである.なぜなら, これはハミルトニアンと時間の間の重要な関係を表現していないからである.従って, 次にこの遷移要素に対する別の定義を考える.それは, 時間をズラせたときに起こる状態変化を調べることに基づいた定義方法である.この方法では, \(S\) の形が与えられさえすれば, それがどんなに複雑であっても \(H_k\) を定義することが可能である.
このことを調べるために, ちょうど経路積分を定義したときのように時間軸を無限小の区間に分割する.しかしここでは, 時間を同じ長さの区間に分割することは必要でないことに注意しておこう.明らかに, 同じ区間に分割することは全く必要ないのである.時間をどんな時刻 \(t_i\) に分割しようとも満足できるものである.極限操作は, 最大の時間間隔 \(t_{i+1}-t_i\) をゼロに収束させることによって表現される.
単純化のために, 考える系は 1 粒子の 1 次元運動から構成されているとしよう.その作用は次の和で表現される:
S=\sum_i S[x_{i+1},t_{i+1}; x_i,t_i]
\tag{7-114}
\end{equation}
ただし,
S[x_{i+1},t_{i+1}; x_i,t_i]=\int _{t_i}^{t_{i+1}} L[\dot{x}(t),x(t),t]\,dt
\tag{7-115}
\end{equation}
この式中の積分は \((x_i,t_i)\) と \((x_{i+1},t_{i+1})\) の間の古典的経路について行う.ここでの1次元の例では, 十分よい近似で次のように書くことが出来る:
S[x_{i+1},t_{i+1}; x_i,t_i]\simeq L(i)\,\varepsilon
=\left[\frac{m}{2}\left(\frac{x_{i+1}-x_i}{t_{i+1}-t_i}\right)^{2}-V(x_{i+1})\right](t_{i+1}-t_i)
\tag{7-116}
\end{equation}
時刻 \(t_i\) の \(x_i\) についての積分に伴う規格化定数は, 前に用いたものと同じである.すなわち,
A=\sqrt{\frac{2\pi\hbar\,i\,(t_{i+1}-t_i)}{m}}
\tag{7-117}
\end{equation}
時間のズレに対する状態の変化と \(H\) との関係をこれから調べる.時空(space-time)のある領域 \(R\) に於いて定義される状態 \(\psi(t)\) を考える.同じ時刻 \(t\) に別の領域 \(R_\delta\) で定義される状態 \(\psi_{\delta}(t)\) を想像しよう.そして領域 \(R_\delta\) は領域 \(R\) と全く同じであるが, 時間が \(\delta\) だけ早い, すなわち「丸ごと過去の方へ時間 \(\delta\) だけ移されていることだけが異なる」と仮定するのである. \(R_{\delta}\) において系を準備するのに要する装置は全て \(R\) に於いて系を準備する装置と同じであって, 違いは前者が「時間が \(\delta\) だけ早く操作されたこと」である.もしラグランジアン \(L\) が時間に陽に依存する場合には \(L\) もずらす必要がある.すなわち, 状態 \(\psi_{\delta}\) は状態 \(\psi\) に対する \(L\) から得られるのだが, \(L_{\delta}\) を書く場合には「時間変数だけは \(t+\delta\) とする」のである.
状態 \(\psi_{\delta}\) は \(\psi\) とどのように違って来るだろうか?. どのような測定をする場合でも, 系がある固定した領域 \(R’\) に見出される確率は, 元の領域が \(R\) であったか \(R_{\delta}\) であったかによって違ってくる.時刻 \(t_k\) に於いて, それ以前の時間を \(\delta\) だけシフトするとき, 遷移要素 \(\langle\chi|1|\psi\rangle\) はどれくらい変化するかを考えてみよう.この時間シフトの影響は,「\(i\leq k\) の場合には \(t_i\) の全ての値を \(\delta\) だけ減少させ, \(i\gt k\) の場合には全ての \(t_i\) をそのままにして置く」と見做せばよい.
この時点で読者が先の事を考えたならば, 困難が待ち受けているように見えるであろう.明らかに, 我々の意図するのは, 全ての無限小時間間隔が減少して結局はゼロとなるような極限をとることである.しかしながら, このままのやり方では, 少なくとも 1 つの時間間隔 \(\Delta t_k=t_{k+1}-t_k\) が下限を持つので, 無限に小さくすることが出来ない (時刻 \(t_{k+1}\) はそのままだが \(t_k\) 以前は一様に \(-\delta\) だけズレるので, \(\varepsilon\to 0\) としても \(\Delta t_k=\varepsilon+\delta\to\delta\) となり \(\delta\) より小さくはならないから!?). この困難は, 時間のズレ \(\delta\) 自身が時間の関数であると仮定することで解決することが出来る. 時間のズレ \(\delta\) として「\(t=t_k\) より前から滑らかに始まり \(t=t_k\) の後で滑らかに止まるようなもの」を思い描くことが出来る.このとき時間変分 \(\delta\) を固定して, \(\Delta t_k=t_{k+1}-t_k\) も含め全ての時間間隔を滑らかにゼロにする.そして \(\delta\) をゼロに収束させることにより, この時間のズレの1次の効果を調べるのである.このより厳密な手続きによって得られる結果は, 本質的には本節の例で用いている手続きによる結果と同じものになる.
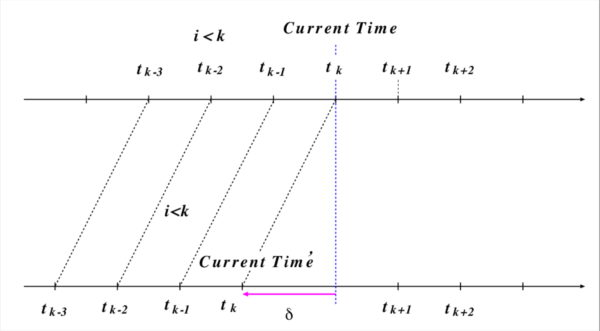
図 1 考えている時刻 \(t_k\) 以前の時間を \(\delta\) だけ過去に動かす.すると \(i\le k\) 以前の時間間隔は一様に \(\delta\) だけシフトして減少するだけでその間隔は変化しない.
時間のズレの効果を調べることに立ち戻ってみると, 式 (7-115) で定義された作用は \(i\le k\) の場合の作用 \(S[x_{i+1},t_{i+1};x_i,t_i]\) は \(t_{i+1}\) と \(t_i\) が共に同じだけ変化する限り変化することはない.しかし \(i=k\) の作用 \(S[x_{k+1},t_{k+1};x_k,t_k]\) だけは \(S[x_{k+1},t_{k+1};x_k,t_k-\delta]\) に変わる.更に \(x_k\)
についての積分に伴う定数 \(A\) も変化し次となる:
A_k=\sqrt{\frac{2\pi\hbar\,i\,(t_{k+1}-t_k+\delta)}{m}}
\tag{7-118}
\end{equation}
式 (7-2) を用いて遷移要素を定義する.経路積分が作用 \(S\) と規格化定数 \(A\) の両方に依存する(両方とも時間移動によって変化する)ことを考慮すると, 遷移要素の \(\delta\) について1次の変化を次のように表わすことが出来る:
\BraKet{\chi}{1}{\psi_\delta}-\BraKet{\chi}{1}{\psi}=-\frac{i\delta}{\hbar}\left\langle\,\chi\,\left|\,
\ppdiff{S[x_{k+1},t_{k+1};x_k,t_k]}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\,\right|\,\psi\,\right\rangle
\tag{7-119}
\end{equation}
ただし, 第2項は \(A\) の変化から由来している.
【 補足 1 】 **********************************************************************************************
遷移要素の変化量はその経路積分部分の変化量に依ると考える.その経路積分の変化は, 本文中にあるように \(\Delta t_k=t_{k+1}-t_k\) の部分の作用 \(S_k\) に於いて生じるだけである.そこではその規格化定数 \(A_k\) も変化するのであった.\(S_k\) の変化を考える時には \(L_\delta\) に於いて \(t_k\) が \(dt_k=\delta\) だけ変化するとすべきであるから, 核 \(K_k=(1/A_k)e^{iS_k/\hbar}\) の変化量は次のように書ける:
\begin{align*}
dK_k&=\ppdiff{K_k}{A_k}\ppdiff{A_k}{t_k}dt_k + \ppdiff{K_k}{S_k}\ppdiff{S_k}{t_k}dt_k
=-\reverse{A_k^{2}}e^{iS_k/\hbar}\ppdiff{A_k}{t_k}dt_k + \reverse{A_k}\frac{i}{\hbar}e^{iS_k/\hbar}
\ppdiff{S_k}{t_k}dt_k
\end{align*}
このとき, \(A_k=\left[2\pi\hbar\,i\,(t_{k+1}-t_k)/m\right]^{1/2}\) だから,
\begin{align*}
-\reverse{A_k^{2}}\ppdiff{A_k}{t_k}&=-\left[\frac{2\pi\hbar\,i\,(t_{k+1}-t_k)}{m}\right]^{-1}
\times\reverse{2}\left[\frac{2\pi\hbar\,i\,(t_{k+1}-t_k)}{m}\right]^{-1/2}
\times\left(\frac{-2\pi\,i\hbar}{m}\right)\\
&=\frac{m}{2\pi\hbar i(t_{k+1}-t_k)}\times\frac{2\pi i\hbar}{m}\times \frac{1}{2}\reverse{A_k}
=\reverse{2(t_{k+1}-t_k)}\reverse{A_k}
\end{align*}
よって \(dt_k=-\delta\) として,
\begin{align*}
dK_k&=dt_k\left(-\reverse{A_k^{2}}\ppdiff{A_k}{t_k}e^{iS_k/\hbar} + \frac{i}{\hbar}\reverse{A_k}e^{iS_k/\hbar}\ppdiff{S_k}{t_k}\right)\\
&=-\delta\left(\reverse{2(t_{k+1}-t_k)}\reverse{A_k} + \frac{i}{\hbar}\reverse{A_k}\ppdiff{S_k}{t_k}\right)e^{iS_k/\hbar}\\
&=-\delta\reverse{A_k}e^{iS_k/\hbar}\left[\frac{i}{\hbar}\ppdiff{S_k}{t_k}+\reverse{2(t_{k+1}-t_k)}\right]
=-\frac{i\delta}{\hbar}K_k\left[\ppdiff{S_k}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\right]
\end{align*}
すると振幅 \(K(b,a)\) の変化量は式(2-33)に於いて \(K_k\) だけが上式だけ変化したものだから,
\begin{align*}
dK(b,a)&=\idotsint dx_1dx_2\dotsb dx_{N-1}\,K(b,N-1)K(N-1,N-2)\dotsb dK(k+1,k)\dotsb K(1,a)\\
&=-\frac{i\delta}{\hbar}\idotsint dx_1dx_2\dotsb dx_{N-1}\,K(b,N-1)\dotsb K(k+1,k)\left[\ppdiff{S_k}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\right]\dotsb K(1,a)\\
&=-\frac{i\delta}{\hbar}\idotsint dx_1dx_2\dotsb dx_{N-1}\,K(b,N-1)\dotsb K(k+1,k)\dotsb K(1,a)\left[\ppdiff{S_k}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\right]
\end{align*}
従って,再び式 (2-33)を用いれば,
dK(b,a)=-\frac{i\delta}{\hbar}K(b,a)\left[\ppdiff{S_k}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\right]
=-\frac{i\delta}{\hbar}\int_a^{b}\mathscr{D}x(t)\,e^{iS[b,a]/\hbar}\left[\ppdiff{S_k}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\right]
\end{equation*}
よって最終的に, 遷移要素の \(\delta\) の1次の変化量は次となる:
\begin{align*}
d\BraKet{\chi}{1}{\psi}&=\BraKet{\chi}{1}{\psi_\delta}-\BraKet{\chi}{1}{\psi}
=\int dx_b\int dx_a\,\chi^{*}(x_b)\,dK(b,a)\,\psi(x_a)\\
&=-\frac{i\delta}{\hbar}\int dx_b\int dx_a\,\chi^{*}(x_b)\int \mathscr{D}x(t)\,\left[\ppdiff{S_k}{t_k}
+\frac{\hbar}{2i(t_{k+1}-t_k)}\right]\,e^{iS[b,a]/\hbar}\,\psi(x_a)\\
&=-\frac{i\delta}{\hbar}\left\langle\,\chi\,\left|\,\ppdiff{S_k}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\,
\right|\,\psi\,\right\rangle
\end{align*}
*********************************************************************************************************
我々は, 量子力学のハミルトニアンに対応する汎関数を次のように定義したい:
H_k=\ppdiff{S[x_{k+1},t_{k+1};x_k,t_k]}{t_k}+\frac{\hbar}{2i\,(t_{k+1}-t_k)}
\tag{7-120}
\end{equation}
右辺の第1項は古典的ハミルトニアンの定義である.第2項は量子力学的定義に於いて必要な項であり, 時間間隔 \(t_{k+1}-t_k\) がゼロになるとき, \(H_k\) が有限となるようにするためのものである.この最後の項は, 時間移動 \(\delta\) による規格化因子 \(A\) の変化からの帰結(consequence)である.
この結果を, 式 (7-116) に示されている具体的な1次元の例に適用して見よう.すると演算子 \(H_k\) は, 次のように書くことが出来る:
H_k&=\frac{m}{2}\left(\frac{x_{k+1}-x_k}{t_{k+1}-t_k}\right)^{2}+\frac{\hbar}{2i(t_{k+1}-t_k)}+V(x_{k+1})\notag\\
&=\frac{m}{2}\left(\frac{x_{k+1}-x_k}{t_{k+1}-t_k}\right)\left(\frac{x_k-x_{k-1}}{t_k-t_{k-1}}\right)+V(x_k)
\tag{7-121}
\end{align}
2番目の式は, 式 (7-54) で \(\varepsilon=t_{k+1}-t_k\) とした結果に基づいている.このように, 速度の積を2つの相続く速度の積で表わすと, 一見異質な項 \(\displaystyle{\frac{\hbar}{2i(t_{k+1}-t_k)}}\) を避けることが出来るのである!.
【 補足 2 】 **********************************************************************************************
( i ) 式 (7-120)の右辺にある \(t_k\) による偏微分は, 微小時間 \(\varepsilon=t_{k+1}-t_k\) で割り算するという意味になる.従って, 式 (7-116) の両辺を \((t_{i+1}-t_i)\) で割り算すると, 次式を得る:
\ppdiff{S}{t_k}\ \Rightarrow\ \frac{S[x_{k+1},t_{k+1};x_k,t_k]}{(t_{k+1}-t_k)}=\frac{m}{2}
\left(\frac{x_{k+1}-x_k}{t_{k+1}-t_k}\right)^{2}-V(x_{k+1})
\end{equation*}
( ii ) 式 (7-121) は, 次が言えるからである. 式 (7-54) に於いて \(\varepsilon=t_{k+1}-t_k\) とすると,
\begin{align*}
&\left\langle \frac{m}{2}\left(\frac{x_{k+1}-x_k}{\varepsilon}\right)\left(\frac{x_k-x_{k-1}}{\varepsilon}
\right)\right\rangle=\left\langle \frac{m}{2}\left(\frac{x_{k+1}-x_k}{\varepsilon}\right)^{2}\right\rangle
+\frac{\hbar}{2i\varepsilon}\langle 1 \rangle\\
&\Rightarrow\quad
\left\langle \frac{m}{2}\left(\frac{x_{k+1}-x_k}{t_{k+1}-t_k}\right)\left(\frac{x_k-x_{k-1}}{t_k-t_{k-1}}
\right)\right\rangle-\frac{\hbar}{2i(t_{k+1}-t_k)}\langle 1 \rangle
=\left\langle \frac{m}{2}\left(\frac{x_{k+1}-x_k}{t_{k+1}-t_k}\right)^{2}\right\rangle
\end{align*}
*********************************************************************************************************
次に状態関数 \(\psi(t)\) の1次変化を考える.\(\psi(t_\delta)\) は \(\psi(t)\) を \(-\delta\) だけ平行移動したものであるから, それを \(\psi(t_\delta)\) と表すならば次式が得られる:
\[
\psi(t_\delta)= \psi(t+\delta)=\psi(t)+\delta\ppdiff{\psi}{t}
\tag{7-122}
\]
この式は, 2つの領域 \(R,\,R_\delta\) で定義される状態関数 \(\psi\) を結び付けるものである.従って, 式 (7-119), 式 (7-120) そして式 (7-121) を組み合わせることにより, 演算子をシュレディンガー方程式にそして経路積分へと結び付ける関係サイクルは閉じられるのである:
\delta\,\biggl\langle\,\chi\,\biggl|\,1\,\biggr|\ppdiff{\psi}{t}\,\biggr\rangle=-\frac{i}{\hbar}\delta\,
\BraKet{\chi}{H}{\psi}
\tag{7-123}
\end{align}
これは, 再び Schrödinger 方程式に戻ることになる:
\[-\frac{\hbar}{i}\ppdiff{\psi}{t}=H\psi
\tag{7-124}
\]
作用がどんな複雑な場合でも, そのハミルトニアン(すなわちエネルギーに相当する汎関数) の表現は「時刻 \(t\) より前の全ての時刻を \(-\delta\) だけ移動させたときの遷移要素 \(\BraKet{\chi}{1}{\psi}\) の1次の変化を求め, その変化を \(\displaystyle{-\delta\frac{i}{\hbar}\BraKet{\chi}{H(t)}{\psi}}\) と書くこと」により見出すことが可能である.
【 補足 3 】 **********************************************************************************************
( i ) 式 (7-122) は, 関数 \(f(t)\) を \(t\) 軸の方向に \(-a\) だけ平行移動した関数が \(f(t+a)\) となることを用いればよいのである. 前回のブログ記事で扱ったファインマンの論文:「Space-Time Approach to Non-Relativistic Quantum Mechanics」にも, 次のように書かれている:
The wave function \(\psi_{\delta}(x, t)\) represents, of course, the same state as \(\psi(x, t)\) will be after time \(\delta\), i.e., \(\psi(x, t + \delta)\).
しかしながら, この式 (7-122) の部分の文章は原書と校訂版で次のような記述になっている:
Using the relation \(t_{\delta}=t-\delta\) for all values of \( t < t_k \), we have
\begin{equation*}
\psi(t)=\psi(t_\delta)+\delta\ppdiff{\psi}{t}=\psi_\delta+\delta\ppdiff{\psi}{t}
\tag{7-122}
\end{equation*}
connecting the function \(\psi\) defined in the two regions \(R\) and \(R_{\delta}\).
しかし, それでは下の (ii) のような議論が成り立たず, 式 (7-123) は得られないようである.なので, 自己流に修正してしまってあるので注意する!.
( ii ) 式 (7-122) より \(\displaystyle{\delta\ppdiff{\psi}{t}=\psi(t_\delta)-\psi(t)}\) であり \(\delta\) は微小な定数であった.従って, この遷移要素は次となる:
\left\langle\,\delta\,\ppdiff{\psi}{t}\,\right\rangle=\delta\left\langle\,\ppdiff{\psi}{t}\,\right\rangle
=\left\langle\,\psi(t_\delta)\,\right\rangle-\left\langle\,\psi(t)\,\right\rangle,
\quad\rightarrow\quad \delta\,\left\langle\,\chi\,\biggl|\,1\,\biggr|\,\ppdiff{\psi}{t}\,\right\rangle
=\BraKet{\chi}{1}{\psi_\delta}-\BraKet{\chi}{1}{\psi}
\end{equation*}
これに式 (7-119) 及び式 (7-120) を代入すると,
\begin{align*}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\delta\,\left\langle\,\chi\,\biggl|\,1\,\biggr|\,\ppdiff{\psi}{t}\,\right\rangle
&=\BraKet{\chi}{1}{\psi_\delta}-\BraKet{\chi}{1}{\psi}
=-\frac{i\delta}{\hbar}\left\langle\,\chi\,\left|\,\ppdiff{S_k}{t_k}+\frac{\hbar}{2i(t_{k+1}-t_k)}\,\right|\,\psi\,\right\rangle\\
&=-\delta\,\frac{i}{\hbar}\BraKet{\chi}{H_k}{\psi}\\
\Rightarrow\quad \left\langle\,\chi\,\biggl|\,1\,\biggr|\,\ppdiff{\psi}{t}\,\right\rangle
&=\left\langle\,\chi\,\biggl|\,\pdiff{t}\,\biggr|\,\psi\,\right\rangle
=-\frac{i}{\hbar}\BraKet{\chi}{H_k}{\psi}
=\left\langle\,\chi\,\biggl| \reverse{i\hbar}H_k \biggr|\psi\,\right\rangle
=\left\langle\,\chi\,\biggl| 1 \biggr|\reverse{i\hbar}H_k\psi\,\right\rangle
\end{align*}
従って, 式 (7-124) に相当した式を得る:
\ppdiff{\psi}{t}=\reverse{i\hbar}H_k\psi,\quad\text{or}\quad i\hbar\ppdiff{\psi}{t}=H\,\psi
\end{equation*}
*********************************************************************************************************

