\(\)
Problem 6-16
Interpret Eq.(6.71) as a sum over alternatives; i.e., identify the alternatives.
(解答例) 時刻 \(t_3\) に於ける状態 \(n\) と状態 \(m\) 間のポテンシャル \(V\) の行列要素の式(6-71)は, 全時空 \(\tau=(x,t)\) のうちの主にポテンシャル場 \(V(x,t)\) が存在する領域に於いて, 量 \(\phi_m^{*}(x_3)V(x_3,t_3)\phi_n(x_3)\) の全てを位置 \(x_3\) で積分したものである：
\begin{equation}
V_{mn}(t_3)=\int_{-\infty}^{\infty}dx_3\,\phi^{*}_m(x_3)\,V(x_3,t_3)\,\phi_n(x_3)
\tag{6-71}
\end{equation}
V_{mn}(t_3)=\int_{-\infty}^{\infty}dx_3\,\phi^{*}_m(x_3)\,V(x_3,t_3)\,\phi_n(x_3)
\tag{6-71}
\end{equation}
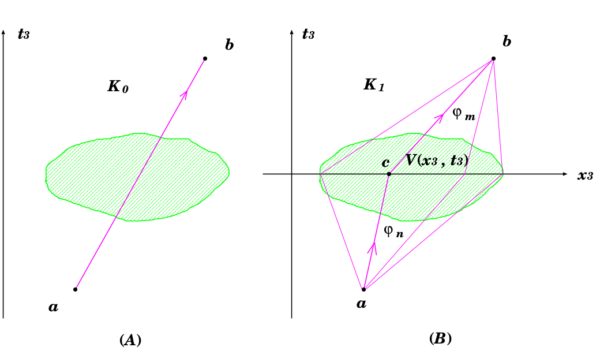
これは「粒子が時刻 \(t_3\) においてポテンシャル場 \(V(x,t)\) が存在する領域中の位置 \(x_3\) で散乱されるときの量 \(\phi_m^{*}(x_3)V(x_3,t_3)\phi_n(x_3)\) を全て足し合わせること」と解釈される．従って, 各々の選択肢(alternative) は, 下図の図 (B) に示されている経路たちのように,「ポテンシャル領域に於いて散乱される位置 \(x_3\) が異なった運動に対応する」ことを意味する．
図 (A) : 粒子が散乱を受けないゼロ次の核 \(K_0\)．この場合, \(\lambda_{mn}=\delta_{mn}e^{-iE_n(t_2-t_1)/\hbar}\) である．
図 (B) : 一回散乱される1次の核 \(K_1\)． この場合, \(\lambda_{mn}\) 中の行列要素 \(V_{mn}(t_3)\) は, 図のように時刻 \(t_3\) におけるポテンシャル領域の全ての位置 \(x_3\) での散乱経路を足し合わせたもの即ち積分したものとなる．
