問題 6-17 の解答例

Problem 6-17
Interpret Eq. (6-72) by explaining the meaning of each term. Then explain and verify the equation for the second-order coefficient

\begin{matrix} (6-74) & λ_{m n}^{(2)} = {(- \frac{i}{ℏ})}^{2} \int_{t_{1}}^{t_{2}} d t_{4} \int_{t_{1}}^{t_{4}} d t_{3} \sum_{k} e^{- i E_{m} (t_{2} - t_{4}) / ℏ} V_{m k} (t_{4}) e^{- i E_{k} (t_{4} - t_{3}) / ℏ} V_{k n} (t_{3}) e^{- i E_{n} (t_{3} - t_{1}) / ℏ} \end{matrix}

(解答例)　式 (6-72) は次であった：

\begin{matrix} (6-72) & λ_{m n}^{(1)} = - \frac{i}{ℏ} e^{- i (E_{m} t_{2} - i E_{n} t_{1}) / ℏ} \int_{t_{1}}^{t_{2}} d t_{3} V_{m n} (t_{3}) e^{i (E_{m} - E_{n}) t_{3} / ℏ} \end{matrix}

この式は, 式 (6-70) の「遷移振幅」( transition amplitude ) の1次の項

λ_{m n}^{(1)}

に同値である：

\begin{matrix} (6.70) & λ_{m n}^{(1)} = - \frac{i}{ℏ} \int_{t_{1}}^{t_{2}} d t_{3} \int_{- \infty}^{\infty} d x_{3} ϕ_{m}^{*} (x_{3}) V (x_{3}, t_{3}) ϕ_{n} (x_{3}) e^{(i / ℏ) [E_{m} (t_{3} - t_{2}) - E_{n} (t_{3} - t_{1})]} \end{matrix}

これは「時刻

t_{1}

から運動をして来た状態

ϕ_{n}

の自由粒子が, 時刻

t_{2}

でポテンシャル領域中の位置

x_{3}

で 1 回の散乱を受けて状態

ϕ_{m} (x_{3})

に遷移し, その後自由粒子として運動して, 時刻

t_{2}

に状態

ϕ_{m}

で見出される確率振幅」を表している．
　次に, 式 (6-17) の第 3 項目は以下であった：

\begin{matrix} (1) & K_{V}^{(2)} (2, 1) = {(- \frac{i}{ℏ})}^{2} \int d τ_{4} \int d τ_{3} K_{0} (2, 4) V (4) K_{0} (4, 3) V (3) K_{0} (3, 1) \end{matrix}

このことから「遷移振幅の 2 次の係数」

λ_{m n}^{(2)}

の意味と, 上式 (1) が式 (6-74) の形になることを確かめて行こう．式 (1) は, 下図 1 のような 2 回の散乱過程の場合の遷移核

K^{(2)}

に相当するのであった．

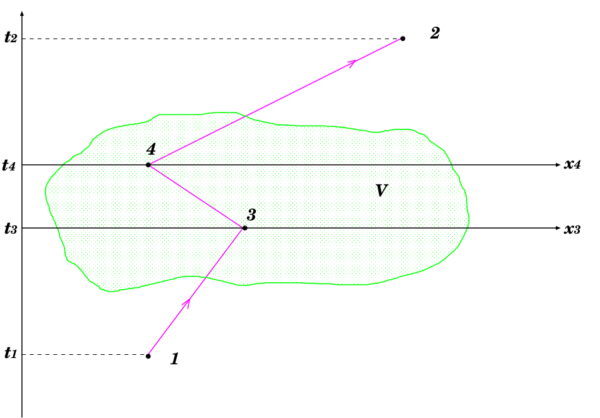
図 1. 時刻 $t_{3}$ と $t_{4}$ で散乱されるとすると, 2次(2回散乱)の核 $K_{2}$ に相当する 2 次の係数 $λ_{m n}^{(2)}$ は, ポテンシャル領域の全ての位置 $x_{4}$ と $x_{3}$ で散乱経路を足し合わせたもの, すなわち積分したもの $V_{m k} (t_{4})$ と $V_{k n} (t_{3})$ を, 更に時間 $t_{4}$ と $t_{3}$ で積分したものとなる．

　式中の各自由粒子核

K_{0}

を, 式 (6-66) と同様に無摂動ハミルトニアン

H_{0}

の固有関数を用いて表わすならば次となる：

\begin{aligned} K_{0} (2, 4) & = K_{U} (2, 4) = \sum_{m} ϕ_{m} (x_{2}) ϕ_{m}^{*} (x_{4}) e^{- i E_{m} (t_{2} - t_{4})} [t_{2} > t_{4}], \\ (2) & K_{0} (4, 3) & = K_{U} (4, 3) = \sum_{k} ϕ_{k} (x_{4}) ϕ_{k}^{*} (x_{3}) e^{- i E_{k} (t_{4} - t_{3})} [t_{4} > t_{3}], \\ K_{0} (3, 1) & = K_{U} (3, 1) = \sum_{n} ϕ_{n} (x_{3}) ϕ_{n}^{*} (x_{1}) e^{- i E_{n} (t_{3} - t_{1})} [t_{3} > t_{1}] \end{aligned}

　これらを上式(1)に代入すると,

\begin{aligned} K_{V}^{(2)} (2, 1) = {(- \frac{i}{ℏ})}^{2} \int_{- \infty}^{\infty} d x_{4} \int_{t_{1}}^{t_{2}} d t_{4} \int_{- \infty}^{\infty} d x_{3} \int_{t_{1}}^{t_{4}} d t_{3} \sum_{m} \sum_{k} \sum_{n} ϕ_{m} (x_{2}) ϕ_{m}^{*} (x_{4}) \\ \times e^{- i E_{m} (t_{2} - t_{4})} V (4) ϕ_{k} (x_{4}) ϕ_{k}^{*} (x_{3}) e^{- i E_{k} (t_{4} - t_{3})} V (3) ϕ_{n} (x_{3}) ϕ_{n}^{*} (x_{1}) e^{- i E_{n} (t_{3} - t_{1})} \\ = - \frac{1}{ℏ^{2}} \sum_{m} \sum_{n} ϕ_{m} (x_{2}) ϕ_{n}^{*} (x_{1}) \int_{t_{1}}^{t_{2}} d t_{4} \int_{t_{1}}^{t_{4}} d t_{3} \sum_{k} e^{- i E_{m} (t_{2} - t_{4})} \\ \times \int_{- \infty}^{\infty} d x_{4} ϕ_{m}^{*} (x_{4}) V (4) ϕ_{k} (x_{4}) e^{- i E_{k} (t_{4} - t_{3})} \int_{- \infty}^{\infty} d x_{3} ϕ_{k}^{*} (x_{3}) V (3) ϕ_{n} (x_{3}) e^{- i E_{n} (t_{3} - t_{1})} \\ = \sum_{m} \sum_{n} ϕ_{m} (x_{2}) ϕ_{n}^{*} (x_{1}) [- \frac{1}{ℏ^{2}} \int_{t_{1}}^{t_{2}} d t_{4} \int_{t_{1}}^{t_{4}} d t_{3} \sum_{k} e^{- i E_{m} (t_{2} - t_{4}) / ℏ} V_{m k} (t_{4}) e^{- i E_{k} (t_{4} - t_{3}) / ℏ} \\ \times V_{k n} (t_{3}) e^{- i E_{n} (t_{3} - t_{1}) / ℏ}] \\ (3) & \equiv \sum_{m} \sum_{n} λ_{m n}^{(2)} (t_{2}, t_{1}) ϕ_{m} (x_{2}) ϕ_{n}^{*} (x_{1}) \end{aligned}

従って

λ_{m n}^{(2)}

は確かに式 (6-74) の形になっている：

\begin{matrix} (4) & λ_{m n}^{(2)} (t_{2}, t_{1}) = - \frac{1}{ℏ^{2}} \int_{t_{1}}^{t_{2}} d t_{4} \int_{t_{1}}^{t_{4}} d t_{3} \sum_{k} e^{- i E_{m} (t_{2} - t_{4}) / ℏ} V_{m k} (t_{4}) e^{- i E_{k} (t_{4} - t_{3}) / ℏ} V_{k n} (t_{3}) e^{- i E_{n} (t_{3} - t_{1}) / ℏ} \end{matrix}

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31