問題 6-18 の解答例

Problem 6-18

Derive and interpret the integral equation

\begin{matrix} (6-75) & λ_{m n} (t_{2}, t_{1}) = δ_{m n} e^{- i E_{m} (t_{2} - t_{1}) / ℏ} - \frac{i}{ℏ} \int_{t_{1}}^{t_{2}} d t_{3} e^{- i E_{m} (t_{2} - t_{3}) / ℏ} \sum_{k} V_{m k} (t_{3}) λ_{k n} (t_{3}, t_{1}) \end{matrix}

(解答)　式 (6-17) の $K_{V}$ は式 (6-19) のように書くことが出来るのであった：

\begin{matrix} (6.19) & K_{V} (b, a) = K_{0} (b, a) - \frac{i}{ℏ} \int d τ_{c} K_{0} (b, c) V (c) K_{V} (c, a) \end{matrix}

この式 (6-19) の持つ物理的意味は § 6.2 に次のように記述されている：
「

a

から

b

への系の遷移に対する全振幅は, 散乱の数がいくらあっても2つの選択肢の和で表される． 1つの選択肢は散乱なしに遷移が起こる振幅であり

K_{0}

と表される． 2番目の選択肢は1つ以上の散乱によって遷移が起こる振幅であり, 式(6-19)の第2項で表される．この第2項の点

c

は最後の散乱が起こった点であると考えることが出来る．ポテンシャル場の中で系は

a

から

c

へ運動するが, その運動は

K_{V} (c, a)

によって厳密に記述される．そして点

c

において最後の散乱が起こり,その後系は自由な系として(散乱を受けないで)点

b

に到る．この運動は

K_{0}

によって表される」．
そして, この解釈は本文の図6-3 に示されている：

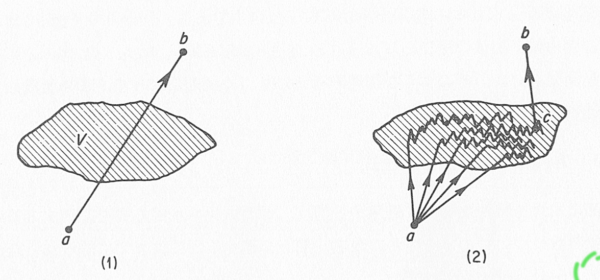
図 6-3. (1) では, 粒子は自由粒子としてポテンシャルを通過して $a$ から $b$ まで動く．この振幅は $K_{0} (b, a)$ である． (2)では, 粒子は $V$ によって1回以上散乱される．最後の散乱は $c$ で起こる． $a$ から $c$ への運動は $K_{V} (c, a)$ によって記述され， $c$ から $b$ への運動は $K_{0} (b, c)$ によって記述される． $c$ のあらゆる位置が考慮されるときに, (1) と (2) の状況を組み合わせたものは, あらゆる可能な場合を尽くすことになり， $K_{V} (b, a)$ は式(6.19)の形で与えられる．

このとき, 自由粒子核を $K_{U}$ とするならば上式は次のように表せる：

\begin{matrix} (1) & K_{V} (2, 1) = K_{U} (2, 1) - \frac{i}{ℏ} \int d x_{3} \int_{t_{1}}^{t_{2}} d t_{3} K_{U} (2, 3) V (3) K_{V} (3, 1) \end{matrix}

この式 (1) で, 自由粒子核

K_{U}

を式 (6-66) の形に, そして

K_{V} (3, 1)

に式 (6-68) の形を用いる：

\begin{aligned} (6-66) & K_{U} (2, 1) & = \sum_{n} ϕ_{n} (x_{2}) ϕ_{n}^{*} (x_{1}) e^{- i E_{n} (t_{2} - t_{1}) / ℏ}, K_{U} (2, 3) = \sum_{m} ϕ_{m} (x_{2}) ϕ_{m}^{*} (x_{3}) e^{- i E_{m} (t_{2} - t_{3}) / ℏ}, \\ (6-68) & K_{V} (3, 1) & = \sum_{n} \sum_{k} λ_{k n} (t_{3}, t_{1}) ϕ_{k} (x_{3}) ϕ_{n}^{*} (x_{1}) \end{aligned}

すると, 式 (1) は

V_{m k}

の定義式 (6-71) も用いることで次のように書くことが出来る：

\begin{aligned} K_{V} (2, 1) = \sum_{n} ϕ_{n} (x_{2}) ϕ_{n}^{*} (x_{1}) e^{- i E_{n} (t_{2} - t_{1}) / ℏ} \\ - \frac{i}{ℏ} \int d x_{3} \int_{t_{1}}^{t_{2}} d t_{3} \sum_{m} ϕ_{m} (x_{2}) ϕ_{m}^{*} (x_{3}) e^{- i E_{m} (t_{2} - t_{3}) / ℏ} V (3) \sum_{n} \sum_{k} λ_{k n} (t_{3}, t_{1}) ϕ_{k} (x_{3}) ϕ_{n}^{*} (x_{1}) \\ = \sum_{n} \sum_{m} δ_{m n} e^{- i E_{m} (t_{2} - t_{1}) / ℏ} ϕ_{m} (x_{2}) ϕ_{n}^{*} (x_{1}) \\ - \frac{i}{ℏ} \sum_{m} \sum_{n} \int_{t_{1}}^{t_{2}} d t_{3} e^{- i E_{m} (t_{2} - t_{3}) / ℏ} \sum_{k} \underset{V_{m k} (t_{3})}{\underset{⏟}{\int d x_{3} ϕ_{m}^{*} (x_{3}) V (3) ϕ_{k} (x_{3})}} λ_{k n} (t_{3}, t_{1}) ϕ_{m} (x_{2}) ϕ_{n}^{*} (x_{1}) \\ (2) & = \sum_{n} \sum_{m} {δ_{m n} e^{- i E_{m} (t_{2} - t_{1}) / ℏ} - \frac{i}{ℏ} \int_{t_{1}}^{t_{2}} d t_{3} e^{- i E_{m} (t_{2} - t_{3}) / ℏ} \sum_{k} V_{m k} (t_{3}) λ_{k n} (t_{3}, t_{1})} ϕ_{m} (x_{2}) ϕ_{n}^{*} (x_{1}) \\ (3) & \equiv \sum_{n} \sum_{m} λ_{m n} (t_{2}, t_{1}) ϕ_{m} (x_{2}) ϕ_{n}^{*} (x_{1}) \end{aligned}

このとき, 前段の式(2)の

{}

中が, 最終式(3)の

λ_{m n} (t_{2}, t_{1})

であることは明らかである．よって,

\begin{matrix} (3) & λ_{m n} (t_{2}, t_{1}) = δ_{m n} e^{- i E_{m} (t_{2} - t_{1}) / ℏ} - \frac{i}{ℏ} \int_{t_{1}}^{t_{2}} d t_{3} e^{- i E_{m} (t_{2} - t_{3}) / ℏ} \sum_{k} V_{m k} (t_{3}) λ_{k n} (t_{3}, t_{1}) \end{matrix}

この式 (3) が示す物理的意味は上述の式(6-19)と同じである．すなわち, 終状態の波動関数

ψ (x_{2}, t_{2})

を無摂動ハミルトニアンの固有関数

ϕ (x_{2})

で展開したとき

λ_{m n}

を用いて,

\begin{matrix} (4) & ψ (x_{2}, t_{2}) = \sum_{m} λ_{m n} (t_{2}, t_{1}) ϕ_{m} (x_{2}) \end{matrix}

と表せるのであったから, これに式(3)の

λ_{m n}

を代入するならば,

\begin{aligned} ψ (x_{2}, t_{2}) & = \sum_{m} δ_{m n} ϕ_{m} (x_{2}) e^{- i E_{m} (t_{2} - t_{1}) / ℏ} - \sum_{m} \frac{i}{ℏ} \int_{t_{1}}^{t_{2}} d t_{3} e^{- i E_{m} (t_{2} - t_{3}) / ℏ} \sum_{k} V_{m k} (t_{3}) λ_{k n} (t_{3}, t_{1}) ϕ_{m} (x_{2}) \\ (5) & \equiv ϕ_{n} (x_{2}) e^{- i E_{n} (t_{2} - t_{1}) / ℏ} + \sum_{m} λ_{m n} (t_{2}, t_{1}) ϕ_{m} (x_{2}) \end{aligned}

となる．このとき第1項目は散乱を受けずに状態

n

に留まる確率振幅であり, 第2項目は散乱を受けて他の状態

m

たちへ遷移する確率振幅すなわち「遷移振幅」である．
ただし, 第2項目に於ける状態

n

に見出される振幅すなわち「

m = n

のときの遷移振幅

λ_{n n}

」というのは, 本文で後述されているように「ポテンシャル

V

による状態

n

からの散乱が可能な振幅と解釈するべき」である．

月	火	水	木	金	土	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31