Problem 9-2
Explain why the charge density corresponding to a single charge
Show that
Explain why the currrent density is
If we have a number of charges
If the expansions of
then, using Eqs. (9-9) and (9-7), the expansion coefficients satisfy
From Eqs. (9-8) and (9-10), the coefficient of expansion of
so we have
or,
The function
( 解答 ) 問題文で与えられている電荷密度の式 (1) を全空間で体積積分すると, ディラックの3次元の「デルタ関数」の性質
を利用して,「時刻
次に, 式 (9-14) 中の
ここでディラックの「デルタ関数」の3次元に於ける表現式は,
である.これを利用すると,
となり, 問題文の電荷密度の式に一致した結果が得られるからである.
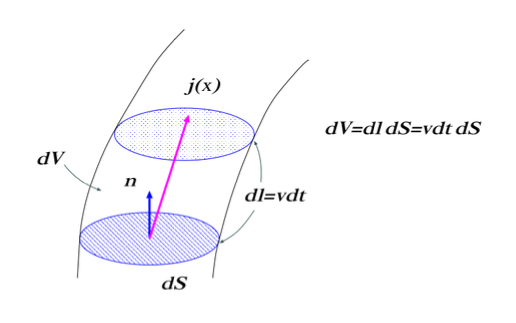
次に電流密度について考える.電流密度は次で定義できる:
何故なら, 微小体積
従って, 微小面積
従って, この電流密度の表現
多くの電荷が存在する場合には, 式(9-14) 中に, 今度は式 (9-16) を代入して見れば良い.
まず, 電荷密度
電流密度
【 参考 】 式 (3) 以降は問題文には含まれない式とは思われるが, それらも導出しておこう.
まず, 式 (3) 及び式 (4) が言えることを示す.そのために, 次のベクトル解析の公式を利用する:
この公式に於いて
式 (9-7):
この結果と, 式 (3):
式 (9-9) から
従って
この結果と式 (3):
また, 式 (3):
そして, 式 (9-14) の
以上の結果式(27) と式 (28) を, 次の式 (9-10):
に代入すると,
この結果式 (29) と式 (30) を比較する.また, 式 (9-13) を時間微分すると
この式 (31) すなわち式 (9-17) から,
となるので, 例えば