特殊相対性理論の原理と結果の要約
\(\textit{Seventh Lecture}\)
相対性の原理とは, 関係する全ての物体が一緒に一様な速度 \(v\) で動いている場合, 全ての物理現象はまったく同じに見えるという原理である．つまり, (例えば宇宙の物質の重心に対して) 速度 \(v\) で一様に動いている閉じた宇宙船の中だけで行われた実験では, この速度 \(v\) を決定することは出来ない．この原理は実験的に検証されている．ニュートンの法則はこの原理を満たしている．次のガリレオ変換を受けても変わらないからである：
\begin{equation}
x’=x-vt,\quad y’=y,\quad z’=z,\quad t’=t
\tag{2.7.1}
\end{equation}
x’=x-vt,\quad y’=y,\quad z’=z,\quad t’=t
\tag{2.7.1}
\end{equation}
なぜなら, ニュートンの法則に含まれているのは2階微分だけだからである．しかし, マクスウェル方程式はこの変換を受けると変化し, この分野の初期の研究者はこの特徴を利用して地球の速度の絶対決定を試みた(マイケルソン-モーリー実験)．しかしこの種の効果を検出できなかったため, 最終的にアインシュタインは「マクスウェル方程式はどの座標系でも同じ形であり, 特に光の速度はどの座標系でも同じである」という仮説を立てた．マクスウェル方程式を不変にする座標系間の変換は, 次のローレンツ変換である：
\begin{align}
x’&=\frac{x-vt}{\sqrt{1-(v^{2}/c^{2})}}=x\cosh u – ct \sinh u,\notag\\
y’&=y,\qquad z’=z,\notag\\
t’&=\frac{t-(xv/c^{2})}{\sqrt{1-(v^{2}/c^{2})}}=-\frac{x}{c}\sinh u + t\cosh u
\tag{2.7.2}
\end{align}
x’&=\frac{x-vt}{\sqrt{1-(v^{2}/c^{2})}}=x\cosh u – ct \sinh u,\notag\\
y’&=y,\qquad z’=z,\notag\\
t’&=\frac{t-(xv/c^{2})}{\sqrt{1-(v^{2}/c^{2})}}=-\frac{x}{c}\sinh u + t\cosh u
\tag{2.7.2}
\end{align}
ただし \(\tanh u = v/c\) である [1][訳註] 式 (2.7.3) のように書き表した場合では \(\tan\theta =i\beta=i(v/c)\) となる．本文では「以後では, 光速 \(c\) が \(1\) … Continue reading ．
式の後半の形は, 座標軸の回転の式
\begin{align}
x’ &= x \cos\theta + y \sin\theta,\notag\\
y’ & = -x \sin\theta + y \cos\theta
\tag{2.7.3}
\end{align}
x’ &= x \cos\theta + y \sin\theta,\notag\\
y’ & = -x \sin\theta + y \cos\theta
\tag{2.7.3}
\end{align}
との類似性を示すために書いたものである．連続した変換 \(v_1\) と \(v_2\) あるいは \(u_1\) と \(u_2\) の足し合わせというのは, 単一の変換 \(v_3\) または \(u_3\) が
\begin{equation}
v_3=v_1+v_2,\qquad \mathrm{or}\qquad \tanh u_3 = \tanh (u_1+u_2)
\tag{2.7.4}
\end{equation}
v_3=v_1+v_2,\qquad \mathrm{or}\qquad \tanh u_3 = \tanh (u_1+u_2)
\tag{2.7.4}
\end{equation}
であるならば, それは同じ最終系を与えるという意味である [2][訳註] 最初の式は, 相対論的な速度の合成則 \[v_3=\frac{v_1+v_2}{\ds{1+\frac{v_1v_2}{c^2}}}\]とすべきではないかと思われる?!．後の式は, それぞれの速度 \(v_1, … Continue reading．アインシュタインは「ニュートンの法則は, ローレンツ変換の下でも形が変わらないように修正されなければならない」と仮定した(特殊相対性理論)．
ローレンツ変換の興味深い結果は,「動いている系では時計の針が遅く見える」ことである．ある座標系から別の座標系への変換には「テンソル解析」を使うと便利である．この目的のために \(x,y,z,ct\) と同じように変換する4つの量の集合として \(4\)-ベクトルを定義する．添え字の \(\mu\) は4成分のどれを考えているかを示すために使われる．例えば,
\begin{equation}
x^{\,\mu}\quad \rightarrow\quad x^0= ct,\quad x^1=x,\quad x^2=y,\quad x^3=z
\tag{2.7.5}
\end{equation}
x^{\,\mu}\quad \rightarrow\quad x^0= ct,\quad x^1=x,\quad x^2=y,\quad x^3=z
\tag{2.7.5}
\end{equation}
次の量は \(4\)-ベクトルである： [3][訳注] 原書では反変ベクトルも共変ベクトルも区別なく共に下付きの添字で表現しており， 4元勾配は \(\nabla_{\mu}\) と表している．しかしここでは, … Continue reading
\begin{align}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\partial^{\,\mu}&=\pdiff{x_{\mu}}=\left(\frac{\partial}{c\partial t},\ -\pdiff{x},\ -\pdiff{y},\ -\pdiff{z}\right)
=\left(\frac{\partial}{c\partial t},\ -\nabla\right)\qquad
\mathrm{four\!-\!dimensional\ grandient}\notag\\
j^{\,\mu} &= \bigl(c\rho,\ j_x,\ j_y,\ j_z\bigr)=\left(c\rho,\ \mb{j}\right) \qquad
\mathrm{current(and\ charge)\,density}\notag\\
A^{\,\mu} &= \bigl(\phi,\ A_x,\ A_y,\ A_z\bigr)=\bigl(\phi,\ \mb{A}\bigr)
\qquad \mathrm{vector(and\ scalar)\ potential}\notag\\
p^{\,\mu} &= \left(\frac{E}{c},\ p_x,\ p_y,\ p_z\right)=\left(\frac{E}{c},\ \mb{p}\right)\qquad
\mathrm{momentum\ and total\ energy}
\tag{2.7.6}
\end{align}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\Bpdiff#1{\frac{\partial^{2}}{\partial #1^{2}}}
\def\mb#1{\mathbf{#1}}
\def\mr#1{\mathrm{#1}}
\def\reverse#1{\frac{1}{#1}}
\def\ds#1{\mbox{${\displaystyle\strut #1}$}}
\partial^{\,\mu}&=\pdiff{x_{\mu}}=\left(\frac{\partial}{c\partial t},\ -\pdiff{x},\ -\pdiff{y},\ -\pdiff{z}\right)
=\left(\frac{\partial}{c\partial t},\ -\nabla\right)\qquad
\mathrm{four\!-\!dimensional\ grandient}\notag\\
j^{\,\mu} &= \bigl(c\rho,\ j_x,\ j_y,\ j_z\bigr)=\left(c\rho,\ \mb{j}\right) \qquad
\mathrm{current(and\ charge)\,density}\notag\\
A^{\,\mu} &= \bigl(\phi,\ A_x,\ A_y,\ A_z\bigr)=\bigl(\phi,\ \mb{A}\bigr)
\qquad \mathrm{vector(and\ scalar)\ potential}\notag\\
p^{\,\mu} &= \left(\frac{E}{c},\ p_x,\ p_y,\ p_z\right)=\left(\frac{E}{c},\ \mb{p}\right)\qquad
\mathrm{momentum\ and total\ energy}
\tag{2.7.6}
\end{align}
「不変量」(invariant)とは, ローレンツ変換の下で変化しない量をいう．もし \(a^{\,\mu}\) と \(b^{\,\mu}\) が2つの \(4\)-ベクトルならば, 次の「スカラー積」(scalar product)は不変量である：
\begin{equation}
a\cdot b \equiv \sum_{\mu} a^{\,\mu}b_{\mu}=\eta_{\mu\nu} a^{\,\mu}b^{\,\nu}
=a^0 b_0-a^1 b_1-a^2 b_2-a^3 b_3=a^0 b^0-\mb{a}\cdot\mb{b}
\tag{2.7.7}
\end{equation}
a\cdot b \equiv \sum_{\mu} a^{\,\mu}b_{\mu}=\eta_{\mu\nu} a^{\,\mu}b^{\,\nu}
=a^0 b_0-a^1 b_1-a^2 b_2-a^3 b_3=a^0 b^0-\mb{a}\cdot\mb{b}
\tag{2.7.7}
\end{equation}
和の記号を書かないようにするため, 以下のような「和の規則」(summation convenction)を使用する．すなわち「同じ添字が２回出現する場合は, 第1, 第2, 第3成分の前にマイナス符号を付けて和をとる」．「連続方程式」(continuity equation)のローレンツ不変性は, ４-ベクトル \(\partial^{\,\mu}\) と \(j_{\mu}\) の「積」として書くことで簡単に証明できる：
\begin{align}
\mathrm{Div}\, j = \partial^{\,\mu}j_{\mu}&=\partial^{\,0}j_0+\partial^{\,1}j_1 +\partial^{\,2}j_2 +\partial^{\,3}j_3
=\frac{\partial}{c\partial t}c\rho-\pdiff{x}(-j_x) -\pdiff{y}(-j_y) -\pdiff{z}(-j_z)\notag\\
&=\ppdiff{\rho}{t} +\ppdiff{j_x}{x} +\ppdiff{j_y}{y} +\ppdiff{j_z}{z}\notag\\
&=\ppdiff{\rho}{t}+\mathrm{div}\,\mb{j}=0
\tag{2.7.8}
\end{align}
\mathrm{Div}\, j = \partial^{\,\mu}j_{\mu}&=\partial^{\,0}j_0+\partial^{\,1}j_1 +\partial^{\,2}j_2 +\partial^{\,3}j_3
=\frac{\partial}{c\partial t}c\rho-\pdiff{x}(-j_x) -\pdiff{y}(-j_y) -\pdiff{z}(-j_z)\notag\\
&=\ppdiff{\rho}{t} +\ppdiff{j_x}{x} +\ppdiff{j_y}{y} +\ppdiff{j_z}{z}\notag\\
&=\ppdiff{\rho}{t}+\mathrm{div}\,\mb{j}=0
\tag{2.7.8}
\end{align}
ある系で電荷が保存される場合, すべての系で電荷が保存されるのは, この「積」である4次元の発散 \(\mathrm{Div}\, j\) の不変性の結果である．もう一つの不変量は,
\begin{equation}%(2.7.9)
p^{\,\mu}p_{\mu}=p\cdot p =\frac{E^{2}}{c^{2}}-\mb{p}^{2}=m^{2}c^{2}
\tag{2.7.9}
\end{equation}
p^{\,\mu}p_{\mu}=p\cdot p =\frac{E^{2}}{c^{2}}-\mb{p}^{2}=m^{2}c^{2}
\tag{2.7.9}
\end{equation}
ただし \(E\) は「全エネルギー」， \(m\) は「静止質量」， \(mc^{2}\) は「静止エネルギー」, そして \(\mb{p}\) は「運動量」である．従って,
\begin{equation}
E^{2}=\mb{p}^{2}c^{2}+m^{2}c^{4}
\tag{2.7.10}
\end{equation}
E^{2}=\mb{p}^{2}c^{2}+m^{2}c^{4}
\tag{2.7.10}
\end{equation}
興味深いことに, 自由粒子の波動関数 \(\exp[-(i/\hbar)(Et-\mb{p}\cdot\mb{x})]\) の位相も不変量である．なぜなら,
\begin{equation}
p\cdot x=p^{\,\mu}x_{\mu}=\left(\frac{E}{c},\ \mb{p}\right)\cdot\bigl(ct,-\mb{x}\bigr)
=Et-\mb{p}\cdot\mb{x}
\tag{2.7.11}
\end{equation}
p\cdot x=p^{\,\mu}x_{\mu}=\left(\frac{E}{c},\ \mb{p}\right)\cdot\bigl(ct,-\mb{x}\bigr)
=Et-\mb{p}\cdot\mb{x}
\tag{2.7.11}
\end{equation}
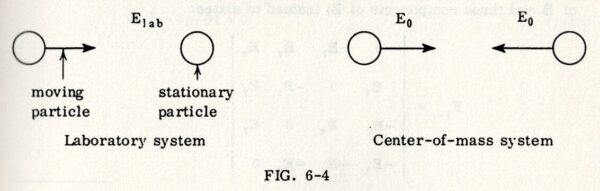
\(p^{\,\mu}p_{\mu}\) の不変性を利用すると, 次のようにして実験室系エネルギー\(E_{\mr{lab}}\) の重心系エネルギー \(E_0\) への変換が簡単に行える(簡単のために同一粒子を考える．下の図 6-4 を参照のこと.)：
\begin{align}
&p_{\,1}=\left(\frac{E_{\mr{lab}}}{c},\,\mb{p}\right),\quad p_{\,2}=\left(\frac{mc^{2}}{c},\,0\right),
\quad p’_{1}=\left(\frac{E_0}{c},\,\mb{p}_0\right),\quad p’_{2}=\left(\frac{E_0}{c},\,-\mb{p}_0\right),\notag\\
\rightarrow\quad & p_1\cdot p_2 =p_{1\mu}\,p^{\,\mu}_2=\left(\frac{E_{\mr{lab}}}{c},\,-\mb{p}\right)\cdot
\left(\frac{mc^{2}}{c},\,0\right)= E_{\mr{lab}}m,\notag\\
& p’_1\cdot p’_2 =p’^{\,\mu}_1 p’_{2\,\mu}
=\left(\frac{E_0}{c},\,\mb{p}_0\right)\cdot\left(\frac{E_0}{c},\,\mb{p}_0\right)
=\frac{E_0^{2}}{c^{2}}+\mb{p}_0^{2},\tag{2.7.12}\\
\mr{and}\quad &\frac{E_0^{2}}{c^{2}}=\mb{p}_0^{2}+m^{2}c^{2},\quad\rightarrow\quad
\mb{p}_0^{2}=\frac{E_0^{2}}{c^{2}}-m^{2}c^{2}
\tag{2.7.9-a}
\end{align}
&p_{\,1}=\left(\frac{E_{\mr{lab}}}{c},\,\mb{p}\right),\quad p_{\,2}=\left(\frac{mc^{2}}{c},\,0\right),
\quad p’_{1}=\left(\frac{E_0}{c},\,\mb{p}_0\right),\quad p’_{2}=\left(\frac{E_0}{c},\,-\mb{p}_0\right),\notag\\
\rightarrow\quad & p_1\cdot p_2 =p_{1\mu}\,p^{\,\mu}_2=\left(\frac{E_{\mr{lab}}}{c},\,-\mb{p}\right)\cdot
\left(\frac{mc^{2}}{c},\,0\right)= E_{\mr{lab}}m,\notag\\
& p’_1\cdot p’_2 =p’^{\,\mu}_1 p’_{2\,\mu}
=\left(\frac{E_0}{c},\,\mb{p}_0\right)\cdot\left(\frac{E_0}{c},\,\mb{p}_0\right)
=\frac{E_0^{2}}{c^{2}}+\mb{p}_0^{2},\tag{2.7.12}\\
\mr{and}\quad &\frac{E_0^{2}}{c^{2}}=\mb{p}_0^{2}+m^{2}c^{2},\quad\rightarrow\quad
\mb{p}_0^{2}=\frac{E_0^{2}}{c^{2}}-m^{2}c^{2}
\tag{2.7.9-a}
\end{align}
式 (2.7.12) に式 (2.7.9-a) を代入すると,
\begin{equation*}
p_1’\cdot p’_2 =\frac{E_0^{2}}{c^{2}}+\mb{p}_0^{2}=\frac{E_0^{2}}{c^{2}}+\left(\frac{E_0^{2}}{c^{2}}-m^{2}c^{2}\right)
=2\frac{E_0^{2}}{c^{2}}-m^{2}c^{2}
\end{equation*}
p_1’\cdot p’_2 =\frac{E_0^{2}}{c^{2}}+\mb{p}_0^{2}=\frac{E_0^{2}}{c^{2}}+\left(\frac{E_0^{2}}{c^{2}}-m^{2}c^{2}\right)
=2\frac{E_0^{2}}{c^{2}}-m^{2}c^{2}
\end{equation*}
\(p_1\cdot p_2 = p’_1\cdot p’_2\) であるから,
\begin{equation}
E_{\mr{lab}}m=2\frac{E_0^{2}}{c^{2}}-m^{2}c^{2},\quad\rightarrow\quad
E_0=\sqrt{\frac{1}{2}mc^{2}(E_{\mr{lab}}+mc^{2})}
\tag{2.7.13}
\end{equation}
E_{\mr{lab}}m=2\frac{E_0^{2}}{c^{2}}-m^{2}c^{2},\quad\rightarrow\quad
E_0=\sqrt{\frac{1}{2}mc^{2}(E_{\mr{lab}}+mc^{2})}
\tag{2.7.13}
\end{equation}
図. 6-4
電磁気学の方程式 \(\mb{B}=\nabla\times\mb{A}\) と \(\displaystyle \mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t}-\nabla \phi\) は, 容易にテンソル表記に書かれる．\(\displaystyle \partial_{\,\mu}=\left(\frac{\partial}{c\partial t},\,\nabla\right)\) そして \(A_{\mu}=(\phi,-\mb{A})\) に注意すると, [4][訳注] ランダウ：「力学・場の理論」を参照のこと．そこで用いられている計量テンソルは \(\eta^{\mu\nu}=(+1,-1,-1,-1)\) である．
\begin{align}
B_x &=\ppdiff{A_z}{y}-\ppdiff{A_y}{z}=\partial_2 (-A_3) – \partial_3 (-A_2)
=-\bigl(\partial_2 A_3 – \partial_3 A_2\bigr)= -F_{23},\notag\\
B_y &=\ppdiff{A_x}{z}-\ppdiff{A_z}{x}=\partial_3 (-A_1) – \partial_1 (-A_3)
=-\left(\partial_3 A_1-\partial_1 A_3\right)=-F_{31},\notag\\
B_z &=\ppdiff{A_y}{x}-\ppdiff{A_x}{y}=\partial_1 (-A_2) – \partial_2 (-A_1)
=-\left(\partial_{1}A_2-\partial_{2}A_1\right)=-F_{12},\notag\\
E_x &=-\frac{1}{c}\ppdiff{A_x}{t}-\ppdiff{\phi}{x}
=\frac{1}{c}\pdiff{t}(-A_x)-\pdiff{x}\phi
=\partial_0 A_1 -\partial_1 A_0=F_{01},\notag\\
E_y &=-\frac{1}{c}\ppdiff{A_y}{t}-\ppdiff{\phi}{y}=\partial_0 A_2 -\partial_2 A_0=F_{02},\notag\\
E_z &=-\frac{1}{c}\ppdiff{A_z}{t}-\ppdiff{\phi}{z}=\partial_0 A_3 -\partial_3 A_0=F_{03}
\tag{2.7.14}
\end{align}
B_x &=\ppdiff{A_z}{y}-\ppdiff{A_y}{z}=\partial_2 (-A_3) – \partial_3 (-A_2)
=-\bigl(\partial_2 A_3 – \partial_3 A_2\bigr)= -F_{23},\notag\\
B_y &=\ppdiff{A_x}{z}-\ppdiff{A_z}{x}=\partial_3 (-A_1) – \partial_1 (-A_3)
=-\left(\partial_3 A_1-\partial_1 A_3\right)=-F_{31},\notag\\
B_z &=\ppdiff{A_y}{x}-\ppdiff{A_x}{y}=\partial_1 (-A_2) – \partial_2 (-A_1)
=-\left(\partial_{1}A_2-\partial_{2}A_1\right)=-F_{12},\notag\\
E_x &=-\frac{1}{c}\ppdiff{A_x}{t}-\ppdiff{\phi}{x}
=\frac{1}{c}\pdiff{t}(-A_x)-\pdiff{x}\phi
=\partial_0 A_1 -\partial_1 A_0=F_{01},\notag\\
E_y &=-\frac{1}{c}\ppdiff{A_y}{t}-\ppdiff{\phi}{y}=\partial_0 A_2 -\partial_2 A_0=F_{02},\notag\\
E_z &=-\frac{1}{c}\ppdiff{A_z}{t}-\ppdiff{\phi}{z}=\partial_0 A_3 -\partial_3 A_0=F_{03}
\tag{2.7.14}
\end{align}
ただし \(4\)-ベクトル \(A^{\,\mu}\) の第 \(0\) 成分が \(\phi\) であることを利用している．以上のことから, 電場と磁場の成分 \(B_x\,\), \(B_y\,\), \(B_z\,\), \(E_x\,\), \(E_y\,\), \(E_z\) は次の2階テンソル \(F_{\mu\nu}\) の成分であることが分かる：
\begin{equation}
F_{\mu\nu}=\ppdiff{A_\nu}{x^{\,\mu}}-\ppdiff{A_\mu}{x^{\,\nu}}=\partial_{\mu}A_\nu -\partial_{\nu} A_{\mu},
\quad \mathrm{or}\quad F^{\mu\nu}=\partial^{\mu}A^{\nu} -\partial^{\nu} A^{\mu}
\tag{2.7.15}
\end{equation}
F_{\mu\nu}=\ppdiff{A_\nu}{x^{\,\mu}}-\ppdiff{A_\mu}{x^{\,\nu}}=\partial_{\mu}A_\nu -\partial_{\nu} A_{\mu},
\quad \mathrm{or}\quad F^{\mu\nu}=\partial^{\mu}A^{\nu} -\partial^{\nu} A^{\mu}
\tag{2.7.15}
\end{equation}
このテンソルは反対称 (\(F_{\mu\nu}=-F_{\nu\mu}\)) で対角成分 (\(\mu=\nu\)) はゼロである．従って16個の成分の内, 独立な成分は6個だけ(\(\mb{E}\) の3成分と \(\mb{B}\) の3成分)である．
\begin{equation}
F_{\mu\nu}=\begin{bmatrix} 0 & E_x & E_y & E_z \\ -E_x & 0 & -B_z & B_y \\ -E_y & B_z & 0 & -B_x \\
-E_z & -B_y & B_x & 0 \end{bmatrix}
\tag{2.7.16}
\end{equation}
F_{\mu\nu}=\begin{bmatrix} 0 & E_x & E_y & E_z \\ -E_x & 0 & -B_z & B_y \\ -E_y & B_z & 0 & -B_x \\
-E_z & -B_y & B_x & 0 \end{bmatrix}
\tag{2.7.16}
\end{equation}
マックスウェル方程式の第2の組は, 4-ベクトルの表現で次のように書かれる：
\begin{equation}
\nabla\times\mb{B}=\frac{1}{c}\ppdiff{\mb{E}}{t}+\frac{4\pi}{c}\mb{J},\quad \nabla\cdot\mb{E}=4\pi\rho \quad\rightarrow
\quad \partial^{\,\mu}F_{\mu\nu}=\frac{4\pi}{c} j_{\nu}
\tag{2.7.17}
\end{equation}
\nabla\times\mb{B}=\frac{1}{c}\ppdiff{\mb{E}}{t}+\frac{4\pi}{c}\mb{J},\quad \nabla\cdot\mb{E}=4\pi\rho \quad\rightarrow
\quad \partial^{\,\mu}F_{\mu\nu}=\frac{4\pi}{c} j_{\nu}
\tag{2.7.17}
\end{equation}
ただし \(\nu=0,1,2,3\) であり, 和添字 \(\mu\) はダミーである [5][訳注] 4元ベクトル \(A^{\,\mu}\) の2乗は, 和の規則から \(A\cdot A=A^{\,\mu}A_{\mu}\) と書かれる． このとき, 同じ添字の対のうち一つは上に, … Continue reading．\(\nu=1,2,3\) は \(\mr{curl}\) 式の3成分であり \(\nu=0\) は発散の式を与える[6][訳注] \(\partial^{\,\mu}\) は反変ベクトルで \(\partial^{\,\mu}=(\partial/c\partial t,-\nabla)\) となることに注意すると, 例えば, … Continue reading．
ポテンシャル \(A_{\mu}\) が満たす式は, 式 (2.7.15) を式 (2.7.17) へ代入することで見出される：
\begin{equation}
\partial^{\,\mu} F_{\mu\nu}=\partial^{\,\mu} \bigl(\partial_{\mu}A_\nu -\partial_{\nu} A_{\mu}\bigr)
=\partial^{\,\mu}\partial_{\mu}A_\nu -\partial_{\nu}\partial^{\,\mu} A_{\mu}
=\frac{4\pi}{c} j_{\nu}
\tag{2.7.18}
\end{equation}
\partial^{\,\mu} F_{\mu\nu}=\partial^{\,\mu} \bigl(\partial_{\mu}A_\nu -\partial_{\nu} A_{\mu}\bigr)
=\partial^{\,\mu}\partial_{\mu}A_\nu -\partial_{\nu}\partial^{\,\mu} A_{\mu}
=\frac{4\pi}{c} j_{\nu}
\tag{2.7.18}
\end{equation}
しかしながら, ポテンシャル \(A_{\mu}\) は一意的ではない．なぜなら, 次のポテンシャルも上の関係を満たすからである：
\begin{equation}
A’_{\mu}=A_{\mu}-\partial_{\mu}\,\chi
\tag{2.7.19}
\end{equation}
A’_{\mu}=A_{\mu}-\partial_{\mu}\,\chi
\tag{2.7.19}
\end{equation}
ここで \(\chi\) は位置の任意関数である．(歴史的な理由で) ポテンシャルのこのような変化即ち変換は「ゲージ変換」と呼ばれる．ポテンシャルをより明確なものにするために, 全てのポテンシャルは次のいわゆる「ローレンツ条件」を満たすように変換されていると仮定しよう [7] これは \(A\) を完全に定義するには十分ではない．依然として \(\square^{2}\chi=0\) を満たすどんな \(\chi\) も用いることが出来る．：
\begin{equation}
\partial^{\,\mu} A_{\mu}=0
\tag{2.7.20-a}
\end{equation}
\partial^{\,\mu} A_{\mu}=0
\tag{2.7.20-a}
\end{equation}
これは便利な式である．なぜなら \(A_{\mu}\) の方程式 (2.7.18) を次式のように簡単化するからである：
\begin{equation}
\partial^{\,\mu} F_{\mu\nu}=\partial^{\,\mu}\partial_{\mu}A_\nu -\cancel{\partial_{\nu}\partial^{\,\mu} A_{\mu}}
=\partial^{\,\mu}\partial_{\mu}A_\nu=\frac{4\pi}{c} j_{\nu},\quad\rightarrow\quad \partial^{\,\mu}\partial_{\mu}A_\nu=\frac{4\pi}{c} j_{\nu}
\tag{2.7.21-a}
\end{equation}
\partial^{\,\mu} F_{\mu\nu}=\partial^{\,\mu}\partial_{\mu}A_\nu -\cancel{\partial_{\nu}\partial^{\,\mu} A_{\mu}}
=\partial^{\,\mu}\partial_{\mu}A_\nu=\frac{4\pi}{c} j_{\nu},\quad\rightarrow\quad \partial^{\,\mu}\partial_{\mu}A_\nu=\frac{4\pi}{c} j_{\nu}
\tag{2.7.21-a}
\end{equation}
この式は次の「波動方程式」であることが分かる：
\begin{align}
&\nabla^{2}\mb{A}-\frac{1}{c^{2}}\Bppdiff{\mb{A}}{t}=-\frac{4\pi}{c} \mb{j}, \tag{2.7.21-b}\\
&\nabla^{2} \phi -\frac{1}{c^{2}}\Bppdiff{\phi}{t}=-4\pi\rho \notag
\end{align}
&\nabla^{2}\mb{A}-\frac{1}{c^{2}}\Bppdiff{\mb{A}}{t}=-\frac{4\pi}{c} \mb{j}, \tag{2.7.21-b}\\
&\nabla^{2} \phi -\frac{1}{c^{2}}\Bppdiff{\phi}{t}=-4\pi\rho \notag
\end{align}
式 (2.7.21-a) は, 時には次のスカラー演算子である「ダランベール演算子」：
\begin{align}
\square^{2}&\equiv \eta^{\mu\nu}\pdiff{x^{\mu}}\pdiff{x^{\nu}}=\eta^{\mu\nu}\partial_{\mu}\partial_{\nu}
=\partial_{\mu}\partial^{\,\mu}
=\left(\frac{1}{c}\pdiff{t},\nabla\right)\cdot\left(\frac{1}{c}\pdiff{t},-\nabla\right)\notag\\
&=\frac{1}{c^{2}}\Bpdiff{t}-\nabla^{2}
\tag{2.7.22}
\end{align}
\square^{2}&\equiv \eta^{\mu\nu}\pdiff{x^{\mu}}\pdiff{x^{\nu}}=\eta^{\mu\nu}\partial_{\mu}\partial_{\nu}
=\partial_{\mu}\partial^{\,\mu}
=\left(\frac{1}{c}\pdiff{t},\nabla\right)\cdot\left(\frac{1}{c}\pdiff{t},-\nabla\right)\notag\\
&=\frac{1}{c^{2}}\Bpdiff{t}-\nabla^{2}
\tag{2.7.22}
\end{align}
を用いて次のように書かれる：
\begin{equation}
\square^{2}A_{\nu}=\frac{4\pi}{c} j_{\nu}\qquad\mathrm{or}\qquad
\square^{2}A^{\,\mu}=\frac{4\pi}{c} j^{\,\mu}
\tag{2.7.23}
\end{equation}
\square^{2}A_{\nu}=\frac{4\pi}{c} j_{\nu}\qquad\mathrm{or}\qquad
\square^{2}A^{\,\mu}=\frac{4\pi}{c} j^{\,\mu}
\tag{2.7.23}
\end{equation}
式 (2.7.20-a)：\(\partial^{\,\mu}A_{\mu}=0\) は「ローレンツ・ゲージ」と呼ばれ, 古典電磁気学では普通に選択されるゲージ条件である：
\begin{equation}
\partial^{\,\mu}A_{\mu}=\left(\frac{1}{c}\pdiff{t},-\nabla\right)\left(\phi,-\mb{A}\right)=
\frac{1}{c}\ppdiff{\phi}{t}+\nabla\cdot\mb{A}=0\quad\rightarrow\quad
\mathrm{div}\,\mb{A}+\frac{1}{c}\ppdiff{\phi}{t}=0
\tag{2.7.20-b}
\end{equation}
\partial^{\,\mu}A_{\mu}=\left(\frac{1}{c}\pdiff{t},-\nabla\right)\left(\phi,-\mb{A}\right)=
\frac{1}{c}\ppdiff{\phi}{t}+\nabla\cdot\mb{A}=0\quad\rightarrow\quad
\mathrm{div}\,\mb{A}+\frac{1}{c}\ppdiff{\phi}{t}=0
\tag{2.7.20-b}
\end{equation}
References
| ↑1 | [訳註] 式 (2.7.3) のように書き表した場合では \(\tan\theta =i\beta=i(v/c)\) となる．本文では「以後では, 光速 \(c\) が \(1\) となるような時間単位を使うことにする」とある．しかし「経路積分」に合わせて \(c\) はきちんと表示した式に書き直しておくことにする． |
|---|---|
| ↑2 | [訳註] 最初の式は, 相対論的な速度の合成則 \[v_3=\frac{v_1+v_2}{\ds{1+\frac{v_1v_2}{c^2}}}\]とすべきではないかと思われる?!．後の式は, それぞれの速度 \(v_1, v_2\) に対応した式 (2.7.3) で定義される回転角を \(\theta_1, \theta_2\) とするとき, 両速度を合成した \(v_3\) に対応する角度 \(\theta_3\) は \(\theta_1\) と \(\theta_2\) の単純な和 \(\theta_1+\theta_2\) になるという事実を言っている． |
| ↑3 | [訳注] 原書では反変ベクトルも共変ベクトルも区別なく共に下付きの添字で表現しており， 4元勾配は \(\nabla_{\mu}\) と表している．しかしここでは, 現代の教科書的に反変・共変ベクトルを添字の上下で区別する表現に書き直しておく．従って, 原書の 4-ベクトルの計量テンソル \(\eta^{\,\mu\nu}\) は \((+1,-1,-1,-1)\) であることに注意する．また, 4元ベクトルポテンシャル \(A^{\mu}\) は単位系によって時間成分が違ってくるので注意が必要である．例えば, 内山では MKS 単位系を用いているので, 式 (11.3) で \(A^{\mu}=(\phi/c,\mb{A})\) としている． |
| ↑4 | [訳注] ランダウ：「力学・場の理論」を参照のこと．そこで用いられている計量テンソルは \(\eta^{\mu\nu}=(+1,-1,-1,-1)\) である． |
| ↑5 | [訳注] 4元ベクトル \(A^{\,\mu}\) の2乗は, 和の規則から \(A\cdot A=A^{\,\mu}A_{\mu}\) と書かれる． このとき, 同じ添字の対のうち一つは上に, 他は下に付かなければならない．これらの添字は「ダミー指標」と言われる． |
| ↑6 | [訳注] \(\partial^{\,\mu}\) は反変ベクトルで \(\partial^{\,\mu}=(\partial/c\partial t,-\nabla)\) となることに注意すると, 例えば, 次となる： \begin{align*} &\partial^{\,\mu}F_{\mu 1}=\partial^{\,0}F_{01}+\partial^{\,1}F_{11}+\partial^{\,2}F_{21}+\partial^{\,3}F_{31} =\frac{\partial}{c\partial t}E_x -\pdiff{y}B_z -\pdiff{z}(-B_y) =\frac{4\pi}{c}j_{1}=\frac{4\pi}{c}(-j_x),\\ &\rightarrow\quad \ppdiff{B_z}{y}-\ppdiff{B_y}{z}=\frac{1}{c}\ppdiff{\mb{E}}{t}+\frac{4\pi}{c}j_x \quad \mathrm{or}\quad \bigl(\nabla\times\mb{B}\bigr)_{x}=\frac{1}{c}\ppdiff{E_x}{t}+\frac{4\pi}{c}j_{x},\\ &\partial^{\,\mu}F_{\mu 0}=\partial^{\,0}F_{00}+\partial^{\,1}F_{10}+\partial^{\,2}F_{20}+\partial^{\,3}F_{30} =-\pdiff{x}(-E_x)-\pdiff{y}(-E_y)-\pdiff{z}(-z)=\frac{4\pi}{c}c\rho, \\ &\rightarrow\quad \ppdiff{E_x}{x}+\ppdiff{E_y}{y}+\ppdiff{E_z}{z}=\nabla\cdot\mb{E}=4\pi\rho \end{align*} |
| ↑7 | これは \(A\) を完全に定義するには十分ではない．依然として \(\square^{2}\chi=0\) を満たすどんな \(\chi\) も用いることが出来る． |
