\(\)
Problem 9-1
Show that \(\def\mb#1{\mathbf{#1}}\mb{E},\,\mb{B}\), and \(\mb{k}\) are muturally perpendicular for this plane-wave solution \(\mb{A}(\mb{r},t)=\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}\).
解答する前に, この問題に関連した本文の式 (9-12) について言及しておく．原典では, 式 (9-12) について次のように述べている： If we expand \(\mb{A}\) in running plane waves, that is,
\begin{equation}
\mb{A}(\mb{R},t) = \mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{R}}
\tag{9-12}
\end{equation}
\mb{A}(\mb{R},t) = \mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{R}}
\tag{9-12}
\end{equation}
しかし, ここは校訂版のように修正するべきであろう： If we assume \(\mb{A}\) is a running plane wave, that is, \(\dotsb\)
校訂版の訳本では, この部分が原典のまま訳されているので注意しよう．
( 解答 ) ここの解答は, 砂川：「理論電磁気学」の § 8-2 の記述を, この本に合わせたものである．
本文で前述された式： \(\ddot{\mb{a}}_{\mb{k}}(t)=-c^{2}k^{2}\,\mb{a}_{\mb{k}}(t)\) から \(\mb{a}_{\mb{k}}(t)\) は, \(\omega=ck\) として次とすることが出来る：
\begin{equation}
\mb{a}_{\mb{k}}(t)=\mb{e}^{(1)}a_k\,e^{-i\omega t}
\tag{1}
\end{equation}
\mb{a}_{\mb{k}}(t)=\mb{e}^{(1)}a_k\,e^{-i\omega t}
\tag{1}
\end{equation}
ただし \(\mb{e}^{(1)}\) は, 波動の偏りの方向を示す単位ベクトルである．この結果と式 (9-12)： \(\mb{A}(\mb{r},t)=\mb{a}_{\mb{k}}(t)e^{i\mb{k}\cdot\mb{r}}\), そして \(\mb{e}^{(3)}\) を波数ベクトル \(\mb{k}\) の方向(すなわち波動の進行方向)の単位ベクトルとすると, ベクトルポテンシャルは次に書ける：
\begin{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\mb{A}(\mb{r},t)=\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}=\mb{e}^{(1)}\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)},\quad\text{where}\quad
\omega=c|\mb{k}|,\quad \mb{k}=\mb{e}^{(3)}k
\tag{2}
\end{equation}
\def\pdiff#1{\frac{\partial}{\partial #1}}
\def\reverse#1{\frac{1}{#1}}
\def\Bppdiff#1#2{\frac{\partial^{2} #1}{\partial #2^{2}}}
\def\ppdiff#1#2{\frac{\partial #1}{\partial #2}}
\mb{A}(\mb{r},t)=\mb{a}_{\mb{k}}(t)\,e^{i\mb{k}\cdot\mb{r}}=\mb{e}^{(1)}\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)},\quad\text{where}\quad
\omega=c|\mb{k}|,\quad \mb{k}=\mb{e}^{(3)}k
\tag{2}
\end{equation}
これは波動方程式の1つの解で \(\mb{k}\) の方向に進行する平面波を表している [1]【 参考 】 単色平面波について, ランダウ：「力学・場の理論」の§ 70 の一部を抜粋し, 以下に示しておこう． § 70. … Continue reading． \(a_k=|\mb{a}_{\mb{k}}|\) は波動の振幅であり， \(\omega\) は角振動数である．式 (9-13)： \(\mb{k}\cdot\mb{a}_{\mb{k}}=0\) から, この波動 \(\mb{A}\) の偏りの方向 \(\mb{e}^{(1)}\) は, 波動の進行方向 \(\mb{k}\) に直角になっていなくてはならない．
式 (2) を, 式 (9-8)：\(\nabla\cdot\mb{A}=0\) に代入すると,
\begin{equation}
\mathrm{div}\,\mb{A}(\mb{r},t)=\pdiff{\mb{r}}\cdot\mb{A}(\mb{r},t)=\mb{e}^{(1)}\cdot(i\mb{k})\,a_{\mb{k}}\,
e^{i(\mb{k}\cdot\mb{r}-\omega t)}=i\mb{e}^{(1)}\cdot\mb{k}\,a_{\mb{k}}\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}=0
\tag{3}
\end{equation}
\mathrm{div}\,\mb{A}(\mb{r},t)=\pdiff{\mb{r}}\cdot\mb{A}(\mb{r},t)=\mb{e}^{(1)}\cdot(i\mb{k})\,a_{\mb{k}}\,
e^{i(\mb{k}\cdot\mb{r}-\omega t)}=i\mb{e}^{(1)}\cdot\mb{k}\,a_{\mb{k}}\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}=0
\tag{3}
\end{equation}
これが任意の \(\mb{r},t\) に於いて成立するためには, 波動の進行方向 \(\mb{k}\) の単位ベクトルを \(\mb{e}^{(3)}\) とするならば,
\begin{equation}
\mb{e}^{(1)}\cdot\mb{k}=k\,\mb{e}^{(1)}\cdot\mb{e}^{(3)}=0\quad\rightarrow\quad
\mb{e}^{(1)}\cdot\mb{e}^{(3)}=0
\tag{4}
\end{equation}
\mb{e}^{(1)}\cdot\mb{k}=k\,\mb{e}^{(1)}\cdot\mb{e}^{(3)}=0\quad\rightarrow\quad
\mb{e}^{(1)}\cdot\mb{e}^{(3)}=0
\tag{4}
\end{equation}
すなわち, 波動の偏り \(\mb{e}^{(1)}\) は波動の進行方向 \(\mb{e}^{(3)}\) に直角になっていなくてはならない．
さらに, 式 (3) を時間微分すると, 式 (9-11) を用いて次となる：
\begin{align}
&\mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t},\quad \nabla^{2}\mb{A}-\frac{1}{c^{2}}\Bppdiff{\mb{A}}{t}=0,\tag{9-11}\\
\rightarrow\quad &\pdiff{t}\mathrm{div}\,\mb{A}(\mb{r},t)=\pdiff{t}\nabla\cdot\mb{A}
=\nabla\cdot\left(\ppdiff{\mb{A}}{t}\right)
=-c\,\nabla\cdot\left(-\reverse{c}\ppdiff{\mb{A}}{t}\right)=-c\nabla\cdot\mb{E}=0
\tag{5}
\end{align}
&\mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t},\quad \nabla^{2}\mb{A}-\frac{1}{c^{2}}\Bppdiff{\mb{A}}{t}=0,\tag{9-11}\\
\rightarrow\quad &\pdiff{t}\mathrm{div}\,\mb{A}(\mb{r},t)=\pdiff{t}\nabla\cdot\mb{A}
=\nabla\cdot\left(\ppdiff{\mb{A}}{t}\right)
=-c\,\nabla\cdot\left(-\reverse{c}\ppdiff{\mb{A}}{t}\right)=-c\nabla\cdot\mb{E}=0
\tag{5}
\end{align}
すなわち \(\mathrm{div}\,\mb{E}=0\) となり, \(\mb{A}\) についての式 (2) と全く同じ議論から, 電場 \(\mb{E}\) もやはり波動の進行方向 \(\mb{e}^{(3)}\) に直角な成分だけを持つことになる．その電場 \(\mb{E}\) は, 式 (9-11) に式 (2) を代入して得られ, 電場 \(\mb{E}\) の偏りは \(\mb{e}^{(1)}\) 方向であることが分かる：
\begin{equation}
\mb{E}(\mb{x},t)=-\reverse{c}\ppdiff{\mb{A}}{t}
=-\reverse{c}\pdiff{t}\mb{e}^{(1)}\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
=\mb{e}^{(1)}\,\frac{i\omega}{c}\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
\tag{6}
\end{equation}
\mb{E}(\mb{x},t)=-\reverse{c}\ppdiff{\mb{A}}{t}
=-\reverse{c}\pdiff{t}\mb{e}^{(1)}\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
=\mb{e}^{(1)}\,\frac{i\omega}{c}\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
\tag{6}
\end{equation}
次に磁場も式 (9-7)：\(\mb{B}=\nabla\times\mb{A}\) から求まる．例えば \(x\) -成分を示すと,
\begin{align}
\mb{B}(\mb{x},t)_x&=\left(\mathrm{rot}\,\mb{A}\right)_x=\ppdiff{A_z}{y}-\ppdiff{A_y}{z}
=\pdiff{y}\left\{e_z^{(1)}a_ke^{i(\mb{k}\cdot\mb{r}-\omega t)}\right\}
-\pdiff{z}\left\{e_y^{(1)}a_ke^{i(\mb{k}\cdot\mb{r}-\omega t)}\right\}\notag\\
&=i(k_ye_k^{(1)}-k_ze_y^{(1)})_x\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
=(\mb{k}\times\mb{e^{(1)}})_x\,ia_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
\tag{7}
\end{align}
\mb{B}(\mb{x},t)_x&=\left(\mathrm{rot}\,\mb{A}\right)_x=\ppdiff{A_z}{y}-\ppdiff{A_y}{z}
=\pdiff{y}\left\{e_z^{(1)}a_ke^{i(\mb{k}\cdot\mb{r}-\omega t)}\right\}
-\pdiff{z}\left\{e_y^{(1)}a_ke^{i(\mb{k}\cdot\mb{r}-\omega t)}\right\}\notag\\
&=i(k_ye_k^{(1)}-k_ze_y^{(1)})_x\,a_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
=(\mb{k}\times\mb{e^{(1)}})_x\,ia_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
\tag{7}
\end{align}
となり, 他の成分も同様である．従って, 磁場は次で与えられることが分かる：
\begin{align}
&\mb{B}(\mb{x},t)=(\mb{k}\times\mb{e}^{(1)})\,ia_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
=\mb{e}^{(2)}\,ika_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)},
\tag{7}\\
&\quad \text{where}\quad\mb{e}^{(2)}=\frac{\mb{k}}{k}\times\mb{e}^{(1)}=\mb{e}^{(3)}\times\mb{e}^{(1)}
\tag{9}
\end{align}
&\mb{B}(\mb{x},t)=(\mb{k}\times\mb{e}^{(1)})\,ia_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}
=\mb{e}^{(2)}\,ika_k\,e^{i(\mb{k}\cdot\mb{r}-\omega t)},
\tag{7}\\
&\quad \text{where}\quad\mb{e}^{(2)}=\frac{\mb{k}}{k}\times\mb{e}^{(1)}=\mb{e}^{(3)}\times\mb{e}^{(1)}
\tag{9}
\end{align}
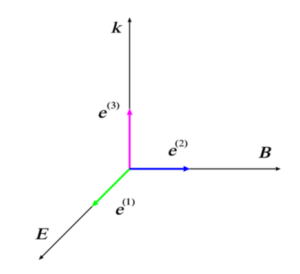
このとき磁場の方向を表わす単位ベクトル \(\mb{e}^{(2)}\) は, 電場の方向ベクトル \(\mb{e}^{(1)}\) と進行方向の単位ベクトル \(\mb{e}^{(3)}\) の両方に直交する単位ベクトルである．
以上から, 電波 \(\mb{E}\) と磁波 \(\mb{B}\) は進行方向 \(\mb{k}\) に直角な偏りを持ち, かつそれらはまた互いに直交していることが分かる(下図を参照すべし)．
図 1. 平面電磁波の偏りと偏極ベクトル \(\mb{e}^{(i)}\)．
References
| ↑1 | 【 参考 】 単色平面波について, ランダウ：「力学・場の理論」の§ 70 の一部を抜粋し, 以下に示しておこう．
§ 70. 単色平面波電磁波の特別な場合として非常に重要なのは, 場が時間の単一周期の関数であるような波である．このような波は「単色」と呼ばれる．単色波に於けるあらゆる量(ポテンシャル, 場の成分)は, \(\cos(\omega t+\alpha)\) という形の因子を通じて時間に関係する．量 \(\omega\) は波の「角振動数」と呼ばれる．(\(x\)-軸に沿って伝播する)平面波では, 場は \(t-x/c\) だけの関数である．従って, もし平面波が単色であれば, その場は \(t-x/c\) の単一周期の関数である．このような波のベクトルポテンシャルは, 複素数の表式の実数部分として書くことが最も便利である： \begin{equation} \mb{A}=\mathrm{Re}\,\big\{\mb{A}_{0}\,e^{-i\omega (t-x/c)}\big\} \tag{70.1} \end{equation} ここで \(\mb{A}_0\) は, ある定数の複素ベクトルである．明らかにこのような波の場 \(\mb{E}\) 及び \(\mb{H}\) は, 同じ振動数 \(\omega\) の同様な形を持ち, 次に書ける： \begin{equation} \def\ppdiff#1#2{\frac{\partial #1}{\partial #2}} \mb{E}=-\frac{1}{c}\ppdiff{\mb{A}}{t}=-\frac{1}{c}\mb{A}’,\quad \mb{H}=\nabla\times\mb{A}=\nabla\left(t-\frac{x}{c}\right)\times\mb{A}’=-\frac{1}{c}\mb{n}\times\mb{A}’ \tag{69.3} \end{equation} ただし, ダッシュは \(t-x/c\) についての微分を表わし, \(\mb{n}\) は波の伝播方向の単位ベクトルである．第１の式を第２の式に代入して次式が得られる： \begin{equation} \mb{H}=\mb{n}\times\mb{E} \tag{69.4} \end{equation} 次の量 \begin{equation} \lambda=\frac{2\pi c}{\omega} \tag{70.2} \end{equation} は「波長」と呼ばれる：それは固定した時刻 \(t\) に於ける座標 \(x\) についての場の変化の周期である．次のベクトル \begin{equation} \mb{k}=\frac{\omega}{c}\mb{n} \tag{70.3} \end{equation} は,「波数ベクトル」と呼ばれる(ただし \(\mb{n}\) は波の伝播方向の単位ベクトル)．これを使うと, 式 (70.1) を座標軸の選び方に依らない形 \begin{equation} \mb{A}=\mathrm{Re}\,\big\{\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}\big\} \tag{70.4} \end{equation} に書くことが出来る．指数に於ける \(i\) のかかった量は,「波の位相」と呼ばれる．線形の演算だけをこれらの量に対して行なう限りでは, 実数部分をとるという記号を落として, 複素数の量自体について演算を行なうことが出来る．そうすると \(\mb{A}=\mb{A}_0\,e^{i(\mb{k}\cdot\mb{r}-\omega t)}\) を式 (69.3) に代入して, 平面単色波の場の強さとベクトルポテンシャルとの間の関係を, \begin{equation} \mb{E}=ik\mb{A},\quad \mb{H}=i\mb{k}\times\mb{A} \tag{70.5} \end{equation} という形に求められる． |
|---|
