\(\)
問題 6-23 の解答例を書く際に, ボーム:「量子論」の第21章 §18 を参照したのだが, そこを理解するために前の部分も読んでいたら「平均自由行路」(mean free path) を得るやり方が書かれており, 初等的な導出法とは異なるやり方で面白いと感じた. そこで, 問題の回答には直接関係ないけれど紹介しておこうと思う. (ウィキペディアのEnglish版では似た導出の説明がなされているようである).
初等的な導出法
まずは初等的な導出法は, 例えば, 戸田:「分子運動30講」からの抜粋で紹介するならば次となる (文字や表現を多少は変えている).
気体の分子の速さは秒速数百mに達するが, 例えばアンモニアの蒸気の匂いが拡がって来るのには, いくらかの時間が掛かる. これは気体の分子が大きさを持つために絶えず他の分子と衝突して進行方向を変えジグザクな運動をするためである. ある分子が衝突してから次に衝突するまでに走る距離は勿論一定ではないが, その平均を考えてこれを気体分子の「平均自由行路」という. 〜 略す 〜.
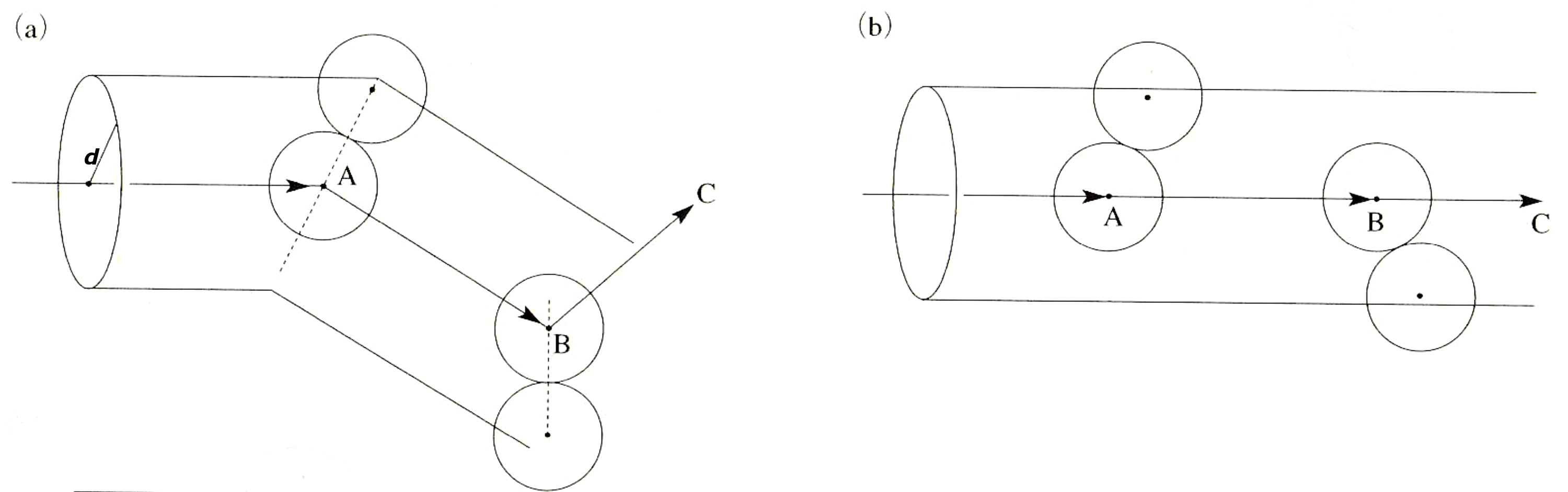
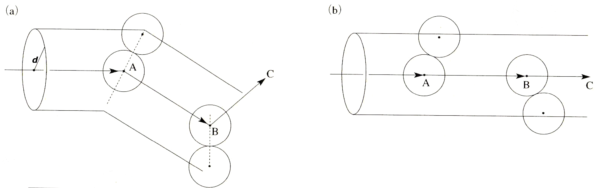
平均自由行路を近似的に求めるには, 他の分子は全て静止しているとして, これらの一つの分子が衝突する運動を考えればよい. この分子は, 相次ぐ衝突の間は直進し, ジグザグではあるがだいたい速さ \(v\) で動く. 下図1. の図 (a) はこの様子を示す. このジグザグの経路を真っ直ぐに伸ばしたと考えたのが図 (b) の方である.
2分子間の距離を \(d=2a\) とすると, 行路の中心線を中心とする半径 \(d\) の円筒形に他の分子が在れば衝突が起こる. 単位体積内の分子数を \(\rho\) とすると図 (b) から分かるように, 1秒間の衝突数はこの円筒内の分子数 \(N=\rho\pi d^{2}v\) に等しい. \(v\) は分子が1秒間に走る距離であるから, 相次ぐ衝突間の距離 \(l\) は
(衝突間の距離) \times (1秒間の衝突数) = v \quad\rightarrow\quad
l\times N= l\times \rho\pi d^{2}v =v
\tag{1}
\end{equation}
よって,
l=\frac{1}{\rho\pi d^{2}}=\frac{1}{\rho\,\sigma}
\tag{2}
\end{equation}
ただし, \(\sigma = \pi d^{2}\) は「分子が進む方向から見た場合にその中で衝突が起こり得る領域の断面積になっているので「散乱断面積」と呼ばれる. この式 (2) の \(l\) が「平均自由行路」の近似式である. 式から「分子密度 \(\rho\) が大きいほど, また分子の直径 \(d\) が大きいほど, 自由行路 \(l\) は小さくなる」ことが分かる.
ボームの導出法
次に確率論の定理を利用したボームの方法を示す.
物質のある与えられた厚さ \(dx\) を通過する際に, 粒子が散乱される確率は「散乱断面積」と呼ばれる量で表わすことが出来る. 物質中の各分子は, 入射粒子に対して面積 \(\sigma=\pi d^{2}\) の標的になっていると考えることが出来る. 標的が十分に薄くて多重散乱を無視できる場合を考えることにする.
分子密度を \(\rho\) とすると面積 \(A\) で暑さ \(dx\) の標的物質片の中には \(\rho A dx\) 個の分子が入っているから, 標的の総面積は \(\sigma\rho A\,dx\) に等しく, これが有効断面積を与えることになる. その際に, 分子によって占められている部分の割合は \(\sigma\rho A\,dx/A=\sigma\rho\,dx\) である. 入射粒子が衝突を起こす確率 \(dP\) はちょうどこの部分の割合に等しい. よって,
dP = \rho\,\sigma\,dx
\tag{3}
\end{equation}
ただし, 上述のように考えた場合には分子が半径 \(a\) の球形であるならば, 二個の分子の中心間の距離が \(d=2a\) だから \(\sigma=\pi d^{2}\) に相当している.
平均自由行路を得るために, まずは「粒子が距離 \(x\) の間に衝突を起こさない確率 \(Q(x)\)」を計算する. これは「自由行路が \(x\) 若しくはそれ以上である確率」を与える. これを求めるために, 距離 \(x+dx\) での確率 \(Q(x+dx)\) を考える. それは「距離 \(x\) の間に衝突を起こさない確率」と「次の距離 \(dx\) でも衝突を起こさない確率」を掛け合わせたものと考えることが出来ることに注目する. 区間 \([x,\,x+dx]\) の間に衝突を起こす確率を上式 (3) の \(dP\) とすれば, 「距離 \(dx\) の間に衝突を起こさないこと」は「衝突を起こすこと」の「余事象」であるから, その確率は \(1-dP\) である. よって,
Q(x+dx)= Q(x)\times\big(1-dP\big)
\tag{4}
\end{equation}
これが \(Q(x+dx)\) の一次近似式に一致するとすれば,
Q(x+dx) = Q(x) + \frac{d Q(x)}{dx}dx = Q(x)\times\big(1-dP\big)= Q(x) – Q(x)\,dP
\tag{5}
\end{equation}
従って,
dQ(x)=\frac{d Q(x)}{dx}dx = -Q(x)dP = -Q(x)\,\rho\,\sigma\,dx \quad \rightarrow\quad
\frac{dQ}{Q}=-\rho\,\sigma\,dx
\tag{6}
\end{equation}
この微分方程式を, 初期条件 \(Q(0)=1\) の下で解くと次を得る:
Q(x)=e^{-\rho\sigma x}
\tag{7}
\end{equation}
自由行路が区間 \([x,\,x+dx]\) に在る確率は \(dQ\) であるから,それは次のように表せる:
dQ(x) = \left| \frac{dQ(x)}{dx}\right|\,dx =\left|\frac{d}{dx}\big( e^{-\rho\sigma x}\big)\right|\, dx
=\big|-\rho\,\sigma\, e^{-\rho\sigma x} \big|\,dx = \rho\,\sigma\,e^{-\rho\sigma x}\,dx
\tag{8}
\end{equation}
そして,「平均自由行路 \(l\) は行路長 \(x\) の期待値であると見做す」ならば,
l=\int_{0}^{\infty} x\,dQ(x)= \int_{0}^{\infty} x\,\left| \frac{dQ(x)}{dx}\right|\,dx =\rho\,\sigma
\int_{0}^{\infty} x\,e^{-\rho\sigma x}\,dx =\frac{1}{\rho\sigma}
\tag{9}
\end{equation}
となり, 上記の式 (2) と同じ結果が得られる. ただし, 次の部分積分を用いている:
I=\int_{0}^{\infty} x\,e^{-a x}\,dx = \left[ \frac{e^{-ax}}{-a}\right]_{0}^{\infty} -\int_{0}^{\infty} \frac{e^{-a x}}{-a}\,dx =\frac{1}{a}\int_{0}^{\infty} e^{-a x}\,dx = \frac{1}{a^{2}}
\tag{10}
\end{equation}