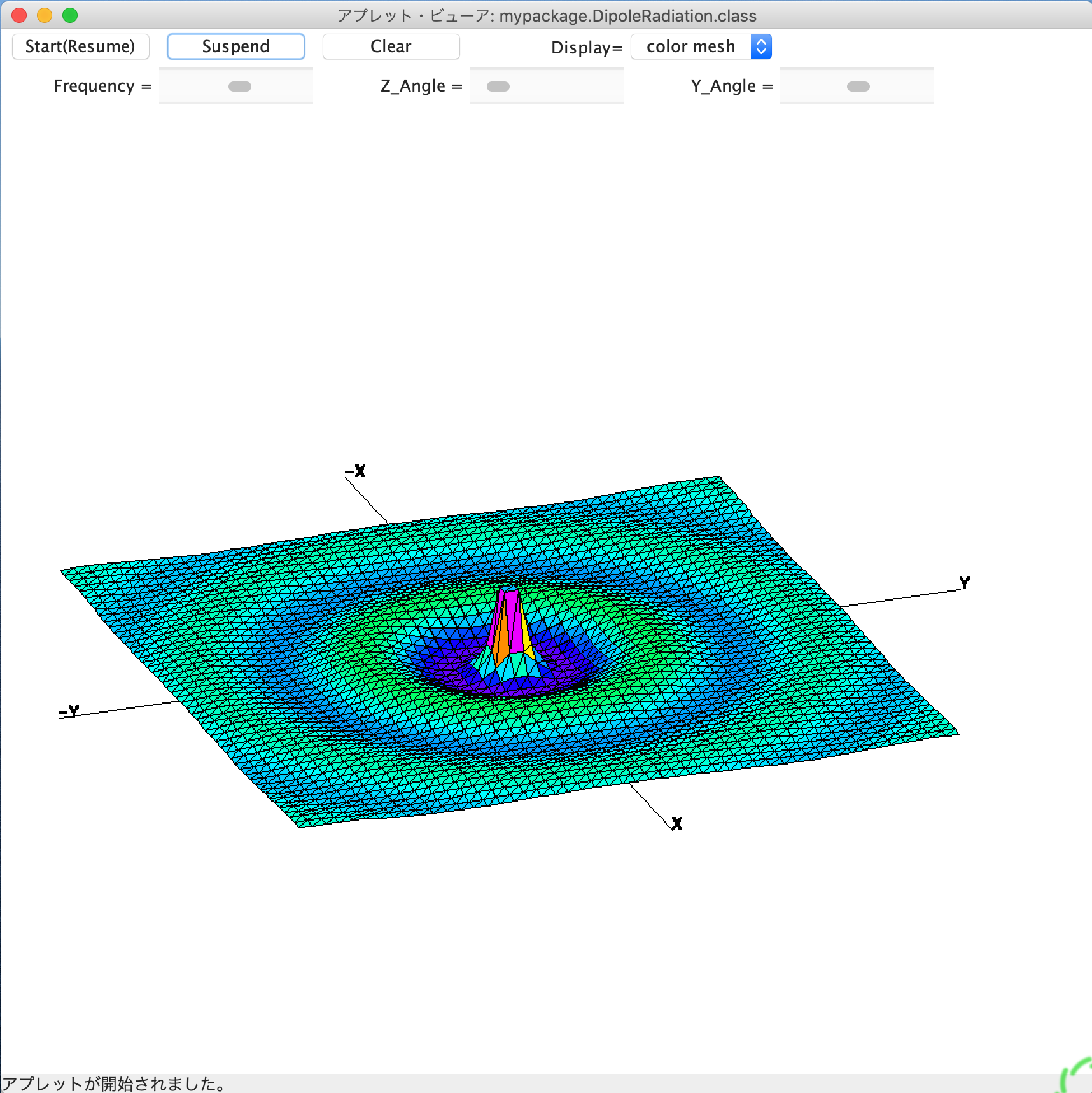
\(\)
前のブログ中で双極放射について言及した． 実は約9年くらい前ではあるが, Java による「双極放射のシュミレーション」を行うアニメーションプログラムを書いた． 「シミュレーション」と言えるような厳密なものではないが, 一応は双極放射の振舞いを視覚的に知ることは出来るのではないかと思う． 明らかに初期画面の設定部分にバグが存在するし, 正当でない部分があるとは思うが, 自分のパソコン環境では一応はそれらしく動くように見える． そこで取り敢えずは, そのソースプログラムを提示しておこう． もしバグの修正が出来たならば, プログラム更新しようと思う．
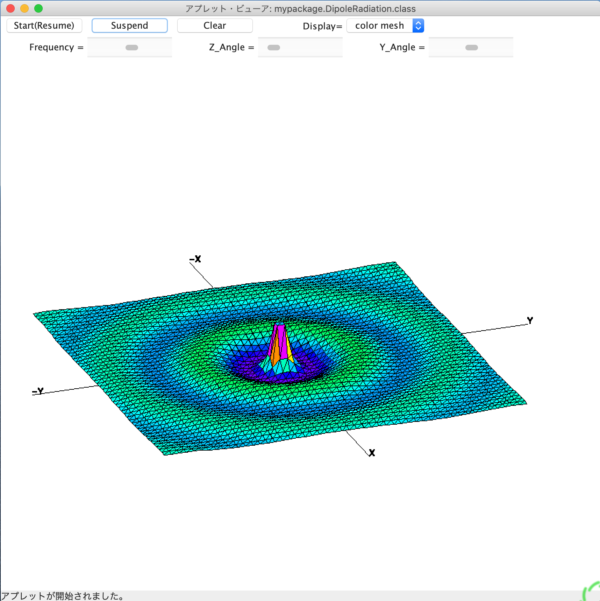
【 追伸 】 初期画面の不具合を修正したものに付け替えました．この修正版では,「半波長だけ離して複数の双極子を並べると放射場に指向性が生じる」ことをシュミレーション出来るような補強もしました (ただし双極子が4本の場合は実行結果の様子のみを示す)．不具合の修正は初期画面以外にも色々行ったので, ソースプログラムは２つとも全部入れ替えました．なので, もし自分のPC上でコンパイルしてプログラム実行する際には, もう一度示された手順をやり直して下さい．
図 1. DipoleRadiation.java を実行しているときのパソコン画面．
まずは, プログラムを書く際に必要となる数式を求めておこう． ブログ記事「電磁波の放射について」中の「双極放射」での式 (20) は次であった：
\begin{equation}
\def\mb#1{\mathbf{#1}}
\mb{E}=\frac{1}{c^{2}R_{0}}\big(\ddot{\mb{d}}\times\mb{n}\big)\times\mb{n}
\tag{1}
\end{equation}
\def\mb#1{\mathbf{#1}}
\mb{E}=\frac{1}{c^{2}R_{0}}\big(\ddot{\mb{d}}\times\mb{n}\big)\times\mb{n}
\tag{1}
\end{equation}
ここで, 電荷 \(e\) が \(z\) 軸方向で振動数 \(\omega_{0}\) の「周期運動」をするならば, 「双極モーメント」 \(\mb{d}=e\mb{r}=e\mb{k}r\equiv \mb{k}d\) も, 次のような調和振動を行う：
\begin{equation}
\mb{r}=\mb{k}r\,\sin\omega_{0}t,\quad\rightarrow\quad
\mb{d}=e\mb{k}r\,\sin\omega_{0}t=\mb{k}d\,\sin\omega_{0}t
\tag{2}
\end{equation}
\mb{r}=\mb{k}r\,\sin\omega_{0}t,\quad\rightarrow\quad
\mb{d}=e\mb{k}r\,\sin\omega_{0}t=\mb{k}d\,\sin\omega_{0}t
\tag{2}
\end{equation}
ただし \(\mb{k}\) は \(z\) 方向の単位ベクトルとする． このとき,
\begin{equation}
\dot{\mb{d}}=\mb{k}d\,\omega_{0}\cos\omega_{0}t,\quad
\ddot{\mb{d}}=-\mb{k}d\,\omega^{2}_{0}\sin\omega_{0}t
\tag{3}
\end{equation}
\dot{\mb{d}}=\mb{k}d\,\omega_{0}\cos\omega_{0}t,\quad
\ddot{\mb{d}}=-\mb{k}d\,\omega^{2}_{0}\sin\omega_{0}t
\tag{3}
\end{equation}
この双極モーメントが原点 O にあるとき, そこから \(R_{0}\) だけ離れた「\(x\)-\(y\) 平面」上の地点 \(\mb{R}_{0}=\mb{n}R_{0}\) では, やはり \(z\) 軸方向に振動電場が生起する ( 図 2 を参照 )． ただし, この場合のベクトル \(\mb{n}\) は観測地点 \(\mb{R}_{0}\) の方向を向いた単位ベクトルとなる． また, このときの電場はすべて「時間が \(t’=t-R_{0}/c\) に於けるものである」ことに注意する！．以上から, その位置に生起する電場の大きさは, 式 (1) と式 (3) より次となる：
\begin{align}
\mb{E}&=\frac{1}{c^{2}R_{0}}\big(-\mb{k}d\,\omega^{2}_{0}\sin\omega_{0}t’\,\times\mb{n}\big)\times\mb{n}\,\bigg|_{t’=t-R_{0}/c}
=-\frac{d\,\omega^{2}_{0}\,\sin\omega_{0}(t-R_{0}/c)}{c^{2}R_{0}}\,\big(\mb{k}\times\mb{n}\big)\times\mb{n}\notag\\
&=\mb{d}\,\frac{\,k_{0}^{2}}{R_{0}}\sin\,(\omega_{0}t-k_{0}R_{0})
\tag{4}
\end{align}
\mb{E}&=\frac{1}{c^{2}R_{0}}\big(-\mb{k}d\,\omega^{2}_{0}\sin\omega_{0}t’\,\times\mb{n}\big)\times\mb{n}\,\bigg|_{t’=t-R_{0}/c}
=-\frac{d\,\omega^{2}_{0}\,\sin\omega_{0}(t-R_{0}/c)}{c^{2}R_{0}}\,\big(\mb{k}\times\mb{n}\big)\times\mb{n}\notag\\
&=\mb{d}\,\frac{\,k_{0}^{2}}{R_{0}}\sin\,(\omega_{0}t-k_{0}R_{0})
\tag{4}
\end{align}
ただし, \(k_{0}=2\pi/\lambda_{0}=\omega_{0}/c\) は「波数」である． これより, 生起する電場 \(\mb{E}\) の振動方向は, やはり双極子 \(\mb{d}\) と同じ振動方向, すなわち \(z\) 方向であることが分かる．
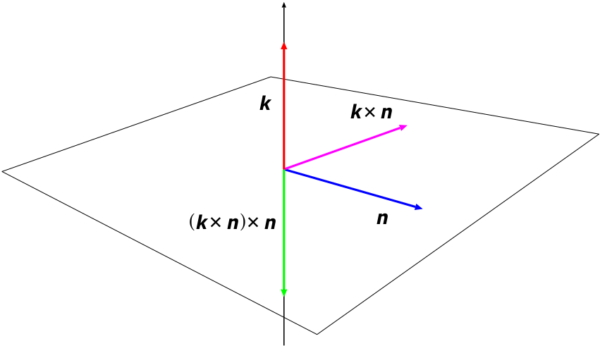
図 2. 双極モーメントの振動方向が \(z\) 軸方向であると, \((\mb{k}\times\mb{n})\times\mb{n}\) は 負の \(z\) 方向の単位ベクトル \(-\mb{k}\) になることが分かる．
参考までに, もし観測地点 \(\mb{R}_{0}\) が \(x\)-\(y\) 平面上でなくて, 3次元空間のある一般的な方向にある場合ではどうなるかについて述べておこう． この場合の方向ベクトル \(\mb{n}\) の成分は, 3次元極座標表示から次である：
\begin{equation}
\mb{n}=\big(\sin\theta\cos\phi,\, \sin\theta\sin\phi,\, \cos\theta\big)
\tag{5}
\end{equation}
\mb{n}=\big(\sin\theta\cos\phi,\, \sin\theta\sin\phi,\, \cos\theta\big)
\tag{5}
\end{equation}
従って, 方向ベクトル \(\mb{k}=(0,0,1)\) との外積は次のようになる：
\begin{align}
&\mb{k}\times\mb{n}=\big(-\sin\theta\sin\phi,\, \sin\theta\cos\phi,\,0\big),\notag\\
&(\mb{k}\times\mb{n})\times\mb{n}=\big(\sin\theta\cos\theta\cos\phi,\, \sin\theta\cos\theta\sin\phi,\, -\sin^{2}\theta\big),\notag\\
\rightarrow&\quad \big|(\mb{k}\times\mb{n})\times\mb{n}\big|
=\sin\theta\,\big|\big(\cos\theta\cos\phi,\,\cos\theta\sin\phi,\,-\sin\theta\big)\big|=\sin\theta
\tag{6}
\end{align}
&\mb{k}\times\mb{n}=\big(-\sin\theta\sin\phi,\, \sin\theta\cos\phi,\,0\big),\notag\\
&(\mb{k}\times\mb{n})\times\mb{n}=\big(\sin\theta\cos\theta\cos\phi,\, \sin\theta\cos\theta\sin\phi,\, -\sin^{2}\theta\big),\notag\\
\rightarrow&\quad \big|(\mb{k}\times\mb{n})\times\mb{n}\big|
=\sin\theta\,\big|\big(\cos\theta\cos\phi,\,\cos\theta\sin\phi,\,-\sin\theta\big)\big|=\sin\theta
\tag{6}
\end{align}
従って, このような 3 次元空間の一般的な方向では, 観測地点 \(\mb{R}_{0}\) の方向ベクトル \(\mb{n}\) と \(z\)-軸とのなす角度を \(\theta\) とすれば,「電場の方向は \(\mb{e}_{\theta}\) 方向で, 大きさは式 (4) に \(\sin\theta\) だけ余分な因子が付加する」ことになる．
\begin{equation}
\mb{E}_{\theta}=d\,\mb{e}_{\theta}\,\sin\theta\,\frac{\,k_{0}^{2}}{R_{0}}\,\sin\,(\omega_{0}t-k_{0}R_{0})
\tag{7}
\end{equation}
\mb{E}_{\theta}=d\,\mb{e}_{\theta}\,\sin\theta\,\frac{\,k_{0}^{2}}{R_{0}}\,\sin\,(\omega_{0}t-k_{0}R_{0})
\tag{7}
\end{equation}
よって, 観測地点が \(z\)-軸に近づくに連れて, 放射の大きさは小さくなって行く．(図 3 を参照のこと)．
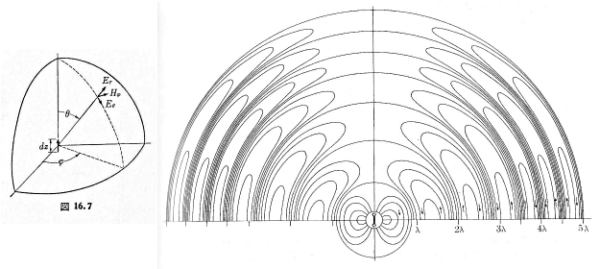
図 3. 観測方向への電気双極子放射では, 電場は図の \(E_{\theta}\) 方向のみでその大きさには因子 \(\sin\theta\) が付加する． 右図は振動する双極子によって生成される電場の様子である．(末松,Panofsky&Phillipsより)
以下は, 峯村吉泰 著「Javaによるコンピュータグラフィックス」(森北出版) に書かれていた Java プログラムを全面的に参照し, それに多少の修正をして, 上記の式 (4) が表していること, すなわち「原点 O にある双極子が単振動して電場 \(\mb{E}\) を放射するとき, \(x\)-\(y\) 平面上でその電場(の大きさ)はどんな具合に伝搬して行くのか」をアニメーションするようにしたものである． 従って, プログラムを読んで見て分からない部分があったならば, そちらの本を見て欲しい．
Java の実行環境のある方は, 例えば以下の手順で動かして見て頂きたい． ただし, しばらくプログラミングをしていなかったら, 最新の JDK では Java アプレットは廃止されているらしい． なので, 以前の開発実行環境 Java SE 8 や Eclipse 2018 などを用いて作業して頂きたい．
- まずは, 以下に示した ３ つのソースファイル prog.html, DipoleRadiation.java, DrawCanvas.java をコピー&ペーストして同名のファイルを作成する．
- 次に java のコマンド javac で 2つの Java ファイルをコンパイルする：
$ javac DipoleRadiation.java DrawCanvas.javaすると同じディレクトリに java のバイトコードである DipoleRadiation.class と DrawCanvas.class が作られる． - 最後に java のコマンド appletviewer でプログラムの実行を見る：
$ appletviewer prog.html
プログラムの動かし方は, 実行画面のボタンを見ればすぐ分かるであろう． まずは Y-angle を少し動かして傾きを変化させてから Start ボタンを押して開始して欲しい． Display を color mesh にするとカラフルな図形が見えると思う．
(1) 双極子が3本の場合：
(2) 双極子が4本の場合：
prog.html :
<!-- prog.html --> <html> <body> <applet-desc main-class="DipoleRadiation" width="800" height="800"> </body> </html>
DipoleRadiation.java :
// DipoleRadiation.java
/**************************************************************************************
* 双極子放射のシミュレーション
* by ISSHY on September, 23, 2011 , revised on October, 22, 2011.
revised on July, 5, 2020.
<applet code="DipoleRadiation.class" width="800" height="800"></applet>
***************************************************************************************/
import java.applet.Applet;
import java.awt.BorderLayout;
import java.awt.Button;
import java.awt.Choice;
import java.awt.Color;
import java.awt.Graphics;
import java.awt.GridLayout;
import java.awt.Image;
import java.awt.Label;
import java.awt.Panel;
import java.awt.Scrollbar;
import java.awt.TextField;
import java.awt.event.ActionEvent;
import java.awt.event.ActionListener;
import java.awt.event.AdjustmentEvent;
import java.awt.event.AdjustmentListener;
import java.awt.event.ItemEvent;
import java.awt.event.ItemListener;
public class DipoleRadiation extends Applet
implements ActionListener,AdjustmentListener,ItemListener,Runnable{
// 使用するメンバー名
Scrollbar scrK,scrW,scrZ,scrY;
int sliderW,sliderZ,sliderY;
private DrawCanvas drw;
private Thread thread; // スレッドオブジェクトの変数を定義
private Image img;
private Graphics bg;
private Button b_start, b_stop, b_clear;// アニメ開始と停止用ボタン名を定義
private Choice ch_select;
private double PI = Math.PI;
private double x [], y [], z [];
private double xp [], yp [], xm [], ym [];
int n=0,flag=0;
int Width, Height,Nxmin,Nymin;
int Nup=200,Nbot=20; // Nup=50,Nbot=20;
int Stepmax=200000;
int Interval=40;
int t=0,T=10000; // 時間
double dt = 0.0003; // 時間のステップ幅
int N=70,M=N;
private int[][] E = new int [2*N*M][3];
double k; // 波数
double w; // 角周波数
double c=3.0; // 位相速度
double amp=0.005; // 最大振幅
double region=2*PI; // 表示する範囲
double angleZ,angleY; // Z軸、Y軸の回転角度
String str;
boolean error=false;
TextField text0;
Thread animator;
// GUI環境（対話型画面）の設定
public void init(){
setLayout( new BorderLayout());
Panel p= new Panel();
p.setLayout( new GridLayout(2,5,1,1));
b_start = new Button("Start(Resume)"); // RESUMEボタンを定義
b_stop = new Button("Suspend");// SUSPENDボタンを定義
b_clear = new Button("Clear"); // CLEARボタン
p.add(b_start); p.add(b_stop); // ボタンをパネルに取付け
p.add(b_clear);
ch_select = new Choice();
ch_select.addItem("black mesh");
ch_select.addItem("color mesh");
ch_select.addItem("Three Dipole");
ch_select.select("black mesh");
p.add(new Label("Display=",Label.RIGHT)); p.add(ch_select);
str="black mesh";
scrW = new Scrollbar( Scrollbar.HORIZONTAL);
scrZ = new Scrollbar( Scrollbar.HORIZONTAL);
scrY = new Scrollbar( Scrollbar.HORIZONTAL);
scrW.setValues(15, 1, 6, 24); // スライダーの(初期値、幅、最小値、最大値)
scrZ.setValues(20, 1, 0, 90);
scrY.setValues(25, 1, 0, 90);
scrW.setUnitIncrement(1); // 方向ボタンの増分を設定
scrZ.setUnitIncrement(1); scrY.setUnitIncrement(1);
sliderW=15; sliderZ=20; sliderY=25; // 初期値を代入
w=(double)sliderW;
k=w/c;
angleZ=sliderZ*PI/180.0;
angleY=sliderY*PI/180.0; // これが抜けていた！！！！！！！．
// スクロールバーをパネルに取り付け
p.add(new Label( "") ); // 空白のラベルを取り付け
p.add(new Label( "") ); // 空白のラベルを取り付け
p.add(new Label( "Frequency = ", Label.RIGHT )); p.add(scrW);
p.add(new Label( "Z_Angle = ", Label.RIGHT )); p.add(scrZ);
p.add(new Label( "Y_Angle = ", Label.RIGHT )); p.add(scrY);
p.add(new Label( "") ); // 空白のラベルを取り付け
add("North",p); // パネルを上部に取り付け
b_start.addActionListener(this); // イベントリスナー登録
b_stop.addActionListener(this);
b_clear.addActionListener(this);
ch_select.addItemListener(this);
scrW.addAdjustmentListener( this );
scrZ.addAdjustmentListener( this );
scrY.addAdjustmentListener( this );
Width = 800; Height = 800;
//Width= getSize().width;
//Height = getSize().height;
setBackground(Color.white);
img = createImage(Width, Height); // イメージ画面
bg = img.getGraphics(); // 裏画面用グラフィックス
animator = new Thread(this);
// ビューポートの設定と座標変換係数の設定
//orig = new double[] {0.0f, PI}; // 原点の位置 orig[0]=x0, orig[1]=y0
drw = new DrawCanvas( img, bg, Width, Height); // 描画オブジェクト生成
drw.viewPort(Nup, Nbot, false, region); // ビューポート変換
drw.gridNum(N, M, E); // 格子点番号付け
inputData(n);
drw.simPaint(x, y, z, angleZ, angleY,N, M, E,flag);
}
// GUI環境を用いたイベント処理
public void actionPerformed(ActionEvent e){ // イベントの定義
if(e.getSource() == b_start){
if(thread == null) thread = new Thread( this );
thread.start();
}
if(e.getSource() == b_stop)
stop();
if(e.getSource() == b_clear){
thread = null;
drw.deleteImage();
n = 0;
inputData(n);
drw.simPaint(x, y, z, angleZ, angleY,N, M, E,flag);
repaint();
}
}
public void adjustmentValueChanged(AdjustmentEvent ev){
if(ev.getSource() == scrW){
sliderW = scrW.getValue();
w=sliderW/1.0;
k=w/c;
System.out.println("w="+w);
}else if(ev.getSource() == scrZ){
sliderZ = scrZ.getValue();
angleZ=sliderZ*PI/180.0;
System.out.println("angleZ="+sliderZ);
}else if(ev.getSource() == scrY){
sliderY = scrY.getValue();
angleY=sliderY*PI/180.0;
System.out.println("angleY="+sliderY);
}
n=0;
inputData(n);
drw.deleteImage();
drw.simPaint(x, y, z,angleZ,angleY,N, M, E,flag);
repaint();
}
public void itemStateChanged(ItemEvent ev){
if(ev.getSource()==ch_select){
str=ch_select.getSelectedItem();
if(str=="black mesh") flag=0;
else if(str=="color mesh") flag=1;
else flag=2;
}
n=0;
inputData(n);
drw.deleteImage();
drw.simPaint(x, y, z, angleZ, angleY,N, M, E,flag);
repaint();
}
// スレッドを実行する命令を記述
public void run(){
while( thread != null ){
n++;
inputData(n);
if(n%Interval==0){
drw.simPaint(x, y, z, angleZ, angleY,N, M, E,flag);
repaint();
try{
thread.sleep( 10 );
} catch(InterruptedException e){ } // 例外処理
}
if(n>Stepmax) stop();
}
}
public void stop(){ thread = null; }
public void update( Graphics g ){
paint( g ); // 画面をクリアしないで paint を呼び出す
}
// メインルーチン
public void paint( Graphics g ){
paintBG();
g.drawImage( img, 0, 0, this );// 裏画面を表画面に
}
public void paintBG(){
bg.clearRect(0, 0, Width, Height);
inputData(n);
drw.simPaint(x, y, z, angleZ, angleY,N, M, E,flag);
}
// 双極子場のデータ入力 ============================
public void inputData(int n){
int s = 0, smax=100000;
x = new double [smax]; y = new double [smax]; z = new double [smax];
xp = new double [smax]; yp = new double [smax];
xm = new double [smax]; ym = new double [smax];
double delta = 2*region/(double)( N - 1 );
double r1=0.0,r2=0.0, r3=0.0;
for( int i = 0; i < N; i++ ){
for( int j = 0; j < M; j++ ){
x[s] = -region + delta * (double)i; y[s] = -region + delta * (double)j;
xp[s] = -region -PI/k+ delta * (double)i; // x-方向へプラス半波長 (λ/2 = π/k) だけ位置がずれている双極子
xm[s] = -region +PI/k+ delta * (double)i; // x-方向へマイナス半波長 (-λ/2 = π/k) だけ位置がずれている双極子
r1 = x[s]*x[s] + y[s]*y[s]; r2 = xp[s]*xp[s] + y[s]*y[s]; r3 = xm[s]*xm[s] + y[s]*y[s];
r1 = Math.sqrt(r1); r2 = Math.sqrt(r2); r3 = Math.sqrt(r3);
if(flag==0 || flag==1) {
if(w*n*dt<=k*r1) z[s]=0;
else z[s]=amp*k*k*(double)Math.sin(w*n*dt-k*r1)/r1;
} else {
if(w*n*dt<=k*r1 && w*n*dt<=k*r2 && w*n*dt<=k*r3) z[s]=0; else
z[s]=amp*k*k*Math.sin(w*n*dt-k*r1)/r1+amp*k*k*Math.sin(w*n*dt-k*r2)/r2+amp*k*k*Math.sin(w*n*dt-k*r3)/r3;
}
s++;
}
}
}
}
DrawCanvas.java :
//DrawCanvas.java
/************************************************************************
各種グラフを描くための DrawCanvas クラス
DrawCanvas.class :
Last update : Feb. 3, 2006.
All rights reserved, Copyright (C) 2002-2006, Kiyoshi Minemura
modified by ISSHY : Oct. 23, 2011. revised on July 5, 2020
************************************************************************/
import java.awt.Canvas;
import java.awt.Color;
import java.awt.Graphics;
import java.awt.Image;
class DrawCanvas extends Canvas{
private Graphics g;
private Image img;
private int Width, Height; // HTML から取得したウィンドウのサイズ
private int Nup, Nbot, Nxmin, Nymin;
private double xmin, xmax, ymin, ymax, rx, ry;
private double xorig=0.0,yorig=0.0;
// コンストラクタ
public DrawCanvas( Image im, Graphics bg, int width, int height ){
img = im; g = bg; Width = width; Height = height;
}
// ビューポート変換のための初期化メソッド
public void viewPort( int Nup, int Nbot, boolean aspect, double range){
// Nup,Nbot= 画面の上側、下側の非描画領域のサイズ（ピクセル値）
// aspect= 縦横比を正確に描く場合は true
// 対象とする図形の描画領域（ウィンドウポート）のサイズ
xmin = xorig-range; xmax = xorig+range; ymin = yorig-range; ymax = yorig+range;
//System.out.println("xmin="+xmin+", xmax="+xmax+", ymin="+ymin+" ymax="+ymax);
transView( Nup, Nbot, aspect );
}
// ビューポート変換メソッド
public void transView( int Nup, int Nbelow, boolean aspect ){
// Nup,Nbelow = ウィンドウ上下の非描画域寸法（ピクセル単位）
// aspect = 真偽値変数, アスペクト比を正しく表現する場合は "true"
double ap = ( ymax - ymin )/( xmax - xmin );
double aw = (double)( Height - Nup - Nbelow )/Width;
rx = Width/( xmax - xmin );
ry = 2*( Height - Nup - Nbelow )/( ymax - ymin );
Nxmin = 0; Nymin = Nbelow;
if( aspect == true ){
if( ap > aw ){
Nxmin = (int)( 0.5f*( 1.0f - ry/rx)*(double)Width );
rx = ry;
}else{
Nymin += (int)( 0.5*( 1.0f - rx/ry )*(double)Height );
ry = rx;
}
}
}
// ｘ座標変換メソッド
public int xtr( double x ){ // オーバーロードメソッド
return (int)( rx*( x -xmin )) + Nxmin;
}
// ｙ座標変換メソッド
public int ytr( double y ){ // オーバーロードメソッド
return Height - Nymin - (int)( rx*( y - ymin ) );
}
// 変数 ｚ[] の最小値を求めるメソッド
public double Zmin( double z[] ){
double zmin = z[0];
for( int k = 1; k < z.length; k++){
if( zmin > z[k] ) zmin = z[k];
}
return zmin;
}
// 変数 ｚ[] の最大値を求めるメソッド
public double Zmax( double z[] ){
double zmax = z[0];
for( int k = 1; k < z.length; k++){
if( zmax < z[k] ) zmax = z[k];
}
return zmax;
}
// ３角形格子の節点番号を付けるメソッド
public void gridNum( int N, int M, int E[][]){
int k = 0;
for( int j = 0; j < N-1; j++){
for( int i = 0; i < M-1; i++){
E[k][0] = M*i + j; E[k][1] = M*i + j + M;
E[k][2] = M*i + j + 1;
k++;
E[k][0] = M*i + j + 1; E[k][1] = M*i + j + M;
E[k][2] = M*i + j + M + 1;
k++;
}
}
}
// =======================================================================
// 簡易ペインタ法により曲面を網目状に描くメソッド
// revised by ISSHY
public void simPaint(double x[],double y[],double z[],double theta,double psi,int N,int M,int E[][],int flag){
// N×M 個の3次元データ(x,y,z) で、ｚ は高さに相当
double ax [] = new double [3], ay [] = new double[3], az [] = new double [3];
int X [] = new int [3], Y [] = new int[3], Z [] = new int [3];
int k = 0, n;
int k0, k1, k2, k3;
// 軸測投影図を描くデータための図形回転角度
double ct = Math.cos( theta ), st = Math.sin( theta );
double cp = Math.cos( psi ), sp = Math.sin( psi );
double zm;
//double zmax = Zmax( z ), zmin = Zmin( z );
float Hcol, Scol=1.0f, Bcol = 1.0f;
int Xmin,Xmax,Ymin,Ymax;
double lxmax=1.3f*(xmax+xorig),lxmin=1.3f*(xmin+xorig);
double lymax=1.3f*(ymax+yorig),lymin=1.3f*(ymin+yorig);
//System.out.println("lxmin="+lxmin+", lxmax="+lxmax+", lymin="+lymin+" lymax="+lymax);
Xmin=xtr(lxmin*st); Xmax=xtr(lxmax*st);
Ymin=ytr(-lymin*sp*ct); Ymax=ytr(-lymax*sp*ct);
g.setColor(Color.black);
g.drawLine(Xmin, Ymin, Xmax, Ymax);
g.drawString("X", Xmax, Ymax);g.drawString("-X", Xmin, Ymin);
Xmin=xtr(lxmin*ct); Xmax=xtr(lxmax*ct);
Ymin=ytr(lymin*sp*st); Ymax=ytr(lymax*sp*st);
g.drawLine(Xmin,Ymin,Xmax,Ymax);
g.drawString("Y", Xmax, Ymax);g.drawString("-Y", Xmin, Ymin);
for( int j = N-2; j >= 0; j--){
for( int i = M-2; i >= 0; i--){
k = 2*( N - 1 )*j + 2*i + 1;
k0 = M*i + j; k1 = k0 + M; k2 = k1 + 1;
zm = ( z[k0] + z[k1] + z[k2])/3.0;
Hcol=-1.5f*(float)(zm-1.0);
for( int repeat = 0; repeat < 2; repeat++){
if( repeat == 1 ) k -= 1;
for( int m = 0; m < 3; m++){
n = E[k][m];
ay[m] = st*x[n] + ct*y[n];
az[m] = -sp*ct*x[n] + sp*st*y[n] + cp*z[n];
}
if( S_norm( ay, az ) == true ){
// visible when S_norm >= 0 ( = "true" )
for( int m = 0; m < 3; m++ ){
X[m] = xtr( ay[m] ); Y[m] = ytr( az[m] );
}
if(flag==0){ // 単色で編目状に表示
g.setColor(Color.white);
g.fillPolygon(X,Y,3); // 背景色で塗りつぶし
g.setColor(Color.black);
g.drawPolygon(X,Y,3); // 手前側の線の描き直し
}else{ // カラーでの面塗り
g.setColor(Color.getHSBColor( Hcol, Scol, Bcol ) );
g.fillPolygon( X, Y, 3 );
g.setColor(Color.black);
g.drawPolygon(X,Y,3);
}
}
}
}
}
}
// 面の法線ベクトルを計算するメソッド
public boolean S_norm( double y[], double z[] ){
// (y, z) = 面を外側から見て反時計周りに番号付けした順に並べた座標値
// 面の法線と視点方向へのベクトル内積を求め、可視の場合は true を返す
double aa = ( y[1] - y[0] )*( z[2] - z[0] )-( y[2] - y[0] )*( z[1] - z[0] );
if( aa > 0.0 ) return true; else return false;
}
// ==============================================================
// アクセスメソッド
public Image getImage(){ return img; }
public void deleteImage(){ g.clearRect( 0, 0, Width, Height ); }
}
