複素積分の公式について

$$
第5章及び第6章の議論を理解するための数学的準備として, 有馬・神部：「複素関数論」の § 9.2 「積分の主値および佐藤の超関数」(p.109 $\sim$) からの抜粋を記しておく．

---

次の実軸上の積分 $I$ の評価を考える．まず $x$ を複素変数 $z$ に置き換えて, 被積分関数を複素平面に解析接続した関数 $F(z)$ を定義する：

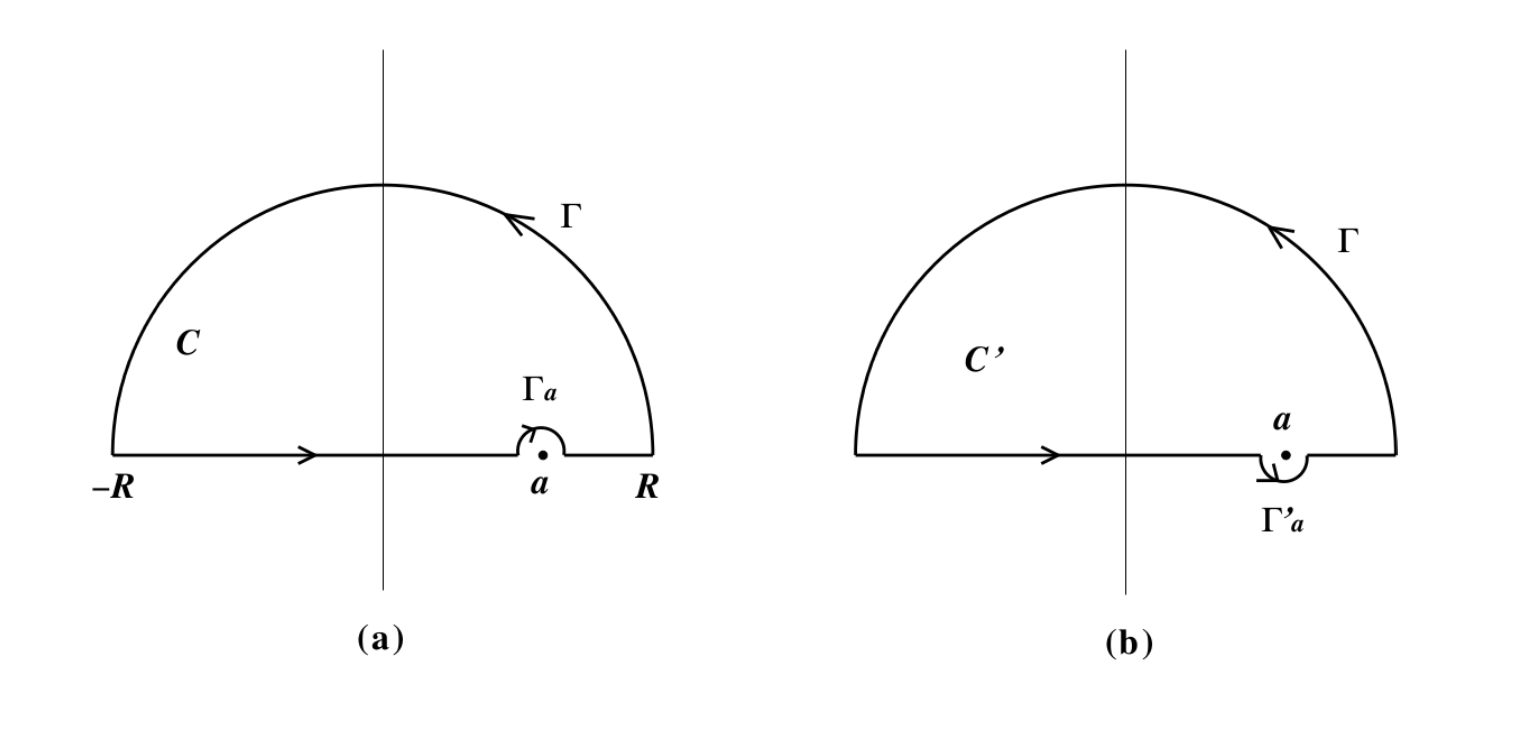
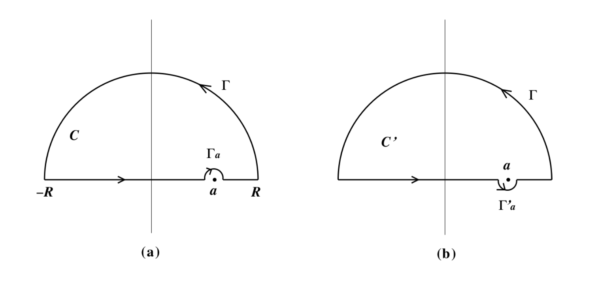
ただし, 分子の関数 $f(z)$ は $z=a$ のみならず実軸上で正則であるとし, また $|z{|}^k|f(z)|$ は有界であるとする．関数 $F(z)$ は点 $a$ に一位の極を持っている．そこで下図 1. の　(a)のような極 $a$ の上方を迂回する実軸に沿う経路と十分大きな半径 $R$ の上半面 $\mathrm{\Gamma }$ 上の閉曲線 $C$ 上の積分を考える． $a$ を迂回する曲線は半径 $\epsilon$ の半円 ${\mathrm{\Gamma }}_a$ とする．このとき,「留数の定理」より次が言える：

このとき最後の項は $R\to \mathrm{\infty }$ のとき無限小となるので無視できる．また第3項は $\epsilon \to 0$ のとき $z-a=\epsilon e^{i\theta }$ とおくと $dz=i\epsilon e^{i\theta }d\theta$ なので次となる：

ここで, 次の量を「コーシーの積分主値 (principal value)」と呼ぶ：

以上のことから, 式(2)は $R\to \mathrm{\infty }$， $\epsilon \to 0$ の極限で次に書けることが分かる：

次に, 点 $a$ の迂回の仕方を変えて上図 1. の (b) のようにしてみる．今度の閉曲線 $C^{\prime }$ についての積分は, 式 (3) に対応する値は $i\pi f(a)$ になるので次となる：

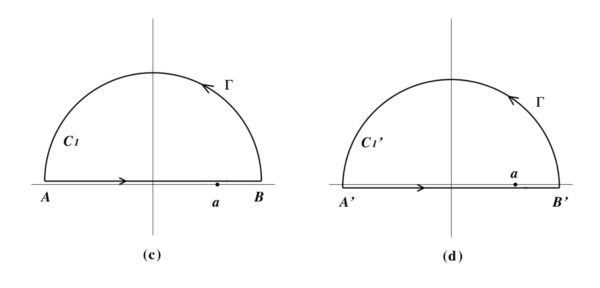
積分経路の取り方を少し変えて, 実軸から少し上または下にずらしてみる．即ち, 上図 1. の代わりに 下図 2. (a) のように $AB$ の部分は $z=x+i\epsilon$ としてみる． $\epsilon$ を十分小さく取り, 実軸と $AB$ の間には $f(z)$ の特異点は含まれないとすれば， 2つの閉曲線 $C$ と $C_1$ に関する積分は一致する．従って次の等式が得られる：

同様に, 直線部分を下にずらして, 図 (d)のように区間 $A^{\prime }{B}^{\prime }$ を $z=x-i\epsilon$ として積分しても， $C^{\prime }$ と $C_1^{\prime }$ に関する積分は不変であろう．従って, 次に書ける：

$$\begin{array}{}\text{(8)}& \underset{\epsilon \to +0}{lim}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{f(x)}{x-a-i\epsilon }dx=\mathrm{P}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{f(x)}{x-a}dx+i\pi f(a)\end{array}$$

この式は, 第6章の式 (6-109) を導出する際に利用することが出来る．

上記の積分関係は, 記号的に次のように書かれることがある：

この両辺に $f(x)$ を掛けて, 区間 $(-\mathrm{\infty },\mathrm{\infty })$ で積分すれば上の両式が得られるという意味である：

式 (9) において $a=0$ としてから全体に $i$ を掛け合わせ $x\Rightarrow \omega$ と記した場合が, 第5章の式 (5-17) である：

$$\begin{array}{}\text{(5-17)}& \underset{\epsilon \to +0}{lim}\frac{i}{\omega +i\epsilon }=\mathrm{P}\frac{i}{\omega }d\omega +\pi \delta (\omega )\end{array}$$

上式 (5-17) は「ヘビサイドの単位関数 (Heaviside unit function)」または「単位階段関数(unit step function)」： $u(t)$ のフーリエ変換と見做すことも出来る事に注意するべし：

その詳しい議論は, 例えば H.P.スウ：「フーリエ解析」の § 5.4 を参照すべし．